CD71.【C++ Dev】二叉樹的三種非遞歸遍歷方式

1.知識回顧

2.前序遍歷

分析

總結入棧的幾種可能

循環的條件

代碼

提交結果

3.中序遍歷

分析

代碼

提交結果

3.★后序遍歷

分析

問題:如何確定是第一次訪問到棧的元素還是第二次訪問到棧中的元素?

方法1:使用填充的內存(依賴于架構)

判斷計算機使用的架構和指針大小

代碼

提交結果

方法2:尋找規律,設置一個prev變量記錄上一個訪問的節點

代碼

運行結果

方法3:使用標記棧

代碼

運行結果

1.知識回顧

106.【C語言】數據結構之二叉樹的三種遞歸遍歷方式

L17.【LeetCode題解】前序遍歷

L18.【LeetCode題解】中序遍歷和后序遍歷

2.前序遍歷

https://leetcode.cn/problems/binary-tree-preorder-traversal/

給你二叉樹的根節點 root ，返回它節點值的?前序?遍歷。

示例 1：

輸入：root = [1,null,2,3]

輸出：[1,2,3]

解釋：

示例 2：

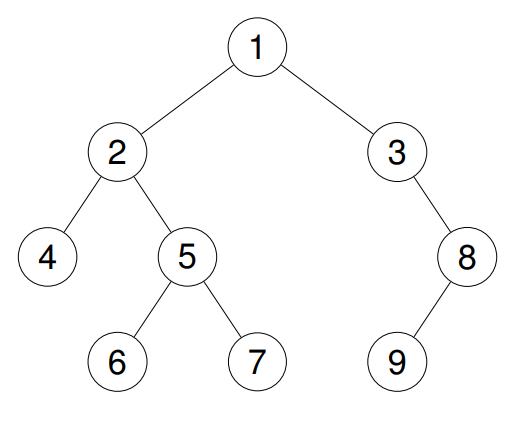
輸入：root = [1,2,3,4,5,null,8,null,null,6,7,9]

輸出：[1,2,4,5,6,7,3,8,9]

解釋：

示例 3：

輸入：root = []

輸出：[]

示例 4：

輸入：root = [1]

輸出：[1]

提示：

樹中節點數目在范圍 [0, 100] 內
-100 <= Node.val <= 100

進階：遞歸算法很簡單，你可以通過迭代算法完成嗎？

分析

以這棵樹[8,3,10,1,6,null,null,null,null,4,7]為例分析:

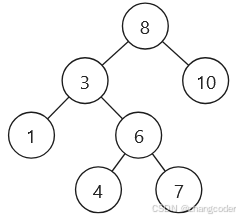
前序遍歷必然最先訪問左路節點,其次是左路節點的右子樹,需要一直重復這個過程

那么可以分成兩部分:

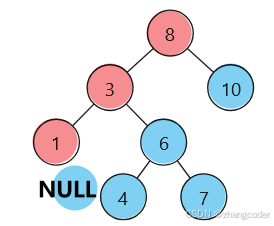
(紅色是左路節點,藍色是左路節點的右子樹)

訪問順序:8→3→1→1的右子樹→3的右子樹→8的右子樹

會發現:記錄8→3→1遍歷順序又要訪問1、3、8的右子樹(恰好是8、3、1倒過來的順序)

可以利用棧:先訪問左路節點(左路節點入前序遍歷數組),后左路節點入棧(入棧的是節點的指針),訪問左路節點的右子樹需要使用棧頂元素,彈出的節點記錄到前序遍歷的數組中,而且需要使用一個指針cur從根節點開始遍歷樹

1. cur指向一個節點意味著訪問一棵樹的開始
2. 棧里面的節點意味著要訪問它的右子樹

樹分成左路節點和右子樹右子樹再分成左路節點和右子樹右子樹再再分成左路節點和右子樹……

先入左節點:

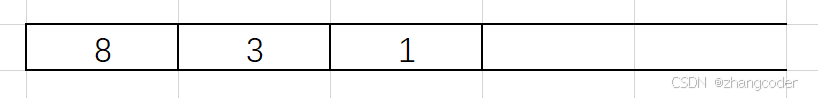
1的左子樹為空,需要彈出棧頂元素,訪問右節點

訪問右子樹前要先彈出左子樹的所有節點:

1的左和右子樹為NULL,直接彈出:

3的右子樹不為NULL,彈出3后入右子樹:

6的左子樹為4,繼續入棧:

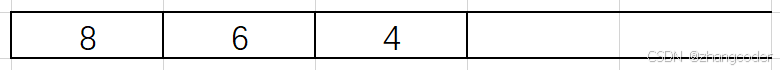
4的左和右子樹節點為NULL,直接彈出:

6的右子樹不為NULL,彈出6后入右子樹:

7的左和右子樹節點為NULL,直接彈出:

8的右子樹不為NULL,彈出8后入右子樹:

10的左和右子樹節點為NULL,直接彈出:

棧為空,循環結束

總結入棧的幾種可能

1.棧頂的左右子樹都為空,直接彈出

2.棧頂的左子樹不為空,將左子樹入棧

3.棧頂的右子樹不為空,彈出棧頂后,將右子樹入棧

//必然最先訪問左路節點
while(cur)
{st.push(cur);cur=cur->left;
}//左路節點的右子樹,需要取棧頂元素
auto elem=st.top();
st.pop();
ret.push_back(elem->val);
cur=elem->right;//子問題的方式訪問右子樹

循環的條件

顯然棧不為空就繼續循環,但如果只寫這個條件會導致有些測試用例過不了

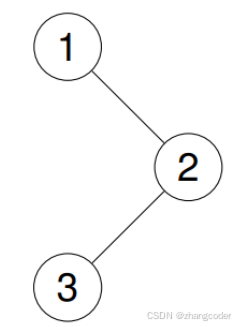
原因是1的左子樹為空,將1出棧后,恰滿足棧為空的循環退出條件,導致2和3沒有訪問到,需要添加cur如果不為空,也可以繼續循環

而且"cur不為空"這個條件應該比"棧不為空"這個條件先判斷,可以使用短路運算的規則:

while (cur || ! !st.empty())
{//......
}

代碼

class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {if (root==nullptr)return {};vector<int> ret;stack<TreeNode*> st;TreeNode* cur=root;while (cur || !st.empty()){//必然最先訪問左路節點while(cur){st.push(cur);ret.push_back(cur->val);cur=cur->left;}//訪問左路節點的右子樹,需要取棧頂元素auto elem=st.top();st.pop();cur=elem->right;// 子問題的方式訪問右子樹} return ret;}
};

提交結果

3.中序遍歷

https://leetcode.cn/problems/binary-tree-inorder-traversal/

給定一個二叉樹的根節點 root ，返回 它的中序?遍歷 。

示例 1：
輸入：root = [1,null,2,3]
輸出：[1,3,2]
示例 2：
輸入：root = []
輸出：[]
示例 3：
輸入：root = [1]
輸出：[1]
提示：

樹中節點數目在范圍 [0, 100] 內
-100 <= Node.val <= 100

進階:?遞歸算法很簡單，你可以通過迭代算法完成嗎？

分析

中序遍歷:左→根→右,即左子樹訪問完了才能訪問根和右子樹

反復執行這兩步:

1. 左路節點入棧
2. 訪問左路節點及左路節點的右子樹

????????從棧里面取到一個節點(pop)就意味這個節點左子樹已經訪問完了

稍微改改前序遍歷的代碼即可

代碼

class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {if (root==nullptr)return {};vector<int> ret;stack<TreeNode*> st;TreeNode* cur=root;while (cur || !st.empty()){//先遍歷左子樹,但不訪問其中的節點,即不要push_back到ret中while(cur){st.push(cur);cur=cur->left;}//左子樹遍歷完了,那就訪問根和右子樹auto elem=st.top();st.pop();ret.push_back(elem->val);cur=elem->right;// 子問題的方式訪問右子樹} return ret;}
};

提交結果

3.★后序遍歷

https://leetcode.cn/problems/binary-tree-postorder-traversal/

給你一棵二叉樹的根節點 root ，返回其節點值的 后序遍歷 。

示例 1：

輸入：root = [1,null,2,3]

輸出：[3,2,1]

解釋：

示例 2：

輸入：root = [1,2,3,4,5,null,8,null,null,6,7,9]

輸出：[4,6,7,5,2,9,8,3,1]

解釋：

示例 3：

輸入：root = []

輸出：[]

示例 4：

輸入：root = [1]

輸出：[1]

提示：

樹中節點的數目在范圍 [0, 100] 內
-100 <= Node.val <= 100

進階：遞歸算法很簡單，你可以通過迭代算法完成嗎？

分析

后序遍歷:左→右→根,即必須訪問完左子樹和右子樹才能訪問根

以這棵樹[8,3,10,1,6]為例分析:

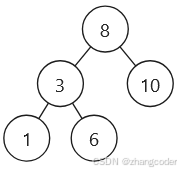
仍然分成兩部分:

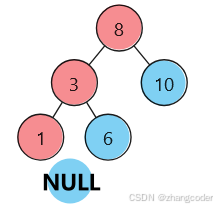
(紅色是左路節點,藍色是左路節點的右子樹)

左路節點入棧:

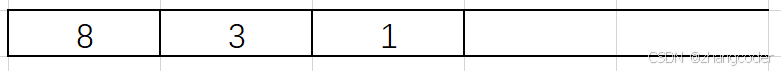
1的左和右子樹為NULL,直接彈出1,將1記錄到后序遍歷的數組中:

雖然3的右子樹不為空,但是不能彈出3,如果彈出3那就成前序遍歷了,應該等第二次訪問到棧里面的3才彈出3(即將3的左右子樹都訪問完才能訪問根節點3)

入3的右子樹

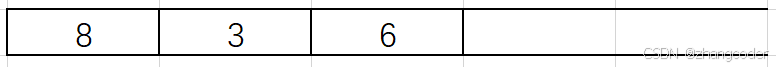
6的左和右子樹為NULL,直接彈出6,將6記錄到后序遍歷的數組中:

第二次遇到3,因為3的左右子樹都訪問完了,可以彈出3,將3記錄到后序遍歷的數組中:

雖然8的右子樹不為空,但是不能彈出8(理由見上),入8的右子樹:

10的左和右子樹為NULL,直接彈出10,將10記錄到后序遍歷的數組中:

第二次遇到8,因為8的左右子樹都訪問完了,可以彈出8,將8記錄到后序遍歷的數組中:

棧為空,循環結束

問題:如何確定是第一次訪問到棧的元素還是第二次訪問到棧中的元素?

上面提到了:"雖然3的右子樹不為空,但是不能彈出3,如果彈出3那就成前序遍歷了,應該等第二次訪問到棧里面的3才彈出3(即將3的左右子樹都訪問完才能訪問根節點3)"

方法1:使用填充的內存(依賴于架構)

得知題目條件"樹中節點的數目在范圍 [-100, 100] 內",而且TreeNode的val是用int存儲的,如果val>0,那么最多只會占用int的低7位,如果val<0,那么int所有位都會占用

顯然在val內部使用一個標志位來判斷是第一次訪問到棧的元素還是第二次訪問到棧中的元素是不切實際的

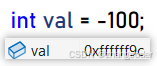
突破口:結構體的內存對齊

64位下,TreeNode結構體的內存分布圖:

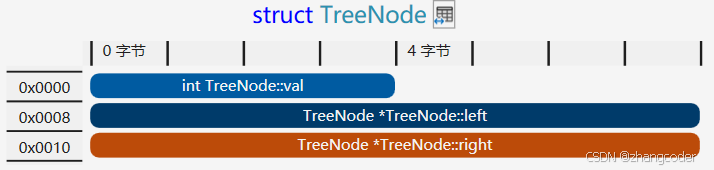
會發現0x0004~0x007是填充的4個字節,沒有用處!

填充的字節可以借用其中一個字節來標記是第一次還是第二次訪問到棧中的元素,簡稱為標志字節

例如選這一字節:

怎么從標志字節哪里得知是第一次還是第二次訪問到棧中的元素呢?

對于填充的字節,編譯器會給初始值,LeetCode下的值是0xBE,Windows VS2022下的值是0xCD,下面padding_byte獲取到的就是初始字節(pad v.填充)

unsigned char padding_byte = *((unsigned char*)&(root->val) + 4);

那么第一次訪問過節點后可以設置標志字節為指定值,讓其不等于原來編譯器給的初始值就行了,例如可以設置成0x01,等到第二次訪問發現是0x01,就能讓棧頂元素出棧,寫入到后序遍歷的數組中

如果LeetCode是64位架構且沒有使用gcc的-m32選項,那么上述方法是可行的,可以用宏判斷:

判斷計算機使用的架構和指針大小

#if defined(__x86_64__) || defined(_M_X64)printf("This is a 64-bit x86 architecture\n");
#elif defined(__i386__)printf("This is a 32-bit x86 architecture\n");
#elif defined(__arm__) || defined(_M_ARM)printf("This is an ARM architecture\n");
#elif defined(__aarch64__) || defined(_M_AARCH64)printf("This is a 64-bit ARM architecture\n");
#elseprintf("Unknown architecture\n");
#endif//__SIZEOF_POINTER__是指針大小
if (__SIZEOF_POINTER__ == 4) 
{printf("This is a 32-bit architecture.\n");
} 
else if (__SIZEOF_POINTER__ == 8) 
{   printf("This is a 64-bit architecture.\n"); 
} 
else 
{printf("Unknown architecture.\n");
}

LeetCode輸出結果:

使用填充的內存的方法是可行的

代碼

class Solution {
public:vector<int> postorderTraversal(TreeNode* root){if (root == nullptr)return {};vector<int> ret;unsigned char padding_byte=*((unsigned char*)&(root->val)+4);stack<TreeNode*> st;TreeNode* cur = root;while (cur || !st.empty()){//先遍歷左子樹,但不訪問其中的節點,即不要push_back到ret中while (cur){st.push(cur);cur = cur->left;}//左子樹遍歷完了,那就訪問根和右子樹auto elem = st.top();unsigned char* flag_byte_ptr=(unsigned char*)&(elem->val)+4;if (elem->right == nullptr){ret.push_back(elem->val);st.pop();continue;}if (*flag_byte_ptr!=padding_byte){//第二次訪問到,說明左右子樹都訪問完了,必須重新設置curst.pop();ret.push_back(elem->val);continue;}else{//第一次訪問到,要設置標志字節*flag_byte_ptr=1;}cur = elem->right;// 子問題的方式訪問右子樹}return ret;}
};

提交結果

方法2:尋找規律,設置一個prev變量記錄上一個訪問的節點

訪問右子樹有兩種情況:右為空(不用管右直接拿出棧頂元素),右不為空(需要使用上一次訪問的節點)

例如下圖的節點的3會訪問到兩次:

由方法1的棧圖分析

1.如果3的右子樹沒有訪問過,上一次訪問的是3的左子樹的根1

↓?

2..如果3的右子樹訪問過,上一次訪問的是3的右子樹的根6

↓?

設置一個變量prev記錄cur訪問的前一個節點即可

代碼

class Solution {
public:vector<int> postorderTraversal(TreeNode* root){if (root == nullptr)return {};vector<int> ret;stack<TreeNode*> st;TreeNode* cur = root;TreeNode* prev = nullptr;while (cur || !st.empty()){//先遍歷左子樹,但不訪問其中的節點,即不要push_back到ret中while (cur){st.push(cur);cur = cur->left;}//左子樹遍歷完了,那就訪問根和右子樹auto elem = st.top();if (elem->right == nullptr){prev=elem;ret.push_back(elem->val);st.pop();}if (prev==elem->right){//第二次訪問到,說明左右子樹都訪問完了,必須重新設置curprev=elem;st.pop();ret.push_back(elem->val);}else//prev=cur->left{cur = elem->right;// 第一次訪問到,子問題的方式訪問右子樹}   }return ret;}
};

運行結果

方法3:使用標記棧

標記棧的作用是標記對應的節點有沒有訪問過,是否訪問過這個節點就看標記棧的棧頂值

代碼

class Solution {
public:vector<int> postorderTraversal(TreeNode* root){if (root == nullptr)return {};vector<int> ret;stack<TreeNode*> st;stack<TreeNode*> flag;TreeNode* cur = root;while (cur || !st.empty()){//先遍歷左子樹,但不訪問其中的節點,即不要push_back到ret中while (cur){st.push(cur);cur = cur->left;}//左子樹遍歷完了,那就訪問根和右子樹auto elem = st.top();if (elem->right == nullptr){ret.push_back(elem->val);st.pop();continue;}if (flag.size()&&flag.top()==elem){//第二次訪問到,說明左右子樹都訪問完了,必須重新設置curst.pop();flag.pop();ret.push_back(elem->val);continue;}if (flag.empty() || flag.top()!=elem){//第一次訪問到,要設置標志字節flag.push(elem);}cur = elem->right;// 子問題的方式訪問右子樹}return ret;}
};