記錄一下今天完成的算法題,雖然這個難度是困難,但感覺沒有那個560.和為k的子數組和難想,這個題主要就前期遇到個優先隊列,因為之前沒用過,不太熟悉,剩下的思路感覺都屬于正常難度
問題描述

原始思路:優先隊列(最大堆)
原始代碼使用最大堆(PriorityQueue)存儲元素值及其索引,堆頂始終是當前窗口的最大值。但原始代碼存在邏輯錯誤,修正后的代碼如下:
import java.util.PriorityQueue;public class Solution {public int[] maxSlidingWindow(int[] nums, int k) {if (nums.length == 0) return new int[0];PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> b[0] - a[0]); // 最大堆// 初始化第一個窗口for (int i = 0; i < k; i++) {pq.offer(new int[]{nums[i], i});}int[] result = new int[nums.length - k + 1];result[0] = pq.peek()[0]; // 第一個窗口的最大值// 滑動窗口for (int i = k; i < nums.length; i++) {pq.offer(new int[]{nums[i], i}); // 1. 加入新元素while (pq.peek()[1] < i - k + 1) { // 2. 彈出不在窗口內的元素pq.poll();}result[i - k + 1] = pq.peek()[0]; // 3. 記錄當前窗口最大值}return result;}
}核心邏輯
- 初始化堆:將第一個窗口的元素?
[值, 索引]?加入最大堆。 - 滑動窗口:
- 加入新元素:將窗口右側新元素加入堆。
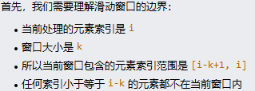
- 清理無效元素:彈出堆頂所有索引小于?
i - k + 1?的元素(這些元素已離開窗口)。 - 記錄最大值:堆頂元素即為當前窗口最大值。
復雜度分析
- 時間復雜度:
O(n log n)?每個元素入堆和出堆需?O(log n),最壞情況下(如單調遞增數組)堆中元素累積至?O(n)。 - 空間復雜度:
O(n)
缺陷
- 無效元素積累:堆中可能保留大量已離開窗口的元素,導致堆操作效率降低。
在此之上,我們延續優先隊列的思路,對代碼進行一下優化
優化方案1:單調隊列(雙端隊列)
使用雙端隊列(Deque)維護一個嚴格遞減的序列,隊首始終是當前窗口最大值。時間復雜度優化至 O(n)。
import java.util.Deque;
import java.util.LinkedList;public class Solution {public int[] maxSlidingWindow(int[] nums, int k) {if (nums.length == 0) return new int[0];Deque<Integer> deque = new LinkedList<>(); // 存儲索引int[] result = new int[nums.length - k + 1];for (int i = 0; i < nums.length; i++) {// 1. 清理超出窗口的隊首元素while (!deque.isEmpty() && deque.peekFirst() < i - k + 1) {deque.pollFirst();}// 2. 從隊尾移除小于當前元素的索引while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {deque.pollLast();}deque.offerLast(i); // 3. 當前索引入隊// 4. 記錄窗口最大值(從第k-1個元素開始)if (i >= k - 1) {result[i - k + 1] = nums[deque.peekFirst()];}}return result;}
}核心改進
- 嚴格遞減隊列:?每次添加新元素時,從隊尾移除所有小于它的元素索引,確保隊列嚴格遞減。
- 隊首即最大值:?隊首對應元素始終為當前窗口最大值。
- 即時清理無效元素:?在添加新元素前,先清理離開窗口的隊首元素,避免無效積累。
復雜度分析
- 時間復雜度:
O(n)?每個元素最多入隊和出隊一次。 - 空間復雜度:
O(k)?隊列最多存儲?k?個元素。
優化方案2:分塊預處理(空間換時間)
將數組分成大小為 k 的塊,預處理每個塊的 前綴最大值 和 后綴最大值,利用二者快速計算窗口最大值。
public class Solution {public int[] maxSlidingWindow(int[] nums, int k) {if (nums.length == 0) return new int[0];int n = nums.length;int[] prefixMax = new int[n];int[] suffixMax = new int[n];// 計算前綴最大值for (int i = 0; i < n; i++) {prefixMax[i] = (i % k == 0) ? nums[i] : Math.max(prefixMax[i - 1], nums[i]);}// 計算后綴最大值suffixMax[n - 1] = nums[n - 1];for (int i = n - 2; i >= 0; i--) {suffixMax[i] = ((i + 1) % k == 0) ? nums[i] : Math.max(suffixMax[i + 1], nums[i]);}// 計算每個窗口最大值int[] result = new int[n - k + 1];for (int i = 0; i <= n - k; i++) {result[i] = Math.max(suffixMax[i], prefixMax[i + k - 1]);}return result;}
}核心邏輯
- 前綴最大值:?
prefixMax[i]?= 從塊起點到?i?的最大值。 - 后綴最大值:?
suffixMax[i]?= 從?i?到塊終點的最大值。 - 窗口最大值:?設窗口為?
[i, j](j = i + k - 1),則最大值 =?max(suffixMax[i], prefixMax[j])。
復雜度分析
- 時間復雜度:
O(n)?預處理和計算結果各需遍歷一次數組。 - 空間復雜度:
O(n)?需額外存儲前綴和后綴最大值數組。
總結
| 方法 | 時間復雜度 | 空間復雜度 | 核心優勢 |
|---|---|---|---|
| 優先隊列(修正) | O(n log n) | O(n) | 邏輯簡單,易實現 |
| 單調隊列 | O(n) | O(k) | 最優效率,推薦使用 |
| 分塊預處理 | O(n) | O(n) | 無隊列操作,適合并行計算 |
推薦實現:單調隊列法在性能和代碼簡潔性上達到最佳平衡,是解決滑動窗口最大值問題的首選方案。

)
)



)
:靜態路由、動態路由、默認路由)











 —— 致力于建立第一個圖像分割基礎模型)