吳恩達深度學習筆記

最近在看吳恩達深度學習系列課程，簡單做一個基本框架筆記。
如感興趣或了解更多內容，推薦看原課程
以前也做過一些與機器學習和深度學習有關的筆記，過分重復的就一筆帶過了。

01 第一門課神經網絡和深度學習

1.1 第一周：深度學習引言

略

1.2 第二周：神經網絡的編程基礎

需要基本了解：

二分類
邏輯回歸
邏輯函數的代價函數（理解為什么要有代價函數）
梯度下降法（參數如何更新）
導數（理解微積分即可）
計算圖（關于這個，“魚書”將很好很詳細，推薦，用來理解反向傳播很方便）
利用計算圖求導數（本質上就是求導的鏈式法則）
邏輯回歸中的梯度下降
m個樣本的梯度下降
向量化（是為了解決若采用for循環的慢速，向量化更高效，但要注意維度對應上）
python中的廣播（broadcasting）

1.3 第三周：淺層神經網絡

以兩層神經網絡為例，基本邏輯：

結構（包括輸入層，隱藏層，輸出層）
單個神經元的計算
多樣本的向量化
激活函數（常用種類，為什么要用非線性激活函數，激活函數的導數）
神經邏輯的梯度下降（與前面邏輯回歸的梯度下降的基本思路，基本一致）
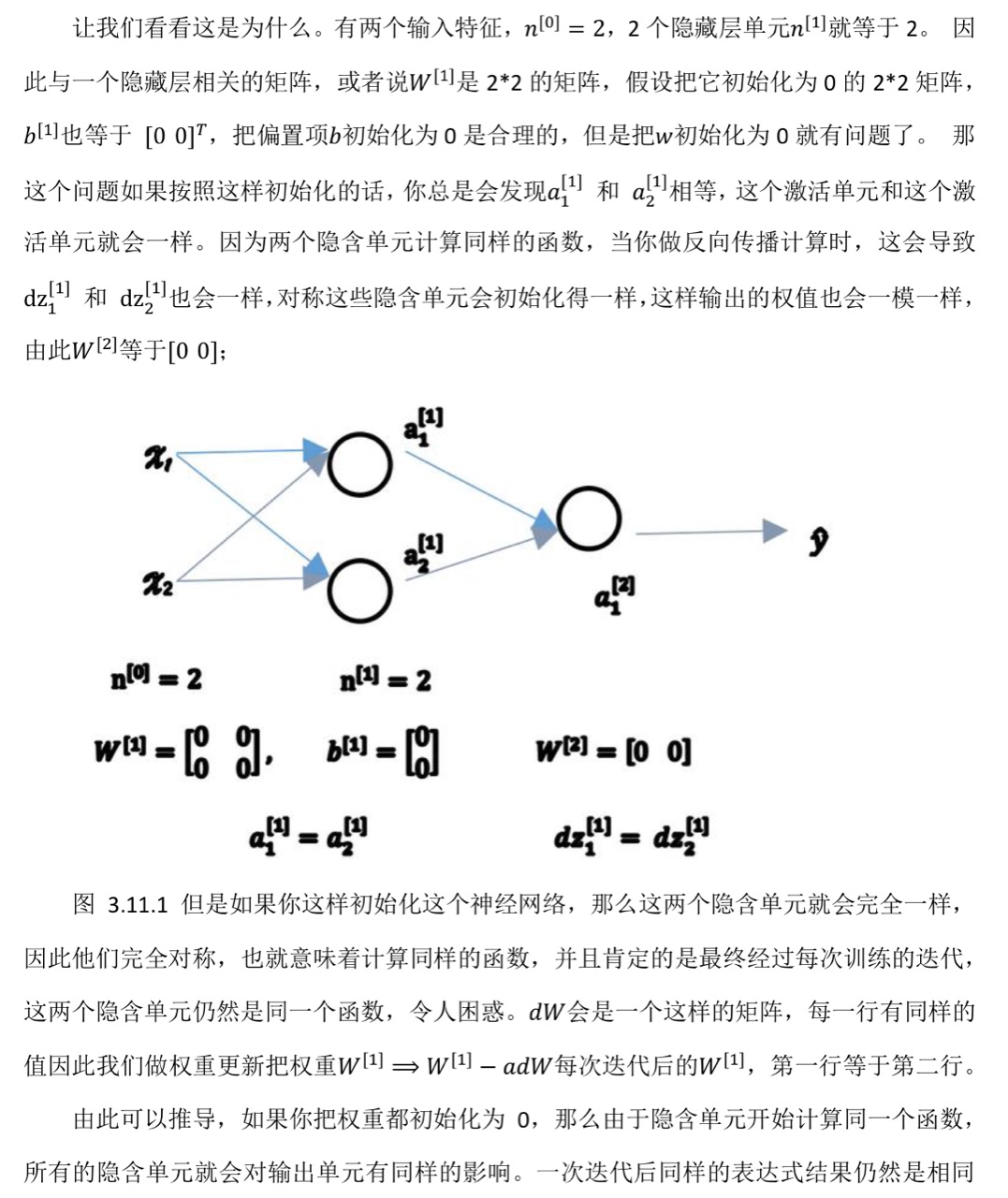
隨機初始化（對于一個神經網絡，把權重等參數都初始化為0，梯度下降將不會再起作用）

關于第六點的詳細解釋：

1.4 第四周：深層神經網絡

隱藏層的數量可看作一個可自由選擇大小的超參數
如果有比較多的隱藏層（網絡比較深），總體上能夠學更復雜的函數
前向傳播和后向傳播的基本邏輯，和淺層神經網絡一致

02 第二門課改善深層神經網絡：超參數調試，正則化以及優化

2.1 第一周：深度學習的實踐層面

2.1.1 訓練，驗證，測試集

先利用訓練集，執行算法進行訓練，通過驗證集或簡單交叉驗證集選擇最好的模型（比如超參數等的選擇）。
經過充分驗證，選定了最終模型，在測試集上進行評估。

在小數據量時代，常見做法是將所有數據三七分，即70%驗證集+30%測試集，如果沒有明確設置驗證集，也可以按照 60%訓練，20%驗證和 20%測試集來劃分。
在現在大數據階段，驗證集和測試集占數據總量的比例會趨向于變得更小。

2.1.2 偏差，方差

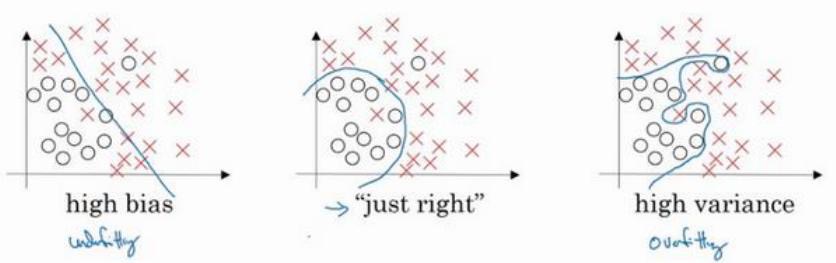
最左邊的圖片，用邏輯回歸進行擬合，并不能很好地擬合該數據，這是高偏差（high bias）的情況，稱為“欠擬合”（underfitting）。

最右邊的圖片，擬合方式分類器方差較高（high variance），數據過度擬合（overfitting）。

理解偏差和方差的兩個關鍵數據是訓練集誤差（Train set error）和驗證集誤差（Dev set error）

假定訓練集誤差是 1%，驗證集誤差是 11%，可以看出訓練集結果非常好，而驗證集結果相對較差。我們可能過度擬合了訓練集，泛化能力（適用于沒訓練的數據的結果較差）在某種程度上，驗證集并沒有充分利用交叉驗證集的作用，像這種情況稱為“高方差”。
假設訓練集誤差是 15%，驗證集誤差是 16%。且假設該案例中人的錯誤率幾乎為 0%。可得知，算法并沒有在訓練集中得到很好訓練，如果訓練數據的擬合度不高，就是數據欠擬合，就可以說這種算法偏差比較高。
假設訓練集誤差是 15%，驗證集的錯誤率達到 30%。在這種情況下，會認為這是方差偏差都很糟糕的情況。
如果訓練集誤差是 0.5%，驗證集誤差是 1%，則是很好的情況，偏差和方差都很低。

最優誤差也被稱為貝葉斯誤差。
如果最優誤差或貝葉斯誤差非常高，比如 15%。此時訓練誤差 15%，驗證誤差 16%，15%的錯誤率對訓練集來說也是非常合理的，偏差不高，方差也非常低。

需要根據實際情況（高偏差，還是高方差），采取不同的措施。

2.1.3 L2 正則化

前面提到了過擬合的問題—高方差。有兩個解決方法，一個是正則化，一個是準備更多的數據。

對w用L2正則化：

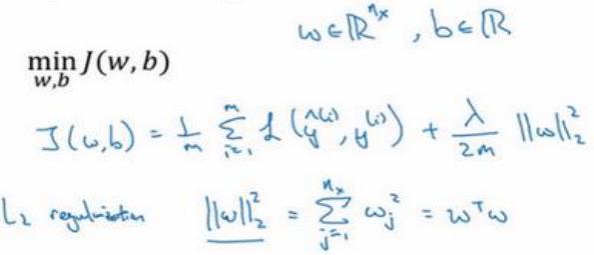
為什么一般對w用2范數？
因為w通常是一個高維參數向量，幾乎可以涵蓋所有參數。是否對b使用2范數的正則化，并不太影響最終結果。

L2正則化是最常見的正則化函數。

提問，為什么正則化有利于預防過擬合？
當處于過擬合狀態時，若正則化𝜆設置得足夠大，權重矩陣𝑊被設置為接近于 0 的值，直觀理解就是把多隱藏單元的權重設為 0，于是基本上消除了這些隱藏單元的許多影響。（0這里算時比較極端的假設）
𝜆會存在一個中間值，于是會有一個接近“Just Right”的中間狀態。

2.1.4 dropout 正則化

除了𝐿2正則化，還有一個非常實用的正則化方法——“Dropout（隨機失活）”.

假設我們需要訓練的神經網絡圖如下，存在過擬合現象：

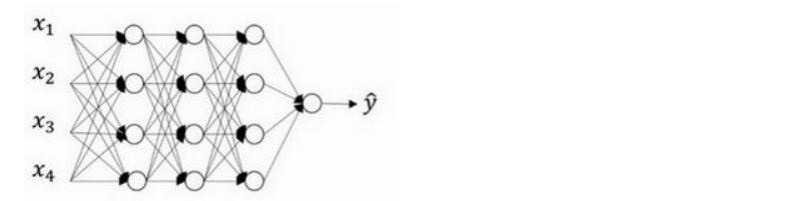
dropout 會遍歷網絡的每一層，并設置消除神經網絡中節點的概率
假設網絡中的每一層，設置每個節點得以保留和消除的概率都是 0.5。
設置完節點概率，我們會消除一些節點，然后刪除掉從該節點進出的連線，最后得到一個節點更少，規模更小的網絡。

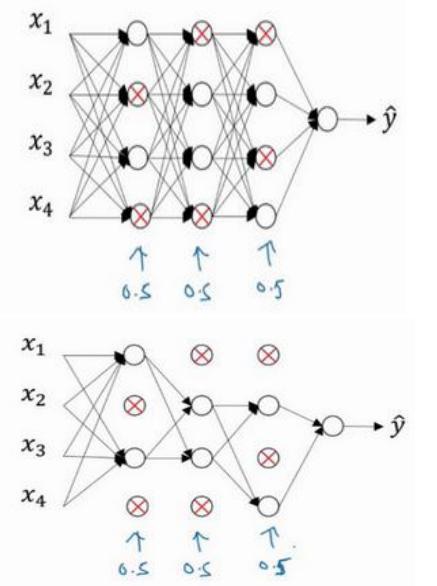
對于其他樣本，我們同樣這樣設置概率，保留一類節點集合，刪除其它類型的節點集合。
對于每個訓練樣本，我們都將采用一個精簡后神經網絡來訓練它。

如何實施 dropout 呢？
下面主要講inverted dropout（反向隨機失活）。
出于完整性考慮，用一個三層（𝑙 = 3）網絡來舉例說明。

首先要定義向量𝑑，𝑑[3]表示一個三層的 dropout 向量：
d3 = np.random.rand(a3.shape[0],a3.shape[1])
然后看它是否小于某數，我們稱之為 keep-prob，keep-prob 是一個具體數字。例如前面我們就設置的0.5。
接下來，從第三層中獲取激活函數，叫做𝑎[3]。使用 a3=np.multiply(a3,d3)，就可以利用乘法運算，得到相應元素的輸出。
最后，進行調整，使用a3/=keep-prob。
解釋原因：
50 個神經元，在一維上𝑎[3]是 50，我們通過因子分解將它拆分成50 × 𝑚維的。
假設保留和刪除它們的概率分別為 80%和 20%，這意味著最后被刪除或歸零的單元平均有 10（50×20%=10）個。
看𝑧[4]，𝑧[4] = 𝑤[4]𝑎[3] + 𝑏[4]，我們的預期是，𝑎[3]減少 20%，也就是說𝑎[3]中有 20%的元素被歸零，為了不影響𝑧[4]的期望值，我們需要用𝑤[4]𝑎[3]/0.8，它將會修正或彌補所需要的那20%，a[3]的期望不會變。

顯然在測試階段，我們并未使用 dropout。
因為在測試階段進行預測時，我們不期望輸出結果是隨機的，如果測試階段應用 dropout 函數，預測會受到干擾。

2.1.5 理解dropout

一種理解是：
不依賴于任何一個特征，因為該單元的輸入可能隨時被清除，因此該單元通過這種方式傳播下去，并為單元的四個輸入增加一點權重，通過傳播所有權重。
dropout將產生收縮權重的平方范數的效果，和之前講的𝐿2正則化類似；實施 dropout 的結果實它會壓縮權重，并完成一些預防過擬合的外層正則化；𝐿2對不同權重的衰減是不同的，它取決于激活函數倍增的大小。
（可粗略理解為：dropout特征都有可能被隨機清除，或者說該單元的輸入也都可能被隨機清除。機器不愿意把所有賭注都放在一個節點上，不愿意給任何一個輸入加上太多權重，因為它可能會被刪除，因此該單元將通過這種方式積極地傳播開，并為單元的四個輸入增加一點權重，通過傳播所有權重）

不擔心過擬合問題的，keep-prob 可以為 1。
過擬合問題比較嚴重的，keep-prob會需要小一點。

dropout的缺點是，代價函數J不再被明確定義，每次迭代，都會隨機移除一些節點。如果要再三檢查梯度下降的性能，很難進行復查。

2.1.6 其他正則化方法

除了𝐿2正則化和隨機失活（dropout）正則化，還有幾種方法可以減少神經網絡中的過擬合：

數據擴增
通過隨意翻轉和裁剪圖片等方式，我們可以增大數據集，額外生成假訓練數據。
和全新的，獨立的貓咪圖片數據相比，這些額外的假的數據無法包含像全新數據那么多的信息，但我們這么做基本沒有花費，代價幾乎為零，除了一些對抗性代價。
early stopping
術語early stopping表示提早停止訓練神經網絡（如驗證集誤差開始上升的位置）