leetcode-hot-100 (鏈表）

1. 相交鏈表

題目鏈接：相交鏈表
題目描述：給你兩個單鏈表的頭節點 headA 和 headB ，請你找出并返回兩個單鏈表相交的起始節點。如果兩個鏈表不存在相交節點，返回 null 。

解答：

其實這道題目我一開始沒太看懂題目給這個鏈表的定義是干啥用的，后面看了解析才知道為了讓我們知道這個鏈表是如何創建的，以及如何進行鏈表數據的訪問。

方法一：哈希集合

反正題目已經明確表示整個鏈式結構中沒有環，因此直接使用一個集合，然后遍歷鏈表A中的所有元素（鏈表B也可以），將鏈表A中的每個節點加入到哈希集合中去。然后遍歷鏈表B，查詢當前B中的結點元素是否在哈希集合中出現過。

  • 要是如果當前節點不在哈希集合中，則繼續遍歷下一個節點；
  • 如果當前節點在哈希集合中，則后面的節點都在哈希集合中，即從當前節點開始的所有節點都在兩個鏈表的相交部分，因此在鏈表 headB 中遍歷到的第一個在哈希集合中的節點就是兩個鏈表相交的節點，返回該節點。

如果鏈表 headB 中的所有節點都不在哈希集合中，則兩個鏈表不相交，返回 null。

因此代碼編寫如下（官方的代碼）：

class Solution {
public:ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {unordered_set<ListNode*> visited;ListNode* temp = headA;while (temp != nullptr) {visited.insert(temp);temp = temp->next;}temp = headB;while (temp != nullptr) {if (visited.count(temp)) {return temp;}temp = temp->next;}return nullptr;}
};

方法二：雙指針

方法一中用到了哈希集合，因此空間復雜度是 O ( m ) O(m) O(m)，雙指針方法就是將空間復雜度降至 O ( 1 ) O(1) O(1)

雙指針的解法如下：在這里插入圖片描述
上述官方的解法為啥是對的呢，可視化如下的圖進行解釋：
情況一：要是兩個鏈表相交，則假設指針 P A P_A PA? 從 p p p 出發，指針 P B P_B PB? 從 q q q 出發，則指針 P A P_A PA? 的運動軌跡如下圖紅色部分，指針 P B P_B PB? 的運動軌跡如下圖黃色部分，按照圖中所表示的長度，可以發現，要是 a = b a = b a=b 這，兩指針一定會在紅色點處相遇，這樣就找到了結果，要是 a ! = b a!=b a!=b 則兩指針還是在紅色點處相遇。因此，兩指針最多遍歷鏈表A和鏈表B即可判斷出最終的結果。
情況二：要是兩個鏈表不相交，則依舊可以遍歷鏈表A和鏈表B即可判斷出最終的結果。
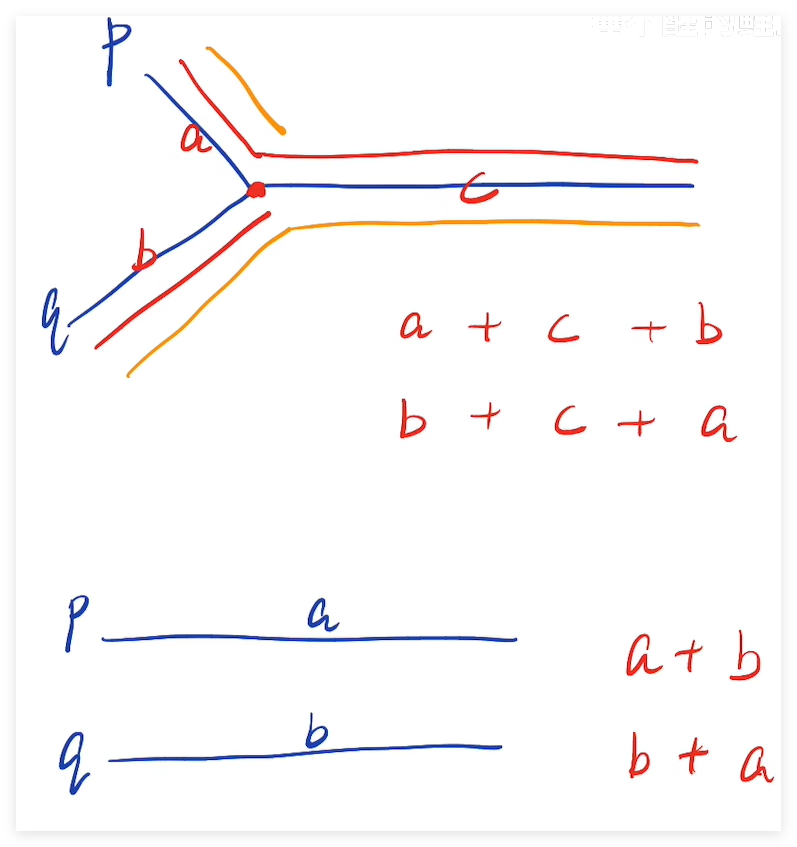
在這里插入圖片描述
因此這樣的話，時間復雜度就是兩鏈表的長度 O ( m + n ) O(m+n) O(m+n) ，空間復雜度就是常數級別的了 O ( 1 ) O(1) O(1)。
于是代碼編寫如下：

class Solution {
public:ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {if (headA == nullptr || headB == nullptr) {return nullptr;}ListNode *pA = headA, *pB = headB;while (pA != pB) {pA = pA == nullptr ? headB : pA->next;pB = pB == nullptr ? headA : pB->next;}return pA;}
};

2. 反轉鏈表

題目鏈接：反轉鏈表
題目描述：給你單鏈表的頭節點 head ，請你反轉鏈表，并返回反轉后的鏈表。

解答：

方法一：迭代法

示例：

輸入: 1 -> 2 -> 3 -> 4 -> 5
輸出: 5 -> 4 -> 3 -> 2 -> 1

使用三個指針進行鏈表的逐個反轉：

  • p：表示當前節點，逐步向后移動。
  • q：表示 p 的下一個節點，用于遍歷原始鏈表。
  • temp：臨時保存 q->next，防止鏈表斷裂。

在每一步中：

  1. 將 q->next 指向 p，實現局部反轉；
  2. 向后移動 p 和 q；
  3. 繼續處理直到 q == nullptr，即整個鏈表反轉完成；
  4. 最后將原頭節點指向 nullptr，避免循環引用；
  5. 返回新的頭節點 p。

C++ 實現代碼

class Solution {
public:ListNode* reverseList(ListNode* head) {if (!head || !head->next)return head;ListNode *p = head, *q = p->next, *temp = nullptr;while (q) {temp = q->next;   // 保存下一個節點q->next = p;      // 反轉當前節點的指針p = q;            // 移動 p 到當前節點q = temp;         // 移動 q 到下一個節點}head->next = nullptr; // 原頭節點現在是尾節點，指向空return p;             // 新的頭節點是 p}
};

時間與空間復雜度分析

  • 時間復雜度： O ( n ) O(n) O(n)，其中 n n n 是鏈表的長度。我們只需要遍歷一次鏈表。
  • 空間復雜度： O ( 1 ) O(1) O(1)，只使用了常數級別的額外空間。

示例解析

以鏈表 1 -> 2 -> 3 -> 4 -> 5 為例：

步驟pqtempq->nexthead->next
初始12--2
112312 → 1
223423 → 2 → 1
334534 → 3 → 2 → 1
445null45 → 4 → 3 → 2 → 1
結束5null--1 → null

最終返回 p = 5，鏈表成功反轉為：5 -> 4 -> 3 -> 2 -> 1

注意

  • 必須判斷邊界情況：if (!head || !head->next) return head;，處理空鏈表或只有一個節點的情況。
  • 不要忘記最后設置 head->next = nullptr，否則會導致循環鏈表或錯誤連接。

方法二：遞歸

我覺得遞歸主要還是不是很好想，但是代碼還是很簡潔的，具體的解釋見：
官方解答

class Solution {
public:ListNode* reverseList(ListNode* head) {if (!head || !head->next) {return head;}ListNode* newnode = reverseList(head->next);head->next->next = head;head->next = nullptr;return newnode;}
};

3. 回文鏈表

題目鏈接：回文鏈表
題目描述：給你一個單鏈表的頭節點 head ，請你判斷該鏈表是否為回文鏈表。如果是，返回 true ；否則，返回 false 。

解答：

方法一：直觀

由于第二題是反轉鏈表，因此我的第一想法就是深拷貝一個新的鏈表，然后反轉此鏈表，然后在與原鏈表一個元素一個元素進行比較，這種方法比較的直觀，因此直接展示代碼：

class Solution {
public:// 主函數：判斷是否是回文鏈表bool isPalindrome(ListNode* head) {// 1. 深拷貝原鏈表ListNode* copyHead = deepCopy(head);// 2. 反轉拷貝鏈表ListNode* reversedCopy = reverseList(copyHead);// 3. 逐個比較原鏈表和反轉后的拷貝鏈表while (head && reversedCopy) {if (head->val != reversedCopy->val) {return false;}head = head->next;reversedCopy = reversedCopy->next;}// 如果兩個鏈表都走到了盡頭，說明完全匹配return true;}private:// 輔助函數1：深拷貝鏈表ListNode* deepCopy(ListNode* head) {if (!head) return nullptr;ListNode* newHead = new ListNode(head->val);ListNode* currNew = newHead;ListNode* currOld = head->next;while (currOld) {currNew->next = new ListNode(currOld->val);currNew = currNew->next;currOld = currOld->next;}return newHead;}// 輔助函數2：反轉鏈表（迭代法）ListNode* reverseList(ListNode* head) {ListNode* prev = nullptr;ListNode* curr = head;while (curr) {ListNode* nextTemp = curr->next;curr->next = prev;prev = curr;curr = nextTemp;}return prev;}
};

方法二：輔助數組

單向鏈表使用雙指針比較直比較的麻煩，但是數組使用雙指針比較值還是很快的，因此可以將鏈表中的值按照順序存儲在數組中，然后進行回文判斷。

class Solution {
public:bool isPalindrome(ListNode* head) {vector<int> assist;while (head) {assist.emplace_back(head->val);head = head->next;}int len = assist.size();for (int i = 0, j = len - 1; i < j; i++, j--) {if (assist[i] != assist[j])return false;}return true;}
};

方法三：快慢指針

這部分主要是需要找到鏈表的中間位置，這個需要如何找呢？于是就使用快慢指針了，慢指針每次前進一個位置，快指針每次前進兩個位置，這樣當快指針到達鏈表末尾時候，慢指針就到達鏈表的中間位置。具體方法參考如下鏈接：官方解答

class Solution {
public:bool isPalindrome(ListNode* head) {if (head == nullptr) {return true;}// 找到前半部分鏈表的尾節點并反轉后半部分鏈表ListNode* firstHalfEnd = endOfFirstHalf(head);ListNode* secondHalfStart = reverseList(firstHalfEnd->next);// 判斷是否回文ListNode* p1 = head;ListNode* p2 = secondHalfStart;bool result = true;while (result && p2 != nullptr) {if (p1->val != p2->val) {result = false;}p1 = p1->next;p2 = p2->next;}        // 還原鏈表并返回結果firstHalfEnd->next = reverseList(secondHalfStart);return result;}ListNode* reverseList(ListNode* head) {ListNode* prev = nullptr;ListNode* curr = head;while (curr != nullptr) {ListNode* nextTemp = curr->next;curr->next = prev;prev = curr;curr = nextTemp;}return prev;}ListNode* endOfFirstHalf(ListNode* head) {ListNode* fast = head;ListNode* slow = head;while (fast->next != nullptr && fast->next->next != nullptr) {fast = fast->next->next;slow = slow->next;}return slow;}
};

4. 環形鏈表

題目鏈接：環形鏈表
題目描述：給你一個鏈表的頭節點 head ，判斷鏈表中是否有環。

如果鏈表中有某個節點，可以通過連續跟蹤 next 指針再次到達，則鏈表中存在環。 為了表示給定鏈表中的環，評測系統內部使用整數 pos 來表示鏈表尾連接到鏈表中的位置（索引從 0 開始）。注意：pos 不作為參數進行傳遞 。僅僅是為了標識鏈表的實際情況。

如果鏈表中存在環 ，則返回 true 。 否則，返回 false 。

解答

方法一：快慢指針

這是我看到這道題目想到的第一個方法，就是使用快慢指針，快指針每次走兩步，慢指針每次走一步，要是相遇了（即兩指針指向鏈表中同一個位置），則該鏈表為環形鏈表，要是最終快指針指向空了，則該鏈表就不是環形鏈表了。
因此代碼如下：

class Solution {
public:bool hasCycle(ListNode* head) {if (head == nullptr || head->next == nullptr)return false;ListNode* slow = head;ListNode* fast = head->next;while (slow != fast) {if (fast == nullptr || fast->next == nullptr) {return false;}slow = slow->next;fast = fast->next->next;}return true;}
};

方法二：哈希表

分析題意可知，鏈表中的每個元素都是唯一的。因此，若在遍歷過程中發現某個元素已經被訪問過，則說明鏈表中存在環，此時可以直接返回結果。基于這一特性，我們可以采用哈希表來進行環的檢測。

具體做法如下：初始化一個空的哈希表，然后從頭開始遍歷鏈表。對于每一個遍歷到的節點，首先判斷其是否為 null。若當前節點為空，則表示已到達鏈表末尾，說明鏈表無環，直接返回 false；若當前節點不為空，則檢查該節點是否已經存在于哈希表中：

  • 如果存在，說明鏈表中存在環，返回 true；
  • 如果不存在，則將該節點加入哈希表，并繼續訪問下一個節點。

通過這種方式可以有效地判斷鏈表是否存在環，代碼編寫如下：

class Solution {
public:bool hasCycle(ListNode* head) {unordered_set<ListNode*> counts;ListNode* temp = head;while (temp != nullptr) {if (counts.count(temp)) {return true;}counts.insert(temp);temp = temp->next;}return false;}
};

5. 環形鏈表 II

題目鏈接：環形鏈表 II
題目描述：給定一個鏈表的頭節點 head ，返回鏈表開始入環的第一個節點。 如果鏈表無環，則返回 null。

如果鏈表中有某個節點，可以通過連續跟蹤 next 指針再次到達，則鏈表中存在環。 為了表示給定鏈表中的環，評測系統內部使用整數 pos 來表示鏈表尾連接到鏈表中的位置（索引從 0 開始）。如果 pos 是 -1，則在該鏈表中沒有環。注意：pos 不作為參數進行傳遞，僅僅是為了標識鏈表的實際情況。

不允許修改鏈表。

解答

好像還是可以使用上一道題目的兩種方法（快慢指針和哈希表），這道題目我看到的第一眼覺得哈希表更加的直觀，快慢指針其實也能做。

方法一：哈希表

在判斷鏈表中是否存在環并返回環的入口節點時，可以利用哈希表來記錄已經訪問過的節點。

具體思路如下：
遍歷鏈表中的每一個節點，對于每個節點進行如下判斷：

  • 如果該節點 已經存在于哈希表中，說明我們再次訪問到了之前已經出現過的節點，這表明鏈表中存在環，且該節點即為環的入口節點，直接返回該節點。
  • 如果該節點 尚未被訪問過，則將該節點加入哈希表中，然后繼續訪問下一個節點。

如果整個鏈表遍歷完成都沒有重復訪問到任何節點，則說明鏈表中不存在環，最終返回 nullptr。

這種方法簡單直觀，適用于大多數鏈表環檢測問題，尤其適合對空間效率要求不高的場景。若需進一步優化空間復雜度，可使用快慢指針法（Floyd 判圈算法）實現 O(1) 空間復雜度的解決方案。

class Solution {
public:ListNode* detectCycle(ListNode* head) {if (head == nullptr || head->next == nullptr)return nullptr;unordered_set<ListNode*> seen;ListNode* temp = head;while (temp != nullptr) {if (seen.count(temp)) {return temp;}seen.insert(temp);temp = temp->next;}return nullptr;}
};

方法二：快慢指針

這個方法涉及到一些數學公式的推導，具體的文字解釋詳見官方解答

在這里插入圖片描述
下面解釋為什么在快慢指針相遇時，慢指針移動的距離 b b b 不會超過環的長度。

假設在相遇前，慢指針已經在環內繞行了一圈以上，那么快指針在這段時間內必然已經繞行了兩圈以上。由于快指針的速度是慢指針的兩倍，因此在慢指針進入環后、完成一圈之前，快指針就已經追上了它。

這就意味著，在慢指針繞完第一圈的過程中，快指針必定會在某一時刻從后面追上慢指針，兩者相遇。因此，在快慢指針第一次相遇時，慢指針尚未走完整個環一圈，即移動距離 b b b 必然小于環的總長度。

class Solution {
public:ListNode* detectCycle(ListNode* head) {ListNode *slow = head, *fast = head;while (fast != nullptr) {slow = slow->next;if (fast->next == nullptr)return nullptr;fast = fast->next->next;if (slow == fast) {ListNode* ptr = head;while (ptr != slow) {ptr = ptr->next;slow = slow->next;}return ptr;}}return nullptr;}
};

6. 合并兩個有序鏈表

題目鏈接：合并兩個有序鏈表
題目描述：將兩個升序鏈表合并為一個新的 升序 鏈表并返回。新鏈表是通過拼接給定的兩個鏈表的所有節點組成的。

解答

思路比較簡單，但是編碼需要注意的事項比較多

方法一：遞歸

遞歸嘛，就是選擇兩個鏈表頭部值較小的一個節點與剩下元素的 merge 操作結果合并。對于邊界情況特殊處理即可。

class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if (list1 == nullptr)return list2;else if (list2 == nullptr)return list1;else if (list1->val < list2->val) {list1->next = mergeTwoLists(list1->next, list2);return list1;} else {list2->next = mergeTwoLists(list1, list2->next);return list2;}}
};

方法二：迭代

? 函數簽名

ListNode* mergeTwoLists(ListNode* list1, ListNode* list2)
  • 輸入：兩個指向 ListNode 的指針，分別表示兩個有序鏈表的頭節點。
  • 輸出：一個指向合并后新鏈表頭節點的指針。

🔁 主要邏輯步驟

  1. 邊界處理：

    • 如果其中一個鏈表為空，則直接返回另一個鏈表（即未空的那一個）。

  2. 使用虛擬頭節點構建結果鏈表：

    • 創建一個虛擬頭節點 head（值為 0），用于簡化插入操作。
    • 使用指針 curr 跟蹤當前插入位置。

  3. 雙指針遍歷兩個鏈表：

    • 同時遍歷 list1 和 list2，每次比較當前節點的值：
      • 取較小值創建新節點，并將其連接到 curr->next。
      • 移動對應鏈表的指針（list1 或 list2）和 curr 指針。

  4. 處理剩余部分：

    • 當其中一個鏈表遍歷完成后，將另一個鏈表剩余的部分直接接在 curr->next 后面。

  5. 返回結果：

    • 返回 head->next，即合并后鏈表的第一個有效節點。

?? 時間與空間復雜度分析

類型復雜度說明
時間復雜度O(m + n)其中 m 和 n 分別是兩個鏈表的長度，每個節點最多訪問一次
空間復雜度O(m + n)新建了一個鏈表來保存合并后的結果
class Solution
{
public:ListNode *mergeTwoLists(ListNode *list1, ListNode *list2){if (list1 == nullptr)return list2;if (list2 == nullptr)return list1;ListNode *head = new ListNode(0);ListNode *curr = head;while (list1 != nullptr && list2 != nullptr){int val = 0;if (list1->val <= list2->val){val = list1->val;list1 = list1->next;}else{val = list2->val;list2 = list2->next;}curr->next = new ListNode(val);curr = curr->next;}if (list1 == nullptr)curr->next = list2;else if (list2 == nullptr)curr->next = list1;return head->next;}
};

或者 w h i l e while while 語句可以寫成如下的形式：

while (list1 != nullptr && list2 != nullptr) {if (list1->val <= list2->val) {curr->next = new ListNode(list1->val);list1 = list1->next;} else {curr->next = new ListNode(list2->val);list2 = list2->next;}curr = curr->next;}

7. 兩數相加

題目鏈接：兩數相加
題目描述：給你兩個 非空 的鏈表，表示兩個非負的整數。它們每位數字都是按照 逆序 的方式存儲的，并且每個節點只能存儲 一位 數字。

請你將兩個數相加，并以相同形式返回一個表示和的鏈表。

你可以假設除了數字 0 之外，這兩個數都不會以 0 開頭。

解答

反正這道題目我也不知道使用的是啥方法，我寫的代碼原本如下（又臭又長）：

class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {ListNode* head = new ListNode(0);ListNode* curr = head;int temp = 0;// 同時遍歷兩個鏈表的部分while (l1 != nullptr && l2 != nullptr) {int sum = l1->val + l2->val + temp;if (sum > 9) {curr->next = new ListNode(sum % 10);temp = 1;} else {curr->next = new ListNode(sum);temp = 0;}curr = curr->next;l1 = l1->next;l2 = l2->next;}// 處理 l2 剩余部分if (l1 == nullptr) {while (l2 != nullptr || temp > 0) {if (l2 == nullptr) {curr->next = new ListNode(temp);temp = 0;} else {int sum = l2->val + temp;if (sum > 9) {curr->next = new ListNode(sum % 10);temp = 1;} else {curr->next = new ListNode(sum);temp = 0;}l2 = l2->next;}curr = curr->next;}}// 處理 l1 剩余部分if (l2 == nullptr) {while (l1 != nullptr || temp > 0) {if (l1 == nullptr) {curr->next = new ListNode(temp);temp = 0;} else {int sum = l1->val + temp;if (sum > 9) {curr->next = new ListNode(sum % 10);temp = 1;} else {curr->next = new ListNode(sum);temp = 0;}l1 = l1->next;}curr = curr->next;}}return head->next;}
};

還是官方的代碼簡潔巧妙，學到了，官方認為：如果兩個鏈表的長度不同，則可以認為長度短的鏈表的后面有若干個 0 ，這樣的話，可以相當于兩個鏈表是一樣長的。

class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {ListNode* head = new ListNode(0);ListNode* curr = head;int carry = 0;while (l1 != nullptr || l2 != nullptr || carry > 0) {int x = (l1 != nullptr) ? l1->val : 0;int y = (l2 != nullptr) ? l2->val : 0;int sum = x + y + carry;carry = sum / 10;curr->next = new ListNode(sum % 10);curr = curr->next;if (l1 != nullptr)l1 = l1->next;if (l2 != nullptr)l2 = l2->next;}return head->next;}
};

8. 刪除鏈表的倒數第 N 個結點

題目鏈接：刪除鏈表的倒數第 N 個結點
題目描述：給你一個鏈表，刪除鏈表的倒數第 n 個結點，并且返回鏈表的頭結點。

解答

一開始我也不知道為啥會寫出下面的代碼，邏輯上沒有問題，但是超時了（內存泄露等問題）。

class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {vector<int> value;ListNode* curr = head;while (curr != nullptr) {value.push_back(curr->val);curr = curr->next;}int len = value.size();int del_pos = len - n;ListNode* new_head = new ListNode(0);curr = new_head;int i = 0;while (i < len) {int temp = value[i];if (i == del_pos)continue;i++;curr->next = new ListNode(temp);curr = curr->next;}return new_head->next;}
};

方法一：二次遍歷

既然超時了，那我又有了以下的想法：

  • 先遍歷一遍鏈表，統計節點個數 num；
  • 然后計算出要刪除的是“正數第 del_pos = num - n” 個節點；
  • 再次從頭開始遍歷，走到那個位置進行刪除。

上述需要注意頭節點的刪除需要特殊處理
于是代碼編寫如下：

class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {int num = 0;ListNode* curr = head;// 第一次遍歷：統計節點個數while (curr != nullptr) {num++;curr = curr->next;}// 需要刪除節點的位置int del_pos = num - n;// 特判：刪除頭節點if (del_pos == 0) {ListNode* newHead = head->next;delete head;return newHead;}// 第二次遍歷：找到要刪除節點的前一個節點curr = head;int count = 0;while (curr != nullptr && curr->next != nullptr) { // 防止空指針if (count == del_pos - 1) {// 找到前一個節點，刪除后一個節點ListNode* toDelete = curr->next;curr->next = toDelete->next;delete toDelete;break;}curr = curr->next;count++;}return head;}
};

方法二：棧

這方法不錯，利用棧的特性，將全部節點壓入棧，然后彈棧時即可判斷需要刪除的節點。

class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {ListNode* dummy = new ListNode(0, head);stack<ListNode*> stk;ListNode* curr = dummy;while (curr) {stk.push(curr);curr = curr->next;}for (int i = 0; i < n; i++)stk.pop();ListNode* prev = stk.top();prev->next = prev->next->next;ListNode* ans = dummy->next;delete dummy;return ans;}
};

方法三：雙指針

這個方法比較的巧妙，不同于快慢指針的遍歷速度不同，這個雙指針遍歷速度一樣，只是中間需要隔一段距離，而這個距離是由題目需要刪除節點的位置決定的。引入一個啞結點（dummy），這樣通過上述方式即可找到需要刪除節點的前驅節點，這樣就能更好的刪除了。
官方的可視化的一個例子很好的說明了這個方法：
在這里插入圖片描述
基于上述原理，可以編寫代碼如下：

class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {// 創建一個虛擬頭節點 dummy，并讓它指向原始鏈表的頭節點 head// dummy 的作用是簡化邊界情況（如刪除頭節點）ListNode* dummy = new ListNode(0, head);// 定義兩個指針：ListNode* first = head;   // 快指針ListNode* second = dummy; // 慢指針，初始時指向 dummy// 快指針先向前移動 n 步for (int i = 0; i < n; i++) {first = first->next;}// 然后快慢指針一起向前移動，直到快指針到達鏈表末尾while (first != nullptr) {first = first->next;   // 快指針繼續前移second = second->next; // 慢指針同步前移}// 此時，second 指向要刪除節點的前一個節點// 刪除目標節點（即 second->next）ListNode* nodeToDelete = second->next;         // 保存要刪除的節點second->next = second->next->next;              // 跳過目標節點delete nodeToDelete;                            // 釋放內存（C++ 中重要）// 保存結果頭節點（可能不是原始 head，因為 dummy 是虛擬頭節點）ListNode* ans = dummy->next;// 最后釋放 dummy 節點的內存delete dummy;// 返回最終結果return ans;}
};

9. 兩兩交換鏈表中的節點

題目鏈接：兩兩交換鏈表中的節點
題目描述：給你一個鏈表，兩兩交換其中相鄰的節點，并返回交換后鏈表的頭節點。你必須在不修改節點內部的值的情況下完成本題（即，只能進行節點交換）。

解答

這道題目主要是需要知道這個交換的節點是啥，我一開始沒有看懂啥叫兩兩交換鏈表中的結點，詢問 a i ai ai 發現就是每次處理兩個節點，把它們的位置調換。例如：

原始順序是：A → B → C → D

交換后是：B → A → D → C

每兩個一組交換，直到鏈表末尾。
也就是說，這一組只在組內交換，不和其他的組進行交換，比如上述 A A A 交換后不與后面的 C C C 進行交換了。

再弄懂了題目的大致意思后，于是我就有了兩種初始的想法，一種就是模擬，直接設置兩個指針，然后逐漸遍歷下去，直到交換完成，還有一種就是遞歸的方式（這種代碼簡單，但是不好想）。

方法一：模擬

我使用的模擬的思路大致如下：

  • 使用一個虛擬頭節點 d u m m y dummy dummy 來簡化邊界情況。
  • 維護三個指針：
    • p r e v prev prev ：前一個節點（用來連接新的交換后的節點）
    • f i r s t first first ：當前組的第一個節點
    • s e c o n d second second ：當前組的第二個節點
  • 每次循環中完成一次交換，并移動指針到下一組。

在有了上述的思路后，于是代碼編寫就不是很難了，

class Solution {
public:ListNode* swapPairs(ListNode* head) {// 創建一個啞結點，指向頭節點，簡化返回ListNode* dummy = new ListNode(0, head);ListNode* prev = dummy;// ListNode* first = head;while (head != nullptr && head->next != nullptr) {ListNode* first = head;ListNode* second = head->next;prev->next = first->next;first->next = second->next;second->next = first;prev = first; // 此時的 first節點就類似于下一組的啞結點，按照循環直接處理即可head = first->next;}return dummy->next;}
};

方法二：迭代

在經過上述模擬的方法，可以知道，其實每次交換使用的方法幾乎都是一樣的，因此還可以使用迭代的方法進行交換，思路如下：

  • 如果鏈表為空或只有一個節點，直接返回。
  • 否則，先交換前兩個節點。
  • 然后讓后面的部分遞歸地去交換。
  • 最后返回新的頭節點。

于是代碼可以編寫如下：

class Solution {
public:ListNode* swapPairs(ListNode* head) {// 邊界判斷：如果鏈表為空 或者 只剩一個節點，無法交換，直接返回原頭節點if (head == nullptr || head->next == nullptr) return head;// 定義第一個節點ListNode* first = head;// 定義第二個節點（一定是 first 的下一個）ListNode* second = first->next;// 關鍵步驟1：// 把 first 的 next 指向「從 second 之后的節點開始交換后的結果」// 這里使用了遞歸，swapPairs(second->next) 表示對后面未處理的部分進行同樣的操作。// 比如在 1 -> 2 -> 3 -> 4 中：// first 是 1，second 是 2，// swapPairs(3) 就是處理 3 -> 4 的結果（即 4 -> 3），// 所以現在 first（1）的 next 應該指向 4 -> 3 的頭節點 4first->next = swapPairs(second->next);// 關鍵步驟2：// 把 second 的 next 指向 first，完成當前這對節點的交換// 原來是 first -> second，現在變成 second -> firstsecond->next = first;// 返回值是 second，因為交換后 second 成為了這一段的新頭節點// 比如上面的例子中，交換 1 -> 2 后變成 2 -> 1，// 所以返回的是 second（即 2），作為這一層遞歸的新頭節點return second;}
};

評論解答區看到一個有意思的解答

class Solution {
public:ListNode* swapPairs(ListNode* head) {vector<ListNode*> vec;ListNode *ans = new ListNode(0, nullptr), *pre = ans;while (head) {vec.emplace_back(head);head = head->next;}for (int i = 0, j = 1; j < vec.size(); i += 2, j += 2) {pre->next = vec[j];pre = pre->next;pre->next = vec[i];pre = pre->next;}if (vec.size() % 2) {pre->next = vec[vec.size() - 1];pre = pre->next;}pre->next = nullptr;return ans->next;}
};

上述代碼就是直接將節點中的值存儲起來了，然后新建一個鏈表，然后存儲對應位置的值，返回即可，雖然不符合題目要求，但是也算是一種解題方法。

10. K 個一組翻轉鏈表

題目鏈接：K 個一組翻轉鏈表
題目描述：給你鏈表的頭節點 head ，每 k 個節點一組進行翻轉，請你返回修改后的鏈表。

k 是一個正整數，它的值小于或等于鏈表的長度。如果節點總數不是 k 的整數倍，那么請將最后剩余的節點保持原有順序。

你不能只是單純的改變節點內部的值，而是需要實際進行節點交換。

解答

前面寫過反轉鏈表，因此這里就只需要將鏈表劃分為 k k k 組，最后不足 k k k 組的直接不翻轉，直接拼接即可。接著對于一些邊界仔細處理，各組之間鏈表的連接仔細處理即可，然后就可以得到答案了。

class Solution {
private:// 翻轉從 head 開始的 k 個節點，并返回新的頭節點ListNode* reverseList(ListNode* head, int k) {ListNode* prev = nullptr;ListNode* curr = head;while (k--) {ListNode* next = curr->next;curr->next = prev;prev = curr;curr = next;}return prev; // 新的頭節點是 prev}
public:// K 個一組翻轉鏈表主函數ListNode* reverseKGroup(ListNode* head, int k) {// 邊界情況：空鏈表或 k == 1（無需翻轉）if (!head || k == 1)return head;// 創建一個虛擬頭節點，簡化頭節點翻轉時的處理ListNode* dummy = new ListNode(0, head);// prev 指向前一組的最后一個節點，用來連接下一組翻轉后的頭節點ListNode* prev = dummy;// curr 指向當前要處理的節點ListNode* curr = head;// 遍歷整個鏈表while (curr) {// 檢查是否有足夠的節點進行翻轉（至少 k 個）ListNode* tail = prev; // 嘗試找到第 k 個節點for (int i = 0; i < k; ++i) {tail = tail->next;if (!tail) { // 不足 k 個節點，保留原樣，直接返回結果return dummy->next;}}// 找到了可以翻轉的 k 個節點，開始翻轉ListNode* next_group = tail->next; // 記錄下一組的起始點ListNode* group_head = curr;       // 當前組的頭節點// 翻轉這 k 個節點ListNode* new_head = reverseList(group_head, k);// 連接翻轉后的這一組和前一部分prev->next = new_head;// 把當前組翻轉后的尾節點（即原來的頭）指向下一組的開始group_head->next = next_group;// 更新指針，準備處理下一組prev = group_head; // 原來的頭變成了尾curr = next_group; // 移動到下一組開始位置}// 返回最終結果（dummy 的下一個節點是新的頭節點）return dummy->next;}
};

思路還是挺好想到的，但是轉化為代碼就不是很好編寫了，需要考慮眾多因素。

11. 隨機鏈表的復制

題目鏈接：隨機鏈表的復制
題目描述：給你一個長度為 n 的鏈表，每個節點包含一個額外增加的隨機指針 random ，該指針可以指向鏈表中的任何節點或空節點。

構造這個鏈表的 深拷貝。 深拷貝應該正好由 n 個 全新 節點組成，其中每個新節點的值都設為其對應的原節點的值。新節點的 next 指針和 random 指針也都應指向復制鏈表中的新節點，并使原鏈表和復制鏈表中的這些指針能夠表示相同的鏈表狀態。復制鏈表中的指針都不應指向原鏈表中的節點 。

解答

對于普通鏈表的復制，直接可以按照遍歷的順序創建鏈表節點，但是這道題目由于存在隨機指針，可能當前結點的隨機指針指向的節點還沒有常見，因此我的想法是需要遍歷兩邊，第一遍先創建出來所有的結點，第二便在確定 n e x t next next 指針和 r a n d o m random random 指向的節點。于是可以編寫代碼如下：

class Solution {
public:unordered_map<Node*, Node*> hmap;Node* copyRandomList(Node* head) {Node* p = head;while (p) {hmap.insert({p, new Node(p->val)});p = p->next;}p = head;while (p) {hmap[p]->next = (p->next != nullptr) ? hmap[p->next] : nullptr;hmap[p]->random =(p->random != nullptr) ? hmap[p->random] : nullptr;p = p->next;}return hmap[head];}
};

12. 排序鏈表

題目鏈接：排序鏈表
題目描述：給你鏈表的頭結點 head ，請將其按 升序 排列并返回 排序后的鏈表 。

解答

方法一：輔助數組

看到這道題的第一反應是考慮排序。然而，直接對鏈表進行排序操作較為復雜，效率也不高。因此，我想到借助數組來簡化這一過程。
具體思路如下：

  • 遍歷原始鏈表，將所有節點依次存入一個數組中；
  • 對這個數組進行排序（根據節點的值）；
  • 然后將排好序的節點重新賦值給原始鏈表
  • 返回原始鏈表的頭節點
class Solution {
public:ListNode* sortList(ListNode* head) {vector<int> cache_val;ListNode* p = head;while (p) {cache_val.push_back(p->val);p = p->next;}sort(cache_val.begin(), cache_val.end());int len = cache_val.size();p = head;int i = 0;while (p && i < len) {p->val = cache_val[i];i++;p = p->next;}return head;}
};

方法二：遞歸實現的歸并排序

歸并排序是一種典型的 分治算法（Divide and Conquer），它適用于需要穩定排序的場景。鏈表結構天然適合歸并排序的原因有：

  • 不需要像數組那樣頻繁移動元素；
  • 可以通過指針操作輕松拆分和合并鏈表。

整個算法分為三步：

步驟描述
分使用快慢指針將鏈表從中間斷開為兩個子鏈表
治對每個子鏈表遞歸進行歸并排序
合將兩個有序鏈表合并成一個有序鏈表

于是代碼編寫如下：

class Solution {
public:// 主函數：排序鏈表ListNode* sortList(ListNode* head) { return mergeSort(head); }
private:// 歸并排序主函數ListNode* mergeSort(ListNode* head) {// 小于等于1個節點的話，直接返回if (!head || !head->next)return head;// 1. 快慢指針找中點ListNode *slow = head, *fast = head, *prev = nullptr;while (fast && fast->next) {prev = slow;slow = slow->next;fast = fast->next->next;}// 2. 斷開鏈表，prev找到了鏈表中點的位置prev->next = nullptr;// 3. 分治ListNode* left = mergeSort(head);ListNode* right = mergeSort(slow);// 4. 合并return merge(left, right);}// 合并兩個有序鏈表ListNode* merge(ListNode* l1, ListNode* l2) {// ListNode* dummy = new ListNode(0);// ListNode* curr = dummy;// 注釋起來的寫法也是可以的,但是返回的值需要寫return dummy->next;ListNode dummy(0);ListNode* curr = &dummy;while (l1 != nullptr && l2 != nullptr) {if (l1->val < l2->val) {curr->next = l1;l1 = l1->next;} else {curr->next = l2;l2 = l2->next;}curr = curr->next;}curr->next = l1 ? l1 : l2;// 注釋起來的寫法也是可以的// if (l1 != nullptr)//     curr->next = l1;// if (l2 != nullptr)//     curr->next = l2;return dummy.next;}
};

方法三：自底向上歸并排序

這個方法看官方解答吧，感覺原理還是很好懂的，但是編碼可能需要注意的地方比較的多：
官方解答

class Solution {
public:// 主函數：對鏈表進行排序ListNode* sortList(ListNode* head) {if (!head || !head->next)return head;// 1. 先遍歷一次鏈表，獲取總長度int length = getLength(head);// 創建一個虛擬頭節點，方便操作整個鏈表ListNode dummy(0, head);ListNode* curr = head;ListNode* prev = &dummy;// 2. 開始 Bottom-Up 歸并排序，從子段長度 1 開始，逐步翻倍for (int subLength = 1; subLength < length; subLength *= 2) {prev = &dummy;curr = dummy.next; // 從原始鏈表開頭開始處理// 對當前鏈表按 subLength 分割成多個子段并兩兩合并while (curr != nullptr) {// 第一段 l1 的起點是 currListNode* l1 = curr;// 找到第一段的結尾，并斷開它for (int i = 1; i < subLength && curr->next != nullptr; ++i) {curr = curr->next;}ListNode* l2 = curr->next;curr->next = nullptr; // 斷開 l1// 移動 curr 到 l2 的位置curr = l2;// 找到第二段的結尾，并斷開它for (int i = 1; i < subLength && curr != nullptr && curr->next != nullptr;++i) {curr = curr->next;}// 保存下一輪的起點ListNode* next = nullptr;if (curr != nullptr) {next = curr->next;curr->next = nullptr; // 斷開 l2}// 合并兩個有序子鏈表ListNode* merged = merge(l1, l2);// 把合并后的鏈表接到 prev 后面prev->next = merged;// 更新 prev 到合并后鏈表的末尾while (prev->next != nullptr) {prev = prev->next;}// 下一輪從這里繼續處理curr = next;}}// 返回排序后的鏈表頭節點return dummy.next;}private:// 獲取鏈表長度int getLength(ListNode* head) {int len = 0;while (head) {++len;head = head->next;}return len;}// 合并兩個有序鏈表（標準寫法）ListNode* merge(ListNode* l1, ListNode* l2) {ListNode dummy(0); // 虛擬頭節點ListNode* tail = &dummy;while (l1 && l2) {if (l1->val < l2->val) {tail->next = l1;l1 = l1->next;} else {tail->next = l2;l2 = l2->next;}tail = tail->next;}// 接上剩余部分tail->next = l1 ? l1 : l2;return dummy.next;}
};

13. 合并 K 個升序鏈表

題目鏈接：合并 K 個升序鏈表
題目描述：給你一個鏈表數組，每個鏈表都已經按升序排列。

請你將所有鏈表合并到一個升序鏈表中，返回合并后的鏈表。

解答

方法一：分治法

看到這道題目我就覺得首先肯定是需要用到之前的 合并兩個有序鏈表 的思想，但是這里由于有 k k k 個鏈表，因此不能簡單的進行排序處理，于是我就想到了分治的方法，每次合并后，鏈表的數量變成原來的兩倍，一直重復下去，直到得到最終的有序鏈表，官方可視化解釋如下：在這里插入圖片描述
代碼如下：

class Solution {
private:// 對兩個有序鏈表進行排序，之前的題目中有對應的實現ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if (list1 == nullptr || list2 == nullptr)return list1 ? list1 : list2;ListNode* dummy = new ListNode(0);ListNode* head = dummy;while (list1 && list2) {if (list1->val < list2->val) {head->next = list1;list1 = list1->next;} else {head->next = list2;list2 = list2->next;}head = head->next;}head->next = list1 ? list1 : list2;return dummy->next;}// 分治法進行排序ListNode* merge(vector<ListNode*>& lists, int left, int right) {if (left == right)return lists[left];if (left > right)return nullptr;int mid = (left + right) >> 1;return mergeTwoLists(merge(lists, left, mid),merge(lists, mid + 1, right));}public:ListNode* mergeKLists(vector<ListNode*>& lists) {int len = lists.size();return merge(lists, 0, len - 1);}
};

方法二：順序實現

也是需要自己編寫兩個有序鏈表的合并，然后直接遍歷這 k k k 個列表，每次遍歷一個調用合并函數即可。

class Solution {
private:// 合并兩個有序鏈表ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if (list1 == nullptr || list2 == nullptr)return list1 ? list1 : list2;ListNode* dummy = new ListNode(0);ListNode* head = dummy;while (list1 && list2) {if (list1->val < list2->val) {head->next = list1;list1 = list1->next;} else {head->next = list2;list2 = list2->next;}head = head->next;}head->next = list1 ? list1 : list2;return dummy->next;}
public:ListNode* mergeKLists(vector<ListNode*>& lists) {ListNode* ans = nullptr;for (size_t i = 0; i < lists.size(); ++i) {ans = mergeTwoLists(ans, lists[i]);}return ans;}
};

14. LRU 緩存

題目鏈接：LRU 緩存
題目描述：在這里插入圖片描述

解答

這題直接看題解吧，我感覺我要是研究生面試應該是不會問到這類的算法題的

官方解答

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/87064.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/87064.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/87064.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

Web前端基礎之HTML

Web前端基礎之HTML

一、瀏覽器 火狐瀏覽器、谷歌瀏覽器(推薦)、IE瀏覽器 推薦谷歌瀏覽器原因&#xff1a; 1、簡潔大方,打開速度快 2、開發者調試工具&#xff08;右鍵空白處->檢查&#xff0c;打開調試模式&#xff09; 二、開發工具 核心IDE工具 Visual Studio Code (VS Code)? 微軟開發…
閱讀更多...
11.TCP三次握手

11.TCP三次握手

TCP連接建立與傳輸 1&#xff0e;主機 A 與主機 B 使用 TCP 傳輸數據&#xff0c;A 是 TCP 客戶&#xff0c;B 是 TCP 服務器。假設有512B 的數據要傳輸給 B&#xff0c;B 僅給 A 發送確認&#xff1b;A 的發送窗口 swnd 的尺寸為 100B&#xff0c;而 TCP 數據報文段每次也攜帶…
閱讀更多...
Python 爬蟲入門 Day 3 - 實現爬蟲多頁抓取與翻頁邏輯

Python 爬蟲入門 Day 3 - 實現爬蟲多頁抓取與翻頁邏輯

Python 第二階段 - 爬蟲入門 &#x1f3af; 今日目標 掌握網頁分頁的原理和定位“下一頁”的鏈接能編寫循環邏輯自動翻頁抓取內容將多頁抓取整合到爬蟲系統中 &#x1f4d8; 學習內容詳解 &#x1f501; 網頁分頁邏輯介紹 以 quotes.toscrape.com 為例&#xff1a; 首頁鏈…
閱讀更多...
分布式定時任務系列12：XXL-job的任務觸發為什么是死循環？

分布式定時任務系列12：XXL-job的任務觸發為什么是死循環？

傳送門 分布式定時任務系列1&#xff1a;XXL-job安裝 分布式定時任務系列2&#xff1a;XXL-job使用 分布式定時任務系列3&#xff1a;任務執行引擎設計 分布式定時任務系列4&#xff1a;任務執行引擎設計續 分布式定時任務系列5&#xff1a;XXL-job中blockingQueue的應用 …
閱讀更多...
位運算詳解之異或運算的奇妙操作

位運算詳解之異或運算的奇妙操作

位運算詳解之異或運算的奇妙操作 一、異或運算的本質與核心性質1.1 異或運算的定義與邏輯規則1.2 異或運算的核心代數性質&#xff08;1&#xff09;自反性&#xff1a;a ^ a 0&#xff08;2&#xff09;恒等性&#xff1a;a ^ 0 a&#xff08;3&#xff09;交換律&#xff1…
閱讀更多...
Element Plus 去除下拉菜單周黑邊

Element Plus 去除下拉菜單周黑邊

問題&#xff1a; 如上圖所示&#xff0c;當鼠標移入&#xff08;hover&#xff09;和點擊時就會圍繞一圈黑色邊框&#xff0c;但通過本文的方案 100% 完美解決。 解決方案: :deep(:focus-visible) {outline: none; } 備用方案 :deep(.el-tooltip__trigger:focus-visible) …
閱讀更多...
React Native 項目實戰 —— 記賬本應用開發指南

React Native 項目實戰 —— 記賬本應用開發指南

React Native 項目實戰 —— 記賬本應用開發指南 項目概述&#xff1a;本文將指導您使用 React Native 開發一個簡單的記賬本應用&#xff0c;幫助用戶記錄收入和支出。核心內容&#xff1a;我們將分析功能模塊、設計接口、劃分組件結構、管理數據流、實現頁面跳轉&#xff0c…
閱讀更多...
從 PPO、DPO 到 GRPO：大語言模型策略優化算法解析

從 PPO、DPO 到 GRPO：大語言模型策略優化算法解析

從 PPO、DPO 到 GRPO&#xff1a;大語言模型策略優化算法解析 背景與簡介 大語言模型&#xff08;LLM&#xff09;的訓練通常分為預訓練和后訓練兩個階段。預訓練階段&#xff0c;模型在海量文本上學習下一詞預測的能力&#xff1b;后訓練階段&#xff0c;我們希望進一步對齊…
閱讀更多...
React中使用Day.js指南

React中使用Day.js指南

文章目錄 引言什么是Day.js&#xff1f;Day.js的核心特性 安裝和基礎配置安裝Day.js基礎導入和使用 在React中的基礎使用1. 顯示格式化日期2. 實時時鐘組件 常用插件配置1. 相對時間插件2. 高級格式化插件3. 時區處理插件 實戰案例&#xff1a;博客文章時間組件高級應用場景1. …
閱讀更多...
【系統設計【1】】系統設計面試方法論：從0到百萬用戶的需求到架構的推演

【系統設計【1】】系統設計面試方法論：從0到百萬用戶的需求到架構的推演

文章目錄 一、系統設計面試的底層邏輯&#xff1a;從需求到架構的推演&#xff08;一&#xff09;需求澄清&#xff1a;界定問題邊界&#xff08;二&#xff09;分層設計&#xff1a;從單節點到分布式的演進1. Web層&#xff1a;無狀態化與負載均衡2. 數據層&#xff1a;數據庫…
閱讀更多...
京津冀城市群13城市空間權重0-1矩陣

京津冀城市群13城市空間權重0-1矩陣

京津冀城市群13城市空間權重0-1矩陣 1、數據說明&#xff1a;京津冀13個城市&#xff1a;北京市、保定市、滄州市、承德市、邯鄲市、衡水市、廊坊市、秦皇島市、石家莊市、唐山市、邢臺市、張家口市、天津市、 2、指標解釋&#xff1a;空間權重矩陣是一種用于表征空間表達式的…
閱讀更多...
七大技術路線解析：自動駕駛如何被數據重新定義

七大技術路線解析：自動駕駛如何被數據重新定義

自動駕駛技術從實驗室的算法驗證走向大規模量產應用&#xff0c;是一場充滿挑戰的征程。這段征程的核心驅動力&#xff0c;不僅是芯片和傳感器的升級&#xff0c;更是一場關于數據的“喂養”競賽——從簡單的像素標注到多模態大模型的理解&#xff0c;數據需求的演變悄然推動著…
閱讀更多...
計網復習知識（16）傳輸層及其協議功能

計網復習知識（16）傳輸層及其協議功能

目錄 考研大綱 1.傳輸層概述 端口號 有連接/無連接傳輸 可靠/不可靠傳輸 2.UDP協議 2.1 udp數據報 2.2 udp檢驗 3.TCP協議 3.1 TCP協議的框架梳理 3.2 TCP報文段**** 3.3 三次握手與四次揮手 三次握手 四次揮手 3.4 可靠傳輸與流量控制 流量控制&#xff1a;滑動…
閱讀更多...
每天一個前端小知識 Day 1

每天一個前端小知識 Day 1

語義化 HTML&#xff08;Semantic HTML&#xff09; 1. 什么是語義化 HTML&#xff1f; 語義化 HTML 指的是使用符合內容含義的標簽&#xff0c;而不僅僅為了布局或樣式。例如&#xff1a; <article>…</article> <nav>…</nav> <header>…&l…
閱讀更多...
在docker中部署mysql

在docker中部署mysql

部署 MySQL&#xff08;端口 9006&#xff09; 1. 創建數據目錄 mkdir -p ~/qihuang/mysql/data2. 啟動 MySQL 容器 docker run -d \--name mysql-qihuang \-p 9006:3306 \-v ~/qihuang/mysql/data:/var/lib/mysql \-e MYSQL_ROOT_PASSWORDroot \-e MYSQL_DATABASEqihuangdb…
閱讀更多...
JavaScript基礎-事件對象

JavaScript基礎-事件對象

一、前言 在前端開發中&#xff0c;用戶與頁面的交互行為&#xff08;如點擊按鈕、輸入文本、滾動頁面等&#xff09;都會觸發相應的事件。而這些事件發生時&#xff0c;瀏覽器會自動創建一個 事件對象&#xff08;Event Object&#xff09;&#xff0c;它包含了當前事件的所有…
閱讀更多...
藍橋杯_染色_bfs_Java

藍橋杯_染色_bfs_Java

臨時抱抱佛腳&#xff0c;太浮躁了&#xff0c;藍橋杯已經快1個半月沒做題了。 本人比較菜&#xff0c;感覺這個時間節點也只能把暴力題給盡量多做做&#xff0c;找找做題手感&#xff0c;其他就純憑運氣了吧。T-T。 題目 問題描述 小藍有一個 n 行 m 列的白色棋盤, 棋盤的每一…
閱讀更多...
MySQL 究極奧義·動態乾坤大挪移·無敵行列轉換術

MySQL 究極奧義·動態乾坤大挪移·無敵行列轉換術

導入大SQL文件 [mysqld] # 大批量導入優化 bulk_insert_buffer_size1G max_allowed_packet1G innodb_autoextend_increment512M innodb_buffer_pool_size4G innodb_log_buffer_size4G innodb_log_file_size4G動態行列轉換 DROP TABLE IF EXISTS tb_score;CREATE TABLE tb_sco…
閱讀更多...
Excel大廠自動化報表實戰(互聯網金融-數據分析周報制作中)

Excel大廠自動化報表實戰(互聯網金融-數據分析周報制作中)

這是Excel大廠自動化報表實戰第三期--互聯網金融-數據分析周報制作中 數據資源已經與這篇博客捆綁&#xff0c;有需要者可以下載通過網盤分享的文件&#xff1a;2.4自動化報表-8月成交數據.xlsx&#xff0c;2.4自動化報表-8月獲客數據.csv等2個文件 鏈接: https://pan.baidu.c…
閱讀更多...
langchain從入門到精通（七）——利用回調功能調試鏈應用 - 讓過程更透明

langchain從入門到精通（七）——利用回調功能調試鏈應用 - 讓過程更透明

1. Callback 功能介紹 Callback 是 LangChain 提供的回調機制&#xff0c;允許我們在 LLM 應用程序的各個階段使用 hook &#xff08;鉤子&#xff09;。鉤子的含義也非常簡單&#xff0c;我們把應用程序看成一個一個的處理邏輯&#xff0c;從開始到結束&#xff0c;鉤子就是在…
閱讀更多...
最新文章

Copyright @ 2022~2023