目錄

🔍 若用遞歸計算每一項，會發生什么？

Horner's Rule（霍納法則）

?第一步：我們從最原始的泰勒公式出發

第二步：從形式上重新觀察展開式?

🌟 第三步：引出霍納法則（Horner’s Rule）

?第四步：如何用這個結構重寫泰勒展開式？?

完整代碼

?從迭代轉換成遞歸邏輯

“迭代”和“循環”?

---

當前遞歸方法的結構回顧：

double num = 1, den = 1;double taylor(int n, double x) {if (n == 0) return 1;double res = taylor(n - 1, x);  // 一次函數調用num *= x;                       // 分子：一次乘法den *= n;                       // 分母：一次乘法return res + num / den;
}

這一版已經做了初步優化：我們通過 累計 num 和 den 來避免重復調用 pow(x,n) 和 factorial(n)。

但這只是相對優化，我們現在要分析：

🔍 若用遞歸計算每一項，會發生什么？

我們從第 0 項到第 n 項共計算 n+1項，每一項的乘法成本如下：

第 k 項	乘法次數
k = 0	0
k = 1	1
k = 2	2
...	...
k = n	n

所以總乘法次數為：

? 因此，乘法總次數為 O(n^2）！

🚨 問題在哪里？

• 你對每一項都重新計算冪和階乘

• 導致重復計算，浪費大量 CPU 時間

• 如果你希望 n = 50、n = 100，程序變慢得很明顯

🤔 有沒有更好的方式？

是的。你就引出了今天的主角：

Horner's Rule（霍納法則）

我們可以嘗試換一種展開方式，讓我們不必每次都分別去計算冪和階乘。

我們將展開式進行重寫：

也就是一種嵌套式計算結構。

這個就是 Horner 法則的思路 —— 逐層乘進去、逐層加出來，避免重復乘法和冪展開。

---

?第一步：我們從最原始的泰勒公式出發

以 e^x?為例，泰勒展開是：

?

這表達得很清晰，每一項結構都類似：

• 分子是 x^k

• 分母是 k！

所以直覺上，我們就寫了：

double num = 1;  // 分子
double den = 1;  // 分母double taylor(int n, double x) {if (n == 0) return 1;               // 1?? 錨點：停止遞歸double res = taylor(n - 1, x);      // 2?? 先構造前面所有項的和num *= x;                           // 3?? 然后再更新狀態den *= n;return res + num / den;             // 4?? 當前項加進去
}

?遞歸方法的思路解析，可以看我之前發表的文章：

數據結構：遞歸：泰勒展開式（Taylor Series Expansion）-CSDN博客

?但是整個算法需要?O(n^2)?次的乘法。

于是我們問自己：

?有沒有一種辦法，我們不顯式地計算冪和階乘，而是用一種更聰明的方式重寫它？

第二步：從形式上重新觀察展開式?

我們把：

我們嘗試反向收斂：

從最后一項往前看。?

設：

假設我們已知最后一項是：

我們問：有沒有可能構造出一個結構：

?

我們知道這種結構是逐層“乘進去再加”，是一種“嵌套結構”。

這時候，你會自然聯想到：

---

🌟 第三步：引出霍納法則（Horner’s Rule）

Horner's Rule 是一種重寫多項式的方式，使其變成嵌套乘加結構，從而節省乘法次數。

給你一個多項式：

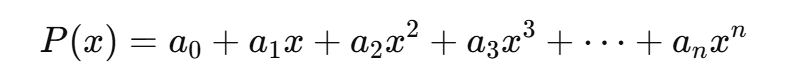
它可以等價重寫成：

?

第一步：從最后一項開始反向思考?

先寫出最后一項：

但我們不這么直接展開，而是嘗試合并每一項，構建嵌套結構。我們回顧一下：?

第二步：嘗試因式提取，構造嵌套結構?

我們從最后一項往回包，先只保留最后一項：

向前一項加：

?再加：

?最后加 1 項：

第三步：得出結論（形式）

最終你得到的就是：

?

這就是 Horner 法則在泰勒展開中的精確結構！?

?

---

?第四步：如何用這個結構重寫泰勒展開式？?

霍納法則告訴我們：

如果你有一個嵌套表達式，它從最深處開始乘加，就可以從最后一項反向累積計算。

我們的目標是以某種結構計算它，讓乘法次數最少。?

觀察這個嵌套結構你會發現：

• 每一層都包含一個 “1 + x / k * (之前的結果)”

• 最里面的是 1

• 然后不斷被 x/k 包裹

它是一個“逐層包裹”的結構，每一層是：

?這說明我們可以從“最深的那一層”開始往外展開。

于是你意識到這就是一種“右折疊（right fold）”，即：

result = 1;
result = 1 + x * result / 4;
result = 1 + x * result / 3;
result = 1 + x * result / 2;
result = 1 + x * result / 1;

?從后往前包，每次乘進去一個 x / i，再加 1。

所謂「右折疊」就是我們從表達式的最右邊開始構建，逐層包起來。?

1 + x/4              ← 第 1 層（最里面）
1 + x/3 * (1 + x/4)  ← 第 2 層
1 + x/2 * (...)      ← 第 3 層
1 + x/1 * (...)      ← 第 4 層

你看到一種非常明顯的重復：

每次的操作是：

result = 1 + x * result / i;

從哪個 i 開始？

• 最深一層是對應最大項 n

• 然后是 n - 1

• 最后是 i = 1

所以你會寫一個反向的循環：

for (int i = n; i > 0; --i)

初始值設置為：

double result = 1.0;  // 最里層的恒定值

為什么是 1.0？

因為你可以認為最內層就是 1 + 0，也就是我們從最后一項 x^n / n! 折疊得到的值是最深的那個 1，逐層向外構建。

完整代碼

double horner_taylor(int n, double x) {double result = 1.0;                  // 最深嵌套項for (; n > 0; n--) {                 // 從內往外迭代result = 1 + x * result / n;     // 每次構造一層}return result;
}

---

?從迭代轉換成遞歸邏輯

遞歸的本質是：

用一個函數在每一層調用自己，把循環變成函數調用鏈。

從上面的迭代式：

你可以直接轉換成遞歸表達式：

double horner_recursive(int n, double x) {static double result = 1.0;if (n == 0) return result;       // 最深嵌套項（base case）result = 1 + x / n * result;  return horner_recursive(n - 1, x);   
}

循環版結構	遞歸版結構
從 n 逐步降到 1	從 n 遞歸到 0（遞歸終止條件）
每次更新 result = ...	每次返回 1 + x * 下層 / n
初始 result = 1.0	horner_recursive(0, x) = 1.0

兩者實際上是完全等價的計算結構。

---

“迭代”和“循環”?

什么是“循環”（loop）？

• 循環是語法結構

• 是編程語言提供的控制流語句（for、while、do-while）

• 它的作用是：重復執行某段代碼

比如：

for (int i = 0; i < 10; ++i) {// 執行 10 次
}

什么是“迭代”（iteration）？

• 迭代是算法行為

• 意思是：基于前一個結果，不斷構造下一個結果

• 它不依賴一定要用循環語法，也可以用遞歸實現！

舉例說明：

? 迭代行為 + 循環實現

double result = 1;
for (int i = n; i > 0; --i)result = 1 + x * result / i;

• 每一輪基于上一輪的 result

• 所以這是一個迭代算法

• 同時用了 for，所以也是一個循環結構

?? 迭代行為 + 遞歸實現

double horner_recursive(int n, double x) {static double result = 1.0;if (n == 0) return result;       // 最深嵌套項（base case）result = 1 + x / n * result;  return horner_recursive(n - 1, x);   
}

• 每一層基于“下一層”的結果

• 所以也是一種迭代算法

• 但這次用的是遞歸結構

?🚫 循環 ≠ 迭代（反例）

for (int i = 0; i < 10; ++i) {cout << "Hello\n";
}

• 這使用了循環，但沒有迭代行為（沒有前后狀態依賴）

• 所以它是循環，但不是迭代