1. 堆(Heap)
1.1. Python實現堆的插入、堆頂刪除和排序
class MaxHeap:def __init__(self):# 初始化空堆,使用列表表示self.heap = []def insert(self, val):# 插入元素并執行上浮self.heap.append(val)self._sift_up(len(self.heap) - 1)def delete(self):# 刪除并返回堆頂元素if not self.heap:return Noneself._swap(0, len(self.heap) - 1)max_val = self.heap.pop()self._sift_down(0)return max_valdef build_heap(self, arr):# 從任意數組構建大頂堆self.heap = arr[:]for i in range((len(self.heap) - 2) // 2, -1, -1):self._sift_down(i)def heapsort(self):# 原地堆排序(不會額外開辟空間)n = len(self.heap)# 先構建堆for i in range((n - 2) // 2, -1, -1):self._sift_down(i)# 每次把最大值(堆頂)放到末尾,然后縮小堆范圍for end in range(n - 1, 0, -1):self._swap(0, end)self._sift_down(0, end)def _sift_up(self, idx):# 上浮操作,保持堆結構parent = (idx - 1) // 2while idx > 0 and self.heap[idx] > self.heap[parent]:self._swap(idx, parent)idx = parentparent = (idx - 1) // 2def _sift_down(self, idx, size=None):# 下沉操作,保持堆結構(可傳入范圍用于排序)if size is None:size = len(self.heap)while True:largest = idxleft = 2 * idx + 1right = 2 * idx + 2if left < size and self.heap[left] > self.heap[largest]:largest = leftif right < size and self.heap[right] > self.heap[largest]:largest = rightif largest == idx:breakself._swap(idx, largest)idx = largestdef _swap(self, i, j):# 輔助函數:交換堆中兩個元素self.heap[i], self.heap[j] = self.heap[j], self.heap[i]def __str__(self):# 返回堆內容的字符串表示return str(self.heap)import heapqdef heapsort_asc(iterable):heap = []for value in iterable:heapq.heappush(heap, value) # 構建最小堆return [heapq.heappop(heap) for _ in range(len(heap))] # 升序彈出# 示例
nums = [7, 2, 5, 3, 1]
print("升序堆排序結果:", heapsort_asc(nums))1.2. 堆的定義
1. 堆的基本概念
- 堆是一種特殊的樹形數據結構,廣泛應用于算法中,如堆排序。
- 堆的兩個主要特征:
- 完全二叉樹:除了最后一層,其他層的節點都已滿,最后一層的節點靠左排列。
- 節點值的大小關系:
????????大頂堆(Max-Heap):每個節點的值都大于或等于其子節點的值。
????????小頂堆(Min-Heap):每個節點的值都小于或等于其子節點的值。
2. 堆的實現與存儲
- 堆通常使用數組來存儲,因為完全二叉樹的結構適合用數組表示。
- 對于列表下標為
i的節點:
左子節點下標:2i + 1
右子節點下標:2i + 2
父節點下標:i -1 // 2

1.3. 堆的核心操作
完全二叉樹比較適合用數組來存儲。用數組來存儲完全二叉樹是非常節省存儲空間的。因為我們不需要存儲左右子節點的指針,單純地通過數組的下標,就可以找到一個節點的左右子節點和父節點。
具體python代碼見5.1,以大頂堆為例。
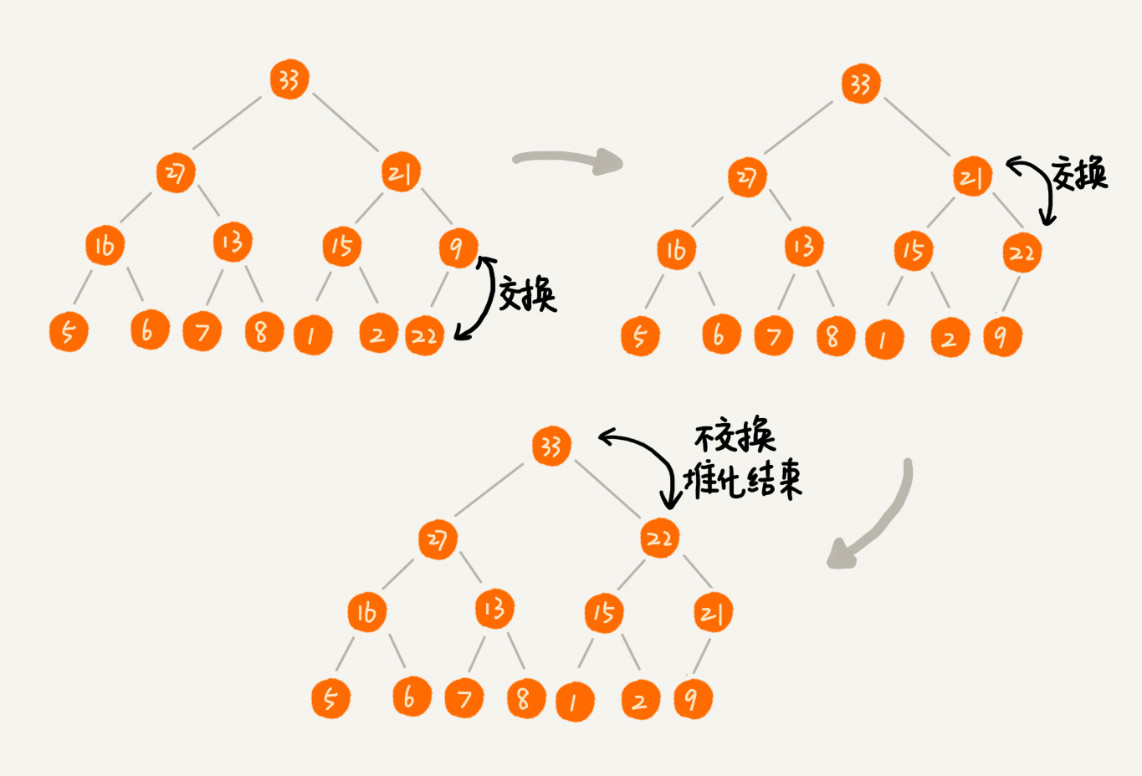
1. 往堆中插入一個元素
- 將新元素插入堆的最后,然后進行堆化(Heapify)操作來恢復堆的性質。
- 堆化分為兩種方式:
自下而上堆化:從插入的節點開始,依次與父節點比較,直到堆的性質恢復。
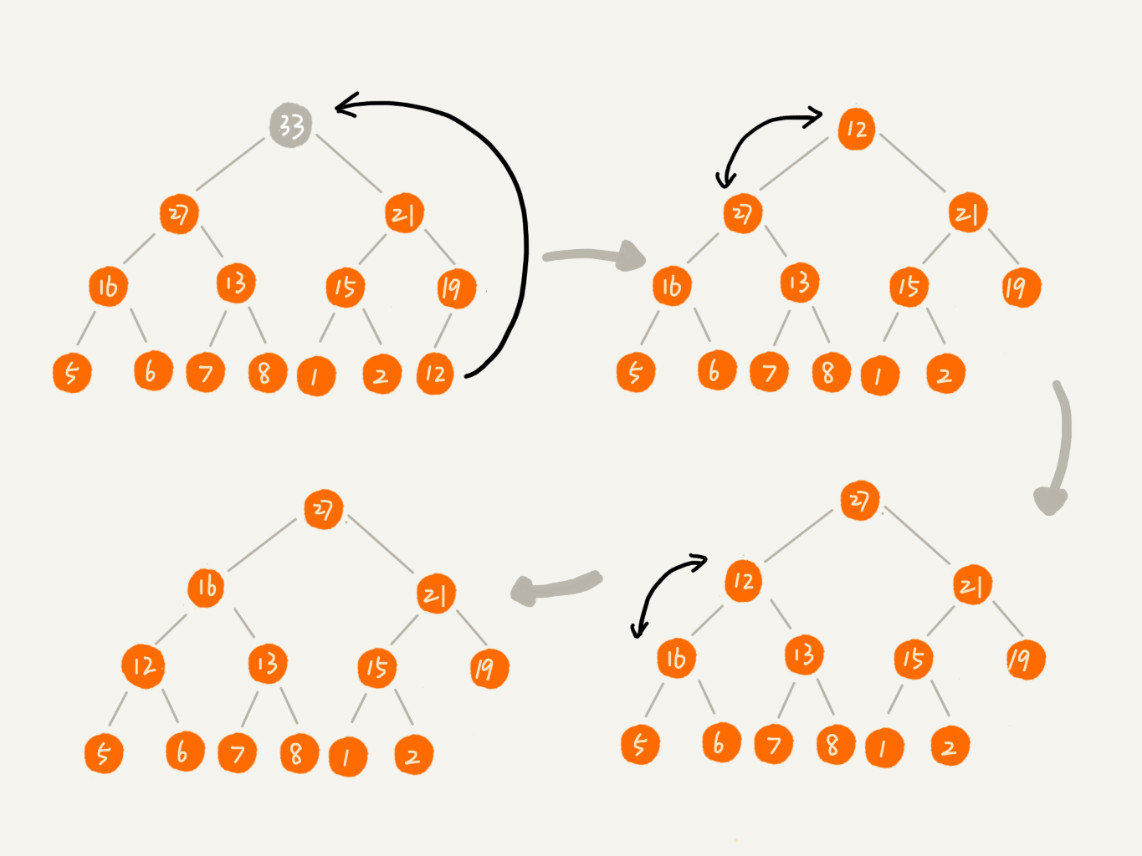
2. 刪除堆頂元素
刪除堆頂元素(最大或最小)后,將最后一個元素移動到堆頂,并進行自上而下堆化來恢復堆的性質。
時間復雜度:
一個包含 n個節點的完全二叉樹,樹的高度不會超過 log2n。堆化的過程是順著節點所在路徑比較交換的,所以堆化的時間復雜度跟樹的高度成正比,也就是 O(logn)。插入數據和刪除堆頂元素的主要邏輯就是堆化,所以,往堆中插入一個元素和刪除堆頂元素的時間復雜度都是 O(logn)。
3. 堆排序
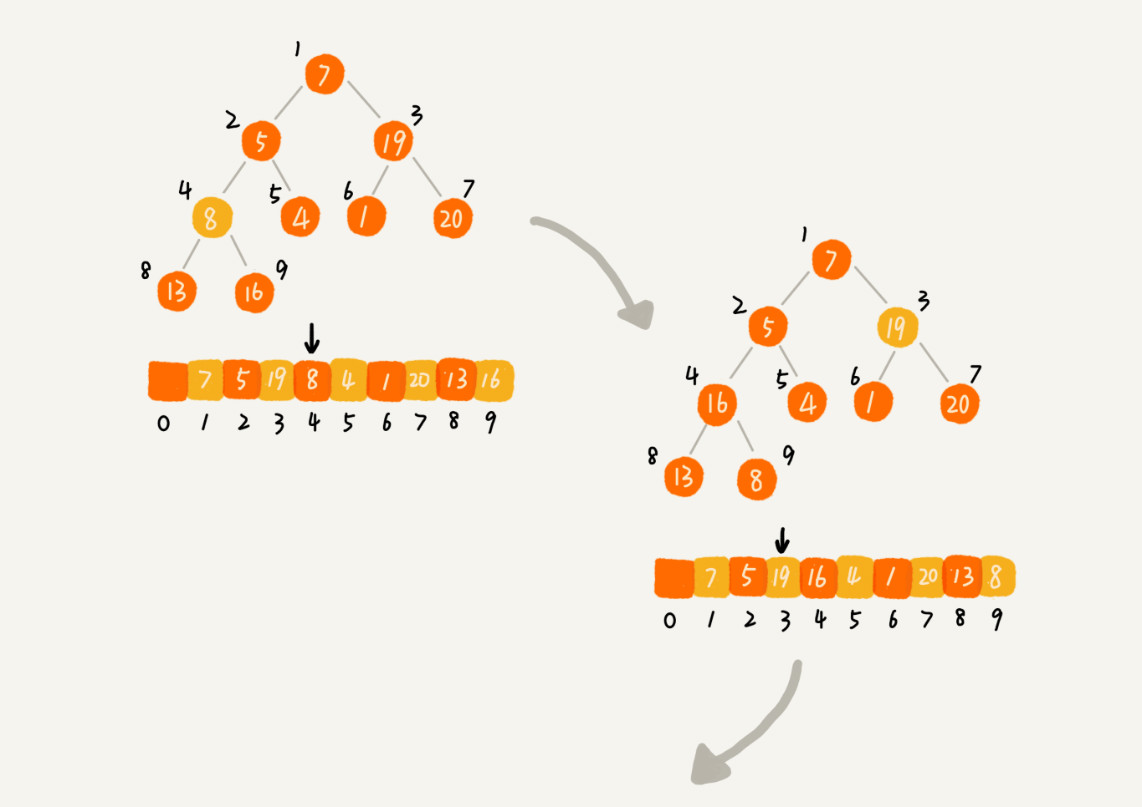
堆排序的過程大致分解成兩個大的步驟,建堆和排序。
建堆:
- 將數組構建成一個堆。
- 可以從前往后逐個插入元素構建堆(自下而上堆化)。
- 或者從后往前處理,使用自上而下堆化的方式來構建堆。

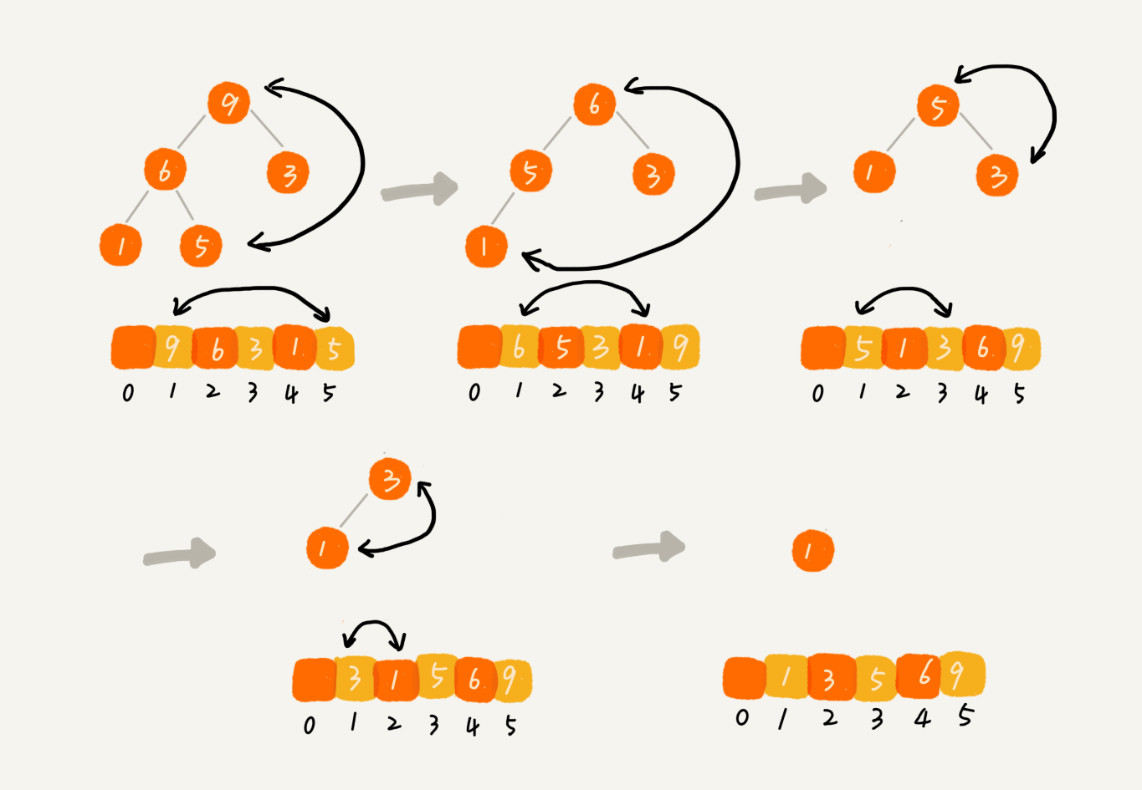
排序:
每次將堆頂元素(最大或最小)與最后一個元素交換,將堆的大小減小 1,然后進行堆化。重復此過程直到數組排序完成。
不是穩定的排序算法。
時間復雜度分析:
建堆:
雖然每個節點堆化的時間復雜度為 O(log n),但由于堆的層數遞減,因此建堆的時間復雜度是 O(n)。
排序:
每次刪除堆頂元素并堆化的時間復雜度為 O(log n),重復此過程 n 次,因此堆排序的總時間復雜度是 O(n log n)。
快速排序 vs 堆排序:性能對比表(實際開發視角)
| 對比維度 | 快速排序(Quick Sort) | 堆排序(Heap Sort) |
| 數據訪問模式 | 局部順序訪問:訪問相鄰元素,緩存友好 | 非順序訪問:跳躍式訪問(如下標 1 → 2 → 4 → 8),緩存不友好 |
| 緩存命中率 | 高(連續訪問內存,有利于 CPU 緩存預取) | 低(訪問分散,頻繁觸發緩存未命中) |
| 數據交換次數 | 相對較少,尤其在數據部分有序的情況下 | 多:建堆過程中頻繁打亂已有順序,導致額外的交換 |
| 對初始有序性敏感 | 是(部分有序時性能更好) | 否(建堆打亂順序) |
| 排序過程破壞有序度 | 否,盡量保持已有的順序結構 | 是,建堆導致已有順序被打亂 |
1.4. 堆的應用
1. 優先級隊列(Priority Queue)
定義:
- 與普通隊列不同,出隊順序按優先級高低而非 FIFO。
- 堆可高效實現優先級隊列:
????????????????插入元素:O(logn)
????????????????取出優先級最高元素(堆頂):O(logn)
應用示例:
合并有序小文件:
- 場景:將 100 個 100MB 的有序小文件合并為一個大文件。
- 方案:
????????每個文件取一個字符串放入小頂堆。
????????每次從堆頂取最小值寫入結果文件,再從對應文件中取下一個值加入堆。
????????時間復雜度大幅優于線性遍歷(數組)。
高性能定時器:
- 維護很多任務,每個任務有執行時間。
- 傳統方法每秒輪詢掃描任務表,低效。
- 使用小頂堆優化:
????????????????堆頂存放最早執行的任務。
????????????????定時器睡眠到該任務執行時間,節省資源。
????????????????每次取堆頂更新下一次喚醒時間。
2. 利用堆求 Top K 問題
Top K 分為兩類:
靜態 Top K(一次性獲取):
- 使用K 大小的小頂堆。
- 遍歷整個數組:
????????? ? ?若當前元素 > 堆頂:替換堆頂,重新堆化。
- 時間復雜度:
O(nlogK)
動態 Top K(實時查詢):
- 維護一個固定大小為 K 的小頂堆。
- 插入新數據時:
????????若新數據 > 堆頂:替換堆頂。
????????否則忽略。
- 查詢時直接返回堆中元素。
3. 利用堆求中位數(及任意百分位數據)
靜態數據集合:
- 可直接排序取中位數,代價高但結果固定。
動態數據集合:
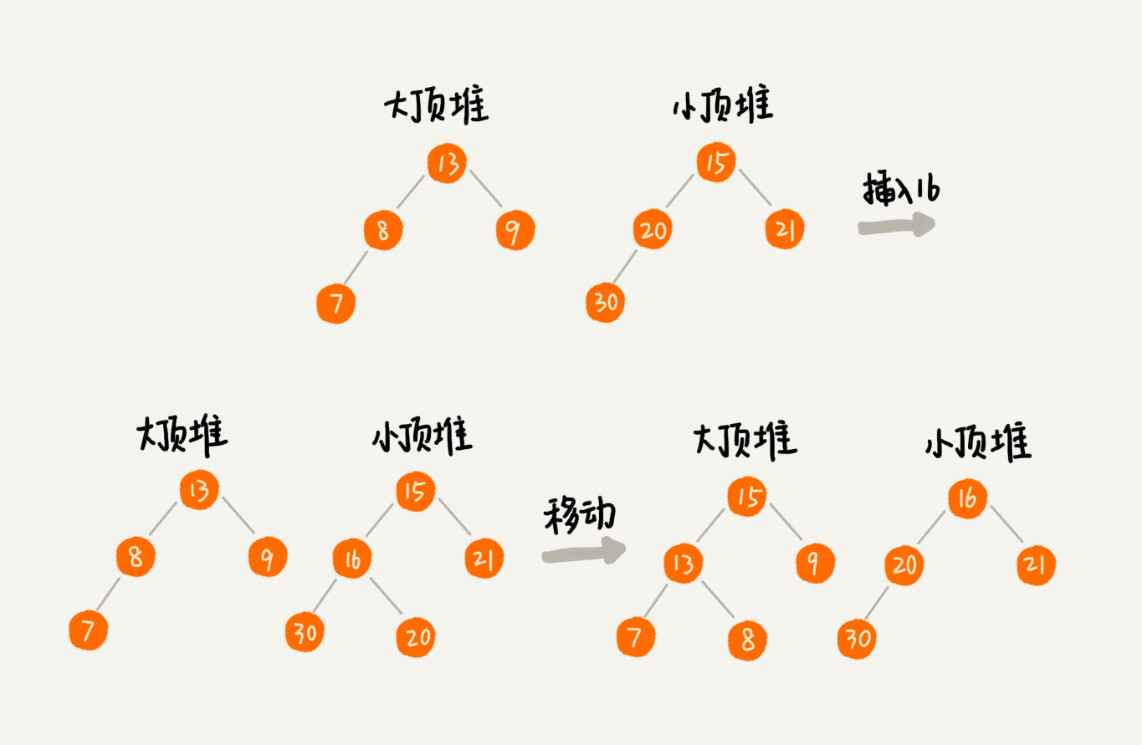
- 方法:雙堆法
????????大頂堆(max-heap):存前半部分數據。
????????小頂堆(min-heap):存后半部分數據,且小頂堆中的數據都大于大頂堆中的數據。
????????保持兩個堆平衡(大小相差不超過1)。
????????中位數取決于兩個堆的堆頂元素。
優勢:
- 每次插入數據后,只需調整兩個堆即可,效率高。
- 實現實時獲取中位數,時間復雜度約為
O(logn)。










)




-DA-02)



