字符串檢索算法：KMP和Trie樹

1.引言

2.KMP算法

3.Trie樹

3.1.簡介

3.2.Trie樹的應用場景

3.3.復雜度分析

3.4.Trie 樹的優缺點

3.5.示例

1.引言

????????字符串匹配，給定一個主串?S?和一個模式串?P，判斷?P?是否是?S?的子串，即找到?P?在?S?中第一次出現的位置。暴力匹配的思路是：從主串?S?的每個位置開始，逐個字符與模式串?P?比較。若匹配失敗，主串指針回退到起始位置的下一個位置，重新開始匹配。?時間復雜度：最壞情況下為?O(n×m)（n?為主串長度，m?為模式串長度）。缺陷：當模式串存在重復前綴或后綴時，重復比較了很多已知信息，效率低下。于是就引出了KMP算法。

2.KMP算法

? ? ? ? 要理解KMP算法，首先要搞清楚真前綴與真后綴。在一個字符串中，真前綴是指除了最后一個字符外，一個字符串的頭部連續的若干字符；真后綴是指除了第一個字符外，一個字符串的尾部連續的若干字符。舉個例子：

????????字符串："ABCDABD"

????????真前綴："A"、"AB"、"ABC"、"ABCD"、"ABCDA"、"ABCDAB"

????????真后綴："BCDABD"、"CDABD"、"DABD"、"ABD"、"BD"、"D"

遞推計算next數組

????????next 數組的求解基于“真前綴”和“真后綴”，即next[i]等于P[0]...P[i - 1]最長的相同真前后綴的長度（首先設置next[0]=-1,邊界條件）。我們以表格為例：

i	0	1	2	3	4	5	6	7
模式串	A	B	C	D	A	B	D	'\0'
next[ i ]	-1	0	0	0	0	1	2	0

i = 0，對于模式串的首字符，我們統一為next[0] = -1；
i = 1，前面的字符串為A，其最長相同真前后綴長度為 0，即next[1] = 0；
i = 2，前面的字符串為AB，其最長相同真前后綴長度為 0，即next[2] = 0；
i = 3，前面的字符串為ABC，其最長相同真前后綴長度為 0，即next[3] = 0；
i = 4，前面的字符串為ABCD，其最長相同真前后綴長度為 0，即next[4] = 0；
i = 5，前面的字符串為ABCDA，其最長相同真前后綴為A，即next[5] = 1；
i = 6，前面的字符串為ABCDAB，其最長相同真前后綴為AB，即next[6] = 2；
i = 7，前面的字符串為ABCDABD，其最長相同真前后綴長度為 0，即next[7] = 0。

????????那么，為什么根據最長相同真前后綴的長度就可以實現在不匹配情況下的跳轉呢？舉個代表性的例子：假如i = 6時不匹配，此時我們是知道其位置前的字符串為ABCDAB，仔細觀察這個字符串，首尾都有一個AB，既然在i = 6處的 D 不匹配，我們為何不直接把i = 2處的 C 拿過來繼續比較呢，因為都有一個AB啊，而這個AB就是ABCDAB的最長相同真前后綴，其長度 2 正好是跳轉的下標位置。

????????思路如此簡單，接下來就是代碼實現了，如下：

// 生成Next數組, 示例：“GTGTGCF”
std::vector<int> buildNext(const std::string& pattern) {std::vector<int> next(pattern.size(), 0);int j = 0;for (int i = 2; i < pattern.length(); i++) {while (j != 0 && pattern[j] != pattern[i - 1]) {//從next[i+1]的求解回溯到 next[j]j = next[j];}if (pattern[j] == pattern[i - 1]) {j++;}next[i] = j;}return next;
}

int kmpSearch(const std::string& text, const std::string& pattern) {//預處理，生成next數組std::vector<int> next(std::move(buildNext(pattern)));int j = 0;//主循環，遍歷主串字符for (int i = 0; i < text.length(); i++) {while (j > 0 && text[i] != pattern[j]) {//遇到壞字符時，查詢next數組并改變模式串的起點j = next[j];}if (text[i] == pattern[j]) {j++;}if (j == pattern.length()) {//匹配成功，返回下標return i - pattern.length() + 1;}}return  -1;
}

復雜度分析：

時間復雜度：
- 構建?next?數組：O(m)（每個字符最多被訪問兩次）。
- 匹配過程：O(n)（主串指針?i?僅遞增，不回退）。
- 總復雜度：O(n+m)，優于暴力匹配的?O(n×m)。
空間復雜度：O(m)（存儲?next?數組）。

3.Trie樹

3.1.簡介

????????Trie樹，即前綴樹，又稱單詞查找樹，字典樹，是一種樹形結構，是一種哈希樹的變種。典型應用是用于統計和排序大量的字符串（但不僅限于字符串），所以經常被搜索引擎系統用于文本詞頻統計。

??Trie樹的核心思想是空間換時間，利用字符串的公共前綴來降低查詢時間的開銷以達到提高效率的目的。它的優點是：最大限度地減少無謂的字符串比較，查詢效率比哈希表高。

它有3個基本性質：

根節點不包含字符，除根節點外每一個節點都只包含一個字符。
從根節點到某一節點，路徑上經過的字符連接起來，為該節點對應的字符串。
每個節點的所有子節點包含的字符都不相同。

舉一個例子。給出一組單詞，inn, int, at, age, adv, ant, 我們可以得到下面的Trie：

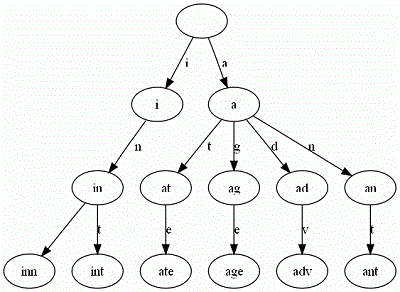
3.2.Trie樹的應用場景

字符串檢索，詞頻統計，搜索引擎的熱門查詢

? ? ? ? trie樹在大數據查找和檢索方面具有獨特的優勢，不過就是要求內存比較高，不過在沒有內存限制的情況不適為一種好的方式，如：(節選自此文：海量數據處理面試題集錦與Bit-map詳解)

a）有一個1G大小的一個文件，里面每一行是一個詞，詞的大小不超過16字節，內存限制大小是1M。返回頻數最高的100個詞。

b）?1000萬字符串，其中有些是重復的，需要把重復的全部去掉，保留沒有重復的字符串。請怎么設計和實現？

c）尋找熱門查詢：搜索引擎會通過日志文件把用戶每次檢索使用的所有檢索串都記錄下來，每個查詢串的長度為1-255字節。假設目前有一千萬個記錄，這些查詢串的重復讀比較高，雖然總數是1千萬，但是如果去除重復和，不超過3百萬個。一個查詢串的重復度越高，說明查詢它的用戶越多，也就越熱門。請你統計最熱門的10個查詢串，要求使用的內存不能超過1G。

d）一個文本文件，大約有一萬行，每行一個詞，要求統計出其中最頻繁出現的前10個詞，請給出思想，給出時間復雜度分析

e)?給出一個詞典，其中的單詞為不良單詞。單詞均為小寫字母。再給出一段文本，文本的每一行也由小寫字母構成。判斷文本中是否含有任何不良單詞。例如，若rob是不良單詞，那么文本problem含有不良單詞。

(1) 請描述你解決這個問題的思路；
(2) 請給出主要的處理流程，算法，以及算法的復雜度。

字符串最長公共前綴

????????Trie樹利用多個字符串的公共前綴來節省存儲空間，反之，當我們把大量字符串存儲到一棵trie樹上時，我們可以快速得到某些字符串的公共前綴。舉例：

? ? ? 給出N 個小寫英文字母串，以及Q 個詢問，即詢問某兩個串的最長公共前綴的長度是多少. ?解決方案：

? ? ? ? 首先對所有的串建立其對應的字母樹。此時發現，對于兩個串的最長公共前綴的長度即它們所在結點的公共祖先個數，于是，問題就轉化為了離線 ?（Offline）的最近公共祖先（Least Common Ancestor，簡稱LCA）問題。

? ? ? ?而最近公共祖先問題同樣是一個經典問題，可以用下面幾種方法：

? ? ? ? 1.?利用并查集（Disjoint Set），可以采用采用經典的Tarjan 算法；

? ? ? ? 2. 求出字母樹的歐拉序列（Euler Sequence ）后，就可以轉為經典的最小值查詢（Range Minimum Query，簡稱RMQ）問題了；

3.3.復雜度分析

插入操作：時間復雜度為 O (m)，這里的 m 指的是字符串的長度。
查找操作：時間復雜度同樣為 O (m)。
空間復雜度：空間復雜度為 O (n)，n 表示所有字符串中不同字符的總數，這一特點使得 Trie 樹在處理大量字符串時非常高效。

3.4.Trie 樹的優缺點

優點

高效前綴匹配：快速查找所有以某前綴開頭的字符串（如搜索提示）。
避免重復存儲：共享公共前綴，節省空間。
時間復雜度穩定：插入、查詢、刪除的時間復雜度均為?O(n)（n 為字符串長度）。

缺點

空間開銷大：每個字符占用一個節點，可能浪費內存（尤其是字符集大時）。
實現復雜：需要處理動態節點分配和指針操作。

3.5.示例

示例一：一個字符串類型的數組arr1，另一個字符串類型的數組arr2。

arr2中有哪些字符串，是arr1中出現的？請打印
arr2中有哪些字符串，是作為arr1中某個字符串前綴出現的？請打印
arr2中有哪些字符串，是作為arr1中某個字符串前綴出現的？請打印arr2中出現次數最大的前綴。

實現代碼如下：

#include <iostream>
#include <string>
#include <string.h>using namespace std;
const int MaxBranchNum = 26;//可以擴展class TrieNode{
public:string word;int path;  //該字符被劃過多少次，用以統計以該字符串作為前綴的字符串的個數int End; //以該字符結尾的字符串TrieNode* nexts[MaxBranchNum];TrieNode(){word = "";path = 0;End = 0;memset(nexts,NULL,sizeof(TrieNode*) * MaxBranchNum);}};class TrieTree{
private:TrieNode *root;
public:TrieTree();~TrieTree();//插入字符串strvoid insert(string str);//查詢字符串str是否出現過，并返回作為前綴幾次int search(string str);//刪除字符串strvoid Delete(string str);void destory(TrieNode* root);//打印樹中的所有節點void printAll();//打印以str作為前綴的單詞void printPre(string str);//按照字典順序輸出以root為根的所有單詞void Print(TrieNode* root);//返回以str為前綴的單詞的個數int prefixNumbers(string str);
};TrieTree::TrieTree()
{root = new TrieNode();
}TrieTree::~TrieTree()
{destory(root);
}void TrieTree::destory(TrieNode* root)
{if(root == nullptr)return ;for(int i=0;i<MaxBranchNum;i++){destory(root->nexts[i]);}delete root;root = nullptr;
}void TrieTree::insert(string str)
{if(str == "")return ;char buf[str.size()];strcpy(buf, str.c_str());TrieNode* node = root;int index = 0;for(int i=0; i<strlen(buf); i++){index = buf[i] - 'a';if(node->nexts[index] == nullptr){node->nexts[index] = new TrieNode();}node = node->nexts[index];node->path++;//有一條路徑劃過這個節點}node->End++;node->word = str;
}int TrieTree::search(string str)
{if(str == "")return 0;char buf[str.size()];strcpy(buf, str.c_str());TrieNode* node = root;int index = 0;for(int i=0;i<strlen(buf);i++){index = buf[i] - 'a';if(node->nexts[index] == nullptr){return 0;}node = node->nexts[index];}if(node != nullptr){return node->End;}else{return 0;}
}void TrieTree::Delete(string str)
{if(str == "")return ;char buf[str.size()];strcpy(buf, str.c_str());TrieNode* node = root;TrieNode* tmp;int index = 0;for(int i = 0 ; i<str.size();i++){index = buf[i] - 'a';tmp = node->nexts[index];if(--node->nexts[index]->path == 0){delete node->nexts[index];}node = tmp;}node->End--;
}int TrieTree::prefixNumbers(string str)
{if(str == "")return 0;char buf[str.size()];strcpy(buf, str.c_str());TrieNode* node = root;int index = 0;for(int i=0;i<strlen(buf);i++){index = buf[i] - 'a';if(node->nexts[index] == nullptr){return 0;}node = node->nexts[index];}return node->path;
}
void TrieTree::printPre(string str)
{if(str == "")return ;char buf[str.size()];strcpy(buf, str.c_str());TrieNode* node = root;int index = 0;for(int i=0;i<strlen(buf);i++){index = buf[i] - 'a';if(node->nexts[index] == nullptr){return ;}node = node->nexts[index];}Print(node);
}void TrieTree::Print(TrieNode* node)
{if(node == nullptr)return ;if(node->word != ""){cout<<node->word<<" "<<node->path<<endl;}for(int i = 0;i<MaxBranchNum;i++){Print(node->nexts[i]);}
}void TrieTree::printAll()
{Print(root);
}int main()
{cout << "Hello world!" << endl;TrieTree trie;string str = "li";cout<<trie.search(str)<<endl;trie.insert(str);cout<<trie.search(str)<<endl;trie.Delete(str);cout<<trie.search(str)<<endl;trie.insert(str);cout<<trie.search(str)<<endl;trie.insert(str);cout<<trie.search(str)<<endl;trie.Delete("li");cout<<trie.search(str)<<endl;trie.Delete("li");cout<<trie.search(str)<<endl;trie.insert("lia");trie.insert("lic");trie.insert("liab");trie.insert("liad");trie.Delete("lia");cout<<trie.search("lia")<<endl;cout<<trie.prefixNumbers("lia")<<endl;return 0;
}

示例二：實現?Trie 樹，包含插入、查找、前綴搜索和刪除功能。這個實現使用智能指針管理內存，確保內存安全。代碼如下：

#include <iostream>
#include <memory>
#include <string>
#include <unordered_map>class TrieNode {
public:std::unordered_map<char, std::unique_ptr<TrieNode>> children;bool is_end_of_word;TrieNode() : is_end_of_word(false) {}
};class Trie {
private:std::unique_ptr<TrieNode> root;// 輔助函數：遞歸刪除單詞bool remove(TrieNode* current, const std::string& word, int index) {if (index == word.length()) {if (!current->is_end_of_word)return false;current->is_end_of_word = false;return current->children.empty();}char ch = word[index];auto it = current->children.find(ch);if (it == current->children.end())return false;bool shouldDeleteCurrentNode = remove(it->second.get(), word, index + 1) && !it->second->is_end_of_word;if (shouldDeleteCurrentNode) {current->children.erase(ch);return current->children.empty();}return false;}public:Trie() : root(std::make_unique<TrieNode>()) {}// 插入單詞void insert(const std::string& word) {TrieNode* current = root.get();for (char ch : word) {if (!current->children.count(ch)) {current->children[ch] = std::make_unique<TrieNode>();}current = current->children[ch].get();}current->is_end_of_word = true;}// 查找單詞bool search(const std::string& word) const {const TrieNode* current = root.get();for (char ch : word) {auto it = current->children.find(ch);if (it == current->children.end())return false;current = it->second.get();}return current->is_end_of_word;}// 查找前綴bool startsWith(const std::string& prefix) const {const TrieNode* current = root.get();for (char ch : prefix) {auto it = current->children.find(ch);if (it == current->children.end())return false;current = it->second.get();}return true;}// 刪除單詞void deleteWord(const std::string& word) {remove(root.get(), word, 0);}
};// 使用示例
int main() {Trie trie;trie.insert("apple");std::cout << std::boolalpha;std::cout << trie.search("apple") << std::endl;   // 輸出: truestd::cout << trie.search("app") << std::endl;     // 輸出: falsestd::cout << trie.startsWith("app") << std::endl; // 輸出: truetrie.insert("app");std::cout << trie.search("app") << std::endl;     // 輸出: truetrie.deleteWord("apple");std::cout << trie.search("apple") << std::endl;   // 輸出: falsestd::cout << trie.search("app") << std::endl;     // 輸出: truereturn 0;
}

這個 C++ 實現具有以下特點：