shiyonguyu大家好，我是我不是小upper！最近行業大環境不是很好，有人苦惱別人都開始著手項目實戰了，自己卻還卡在 scikit-learn 的代碼語法上，連簡單的示例運行起來都磕磕絆絆。確實，對很多機器學習初學者來說，一邊要啃算法原理，一邊得熟悉代碼操作，后面還要接觸大數據相關知識，每一步都不容易。這也恰恰解釋了為什么算法工程師的薪資和待遇普遍比較可觀 —— 掌握這些技能需要下不少功夫。

既然大家在 scikit-learn 的學習上遇到困難，接下來這段時間，我就專門和大家嘮嘮這個工具的使用方法。今天先從監督學習部分入手，其他內容后續也會陸續分享。這篇干貨滿滿，建議先收藏，方便隨時拿出來學習！

---

優缺點

在大家的日常生活中，無論是工作還是學習，scikit-learn都占有舉足輕重的地位！咱先聊聊它的優缺點，讓大家有一個整體的認識！

優點：

1、簡單易用：scikit-learn提供了一種簡單而一致的API，使用戶能夠輕松地訓練、評估和部署各種監督學習模型。

2、豐富的文檔和示例：詳盡的文檔和示例，以幫助用戶理解算法和如何使用它們，這降低了學習曲線。

3、廣泛的算法支持：包括多種監督學習算法，從傳統的線性模型到集成方法和深度學習，滿足了各種問題的需求。

4、開源社區支持：強大的開源社區，用戶可以獲得支持、反饋和貢獻新功能和改進。

5、性能優化：庫中的算法通常經過高度優化，以提供高性能的計算，特別是在大規模數據集上。

6、數據預處理工具：包括數據預處理、特征工程和特征選擇工具，有助于準備和處理數據。

7、交叉驗證和模型選擇：提供了交叉驗證和模型選擇工具，有助于選擇最佳模型參數，避免過擬合。

8、可擴展性：用戶可以輕松地擴展庫，自定義評估器、轉換器和度量。

缺點：

1、有些算法的性能：盡管scikit-learn包括廣泛的算法，但某些特殊問題可能需要更專業的庫或深度學習框架來實現最佳性能。

2、深度學習支持限制：雖然scikit-learn包括MLP（多層感知機）等神經網絡模型，但對于深度學習任務，深度學習框架如TensorFlow和PyTorch可能更適合。

3、自動特征工程：自動特征工程工具有限，復雜的特征工程任務可能需要其他庫或手動處理。

4、處理大規模數據集的能力：對于大規模數據集，scikit-learn的性能和內存管理可能存在挑戰。

5、不支持序列數據：對于時序數據或自然語言處理任務，需要額外的庫和工具。

有了一個整體的認識之后，專門針對監督學習算法，各個舉例，給出大家完整可以拋出結果的代碼示例來。

• 線性回歸

• 邏輯回歸

• 支持向量機

• 決策樹和隨機森林

• K-Means

• 集成方法

• 高斯混合模型

• 梯度提升樹

• AdaBoost

• 神經網絡

老規矩：大家伙如果覺得近期文章還不錯！歡迎大家點贊、轉發安排起來，讓更多的朋友看到。

---

線性回歸

線性回歸的核心目標，是找到一條能最準確描述自變量和因變量之間關系的直線。簡單來說，就是通過不斷縮小實際數據和預測數據之間的誤差，來確定這條最佳的擬合線，進而預測目標變量的值。比如在房價預測場景中，我們想知道房屋的某個特征（像房間數量）和房價之間存在怎樣的線性關系，這就是線性回歸可以解決的問題。

接下來，我們通過一個波士頓房價預測的案例，詳細展示線性回歸的完整實現流程，整個過程包括數據準備、模型構建、訓練、預測、評估以及可視化六個關鍵步驟。

1. 導入必要的庫

在開始編寫代碼之前，我們需要先導入一些重要的工具庫。

• numpy：強大的數值計算庫，用于處理各種數據運算。
• matplotlib.pyplot：繪圖庫，能幫我們將數據和模型結果以可視化的形式展示出來，方便直觀理解。
• sklearn?相關模塊：sklearn?是機器學習領域常用的庫，其中?datasets?模塊用來加載公開數據集；linear_model?里的?LinearRegression?用于構建線性回歸模型；model_selection?中的?train_test_split?負責將數據集拆分為訓練集和測試集；metrics?模塊里的?mean_squared_error?和?r2_score?則用于評估模型的性能。

具體代碼如下：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

2. 加載和準備數據

我們使用經典的波士頓房價數據集，這個數據集包含了房屋的多種特征以及對應的房價信息。為了簡化演示過程，這里我們只選取 “平均房間數” 這一個特征作為自變量，來預測房屋價格（因變量）。

# 加載波士頓房價數據集
boston = datasets.load_boston()
# 準備數據，選取房間數作為特征
X = boston.data[:, np.newaxis, 5]
# 目標變量，即房屋價格
y = boston.target

3. 劃分數據集

為了準確評估模型在新數據上的表現，我們需要把數據集分成兩部分：一部分用于訓練模型，讓模型學習特征和目標變量之間的關系；另一部分用于測試模型，檢驗模型的泛化能力。

這里我們將數據集的 80% 作為訓練集，20% 作為測試集，并且設置?random_state=42，這樣可以保證每次運行代碼時，數據集的劃分結果都是一樣的，方便對比和調試。

# 劃分訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

4. 構建和訓練模型

接下來，我們創建一個線性回歸模型對象，并使用訓練集數據對其進行訓練。訓練的過程，就是模型根據給定的特征和目標值，不斷調整自身參數，尋找最佳擬合線的過程。

# 構建線性回歸模型
model = LinearRegression()
# 訓練模型
model.fit(X_train, y_train)

5. 進行預測

模型訓練好之后，我們就可以用它來對測試集中的數據進行預測，得到每個樣本對應的預測房價。

# 進行預測
y_pred = model.predict(X_test)

6. 評估模型性能

為了衡量模型預測的準確性，我們使用兩個常用的評估指標：

• 均方誤差（MSE）：計算預測值和實際值之間差值的平方的平均值，MSE 值越小，說明模型的預測越準確。
• 決定系數（R2）：用于評估模型對數據的擬合程度，取值范圍在 0 到 1 之間，越接近 1 表示模型擬合效果越好。

# 評估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

7. 可視化結果

最后，我們通過繪圖的方式，直觀展示模型的擬合效果。將測試集中的實際數據點繪制出來，再把模型預測的擬合線畫在同一圖中，這樣就能清晰地看到模型預測值和實際值的差異。

# 可視化結果
plt.scatter(X_test, y_test, color='black', label='實際數據')
plt.plot(X_test, y_pred, color='blue', linewidth=3, label='線性回歸擬合')
plt.title('線性回歸預測房價')
plt.xlabel('平均房間數')
plt.ylabel('房屋價格')
plt.legend()
plt.show()

運行完代碼后，我們還可以打印出評估指標的具體數值，進一步了解模型的性能表現：

print(f"均方誤差(Mean Squared Error): {mse:.2f}")
print(f"決定系數(R^2): {r2:.2f}")

---

邏輯回歸

通過 Scikit - Learn 中的 Iris 數據集進行一個具體的二元分類實踐。

邏輯回歸雖然名字里有 “回歸”，但它主要用于解決分類問題。它的核心是找到一個決策邊界，把不同類別的數據點區分開來。就像在一個大廣場上畫一條線，讓不同陣營的人分別站在線的兩邊。

1. 導入必要的庫

在開始代碼編寫之前，我們得先把要用的工具準備好，也就是導入相關的庫：

• numpy：它在處理數值計算方面超厲害，能幫我們高效地操作和處理數據。
• matplotlib.pyplot：這個庫主要用來繪圖。通過它，我們可以把數據和模型的結果用圖形展示出來，這樣就能更直觀地理解。
• sklearn?相關模塊：sklearn?是機器學習領域特別常用的庫。這里面的?datasets?模塊可以幫我們加載公開的數據集，像我們要用的 Iris 數據集就靠它；linear_model?里的?LogisticRegression?就是我們構建邏輯回歸模型要用到的類。

具體導入代碼如下：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import LogisticRegression

2. 加載和處理 Iris 數據集

Iris 數據集包含了三種不同種類鳶尾花的測量數據。為了方便后續可視化，我們只選擇其中兩個特征，也就是萼片長度和萼片寬度。同時，我們把原本多分類的標簽轉化成一個二元分類問題，規定其中一種鳶尾花對應的標簽為 0，另一種為 1 。

代碼實現是這樣的：

# 加載Iris數據集
iris = datasets.load_iris()
# 僅使用前兩個特征（萼片長度和萼片寬度），方便可視化
X = iris.data[:, :2]
# 將標簽轉換為二進制分類問題，不是0類的就標記為1
y = (iris.target != 0) * 1 

3. 構建和訓練邏輯回歸模型

接下來，我們要創建一個邏輯回歸模型對象。這里我們指定了求解器為?liblinear，它適用于小規模數據集，能比較高效地找到模型的最優參數。然后，我們用準備好的數據集對模型進行訓練，讓模型學習數據中蘊含的規律，找到能區分兩類鳶尾花的決策邊界。

代碼如下：

# 構建邏輯回歸模型
model = LogisticRegression(solver='liblinear')
# 訓練模型
model.fit(X, y)

4. 繪制決策邊界圖

模型訓練好之后，我們想看看它找到的決策邊界長啥樣，以及數據點在這個邊界兩邊是怎么分布的，這就需要繪制決策邊界圖。
我們先確定繪圖區域的范圍，也就是找到特征數據在兩個維度上的最小值和最大值，然后向外擴展一點，保證能把所有數據點都包含進去。接著，我們創建一個網格，這個網格就像是在繪圖區域鋪上了密密麻麻的小方格。對于網格中的每個點，我們用訓練好的模型去預測它屬于哪一類，得到預測結果后，把這些結果按照網格的形狀重新排列。最后，我們把決策邊界和數據點都畫出來。

具體代碼如下：

# 確定繪圖區域范圍
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
# 創建網格
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
# 對網格中的點進行預測
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolor='k')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('LogisticRegression')
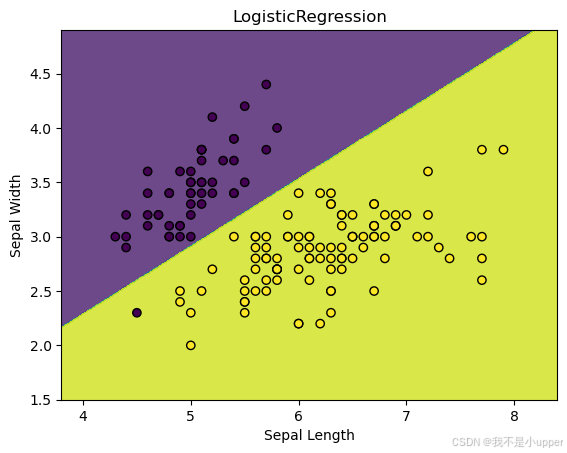
plt.show()

運行這段代碼，我們就能看到邏輯回歸模型找到的那條分隔兩種鳶尾花的決策邊界，以及數據點在邊界兩側的分布情況。下圖很好地展示了邏輯回歸用于二元分類問題的關鍵概念，也就是如何通過找到合適的決策邊界來區分不同類別的數據。希望大家通過這個例子，能對邏輯回歸有更深入的理解！

---

支持向量機在新穎性檢測中的應用

在實際的數據處理場景中，新穎性檢測是一項非常重要的任務，它能夠幫助我們識別出數據中的異常情況。下面，我們將使用 Scikit - Learn 中的支持向量機（SVM）模型來完成一個新穎性檢測的案例。這個案例會詳細展示從準備數據、構建模型到可視化結果的整個過程，讓大家更清晰地理解支持向量機在新穎性檢測中的工作原理。

1. 導入必要的庫

在開始之前，我們需要導入一些必要的 Python 庫，這些庫將幫助我們完成數據生成、模型構建和結果可視化等任務。

import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm

這里，numpy?庫用于進行數值計算和數據生成，matplotlib.pyplot?庫用于繪制圖形，sklearn?中的?svm?模塊則提供了支持向量機模型。

2. 生成合成數據集

為了演示新穎性檢測，我們需要創建一個包含正常觀測和異常觀測的合成數據集。我們使用?numpy?的隨機數生成功能來完成這個任務。

# 設置隨機數種子，保證結果可復現
np.random.seed(0)
# 生成訓練集中的正常觀測數據
X = 0.3 * np.random.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
# 生成測試集中的正常觀測數據
X = 0.3 * np.random.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
# 生成異常觀測數據
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))

在這段代碼中，我們首先設置了隨機數種子，這樣每次運行代碼時生成的數據都是一樣的，方便結果的復現。然后，我們通過?np.random.randn?函數生成符合正態分布的隨機數，構建訓練集和測試集中的正常觀測數據。最后，使用?np.random.uniform?函數生成均勻分布的隨機數作為異常觀測數據。

3. 構建支持向量機模型

接下來，我們使用?sklearn?中的?OneClassSVM?模型進行新穎性檢測。OneClassSVM?是一種無監督學習模型，它只需要正常數據作為輸入，然后學習正常數據的分布特征，從而識別出異常數據。

# 構建支持向量機模型
clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1)
# 使用訓練數據擬合模型
clf.fit(X_train)

在創建模型時，我們設置了一些參數。nu?表示異常數據在整個數據集中所占的比例上限，kernel?選擇了徑向基函數（RBF）作為核函數，gamma?是核函數的系數，它會影響模型的復雜度和泛化能力。然后，我們使用訓練數據?X_train?對模型進行訓練。

4. 進行預測并統計錯誤數量

模型訓練好后，我們使用它對訓練數據、測試數據和異常數據進行預測，并統計預測錯誤的數量。

# 對訓練數據進行預測
y_pred_train = clf.predict(X_train)
# 對測試數據進行預測
y_pred_test = clf.predict(X_test)
# 對異常數據進行預測
y_pred_outliers = clf.predict(X_outliers)# 統計訓練數據中的預測錯誤數量
n_error_train = y_pred_train[y_pred_train == -1].size
# 統計測試數據中的預測錯誤數量
n_error_test = y_pred_test[y_pred_test == -1].size
# 統計異常數據中的預測錯誤數量
n_error_outliers = y_pred_outliers[y_pred_outliers == 1].size

在?OneClassSVM?模型中，預測結果為 1 表示正常數據，-1 表示異常數據。我們通過比較預測結果和實際情況，統計出不同數據集上的預測錯誤數量。

5. 可視化結果

為了更直觀地展示支持向量機模型的工作效果，我們使用?matplotlib?庫繪制圖形。

# 創建網格點
xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
# 計算網格點到決策邊界的距離
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)# 設置圖形標題
plt.title("Novelty Detection")
# 繪制決策邊界以下的區域
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu)
# 繪制決策邊界
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors="darkred")
# 繪制決策邊界以上的區域
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors="palevioletred")# 設置散點大小
s = 40
# 繪制訓練數據點
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c="white", s=s, edgecolors="k")
# 繪制測試數據點
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c="blueviolet", s=s, edgecolors="k")
# 繪制異常數據點
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c="gold", s=s, edgecolors="k")
# 設置坐標軸范圍
plt.axis("tight")
plt.xlim((-5, 5))
plt.ylim((-5, 5))
# 添加圖例
plt.legend([a.collections[0], b1, b2, c],["Learned Frontier","Training Observations","New Regular Observations","New Abnormal Observations",],loc="upper left",prop=plt.matplotlib.font_manager.FontProperties(size=11),
)
# 添加x軸標簽，顯示預測錯誤數量
plt.xlabel("Train Errors: %d/200 ; Novel Regular Errors: %d/40 ; Novel Abnormal Errors: %d/40"% (n_error_train, n_error_test, n_error_outliers)
)
# 顯示圖形
plt.show()

我們創建了一個包含正常觀測和異常觀測的合成數據集，并使用?OneClassSVM?模型進行新穎性檢測。模型通過學習正常數據的分布特征，找到了一個決策邊界，將正常觀測和異常觀測分開。通過可視化結果，我們可以清晰地看到支持向量機是如何找到這個學習邊界的，這也充分演示了支持向量機在異常檢測問題中的應用。大家可以根據自己的需求調整模型的參數，進一步優化模型的性能。

---

決策樹與隨機森林

在機器學習領域，決策樹和隨機森林是兩種非常重要且常用的分類模型。今天，我們通過一個具體的案例，使用 Scikit - Learn 中的 Iris 數據集，來深入了解這兩種模型的工作原理，并通過可視化它們的決策邊界，直觀感受它們是如何對數據進行分類的。

1. 導入必要的庫

在開始編寫代碼之前，我們要先把需要用到的庫導入進來。這些庫就像是我們進行機器學習實驗的工具包，能幫助我們完成數據加載、模型訓練、結果可視化等一系列操作。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier

這里，matplotlib.pyplot?用于繪制圖形，numpy?用于數值計算，load_iris?函數可以幫我們加載 Iris 數據集，DecisionBoundaryDisplay?用于可視化模型的決策邊界，DecisionTreeClassifier?是決策樹模型的類，RandomForestClassifier?則是隨機森林模型的類。

2. 加載 Iris 數據集

Iris 數據集是一個非常經典的機器學習數據集，它包含了三種不同種類鳶尾花的多種特征數據以及對應的類別標簽。我們通過下面的代碼來加載這個數據集：

iris = load_iris()

加載完成后，iris?這個變量就包含了所有的花的特征數據和類別信息，我們后續的模型訓練和分析都將基于這些數據。

3. 設置一些參數

在進行模型訓練和可視化之前，我們先設置一些參數，方便后續的操作和圖形展示。

n_classes = 3
plot_colors = "ryb"
plot_step = 0.02

n_classes?表示 Iris 數據集中花的類別數量，這里是 3 種。plot_colors?定義了用于繪制不同類別數據點的顏色，分別對應紅（r）、黃（y）、藍（b）三種顏色。plot_step?是在繪制決策邊界時，網格點之間的間隔大小。

4. 創建圖形并劃分區域

為了同時展示不同特征組合下決策樹和隨機森林模型的決策邊界，我們創建一個包含 2x2 子圖的圖形。

fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)

這樣，我們就有了 4 個小的繪圖區域，可以分別用來繪制不同特征組合下的模型決策邊界和數據點分布。plt.subplots_adjust?函數調整了子圖之間的水平和垂直間距，讓圖形看起來更美觀、布局更合理。

5. 訓練模型并繪制決策邊界

接下來，是整個案例的核心部分。我們要對不同的特征組合，分別訓練決策樹模型和隨機森林模型，并繪制它們的決策邊界。

for pairidx, pair in enumerate([[0, 1], [0, 2], [0, 3], [1, 2]]):X = iris.data[:, pair]y = iris.target# 訓練決策樹模型clf_tree = DecisionTreeClassifier().fit(X, y)# 訓練隨機森林模型clf_rf = RandomForestClassifier(n_estimators=100, random_state=42).fit(X, y)# 繪制決策邊界ax = sub[pairidx // 2, pairidx % 2]DecisionBoundaryDisplay.from_estimator(clf_tree,X,cmap=plt.cm.RdYlBu,response_method="predict",ax=ax,xlabel=iris.feature_names[pair[0]],ylabel=iris.feature_names[pair[1]],)ax.set_title("Decision Tree")DecisionBoundaryDisplay.from_estimator(clf_rf,X,cmap=plt.cm.RdYlBu,response_method="predict",ax=ax,xlabel=iris.feature_names[pair[0]],ylabel=iris.feature_names[pair[1]],)ax.set_title("Random Forest")

在這個循環中，我們依次選取不同的特征組合（比如花瓣長度和花瓣寬度、萼片長度和花瓣長度等）。對于每一組特征，我們先提取對應的特征數據?X?和類別標簽?y，然后分別創建并訓練一個決策樹模型?clf_tree?和一個隨機森林模型?clf_rf。隨機森林模型中，我們設置了?n_estimators=100，表示由 100 棵決策樹組成森林，random_state=42?是為了保證每次運行代碼時，模型的隨機性是一致的，結果可復現。

訓練好模型后，我們使用?DecisionBoundaryDisplay.from_estimator?函數分別繪制決策樹和隨機森林模型的決策邊界。在繪制時，我們指定了顏色映射?cmap=plt.cm.RdYlBu，這樣不同區域會根據模型的預測結果顯示不同顏色，方便我們區分。同時，我們給每個子圖設置了標題，標明是決策樹還是隨機森林的決策邊界。

6. 繪制訓練數據點

在繪制完決策邊界后，我們還要把訓練數據點繪制到圖上，用不同顏色表示不同的類別，這樣可以更直觀地看到模型的分類效果。

for i, color in zip(range(n_classes), plot_colors):idx = np.where(y == i)ax.scatter(X[idx, 0],X[idx, 1],c=color,label=iris.target_names[i],cmap=plt.cm.RdYlBu,edgecolor="black",s=15,)

這段代碼遍歷每個類別，找到屬于該類別的數據點索引?idx，然后使用?ax.scatter?函數將這些數據點以散點的形式繪制在對應的子圖上，并且設置了顏色、標簽等屬性。

7. 添加標題和圖例

最后，我們給整個圖形添加一個總標題，并且添加圖例，方便我們理解圖中不同顏色和區域代表的含義。

plt.suptitle("Decision Surface of Decision Trees and Random Forest on Pairs of Features")
plt.legend(loc="lower right", borderpad=0, handletextpad=0)
plt.axis("tight")
plt.show()

plt.suptitle?函數添加了總標題，說明了圖中展示的是決策樹和隨機森林在不同特征組合下的決策表面。plt.legend?函數添加了圖例，指定了圖例的位置在右下角等屬性。plt.axis("tight")?調整了坐標軸的范圍，讓圖形展示更緊湊。最后?plt.show()?顯示出整個圖形。?

通過這個案例，我們可以清楚地看到決策樹和隨機森林的決策邊界，以及它們在 Iris 數據集不同特征組合下是如何進行分類的。這有助于我們深入理解這兩種模型的本質，以及它們處理數據和進行分類的方式。希望大家通過這個例子，能對決策樹和隨機森林模型有更深刻的認識！

---

K-Means 聚類

我們通過一個具體的例子來學習 K-Means 聚類算法。K-Means 聚類是一種無監督學習方法，主要用于將數據點劃分成不同的簇，幫助我們理解數據內在的結構。

首先，我們使用 Scikit - Learn 中的工具來生成一個合成數據集。我們調用?make_blobs?函數，設定生成 1000 個數據點，每個數據點有 2 個特征，并且將這些數據點自然地分成 4 個簇，同時設置隨機數種子為 42，這樣每次運行代碼得到的數據集都是一樣的，方便我們進行調試和對比。代碼如下：

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobsn_samples = 1000
n_features = 2
n_clusters = 4
random_state = 42
X, _ = make_blobs(n_samples=n_samples, n_features=n_features, centers=n_clusters, random_state=random_state)

生成數據集后，我們開始構建 K-Means 模型。我們創建一個?KMeans?對象，指定要將數據分成 4 個簇，同樣設置隨機數種子為 42，以保證模型初始化的隨機性一致。代碼是：

kmeans = KMeans(n_clusters=n_clusters, random_state=random_state)

接下來，我們用生成的數據?X?來訓練這個 K-Means 模型，讓模型學習數據的分布特征，找到合適的簇劃分方式。訓練代碼為：

kmeans.fit(X)

模型訓練完成后，我們可以獲取兩個重要的結果。一個是簇中心，也就是每個簇的中心點坐標，它代表了這個簇數據點的平均特征位置；另一個是每個數據點所屬的簇的標簽，通過這個標簽我們能知道每個數據點被劃分到了哪個簇。獲取這兩個結果的代碼如下：

cluster_centers = kmeans.cluster_centers_
labels = kmeans.labels_

最后，為了更直觀地看到 K-Means 聚類的效果，我們使用?matplotlib?庫來繪制圖形。我們把所有的數據點繪制出來，根據它們所屬的簇用不同顏色表示，這樣可以很清楚地看到不同簇的數據點分布情況。同時，我們用紅色的 “X” 標記出每個簇的中心位置。繪制圖形的代碼如下：

plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50, alpha=0.7)
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1], c='red', s=200, marker='X', label='Cluster Centers')
plt.title('K-Means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()

上圖展示了 K-Means 聚類是如何將數據點分成不同的簇的。通過這個例子，我們可以更好地理解 K-Means 聚類的本質，即通過尋找合適的簇中心，將數據點劃分到不同的簇中，從而揭示數據的結構特征。希望大家通過這個案例，能對 K-Means 聚類算法有更深入的認識！

---

集成方法實戰

集成方法的核心思路是把多個模型組合起來，發揮它們的優勢，從而獲得比單個模型更好的性能。我們會使用 Scikit-Learn 庫創建一個合成數據集，并運用RandomTreesEmbedding和ExtraTreesClassifier兩種方法，來展示集成方法的具體應用和效果。

1. 生成合成數據集

首先，我們用make_circles函數創建一個合成數據集。這個數據集由兩類數據點組成，形狀類似兩個同心圓，參數factor=0.5控制兩個圓的距離，noise=0.05給數據添加一些隨機噪聲，讓數據更接近真實情況，random_state=0保證每次運行代碼生成的數據都一樣。代碼如下：

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_circles
from sklearn.decomposition import TruncatedSVD
from sklearn.ensemble import ExtraTreesClassifier, RandomTreesEmbedding
from sklearn.naive_bayes import BernoulliNBX, y = make_circles(factor=0.5, random_state=0, noise=0.05)

這里X存儲的是數據點的特征，每個數據點有 2 個特征；y是數據點的類別標簽，用來表示每個數據點屬于哪一類。

2. 使用 RandomTreesEmbedding 轉換數據

接下來，我們用RandomTreesEmbedding對數據進行轉換。這個方法通過構建多棵決策樹，把原始數據映射到一個新的特征空間。我們設置使用 10 棵樹（n_estimators=10），樹的最大深度為 3（max_depth=3），并固定隨機種子（random_state=0），讓結果可重復。轉換后的數據X_transformed，特征數量會比原始數據多很多。

hasher = RandomTreesEmbedding(n_estimators=10, random_state=0, max_depth=3)
X_transformed = hasher.fit_transform(X)

3. 數據降維以便可視化

由于X_transformed特征太多，不方便直接可視化，我們用TruncatedSVD進行降維，把數據從高維降到 2 維，這樣就能在平面上畫圖展示了。

svd = TruncatedSVD(n_components=2)
X_reduced = svd.fit_transform(X_transformed)

4. 訓練樸素貝葉斯分類器

降維后，我們用BernoulliNB訓練一個樸素貝葉斯分類器。樸素貝葉斯基于概率來預測數據的類別，我們用轉換后的數據X_transformed和對應的標簽y來訓練它，讓它學習數據的分類規律。

nb = BernoulliNB()
nb.fit(X_transformed, y)

5. 訓練 ExtraTreesClassifier

同時，我們用ExtraTreesClassifier也訓練一個模型，用來和前面的方法做對比。這個模型和隨機森林類似，也是由多棵決策樹組成，但在構建樹的過程中有一些不同，能提高模型的性能。我們設置樹的最大深度為 3，使用 10 棵樹，同樣固定隨機種子。

trees = ExtraTreesClassifier(max_depth=3, n_estimators=10, random_state=0)
trees.fit(X, y)

6. 可視化展示

為了直觀地看到不同方法的效果，我們繪制了 4 個子圖：

1. 原始數據圖：展示最初生成的合成數據，能看到兩類數據點像兩個套在一起的圓圈分布。

ax = plt.subplot(221)
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, edgecolor="k")
ax.set_title("Original Data (2d)")
ax.set_xticks(())
ax.set_yticks(())

????????2.?降維后的數據圖：展示RandomTreesEmbedding轉換并經TruncatedSVD降維后的數據分布，能看到數據在新的 2 維空間中的樣子。

ax = plt.subplot(222)
ax.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y, s=50, edgecolor="k")
ax.set_title("Truncated SVD reduction (2d) of transformed data (%dd)" % X_transformed.shape[1]
)
ax.set_xticks(())
ax.set_yticks(())

?????????3. 轉換數據后的樸素貝葉斯分類結果圖：在原始數據空間中，用RandomTreesEmbedding轉換網格數據，再用樸素貝葉斯預測每個網格點屬于某一類的概率，通過顏色深淺展示預測結果，疊加原始數據點，能看到模型劃分的決策邊界。

h = 0.01
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))transformed_grid = hasher.transform(np.c_[xx.ravel(), yy.ravel()])
y_grid_pred = nb.predict_proba(transformed_grid)[:, 1]ax = plt.subplot(223)
ax.set_title("Naive Bayes on Transformed data")
ax.pcolormesh(xx, yy, y_grid_pred.reshape(xx.shape))
ax.scatter(X[:, 0], X[:, 1,], c=y, s=50, edgecolor="k")
ax.set_ylim(-1.4, 1.4)
ax.set_xlim(-1.4, 1.4)
ax.set_xticks(())
ax.set_yticks(())

????????4.?ExtraTreesClassifier 分類結果圖：同樣在原始數據空間，用ExtraTreesClassifier預測每個網格點屬于某一類的概率，展示決策邊界和原始數據點，對比兩種方法的分類效果。

y_grid_pred = trees.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]ax = plt.subplot(224)
ax.set_title("ExtraTrees predictions")
ax.pcolormesh(xx, yy, y_grid_pred.reshape(xx.shape))
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, edgecolor="k")
ax.set_ylim(-1.4, 1.4)
ax.set_xlim(-1.4, 1.4)
ax.set_xticks(())
ax.set_yticks(())

最后，我們調整子圖布局，讓整個圖表看起來更協調，并顯示圖表。

plt.tight_layout()
plt.show()

通過這個案例，我們知道了如何使用RandomTreesEmbedding和ExtraTreesClassifier這兩種集成方法處理數據，還通過可視化，直觀地看到了不同方法劃分的決策邊界和分類效果。這能幫助我們更好地理解集成方法的工作原理，以及組合多個模型是如何提升整體性能的。如果在學習過程中有任何疑問，歡迎一起討論！

---

高斯混合模型（GMM）實戰

大家好！今天我們來學習高斯混合模型（Gaussian Mixture Model，簡稱 GMM），這是一個在聚類和密度估計方面非常有用的概率模型。GMM 的基本思路是，假設我們的數據是由多個高斯分布（也就是常見的正態分布，像鐘形曲線那樣）混合而成的，每個高斯分布就代表一個聚類。接下來，我們用 Scikit - Learn 庫中的GaussianMixture類，結合經典的 Iris 數據集，手把手教大家如何構建和可視化 GMM 模型。

1. 準備數據

我們使用 Scikit - Learn 內置的 Iris 數據集，這個數據集很經典，包含了三種不同種類鳶尾花的特征測量數據。具體來說，每個鳶尾花樣本都有四個特征：花萼長度、花萼寬度、花瓣長度和花瓣寬度。我們通過下面的代碼加載數據集：

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.mixture import GaussianMixture
from sklearn.decomposition import PCA
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target

這里，X是一個二維數組，每一行代表一個鳶尾花樣本，每一列對應一個特征；y是樣本的真實類別標簽，不過在聚類任務里，我們一開始不會用到它，主要用X里的特征數據來做聚類。

2. 構建和訓練 GMM 模型

接下來，我們創建 GMM 模型。因為 Iris 數據集里有三種鳶尾花，所以我們設定聚類數量為 3，也就是讓模型把數據分成 3 個簇。

from sklearn.mixture import GaussianMixture
n_components = 3  # 聚類數量設為3
gmm = GaussianMixture(n_components=n_components)

創建好模型后，我們用數據X來訓練它，讓模型自己去估計每個高斯分布的參數，比如均值（可以理解為每個簇的中心位置）和協方差矩陣（描述特征之間的相關性和數據的分散程度）。

gmm.fit(X)

3. 進行預測和獲取概率

模型訓練好后，我們可以做兩件事：

• 預測聚類標簽：讓模型判斷每個樣本屬于哪個聚類，得到每個樣本的聚類標簽。

labels = gmm.predict(X)

• 獲取概率：除了知道樣本屬于哪個聚類，我們還能知道每個樣本屬于每個聚類的概率，這是 GMM 很獨特的地方。

probs = gmm.predict_proba(X)

4. 數據降維以便可視化

由于原始數據有四個特征，很難直接在平面上畫出來展示。所以我們用主成分分析（PCA）把數據降到 2 維，這樣就能在一張圖上直觀地看到聚類效果了。

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X)

5. 繪制可視化結果

我們繪制兩張圖來展示 GMM 的聚類效果：

• 左邊的圖：根據預測的聚類標簽，把數據點畫出來，不同標簽的數據點用不同顏色表示。這樣一眼就能看出模型把數據分成了哪幾個簇。

plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=labels, cmap='viridis')
plt.title('GMM Clustering')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')

• 右邊的圖：根據每個樣本屬于每個聚類的概率來畫圖，概率越高，顏色越深。通過這張圖，我們能看到每個數據點和不同聚類之間的 “親密程度”，也就是屬于某個聚類的可能性大小。

plt.subplot(1, 2, 2)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=probs, cmap='viridis', marker='x')
plt.title('GMM Clustering (Probabilities)')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.show()

通過這個案例，我們完整地演示了如何用 GMM 對 Iris 數據集進行聚類，從數據準備、模型構建，到最后的可視化展示。上圖看到了?GMM 把數據分成了哪些簇，可以看出每個樣本屬于不同簇的概率情況。GMM 是一個很強大的聚類算法，尤其適合數據呈現多種分布的情況。如果在學習過程中有任何疑問，歡迎一起交流討論！?

---

梯度提升樹實戰

梯度提升樹（Gradient Boosting）算法，這是一種非常強大的集成學習方法，通過不斷疊加多個決策樹，逐步提升模型的預測能力。我們會用 Scikit-Learn 庫中的GradientBoostingClassifier，通過實際案例演示如何用它解決分類問題，還會對比帶提前停止機制的版本，看看優化后的效果。

1. 準備數據

我們選用 Scikit-Learn 內置的三個不同數據集：

1. Iris 數據集：經典的花卉分類數據，包含三種鳶尾花的花萼、花瓣等特征，用來預測花的種類。
2. 隨機生成的分類數據集：用make_classification函數生成 800 個樣本數據，適合測試模型在常規分類任務中的表現。
3. Hastie 數據集：用make_hastie_10_2函數生成 2000 個樣本，數據分布更復雜，能考驗模型處理復雜問題的能力。

import time
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, ensemble
from sklearn.model_selection import train_test_split# 數據集和名稱
data_list = [datasets.load_iris(return_X_y=True),datasets.make_classification(n_samples=800, random_state=0),datasets.make_hastie_10_2(n_samples=2000, random_state=0),
]
names = ["Iris Data", "Classification Data", "Hastie Data"]

這里data_list存儲加載后的數據集，每個數據集包含特征數據X和對應的標簽y；names記錄數據集的名稱，方便后續展示。

2. 構建和訓練模型

我們要構建兩種梯度提升樹模型：

• 普通梯度提升樹：用GradientBoostingClassifier創建，設定使用 200 棵決策樹（n_estimators=200），讓模型逐步疊加這些樹來優化預測效果。
• 帶提前停止機制的梯度提升樹：同樣基于GradientBoostingClassifier，除了設置 200 棵樹，還添加了提前停止參數。validation_fraction=0.2表示從訓練數據中拿出 20% 作為驗證集，n_iter_no_change=5和tol=0.01組合起來表示，如果連續 5 次迭代中，驗證集上的損失降低幅度小于 0.01，就停止訓練，避免模型過擬合。

# 初始化列表用于存儲結果
n_gb = []
score_gb = []
time_gb = []
n_gbes = []
score_gbes = []
time_gbes = []n_estimators = 200for X, y in data_list:X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)# 創建梯度提升樹模型gbes = ensemble.GradientBoostingClassifier(n_estimators=n_estimators,validation_fraction=0.2,n_iter_no_change=5,tol=0.01,random_state=0,)gb = ensemble.GradientBoostingClassifier(n_estimators=n_estimators, random_state=0)# 訓練并記錄時間start = time.time()gb.fit(X_train, y_train)time_gb.append(time.time() - start)start = time.time()gbes.fit(X_train, y_train)time_gbes.append(time.time() - start)

在循環中，我們對每個數據集都做同樣的操作：先把數據拆成 80% 的訓練集和 20% 的測試集；然后分別訓練兩種模型，記錄每個模型的訓練時間。

3. 評估模型并記錄結果

訓練完成后，我們用測試集評估模型的表現：

• 計算準確率：用score方法計算模型在測試集上的分類準確率，數值越高說明模型預測得越準。
• 記錄迭代次數：對于帶提前停止機制的模型，查看實際訓練了多少棵樹就停止了，和普通模型固定的 200 棵樹做對比。

    # 計算準確度并記錄score_gb.append(gb.score(X_test, y_test))score_gbes.append(gbes.score(X_test, y_test))# 記錄訓練的迭代次數n_gb.append(gb.n_estimators_)n_gbes.append(gbes.n_estimators_)

4. 可視化對比結果

最后，我們用 Matplotlib 繪制柱狀圖，直觀對比兩種模型在不同數據集上的表現：

# 繪制圖形
bar_width = 0.2
n = len(data_list)
index = np.arange(0, n * bar_width, bar_width) * 2.5
index = index[0:n]plt.figure(figsize=(10, 6))
plt.bar(index, score_gb, bar_width, label='Gradient Boosting', color='b', alpha=0.7)
plt.bar(index + bar_width, score_gbes, bar_width, label='Gradient Boosting with Early Stopping', color='g', alpha=0.7)
plt.xlabel('Dataset')
plt.ylabel('Accuracy')
plt.title('Accuracy of Gradient Boosting vs. Early Stopping Gradient Boosting')
plt.xticks(index + bar_width, names)
plt.legend(loc='best')
plt.tight_layout()
plt.show()

圖中藍色柱子代表普通梯度提升樹模型的準確率，綠色柱子代表帶提前停止機制的模型準確率。橫軸是不同的數據集名稱，縱軸是準確率數值。通過這張圖，我們能清楚看到：在不同復雜度的數據上，兩種模型的表現有什么差異，提前停止機制是否真的能提升模型性能、減少訓練時間。

通過這個案例，我們完整展示了梯度提升樹解決分類問題的全流程，還對比了優化后的模型效果。梯度提升樹不僅能用于分類，解決回歸問題也很出色，在實際的數據分析和機器學習項目中應用非常廣泛。如果對代碼或原理有疑問，歡迎隨時交流！

?

---

AdaBoost 實戰

AdaBoost 算法在回歸任務中的應用。想象一下，我們手頭有一組數據，這些數據背后存在著某種復雜的非線性關系，而且還摻雜著一些隨機的噪聲干擾。我們的目標是利用 AdaBoost 回歸器，把這種隱藏的關系找出來，并通過可視化直觀地看到它的預測效果。

1. 生成模擬數據

為了演示 AdaBoost 在回歸任務中的表現，我們先創建一組模擬數據。這里用的是常見的正弦函數，再加上一些隨機噪聲，來模擬現實中復雜多變的數據情況。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import AdaBoostRegressor# 生成模擬數據
rng = np.random.default_rng(42)
X = np.sort(5 * rng.random(80))[:, np.newaxis]
y = np.sin(X).ravel() + rng.normal(0, 0.1, X.shape[0])

在這段代碼里，我們設定了隨機數種子為 42，這樣每次運行代碼生成的數據都是一樣的，方便對比和調試。X是通過生成 80 個 0 到 5 之間的隨機數，并整理成一列數據。y則是基于X計算正弦值，再加上一些服從正態分布的隨機噪聲，模擬出實際觀測到的目標值。

2. 構建和訓練模型

接下來，我們分別用普通的決策樹和 AdaBoost 回歸器構建模型，并進行訓練。

• 普通決策樹：我們創建一個決策樹回歸器，限制樹的最大深度為 4，避免模型過于復雜導致過擬合。

regr_1 = DecisionTreeRegressor(max_depth=4)

• AdaBoost 回歸器：AdaBoost 是一種集成學習算法，它的核心思路是把多個 “弱學習器” 組合起來，變成一個強大的模型。這里我們以決策樹作為弱學習器，設定總共使用 300 個決策樹，并且固定隨機種子，保證結果可復現。

regr_2 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=300, random_state=42)

?然后，我們用生成的X和y數據分別訓練這兩個模型：

regr_1.fit(X, y)
regr_2.fit(X, y)

訓練完成后，使用這兩個模型對數據進行預測：

y_1 = regr_1.predict(X)
y_2 = regr_2.predict(X)

3. 可視化對比結果

為了直觀地看出兩個模型的預測效果差異，我們使用matplotlib和seaborn庫繪制圖形。

# 可視化結果
colors = sns.color_palette("colorblind")
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color=colors[0], label="training samples")
plt.plot(X, y_1, color=colors[1], label="Decision Tree", linewidth=2)
plt.plot(X, y_2, color=colors[2], label="AdaBoost", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree and AdaBoost Regression")
plt.legend()
plt.show()

在繪制的圖形中：

• 散點表示我們生成的原始數據點，能看到數據分布呈現出一定的非線性趨勢，但又因為噪聲的存在顯得有些雜亂。
• 藍色的線是普通決策樹的預測結果，它雖然也嘗試去擬合數據，但可能因為數據的復雜性和噪聲影響，有些地方和真實數據偏差較大。
• 橙色的線是 AdaBoost 回歸器的預測結果，明顯可以看出它更好地貼合了數據的整體變化趨勢，即使面對噪聲點，也能保持相對穩定的預測效果。

通過這個案例，我們完整地展示了 AdaBoost 在回歸任務中的應用過程。從生成模擬數據、構建模型，到最后的可視化對比，我們清楚地看到了 AdaBoost 是如何通過組合多個弱學習器，提升模型對復雜非線性數據的擬合能力和對噪聲的抵抗能力。

---

用神經網絡分類 2D 數據集：

要用神經網絡處理幾個經典的二維數據集分類問題。我們會使用三個合成數據集：形狀像彎彎月亮的 “月亮形數據集”，由一大一小兩個圓圈構成的 “圓形數據集”，還有加入了一些噪聲但基本能直線分開的 “線性可分離數據集”。通過調整神經網絡里的正則化參數，看看對模型性能有什么影響，最后再把決策邊界畫出來，直觀感受模型是怎么分類的。

1. 數據準備

我們先準備好要用的數據集：

• 月亮形數據集：用make_moons函數生成，數據點分布成兩個相互交疊的半圓形，就像兩個彎彎的月亮碰在一起，noise=0.3表示給數據加上一些隨機噪聲，讓分類更有挑戰性。
• 圓形數據集：用make_circles函數生成，包含一大一小兩個同心圓的數據點，noise=0.2是噪聲，factor=0.5控制兩個圓的距離。
• 線性可分離數據集：用make_classification函數創建，設定只有 2 個有效特征，沒有冗余特征，每個類別數據聚成一團，再加入少量噪聲，讓數據不是完美分開。

# 創建數據集
datasets = [make_moons(noise=0.3, random_state=0),make_circles(noise=0.2, factor=0.5, random_state=1),make_classification(n_features=2, n_redundant=0, n_informative=2, random_state=0, n_clusters_per_class=1)
]

2. 構建神經網絡模型

我們搭建一個有兩層隱藏層的多層感知機（MLP）分類器。這里重點調整正則化參數alpha，alpha越大，對模型復雜度的限制就越強，能防止模型過擬合。我們選了 5 個不同的alpha值，從 0.1 到 10，覆蓋不同的正則化強度。

# 定義不同的alpha值
alphas = np.logspace(-1, 1, 5)# 為每個alpha值構建一個MLP分類器
classifiers = []
names = []
for alpha in alphas:classifiers.append(MLPClassifier(solver="lbfgs",alpha=alpha,random_state=1,max_iter=2000,hidden_layer_sizes=[10, 10]))names.append(f"alpha {alpha:.2f}")

每個模型都用 “lbfgs” 優化器，設定隨機種子保證結果可重復，最多訓練 2000 次，兩層隱藏層都包含 10 個神經元。

3. 數據預處理與模型訓練

拿到數據后，先做標準化處理，把數據縮放到統一范圍，這樣模型訓練更快更穩定。再把數據分成 60% 的訓練集和 40% 的測試集。

for X, y in datasets:X = StandardScaler().fit_transform(X)X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)

4. 可視化決策邊界和模型性能

我們創建一個大畫布，準備把不同數據集、不同alpha值下的模型表現都畫出來。先畫出原始數據點，訓練集用亮色，測試集顏色淡一點，方便區分。

figure = plt.figure(figsize=(17, 9))
i = 1
for X, y in datasets:# 數據預處理和劃分X = StandardScaler().fit_transform(X)X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)# 確定繪圖范圍并生成網格x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))cm = plt.cm.RdBucm_bright = ListedColormap(["#FF0000", "#0000FF"])ax = plt.subplot(len(datasets), len(classifiers) + 1, i)ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6)ax.set_xlim(xx.min(), xx.max())ax.set_ylim(yy.min(), yy.max())ax.set_xticks(())ax.set_yticks(())i += 1

接著，對每個alpha值對應的模型，先在訓練集上訓練，再用測試集計算準確率。根據模型輸出類型，繪制決策邊界，顏色深的地方表示模型對分類更確定，顏色淺的地方表示分類不那么明確。最后在圖上標注模型的準確率，方便對比。

    for name, clf in zip(names, classifiers):ax = plt.subplot(len(datasets), len(classifiers) + 1, i)clf.fit(X_train, y_train)score = clf.score(X_test, y_test)if hasattr(clf, "decision_function"):Z = clf.decision_function(np.column_stack([xx.ravel(), yy.ravel()]))else:Z = clf.predict_proba(np.column_stack([xx.ravel(), yy.ravel()]))[:, 1]Z = Z.reshape(xx.shape)ax.contourf(xx, yy, Z, cmap=cm, alpha=0.8)ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright, s=25)ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, s=25, alpha=0.6)ax.set_xlim(xx.min(), xx.max())ax.set_ylim(yy.min(), yy.max())ax.set_xticks(())ax.set_yticks(())ax.set_title(name)ax.text(xx.max() - 0.3, yy.min() + 0.3, f"{score:.3f}", size=15, horizontalalignment="right")i += 1

最后調整一下子圖布局，讓圖表看起來更整齊，再展示出來。

plt.tight_layout()
plt.show()

通過這張圖表，我們能清楚看到：不同正則化參數下，神經網絡在各個數據集上的決策邊界怎么變化，準確率有什么不同。正則化參數太小，模型可能過度擬合訓練數據；參數太大，又可能欠擬合，抓不住數據規律。

最后

今天我們學習了 scikit-learn 在監督學習里用神經網絡分類的方法，后續還會分享更多 scikit-learn 在其他場景的應用，記得關注哦！