目錄

問題 1：足式機器人運動規劃 & 控制的典型流程 (pipline)

1.1 問題

1.2 目標

1.3 典型流程（Pipeline）

1.3.1?環境感知（Perception）

1.3.2?高層規劃（High-Level Planning）

1.3.3?足跡規劃（Footstep Planning）

1.3.4?身體軌跡生成（Body Trajectory Generation / Trajectory Optimization）

補充論文

1.3.5?全身控制（Whole-Body Control, WBC）

1.3.6?反饋閉環

問題 2：接觸事件建模 & 混合系統控制

2.1 問題

2.2 背景

2.3 接觸建模方法

2.4 混合系統控制方法

問題 3：處理模型誤差

3.1 問題

3.2 背景

3.3 處理方法

問題 4：自動駕駛汽車的安全交互 & 駕駛模式差異

4.1 問題

4.2 意外交互中的安全 & 合規

4.3 普通駕駛 vs. 賽車 的區別

• 港科廣?馬老師?的機器人學 課堂討論 (seminar)?記錄
• 問題驅動的學習，有助于進一步提出有價值的問題
• 梳理機器人運動規劃和控制領域的主流問題和技術
• 以問題為框架，梳理論文更高效

問題 1：足式機器人運動規劃 & 控制的典型流程 (pipline)

1.1 問題

足式機器人 因其在復雜地形中的高機動性而備受關注。那么，足式機器人的 運動規劃與控制 的 典型流程（pipeline）是怎樣的？

1.2 目標

• 使足式機器人在復雜環境中穩定、高效地移動

1.3 典型流程（Pipeline）

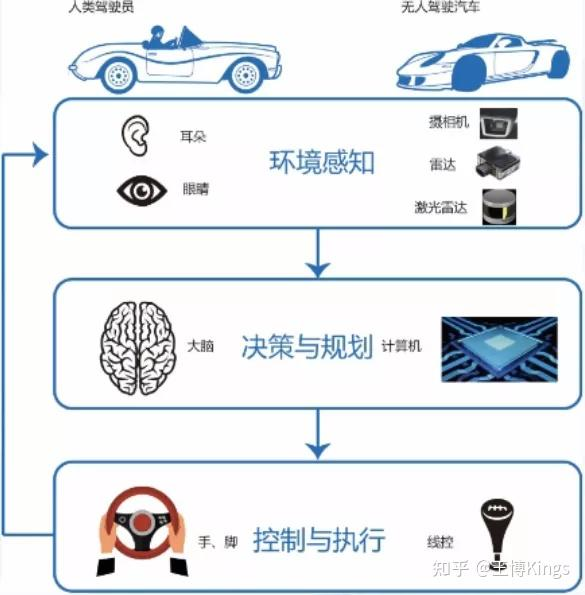
1.3.1?環境感知（Perception）

• 使用傳感器（激光雷達 LiDAR、攝像頭 Camera、慣性測量單元 IMU、關節編碼器、足底力傳感器等）獲取環境信息（地形、障礙物）和機器人自身狀態（位置、姿態、速度、接觸狀態）
• 生成環境地圖（如點云圖、柵格圖、高程圖）和估計機器人狀態（State Estimation）。狀態估計通常融合 IMU、運動學和接觸信息

1.3.2?高層規劃（High-Level Planning）

• 根據任務目標（如“到達 A 點”）和環境地圖，規劃出一條全局路徑（通常是機器人身體中心 質心 (CoM) [質量中心]?的路徑），避開大的障礙物。常用算法如圖搜索（A*, RRT*）

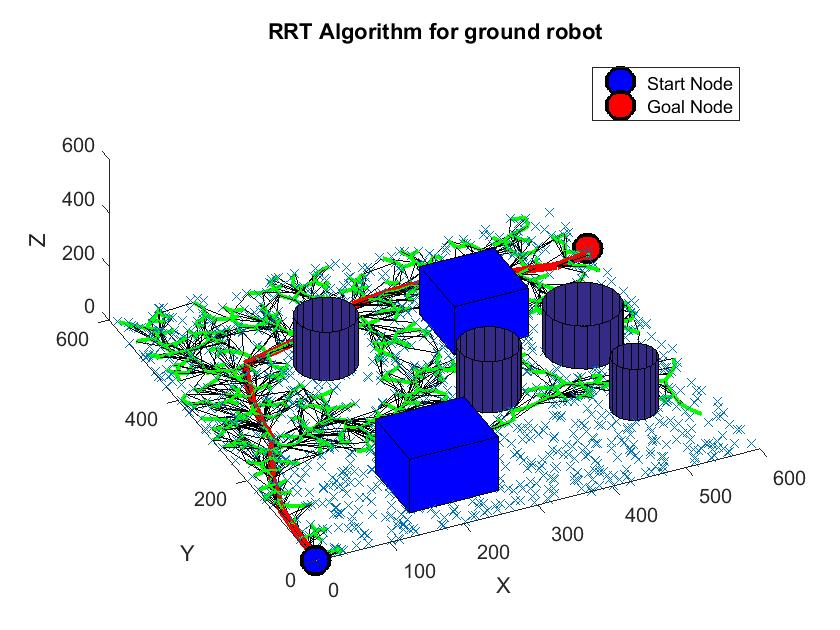
• 最新的接入LLM的高層規劃導航方法有：

1.3.3?足跡規劃（Footstep Planning）

• 根據高層規劃的路徑和局部地形信息，規劃出一系列離散的足底落點位置和時間。
• 需要考慮：運動學可達性（腿長限制）、運動穩定性（如基于 ZMP - Zero Moment Point、Capture Point 的判據）、地形適應性（尋找平坦、穩固的落腳點）、避免碰撞等

1.3.4?身體軌跡生成（Body Trajectory Generation / Trajectory Optimization）

• 根據規劃好的足跡，生成機器人身體（CoM）和擺動腿（Swing Leg）的連續運動軌跡
• 通常是一個優化問題，目標是平滑、節能、穩定，同時滿足動力學約束（如 ZMP 約束）、運動學約束和足跡約束

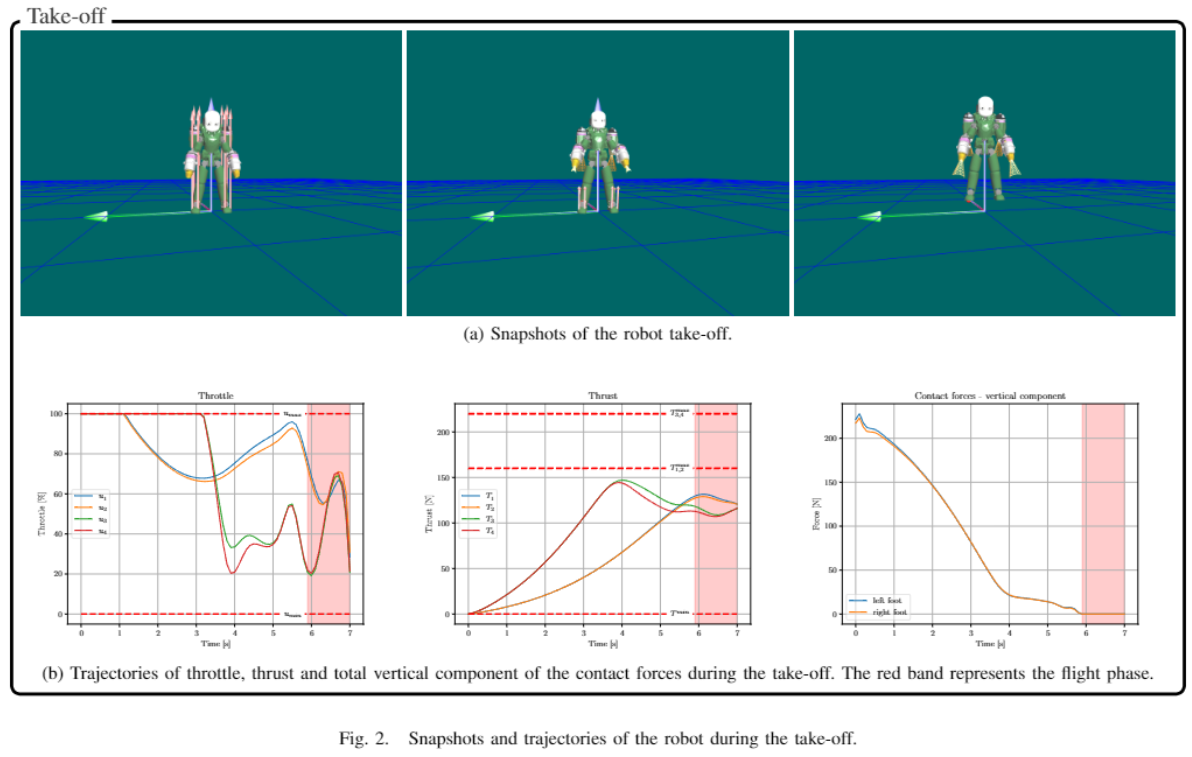
補充論文

• 其它的軌跡生成的工作（不是全身軌跡，只是手臂軌跡生成）

• 最新的接入LLM的端到端視覺-語言-動作模型有：（直接從感知 -> 動作軌跡生成）

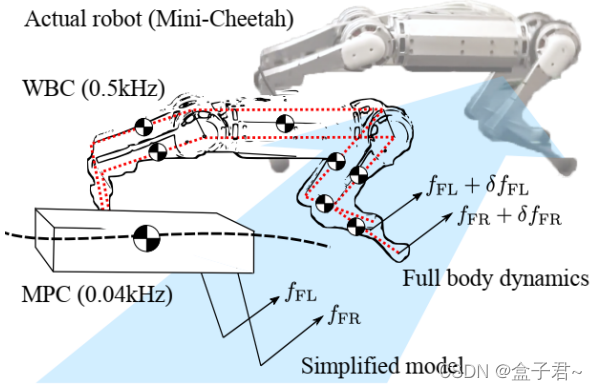
1.3.5?全身控制（Whole-Body Control, WBC）

• 這是最底層的控制。根據期望的身體軌跡、足部軌跡和接觸狀態，計算需要施加到每個關節的力矩（Torque）
• 通常也表述為一個優化問題（如二次規劃 QP），目標是精確跟蹤期望運動，同時滿足多個任務和約束：
  • 任務（優先級可能不同）： 保持身體姿態、跟蹤 CoM 軌跡、跟蹤擺動腿軌跡、維持接觸力等。
  • 約束： 關節角度/速度/力矩限制、摩擦力約束（Friction Cone）、接觸運動學約束（著地腳速度為零）
• 常用方法包括基于任務空間/操作空間（Task/Operational Space）的控制、基于逆動力學的控制等。

1.3.6?反饋閉環

• 整個流程是閉環的。感知到的實際狀態會反饋給規劃和控制層，用于糾正偏差
• 例如，如果實際落腳點與計劃不符，或身體姿態發生傾斜，控制器會實時調整

問題 2：接觸事件建模 & 混合系統控制

2.1 問題

接觸事件 會導致系統狀態發生不連續的跳變（例如速度突變）。我們如何有效地在 系統動力學 中為這種接觸進行 建模？對于這類具有 非光滑動力學 特性的 混合系統（hybrid systems），我們又該如何進行 控制？

2.2 背景

• 接觸（如機器人腳落地、物體碰撞）是許多物理系統中常見的現象。它會導致速度、加速度等狀態量瞬間改變，使得系統的動力學模型在接觸點變得不連續、非光滑。這類系統既包含連續變化的動態（如空中飛行），又包含離散的事件（接觸瞬間），因此被稱為“混合系統”

2.3 接觸建模方法

• 剛體碰撞模型（Impact Maps）： 這是最經典的方法之一。假設碰撞時間無限短，利用沖量-動量定理來計算碰撞后的速度。通常會引入“恢復系數”（Coefficient of Restitution, e）來描述碰撞的能量損失程度（e=1 為完全彈性碰撞， e=0 為完全非彈性碰撞）。對于多點接觸或復雜幾何體，需要考慮接觸點的位置、法線方向以及摩擦（如庫侖摩擦模型）
• 連續接觸力模型（Penalty Methods / Regularization）： 這種方法避免了不連續性。它將接觸力模擬為非常“硬”的彈簧和阻尼器。當物體相互穿透時，會產生一個非常大的排斥力將它們推開。優點是模型是連續的，易于仿真和控制設計；缺點是需要選擇合適的剛度和阻尼系數，可能導致數值計算上的“剛性問題”（stiffness），并且物理真實性可能不如碰撞模型
• 互補約束（Complementarity Constraints）： 這是目前在機器人學和仿真中非常流行且物理意義明確的方法。它將接觸條件（如：不穿透距離 d≥0、接觸力 fn?≥0、兩者不能同時大于零 d?fn?=0）以及摩擦力（如最大靜摩擦力約束）表示為一組數學上的互補約束（通常是線性互補問題 LCP 或非線性互補問題 NCP）。這種方法能夠精確地描述“接觸/分離”的邏輯切換
• 事件驅動方法（Event-Driven）： 精確地檢測接觸事件發生的時間點，然后在事件點切換動力學模型或應用沖擊模型。這在仿真中很常用，但在實時控制中可能較難實現

2.4 混合系統控制方法

• 分段控制/切換系統理論（Switched Systems）： 為系統的每種模態（接觸/非接觸）分別設計控制器，并設計切換邏輯來保證穩定性。挑戰在于處理切換瞬間的狀態跳變和保證切換過程的穩定性
• 模型預測控制（MPC）： MPC 天然適合處理約束。可以將互補約束或接觸力約束直接納入優化問題中，預測未來一段時間的系統行為并計算最優控制輸入。對于混合系統，需要使用混合整數規劃（Mixed-Integer Programming）或專門處理互補約束的優化算法
• 能量/耗散理論（Passivity-Based Control）： 利用系統的能量特性來設計控制器，特別是在處理接觸時的能量交換和耗散
• 力/阻抗控制（Force/Impedance Control）： 不直接控制位置，而是控制機器人與環境交互時的力或表現出的機械阻抗（力與位移/速度的關系）。這對于處理接觸時的不確定性和保證柔順性非常有效。
• 基于學習的控制： 利用強化學習等方法讓系統自主學習如何在接觸中穩定運動

問題 3：處理模型誤差

3.1 問題

模型 總歸是 近似 的。我們如何處理模型中存在的 誤差？

3.2 背景

• 任何數學模型都是對現實世界的簡化和近似。誤差來源包括：參數不確定（質量、摩擦系數未知）、未建模的動態（如柔性、驅動器延遲）、傳感器噪聲、環境干擾等

3.3 處理方法

• 魯棒控制（Robust Control）： 設計控制器時就考慮模型不確定性的存在范圍，目標是即使在最壞的模型誤差情況下，系統依然能保持穩定并滿足一定的性能指標。常用方法包括 H-infinity 控制、滑模控制（Sliding Mode Control）等。滑模控制對匹配不確定性（matching uncertainty）尤其魯棒
• 自適應控制（Adaptive Control）： 控制器能夠在線估計模型參數或不確定性的大小，并根據估計結果調整自身的控制律，以適應模型變化
• 迭代學習控制（Iterative Learning Control, ILC）： 適用于重復性任務。通過每次試驗的誤差來修正下一次試驗的控制輸入，逐步提高性能，對模型精度要求不高
• 基于觀測器的控制： 設計狀態觀測器（如卡爾曼濾波器、擴展卡爾曼濾波器、無跡卡爾曼濾波器、粒子濾波器等）來估計系統內部狀態和干擾，并將估計值用于反饋控制，以補償模型誤差和噪聲的影響
• 數據驅動/學習方法：
  • 系統辨識（System Identification）： 在控制設計前，通過實驗數據更精確地估計模型參數或建立數據驅動模型
  • 殘差建模（Residual Modeling）： 用機器學習模型（如高斯過程、神經網絡）來學習“標稱模型”（nominal model）與實際系統之間的差異（殘差），并將這個學習到的殘差加入到控制設計中
  • 強化學習（Reinforcement Learning）： 直接從與環境的交互中學習最優控制策略，可以不依賴精確的模型
• 增加反饋增益： 在一定范圍內，提高反饋控制器的增益可以增強系統抑制干擾和克服模型誤差的能力，但過高的增益可能導致系統不穩定或放大噪聲

問題 4：自動駕駛汽車的安全交互 & 駕駛模式差異

4.1 問題

自動駕駛汽車 有時需要進行 激進駕駛（aggressive driving）并與其它車輛進行復雜的 交互。在這種 意外交互 發生時，我們如何保證車輛行為的 安全 和 合規（compliant）？此外，普通駕駛 和 賽車（car racing）之間有什么 區別？

4.2 意外交互中的安全 & 合規

• 環境感知與預測： 精確感知周圍車輛、行人、障礙物的位置、速度和意圖。利用運動模型、交互模型甚至機器學習模型預測它們未來的行為軌跡
• 風險評估： 實時評估潛在的碰撞風險（如 Time-to-Collision, TTC）和其他危險情況
• 決策規劃：
  • 規則遵從： 嚴格遵守交通規則（如保持車道、安全距離、讓行規則）。形式化方法（如 RSS - Responsibility-Sensitive Safety）可以提供可驗證的安全保證
  • 防御性駕駛策略： 預留足夠的安全裕度，對其他道路使用者的不確定行為保持警惕，選擇風險最低的策略
  • 應急處理（Contingency Planning）： 預先設計好應對突發危險情況（如前方急剎、鬼探頭）的緊急避險策略（緊急制動、緊急變道），并能在極短時間內觸發執行
• 運動控制： 精確、平穩地執行規劃出的軌跡，同時具備快速響應能力以執行緊急操作
• 冗余與容錯： 在傳感器、計算單元、執行器等關鍵部件上采用冗余設計，確保單一故障不會導致災難性后果
• V2X 通信（Vehicle-to-Everything）： 與其他車輛、基礎設施通信，提前獲取危險警告或意圖信息，有助于協同決策，但不能完全依賴

4.3 普通駕駛 vs. 賽車 的區別

• 目標（Objective）：
  • 普通駕駛：安全、舒適、高效（節能、省時）、遵守交通規則是首要目標
  • 賽車：唯一目標是最小化單圈時間。在規則允許范圍內，將車輛性能發揮到極限
• 運行環境（Environment）：
  • 普通駕駛：開放道路，環境復雜多變，充滿不確定性（其他車輛、行人、信號燈、天氣等）。需要遵守統一的交通法規
  • 賽車：封閉賽道，環境相對可控，對手是專業的賽車手（行為更激進但也相對可預測），有特定的比賽規則
• 車輛極限（Vehicle Limits）：
  • 普通駕駛：通常在車輛的遠低于極限的范圍內運行，追求平穩和舒適
  • 賽車：持續在車輛的物理極限（輪胎抓地力、發動機功率、剎車性能）邊緣駕駛
• 駕駛策略（Strategy）：
  • 普通駕駛：保持車道、平穩加減速、保持安全距離
  • 賽車：尋找最優“賽車線”（Racing Line），最大化利用賽道寬度，進行極限剎車、最大加速度出彎，容忍甚至利用輪胎的小幅滑移（Slip Angle）
• 風險容忍度（Risk Tolerance）：
  • 普通駕駛：極低，以避免任何事故為目標
  • 賽車：較高，為了追求速度，可以接受一定的失控風險（如打滑、沖出賽道）
• 控制算法側重：
  • 普通駕駛：側重安全性（碰撞避免）、平順性、規則遵守、能耗優化
  • 賽車：側重極限性能下的軌跡跟蹤、狀態估計（如輪胎滑移率）、最優控制（如最小時間 MPC）