決策樹

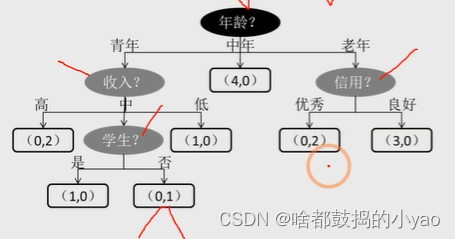
圖中的決策樹呈現自頂向下的生長過程，深色的橢圓表示樹的根節點；淺色的橢圓表示樹的中間節點；方框則表示樹的葉節點。

對于所有的非葉節點來說，都是用來表示條件判斷，而葉節點則存儲最終的分類結果，例如中年分支下的葉節點(4,0)表示4位客戶購買，0位客戶不購買。

決策樹節點字段的選擇

信息熵

我們首先了解下信息熵

熵原本是物理學中的一個定義，后來香農將其引申到了信息論領域，用來表示信息量的大小。信息量越大(分類越不“純凈”)，對應的熵值就越大，反之亦然。也就是信息量大，熵大，一個事件發生的概率小，反之亦然。信息熵的計算公式如下:

在實際應用中，會將概率p的值用經驗概率替換，所以經驗信息可以表示為：

舉個例子：以產品是否被購買為例，假設數據集一共包含14個樣本，其中購買的用戶有9個，沒有購買的用戶有5個，所以對于是否購買這個事件來說，它的經驗信息為：

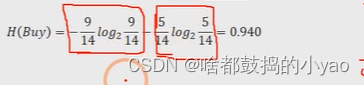
條件熵

判斷在某個條件下的信息熵為條件熵


比如：

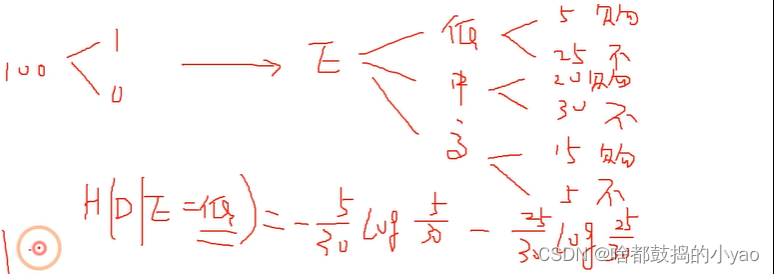
信息增益

對于已知的事件A來說，事件D的信息增益就是D的信息熵與A事件下D的條件熵之差，事件A對事件D的影響越大，條件熵H(D|A)就會越小(在事件A的影響下，事件D被劃分得越“純凈”)，體現在信息增益上就是差值越大，進而說明事件D的信息熵下降得越多。
所以，在根節點或中間節點的變量選擇過程中，就是挑選出各自變量下因變量的信息增益最大的。

其中：D是事件Y的所有可能

信息增益率

決策樹中的ID3算法使用信息增益指標實現根節點或中間節點的字段選擇，但是該指標存在一個非常明顯的缺點，即信息增益會偏向于取值較多的字段。
為了克服信息增益指標的缺點，提出了信息增益率的概念，"它的思想很簡單，就是在信息增益的基礎上進行相應的懲罰。信息增益率的公式可以表示為：

其中，HA為事件A的信息熵。事件A的取值越多，GainA(D)可能越大，但同時HA也會越大，這樣以商的形式就實現了GainA(D)的懲罰。

基尼指數

決策樹中的C4.5算法使用信息增益率指標實現根節點或中間節點的字段選擇，但該算法與ID3算法致，都只能針對離散型因變量進行分類，對于連續型的因變量就顯得束手無策了。
為了能夠讓決策樹預測連續型的因變量，Breiman等人在1984年提出了CART算法，該算法也稱為分類回歸樹，它所使用的字段選擇指標是基尼指數。

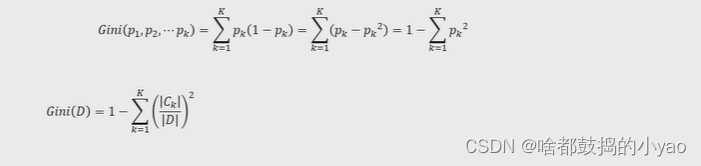
條件基尼指數

基尼指數增益

與信息增益類似，還需要考慮自變量對因變量的影響程度，即因變量的基尼指數下降速度的快慢，下降得越快，自變量對因變量的影響就越強。下降速度的快慢可用下方式子衡量：

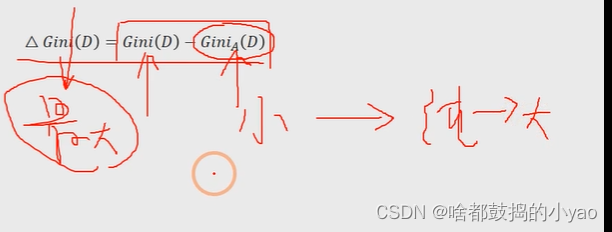
決策樹函數

DecisionTreeClassifier(criterion=‘gini’, splitter=‘best’,max_depth=None,min_samples split=2,min_samples_leaf=1,max_leaf_nodes=None,class_weight=None)
criterion: 用于指定選擇節點字段的評價指標，對于分類決策樹，默認為’gini’，表示采用基尼指數選擇節點的最佳分割字段；對于回歸決策樹，默認為’mse’，表示使用均方誤差選擇節點的最佳分割字段
splitter: 用于指定節點中的分割點選擇方法，默認為’best’，表示從所有的分割點中選擇最佳分割點如果指定為’random’，則表示隨機選擇分割點
max_depth: 用于指定決策樹的最大深度，默認為None，表示樹的生長過程中對深度不做任何限制
min_samples split: 用于指定根節點或中間節點能夠繼續分割的最小樣本量， 默認為2
min_samples leaf: 用于指定葉節點的最小樣本量，默認為1
max_leaf nodes:用于指定最大的葉節點個數，默認為None，表示對葉節點個數不做任何限制
class_weight:用于指定因變量中類別之間的權重，默認為None，表示每個類別的權重都相等;如果，則表示類別權重與原始樣本中類別的比例成反比;還可以通過字典傳遞類別之間的權重為balanced差異，其形式為{class label:weight}

隨機森林

利用Bootstrap抽樣法，從原始數據集中生成k個數據集，并且每個數據集都含有N個觀測和P個自變量。
針對每一個數據集，構造一棵CART決策樹，在構建子樹的過程中，并沒有將所有自變量用作節點字段的選擇，而是隨機選擇p個字段。
讓每一棵決策樹盡可能地充分生長，使得樹中的每個節點盡可能“純凈”，即隨機森林中的每一棵子樹都不需要剪枝。
針對k棵CART樹的隨機森林，對分類問題利用投票法，將最高得票的類別用于最終的判斷結果;對回歸問題利用均值法，將其用作預測樣本的最終結果。

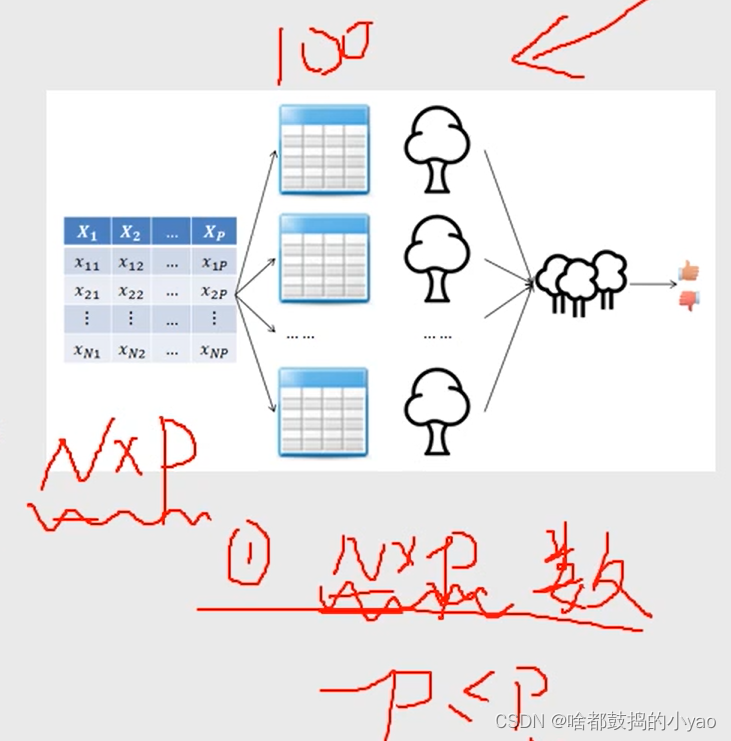
生成100個樹，每個數據集為一個樹

函數

RandomForestClassifier(n_estimators=10,criterion=‘gini’, max_depth=None,min_samples_split=2, min_samples_leaf=1,max_leaf_nodes=None, bootstrap=True, class_weight=None)
n_estimators: 用于指定隨機森林所包含的決策樹個數
criterion: 用于指定每棵決策樹節點的分割字段所使用的度量標準，用于分類的隨機森林，默認的criterion值為’gini’;用于回歸的隨機森林，默認的criterion值為’mse’
max_depth: 用于指定每棵決策樹的最大深度，默認不限制樹的生長深度
min _samples_split: 用于指定每棵決策樹根節點或中間節點能夠繼續分割的最小樣本量， 默認為2