學習資源：
全同態加密I：理論與基礎（上海交通大學 郁昱老師）
全同態加密II：全同態加密的理論與構造（Xiang Xie老師）

---

現在第二代（如BGV和BFV）和第三代全同態加密方案都是基于LWE構造的，現在先進的全同態方案也都是基于LWE的，所以本文總結一下LWE的基礎知識。
首先考慮，我們希望加密一個數$s$， 現在用一系列的$a_i$對$s$進行加密，得到$a_{i}s$，實際上通過求解最大公約數GCD就能求解出$s$。但是，如果加上一個隨機噪聲$e_i$，得到$a_{i}s+e_i$，那么將難以求解出$s$的值。這個過程就是我對LWE的簡單理解，所謂error就是一個noise。

全同態加密的計算過程分為三步：密鑰生成KeyGen、加密Enc、同態計算Eval、解密Dec。、

KeyGen：

首先構造出如上的等式，$s?A+e=sA+e$，然后得到公鑰pk（$?A$和$sA+e$的拼接），以及私鑰sk（$s$和1的拼接）。于是得到pk和sk滿足相乘后的結果是隨機噪聲e（接近0）。

Enc：

加密用的公鑰pk，r是一個只包含0或1的隨機向量，m是待加密的信息（放在向量的最低位上）。

Dec：

解密用的私鑰sk，和ct計算完內積后求mod 2得到解密結果。

正確性證明：

sk和pk相乘得到2e（KeyGen時滿足的條件），然后和r做內積得到一個很小的偶數噪聲，最終的結果就是m+很小的偶數噪聲，于是通過mod 2就能將噪聲消除，得到解密結果m。這也就是為什么構造的噪聲是2e，而不是e，我的理解就是希望通過構造偶數的隨機噪聲，從而在解密時方便用mod 2的方式消除掉噪聲。

安全性證明：

當pk是偽隨機的，r具有足夠高的熵（也就是隨機性很強？）時，pk和pk乘r都是偽隨機的。自然和帶m的向量相加后，加密結果也是偽隨機的。

下面是Xiang Xie老師的公式化描述：
加密公式：密文c = 公鑰pk ?? 隨機r + 明文m
解密公式：明文m = <密文sk, 私鑰sk> mod q mod 2

在這個基礎上，再mod 2就能解密出明文m的值。只要噪聲夠小，就能保證正確性。
這里有個需要區分的事情：以上$PK=(A,b=A{s}^{\prime }+2e)$是BGV方案，BFV則是$PK=(A,b=A{s}^{\prime }+e)$，區別是BGV將信息編碼在低位，而BFV將消息編碼在高位（學習BFV的時候會說明）。

Eval（加法同態和乘法同態）：

注意到同態加法或乘法都會帶來顯著的噪聲累積，并且乘法是呈平方增長趨勢。
然后說說如何解密同態乘的結果，下面的式子可以看到：兩個密文做乘法，等價于密文和私鑰分別先做tensor product，然后再做內積。因此，顯然密文和私鑰的大小都翻了一倍。Example是一個等價性的證明。

那么問題來了，如何將同態乘之后的密文大小和私鑰大小都恢復回去呢？這就是Key Switching解決的問題。

下面是Xiang Xie老師的描述：

Key Switching

目標是將密文和私鑰的大小恢復到線性大小。

現在求密文c1和c2的乘法：

以上過程基于比特分解這個概念：

下面是Xiang Xie老師的描述：

Key Switching的目標：將私鑰$\tilde{s}$下的$\tilde{c}$ 轉換為 私鑰$s$下的$c$，并且$\tilde{c}$和$c$都是加密的同一個明文。
這里有一個核心概念是Key Switching Key (KSK)，也就是用私鑰$s$來加密$\tilde{s}$。

通過Key Switching過程，可以推導出私鑰從$s?s$變成了線性的$s$，同時密文從$\tilde{c}$變成了線性的$c$。并且通過最后一行式子可以看出，Key Switching后的$?c,s?$和原來的$?\tilde{c},s?s?$之間相差了一個噪聲$2{\tilde{c}}^T\tilde{e}$，這部分是可以非常大的！所以到這里仍然沒辦法實現Key Switching。

這里引入了一個Gadget矩陣G：

于是，Key Switching的過程變成了下面這樣：

此時，增加的誤差就非常小了。
總結一下就是，通過Key Switching，原來私鑰$\tilde{s}=s?s$下的$\tilde{c}=c?c$，被轉換成了私鑰$s$下的$c$，注意Key Switching后的$s,c$都不是原來的值了（double check）。

對于BGV，加法的噪聲線性增長，乘法的噪聲平方增長，Key Switching雖然可以支持乘法了（限制sk變得特別大），但是實際上噪聲是在原本乘法噪聲基礎上加了一個很小的噪聲，總體也非常大。因此需要進一步降低這個噪聲。

Modulus Reduction

到這里，通過LWE實現了很小深度的同態乘法和加法計算，key switching則是對每層用新的密鑰，但是隨著計算深度加深，噪聲的擴大是爆炸性的，因此還不是一個levelled FHE（能計算指定深度的FHE）。
現在我們希望不借助bootstrapping，實現一個能計算一定深度的FHE，需要用到模數變換。

暫時沒太看懂中間的流程，簡而言之就是將密文c從模q的域變換到模p的域上（p<<q），于是噪聲等比例縮小，也就是大約縮小到原來的p/q倍。
下面是一個具體的例子：
如果不做Modulus Reduction，隨著深度加深，噪聲呈雙指數趨勢增長，level >= 3之后就會帶來解密錯誤。

如果每個level上做Modulus Reduction，那么噪聲也會被維持在一個絕對值范圍內，代價就是模數會不斷減小。

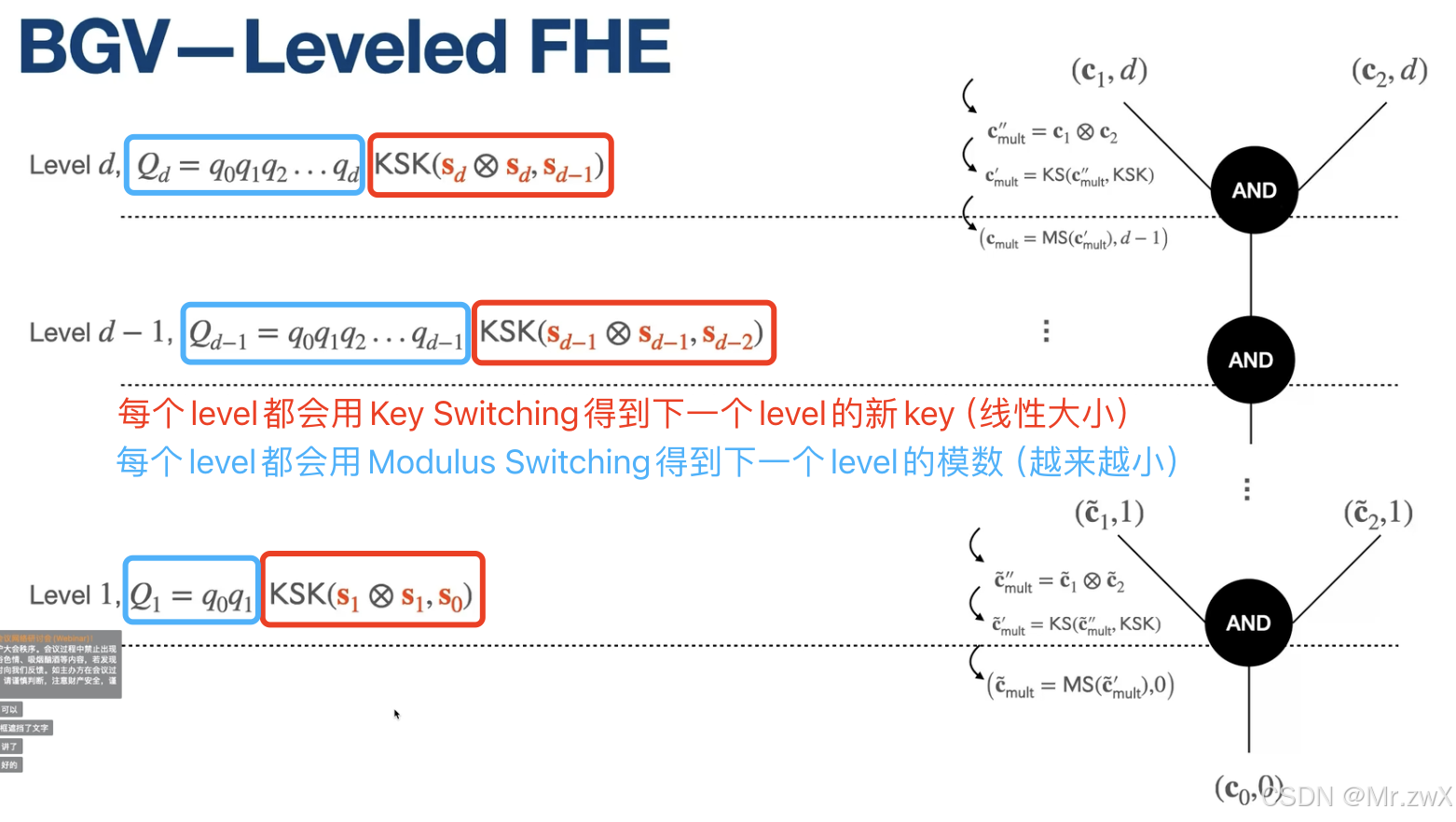
所以要想實現一個levelled FHE，可以設置一個模數$B^d$，然后就可以計算一個深度為$d$的電路了（其中$B$是刷新后密文的噪聲上界）。計算完$d$的深度后，模數應該是降低到$B$，要保證此時解密不出錯。BGV就是一種levelled FHE。