點贊👍👍收藏🌟🌟關注💖💖
你的支持是對我最大的鼓勵，我們一起努力吧!😃😃

1.排序數組

題目鏈接：912. 排序數組

題目描述：

算法原理：

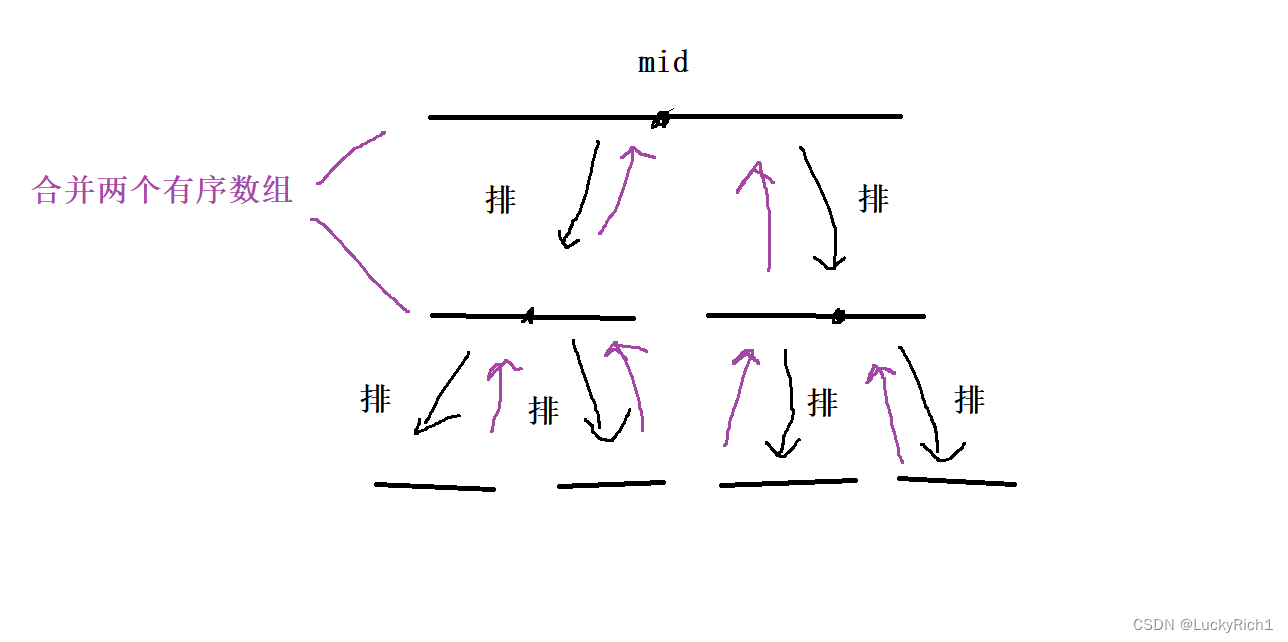
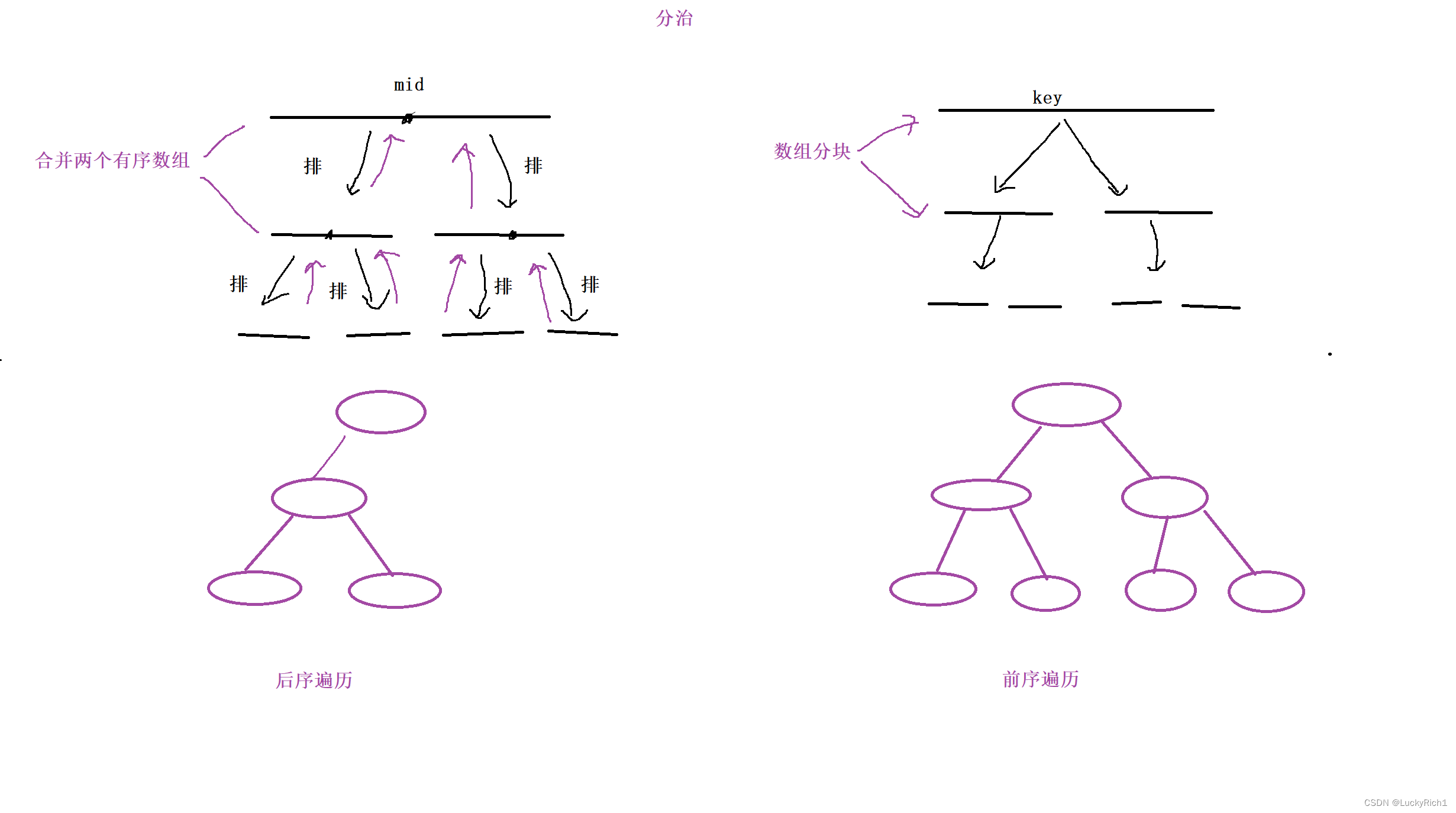
歸并排序的核心思想就是，選一個中間節點，將數組分成左右兩區間，先將左邊排排序相當于又是一個歸并過程，選一個中間節點然后在把左邊排序，當區間只有一個元素就可以向上返回。左邊拍完序，在對右邊排排序，當左右排好序后在合并，選擇小的插入，然后拷貝回原數組。

快速排序就是選擇一個key將數組分塊，然后左右繼續指向數組分塊的核心操作，當數組被分成一個元素或者沒有元素就結束分塊。

所以說快排和歸并非常類似，無非就是處理數組時間不一樣。歸并畫成樹就是一個后序，先處理左在處理右然后將左右合并，快排就是一個前序，先把數組分兩塊，然去搞左邊，左邊還是找一個key然后分成左和右。。。

class Solution {
public:vector<int> tmp;vector<int> sortArray(vector<int>& nums) {int n = nums.size();tmp.resize(n);Mergesort(nums, 0, n-1);return nums;}void Mergesort(vector<int>& nums, int left, int right){if(left >= right) return;// 1. 選擇中間點劃分區間int mid = left + (right - left) / 2;//[left ,mid] [mid+1, right]// 2.把左右區間排序Mergesort(nums, left, mid);Mergesort(nums, mid + 1, right);// 3.合并兩個有序數組int cur1= left, cur2 = mid + 1, i = 0;while(cur1 <= mid && cur2<= right)tmp[i++] = nums[cur1] < nums[cur2] ? nums[cur1++] : nums[cur2++];while(cu1 <= mid) tmp[i++] = nums[cur1++];while(cur2<= right) tmp[i++] = nums[cur2++];// 4.拷貝回原數組for(int i = left; i <= right; ++i)nums[i] = tmp[i - left];}
};

2.交易逆序對的總數

題目鏈接：LCR 170. 交易逆序對的總數

題目分析：

逆序對是兩個數前面的數比后面的大就是逆序對。

算法原理：

解法一：暴力解法->暴力枚舉
把所有二元組枚舉出來看看是不是逆序對。兩層for循環，但是超時。

如果想求整個數組的逆序對的時候，我把數組按照中間點分成兩部分，然后求整個數組逆序對的時候，先求出左邊逆序對的個數假設是a，在求出右邊逆序對的個數假設是b，然后左邊挑一個數右邊挑一個數求出一左一右的逆序對個數假設是c。那a+b+c 就是整個逆序對個數。因為本質還是暴力枚舉。

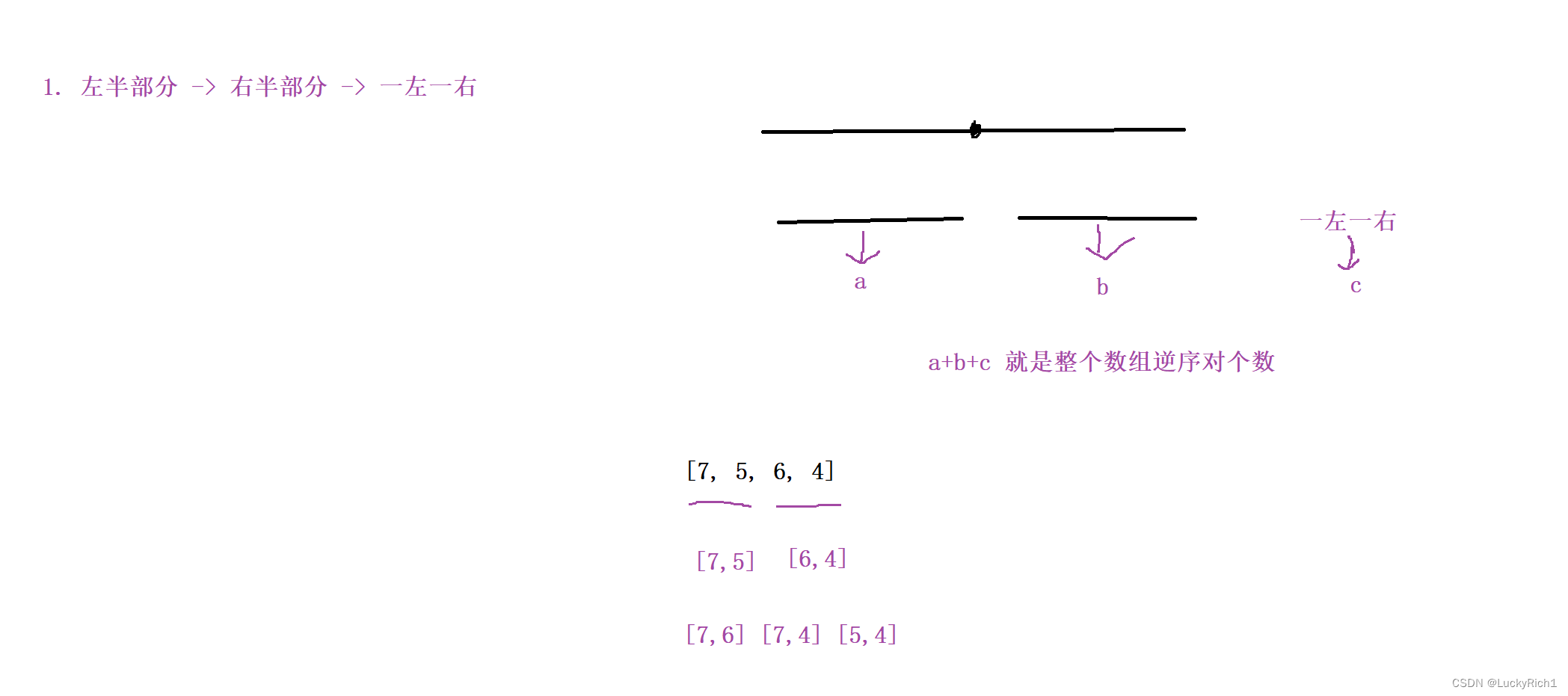
接下來我們在擴展一下，左半部分挑完之后排個序，右半部分跳完之后也排個序，然后左右都有序了在一左一右挑。這也是正確的，因為左半部分挑出來a后在排序不會影響結果， 右半部分挑出來b后在排序也不會影響結果。無非影響的是一左一右。但是我們左邊挑一個右邊挑一個是不管順序的。我們從左邊挑選一個數，然后在從右邊挑選比我小的數的個數就行了，從右邊挑選一個數，然后在從左邊挑選比我大的數的個數就行了，至于有沒有序和我沒關系。

當到這里的時候你會發現其實就是一個歸并排序。

解法二：利用歸并排序解決問題

選擇中間點把數組分成兩份，先去左區間找，如果左區間太大還可以在選個中間點在把數組分開直到不能分了就找逆序對，同理右邊也是。最后一左一右去找逆序對，這個策略正好對應歸并的過程。左半部分和右邊部分可以在遞歸中完成，我們的核心就是解決一左一右。同樣左邊部分+左排序放在一起遞歸中完整，右半部分+右排序放在一起遞歸完成，我們核心還是處理一左一右。因為遞歸都是的統一，所以一左一右后面在加一個排序。

左半部分 + 左排序 + 右半部分 + 右排序 + 一左一右 + 排序

這個時候有個小問題為什么非要排序呢？
雖然會有空間的開銷，但是會變得非常快。

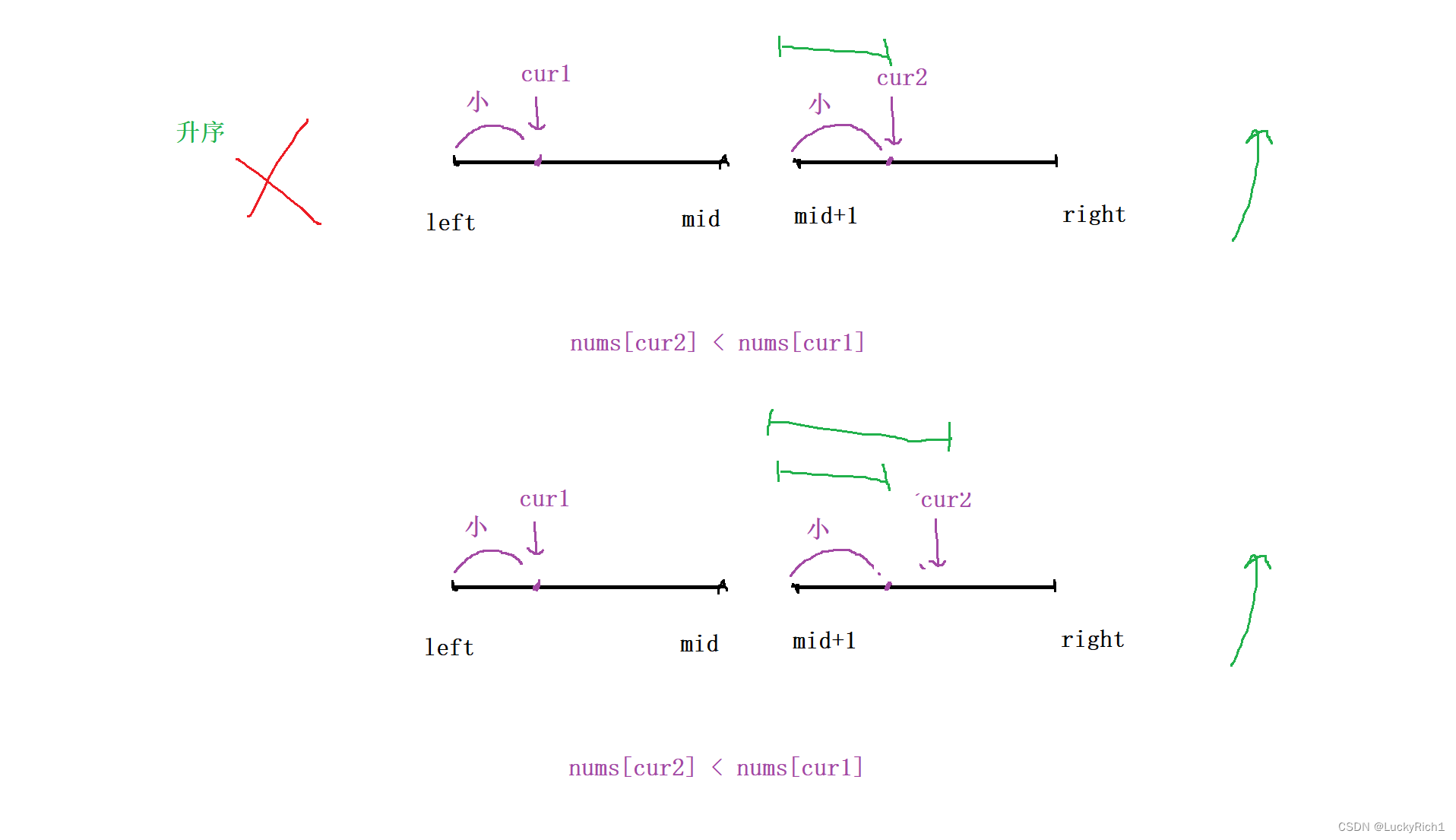
利用歸并排序后，數組左右區間已經是有序的了。假設是升序的。cur1和cur2之前的都是都是比cur1和cur2小的元素。

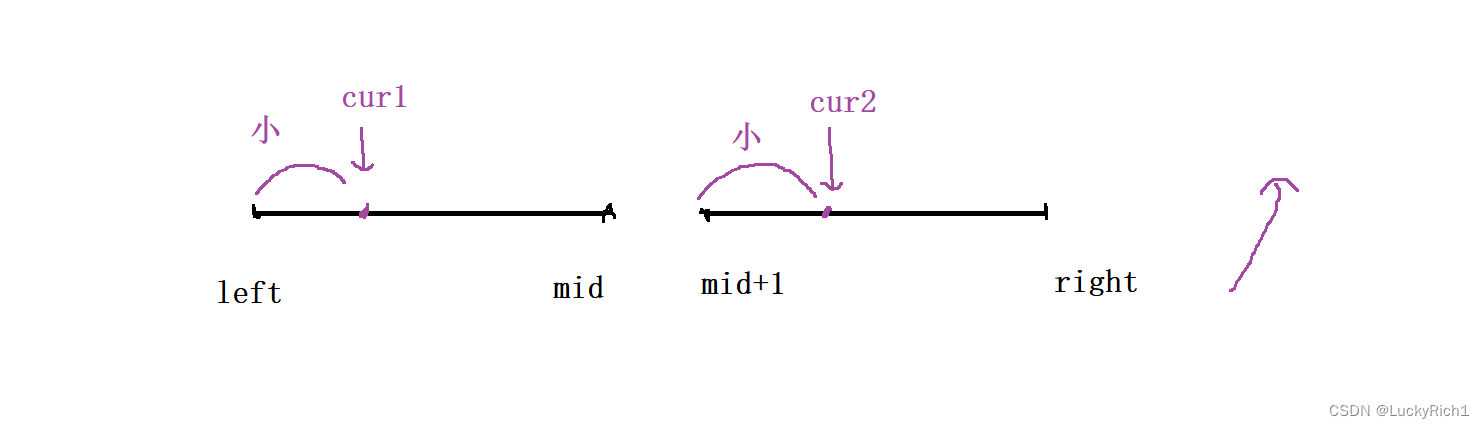
此時統計逆序對的話，按照如下策略可以一次找到一堆逆序對。

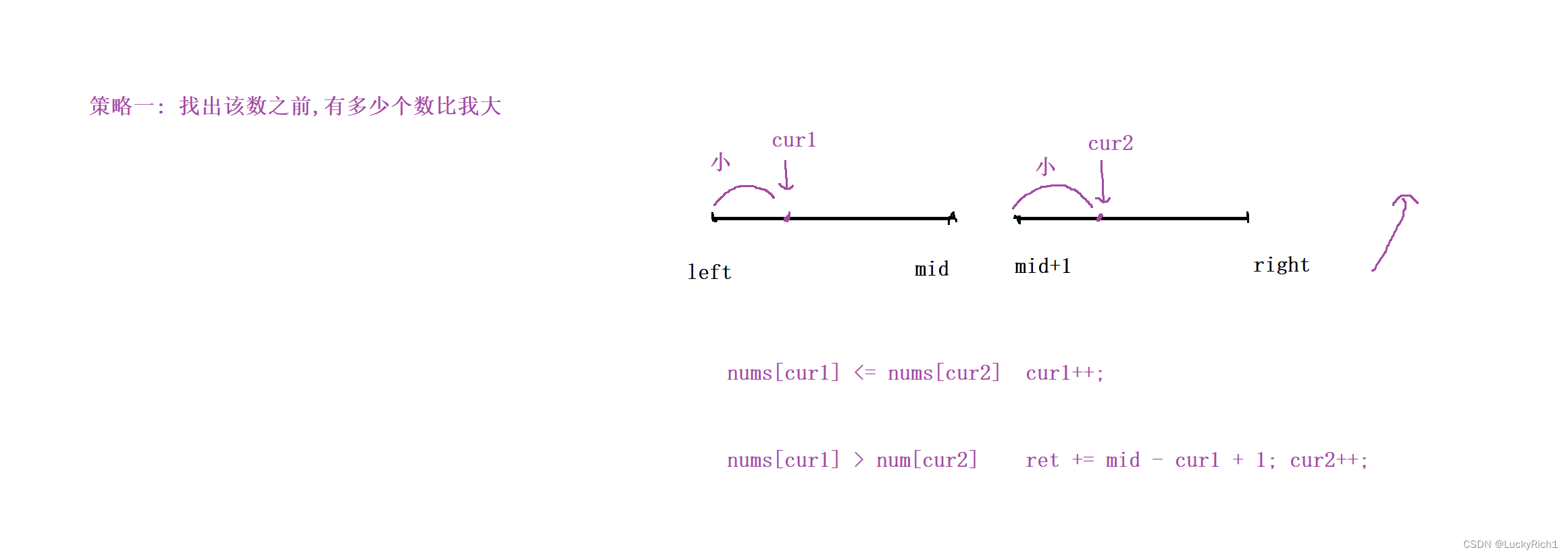
策略一：找出該數之前，多少個數比我大
此時我們固定的是cur2，因為我們是一左一右找，想要找比我大的數，盯的是后面的數，去看看左半部分有多少個比我大。此時就和歸并排序完美契合。無非就是三種情況。

當 nums[cur1] < nums[cur2]，說明還沒有在左邊找到比cur2大，所以cur1++

當 nums[cur1] == nums[cur2]，還是沒有在左邊找到比cur2大，所以cur1++

上面兩種情況可以合在一起
nums[cur1] <= nums[cur2]， cur1++，注意別忘記放進歸并數組里。

當 nums[cur1] > num[cur2] ，當前cur1比cur2元素大，別忘記我們可是升序數組，而且cur1比cur2的時候是cur1第一次出現比cur2大，cur1后面的元素都是比cur2大的！此時我們就是根據歸并排序的一次比較就找到一堆cur1比cur2大的數。此時用一個變量記錄一下cur1位置到左邊結束的位置的個數就可以了。ret += mid - cur1 + 1，一次就統計出來一大堆。而且cur1比cur2大的時候，我們下一次想讓cur2向后移，這正好和歸并排序一樣，讓小的往后移。

時間復雜度O(nlogn)

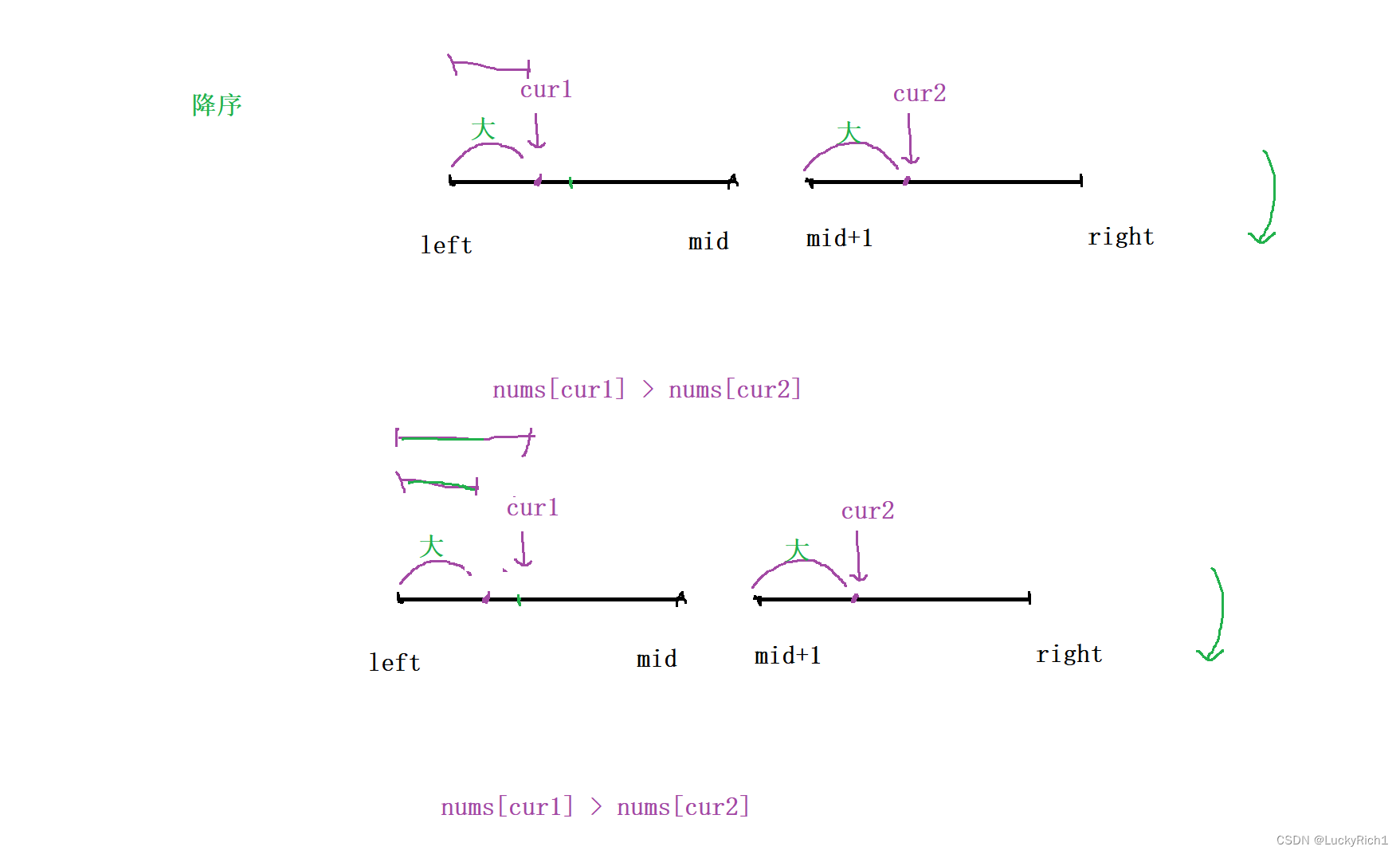
當前策略 找出該數之前，多少個數比我大，對于數組升序是沒問題的，那這個數組是降序的能不能解決這個問題，只要找比我大的不管升序還是降序都是固定cur2，在左邊找比cur2大的。

此時如果nums[cur1] > nums[cur2] ，要統計左邊開始到cur1有多個元素，但是有一個致命問題，cur1往前走一步的位置可能繼續比cur2大，還是要統計左邊開始到cur1有多個元素。然后你就會發現重復了。

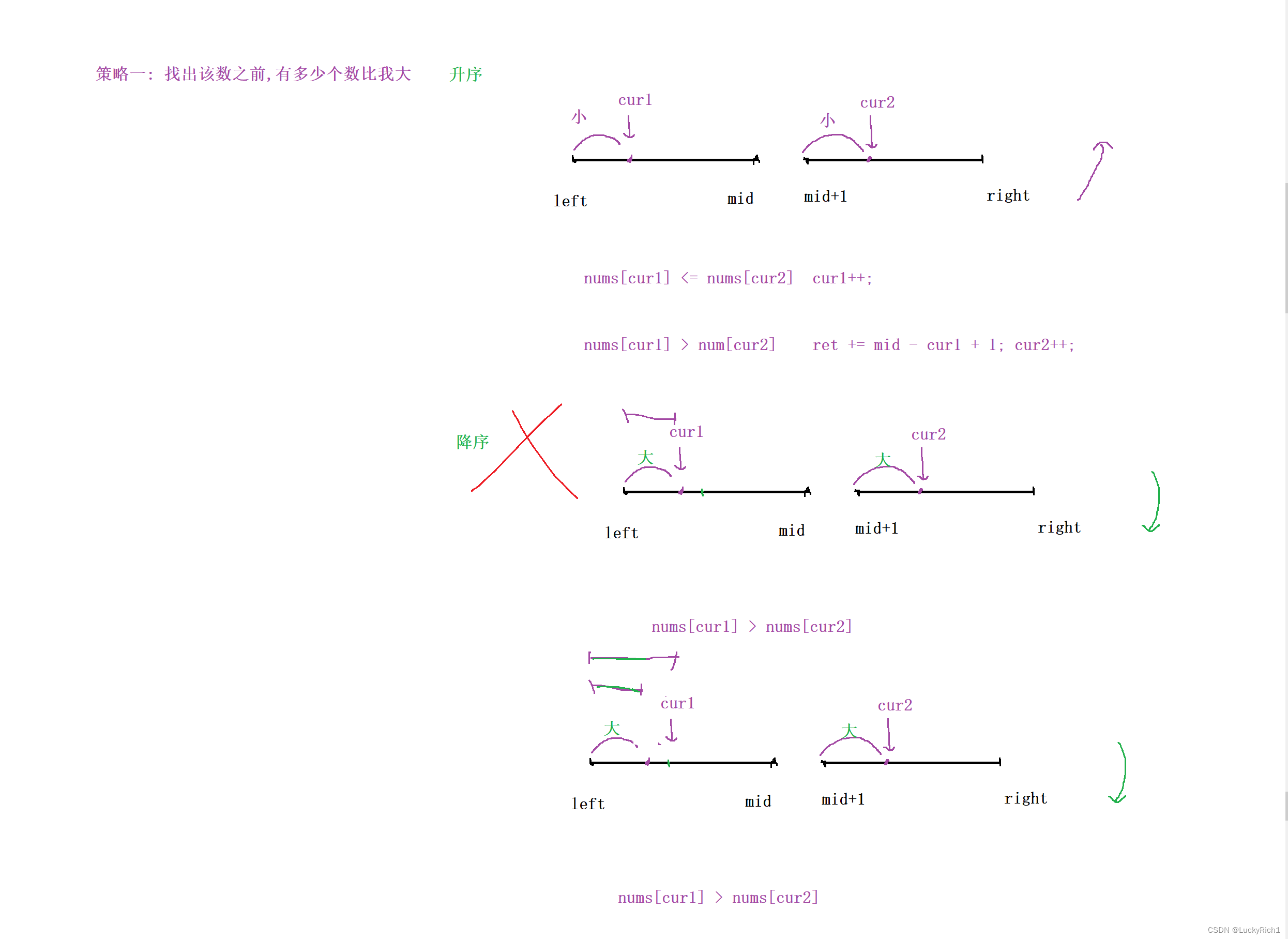
因此 策略一 ：找出該數之前，多少個數比我大 只能是升序，不能是降序！
固定cur2

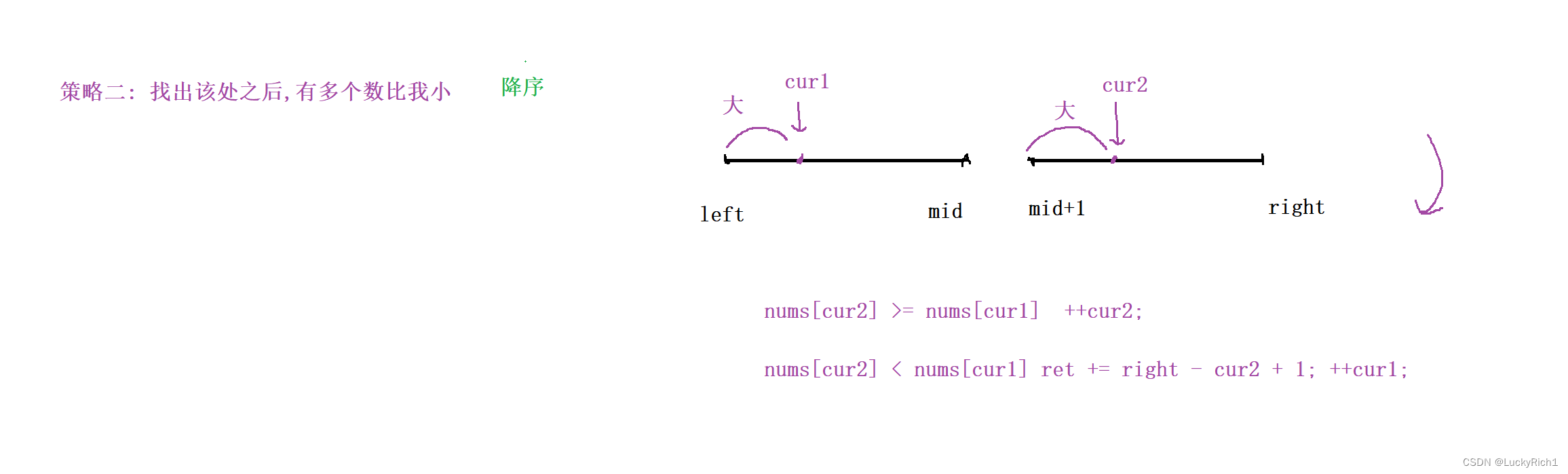
那降序就沒有用武之地了嘛？并不是。

策略二 ：找出該數之后，有多少個數比我小 只能是降序

固定cur1，在右邊部分找比cur1小的。當cur1比cur2大的時候，cur2是第一個出現的因為又是降序所以cur1比cur2后面元素都大，此時直接統計個cur2到右區間的個數 ret += right - cur2 + 1。而且統計完個數之后，已經把比cur1小的都找到了，此時讓cur1右移，而且正好和歸并排序是一樣的。

如果是升序的話也會有重復計算的問題。

至此算法原理就結束了，其實就是利用前兩部分析出來這道題可以用分治的方法來做。想求整個數組的逆序數，我可以先求左區間逆序數，在求右區間逆序數，然后一左一右挑一個求逆序數。所以這就是一個分支。然后發現數組有序的話可以通過一次比較統計一大推，因此可以用歸并排序來解決這個問題。

class Solution {vector<int> tmp;
public:int reversePairs(vector<int>& record) {int n = record.size();tmp.resize(n);return Mergesort(record, 0, n - 1);}int Mergesort(vector<int>& nums, int left, int right){if(left >= right) return 0;int ret = 0;// 1.找中間節點,將數組分成兩部分int mid = (left + right) >> 1;//[left,mid] [mid+1,right]// 2. 左邊的個數 + 排序  +  右邊的個數 + 排序ret += Mergesort(nums, left, mid);ret += Mergesort(nums, mid + 1, right);// 3. 一左一右的個數int cur1 = left, cur2 = mid + 1, i = 0;// while(cur1 <= mid && cur2 <= right) //升序// {//     if(nums[cur1] <= nums[cur2])//     {//         tmp[i++] = nums[cur1++];//     }//     else//     {//         ret += mid - cur1 + 1;//         tmp[i++] = nums[cur2++];//     }// }while(cur1 <= mid && cur2 <= right) //降序{if(nums[cur1] <= nums[cur2]){tmp[i++] = nums[cur2++];}else{ret += right - cur2 + 1;tmp[i++] = nums[cur1++];}}// 4. 處理一下排序while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];for(int j = left; j <= right; ++j)nums[j] = tmp[j - left];return ret;}
};

3.計算右側小于當前元素的個數

題目鏈接：315. 計算右側小于當前元素的個數

題目分析：

給一個nums數組，返回一個count數組，count[i] 的值是 對應nums[i] 右側小于 nums[i] 的元素的數量。

這也是求逆序對，但并不是求總體的逆序對個數，而是每個數的逆序對個數。

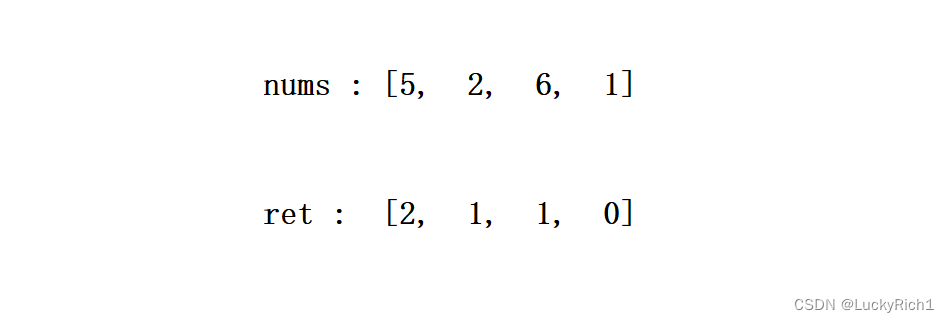
就是給一個數看看右邊比我少的有多少個。我們也是可以按照歸并排序來處理這個問題，但難得就是這返回數組怎么搞。

算法原理：

解法：歸并排序
選擇一個中間點，將數組分成左右兩部分，先在左半部分找，在到右半部分找，然后一左一右找。

左半部分 + 排序 + 右半部分 + 排序 + 一左一右 + 排序

策略二： 找出該數之后，有多少個數比我小 只能是降序
固定cur1

當 nums[cur1] <= nums[cur2] ，因為是降序此時并沒有找到有多少個元素比cur1小，所以不更新結果讓cur2++

當 nums[cur1] > nums[cur2] ，第一次出現cur1比cur2，因為是降序所以此時cur2后面所有元素都比cur1小，此時可以統計一大堆，但是我們這里可不是搞一個ret來記錄，而是搞一個數組，要把nums[cur1] 對應的 index(下標) 里面的 ret += right - cur2 +1

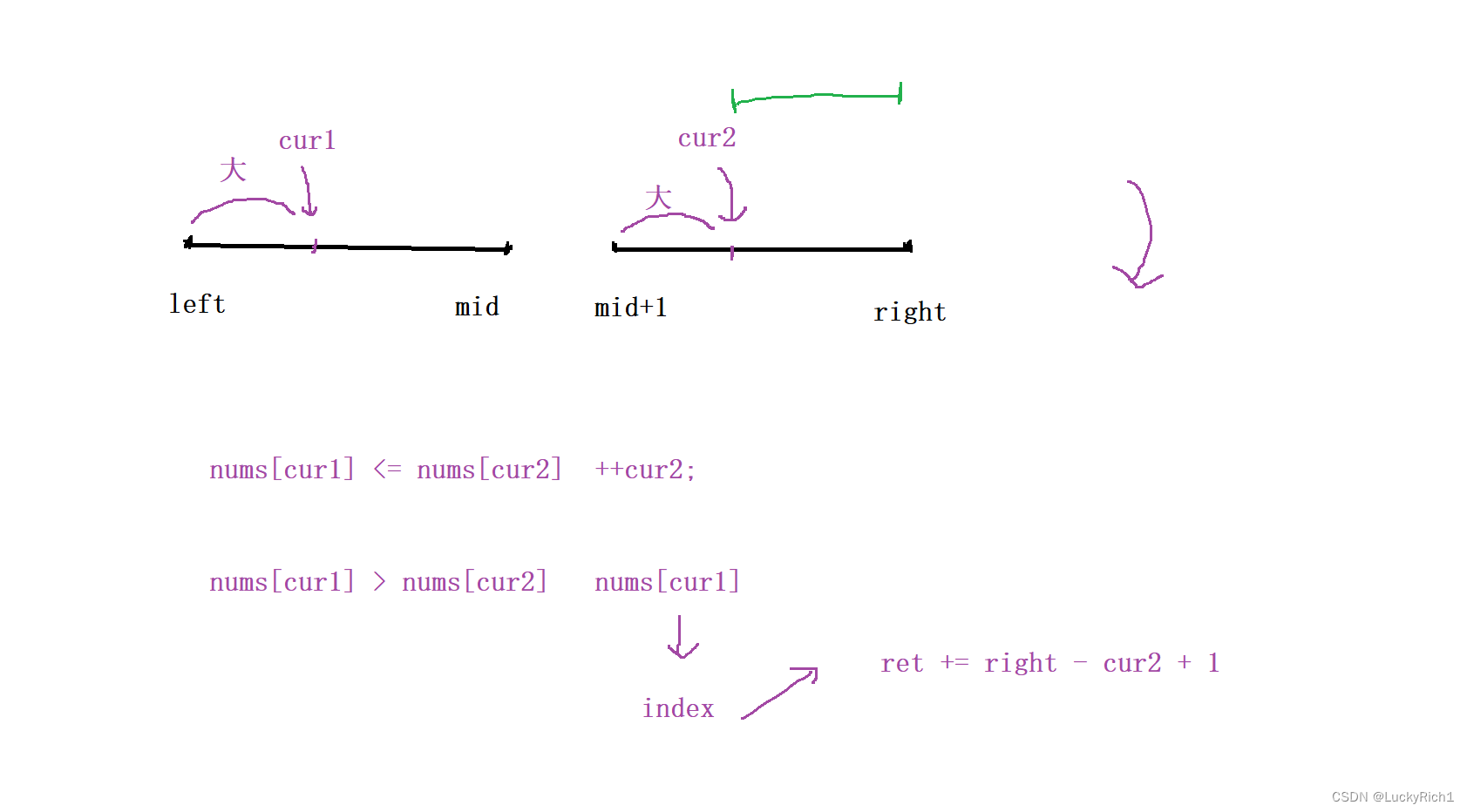
就比如這個數組，當計算出比當前位置元素小的個數是要把結果記錄到這個元素對應的位置上的。

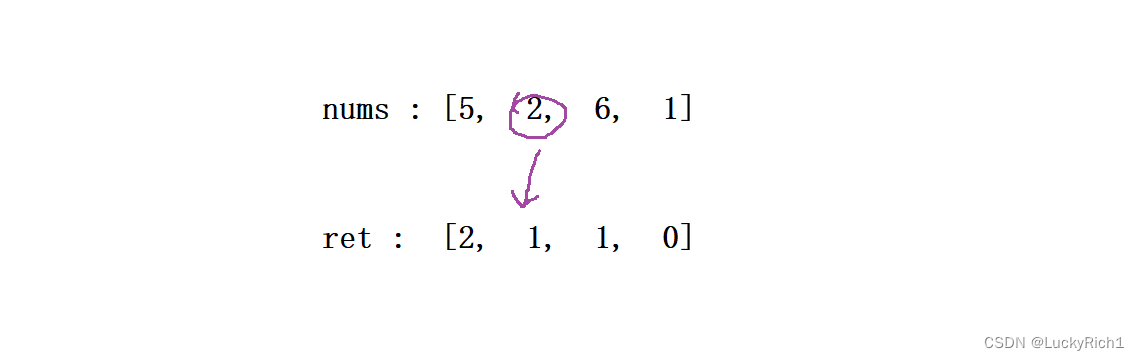
因此當算出nums[cur1]右邊有多少個比我小的時候，最終加的結果是這個值對應的原始下標對應的值 += right - cur2 + 1。

所以我們著重要解決的問題是，當我們找到當前位置的值右邊有多少個比我小的時候，我要能找到這個值得原始下標。 找到 nums 中當前元素的原始下標是多少？ 因為排完序后原本數對應的下標就已經亂了！當前位置cur1 可能并不是我真實的下標。

可能你會想到用哈希表，但是，如果數組里面有重復元素，就難搞了。所以我們直接搞一下和原始數組大小的index數組，記錄當前元素的原始下標。不管nums里面怎么辦，就把index和nums里面對應的值綁定！nums里面的值動，index里面的值也動! 這樣就可以通過index里面值找到當前值原始下標在哪里，然后就可以加了。

回歸上面的問題 把nums[cur1] 對應的 index(下標) 里面的 ret += right - cur2 +1 就可以變成這樣 ret[index[cur1]] += ret += right - cur2 +1。

當歸并排序移動nums時，我們要合并兩個有序數組，別忘記我們需要一個tmp輔助數組幫助我們合并。那如何讓nums合并，index也同步綁定呢？ 因此需要兩個tmp輔助數組！

class Solution {vector<int> ret; vector<int> tmpNum;vector<int> tmpIndex;vector<int> index; // 記錄 nums 中當前元素的原始下標
public:vector<int> countSmaller(vector<int>& nums) {int n = nums.size();ret.resize(n);tmpNum.resize(n);tmpIndex.resize(n);index.resize(n);for(int i = 0; i < n; ++i) index[i] = i; // 初始化 index 數組Mergesort(nums, 0, n - 1);return ret;}void Mergesort(vector<int>& nums, int left, int right){if(left >= right) return;// 1. 根據中間點,劃分區間int mid = left + (right - left) / 2;//[left, mid] [mid+1, right]// 2. 先處理左右兩部分Mergesort(nums, left, mid);Mergesort(nums, mid + 1, right);// 3. 處理一左一右的情況int cur1 = left, cur2 = mid + 1, i = 0;while(cur1 <= mid && cur2 <= right) // 降序{if(nums[cur1] <= nums[cur2]){tmpNum[i] = nums[cur2];tmpIndex[i++] = index[cur2++];}else{ret[index[cur1]] += right - cur2 + 1;tmpNum[i] = nums[cur1];tmpIndex[i++] = index[cur1++];}}// 4.處理剩下排序過程while(cur1 <= mid){tmpNum[i] = nums[cur1];tmpIndex[i++] = index[cur1++];}while(cur2 <= right){tmpNum[i] = nums[cur2];tmpIndex[i++] = index[cur2++];}for(int i = left; i <= right; ++i){nums[i] = tmpNum[i - left];index[i] = tmpIndex[i- left];}}
};

4.翻轉對

題目鏈接：493. 翻轉對

題目分析：

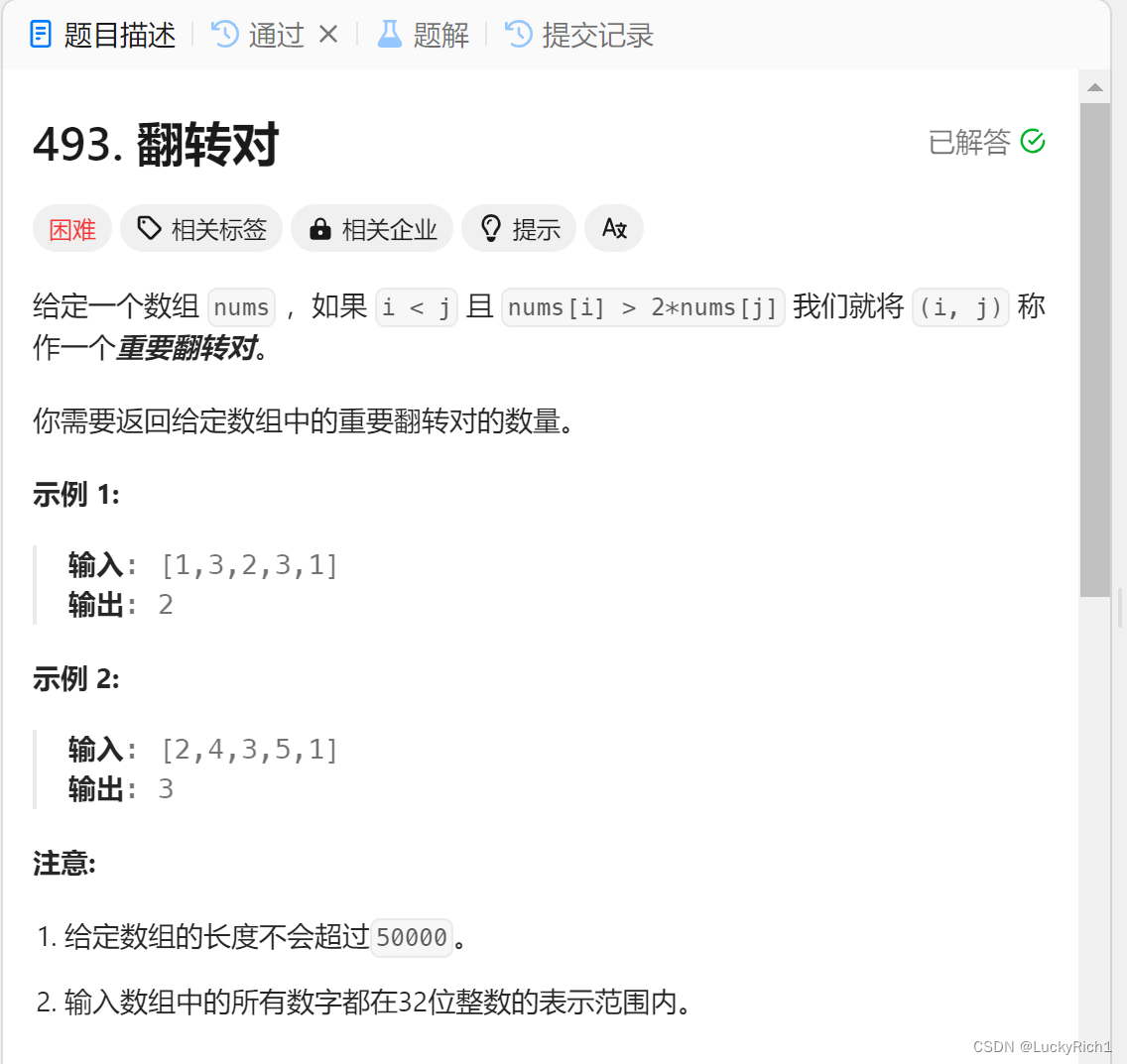
當 i < j 且 nums[i] > 2*nums[j]，才是翻轉對。

算法原理：

解法：分治

這個問題你會發現和求逆序對非常相似的，想求整個數組的翻轉對，先求左半部分的翻轉對記為a，在求右半部分的翻轉對記為b，然后求一左一右的翻轉對記為c。a+b+c就是整個數組的翻轉對。

這個就有個致命的問題，逆序對的題和歸并排序完美契合，僅需比較
i < j，nums[i] > nums[j] 。但是這道題要比較的是 i < j，nums[i] > 2 * nums[j]。這個時候就不能按照歸并排序的流程求翻轉對了，我們要重新想一個策略來求翻轉對。

我們依舊用的是分治的策略來解決，但是并不是用的是歸并排序里面的一個過程來解決我們的問題，我們是在歸并排序之前來計算翻轉對個數。因為我們要利用兩個區間有序的性質，我們可以在一次歸并中用O(N)的時間復雜度搞定這一層的翻轉對的個數

計算翻轉對

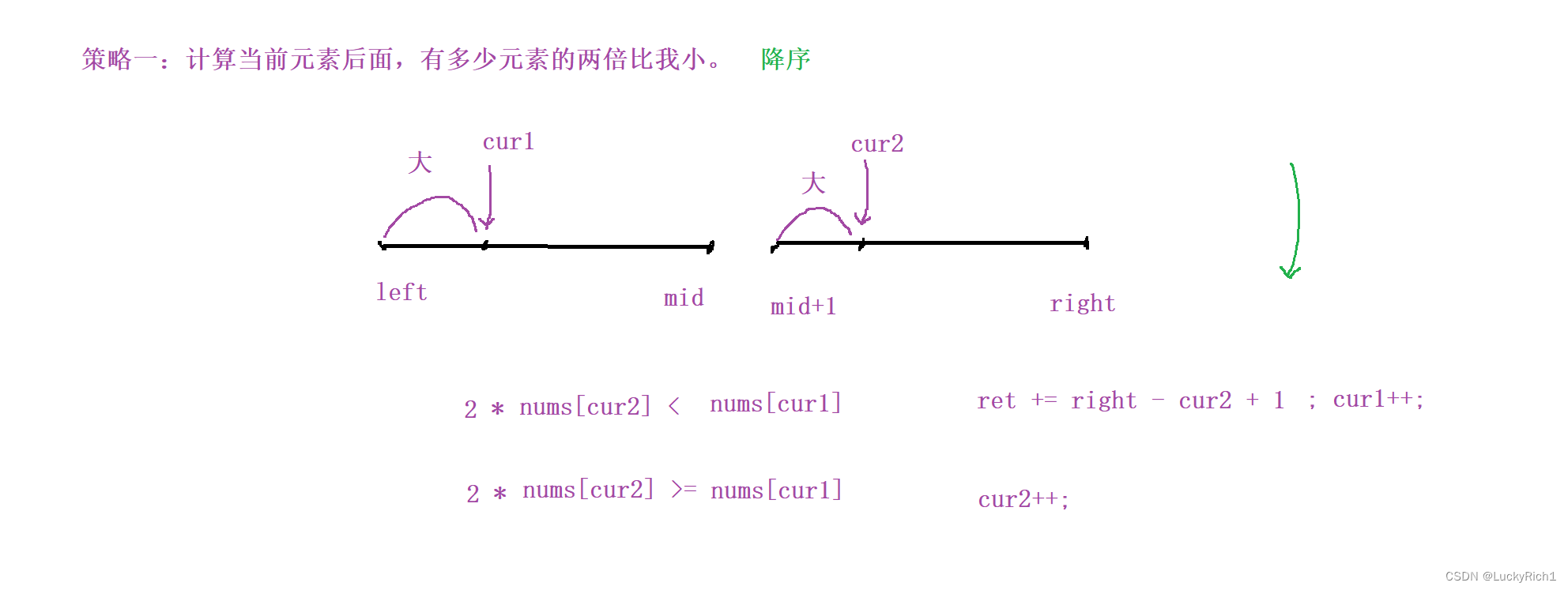
策略一：計算當前元素后面，有多少元素的兩倍比我小。 降序
固定cur1

整個數組都是降序的，固定cur1，當 2 * nums[cur2] >= nums[cur1] cur2往后移，
當 2 * nums[cur2] < nums[cur1] ，因為是降序的，cur2后面一堆元素2倍都比cur1小，所以 ret += right - cur2 +1， cur1的翻轉對都找完了所以往后移動就行了。注意cur2此時是不用回溯的！因為數組是降序的，cur2之前的元素都比cur1還沒有移動的2倍大，cur1往后走一步元素變小了，那cur2之前不就比當前cur1位置更大嘛，所以不用回溯，如果回溯時間復雜度 計算翻轉對就是O(n^2)，那整體時間復雜度就變成O(n ^2 logn)。直到cur1到尾或者cur2到尾就結束了。

計算翻轉對：利用單調性，使用同向雙指針。

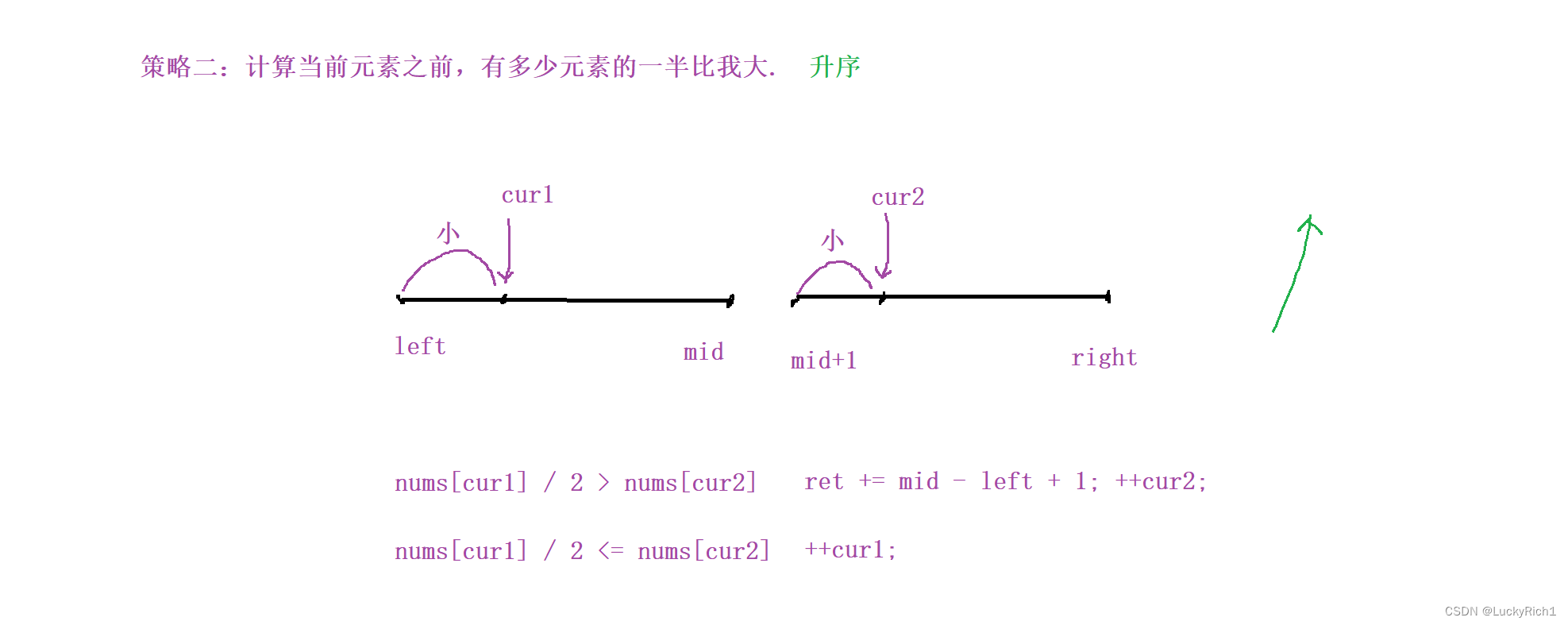
策略二：計算當前元素之前，有多少元素的一半比我大。 升序
固定cur2

整個數組都是升序的，固定cur2，當 nums[cur1] / 2 <= nums[cur1] cur1往后移，
當 nums[cur1] / 2 > nums[cur2] ，因為是升序的，cur1后面一堆元素的一半都比cur2大，所以 ret += mid - left +1， cur2的翻轉對都找完了所以往后移動就行了。此時cur1也不需要回溯。因為是數組是升序的，cur2往后走一步是變大的，cur1還沒有往后移動之前前面的元素一半都比cur2小，現在cur往后走一步變大，肯定比cur1還沒有往后移動之前更大，所以cur1不需要回溯。

注意上面只是計算翻轉對，別忘記還要還要合并兩個有序數組。

降序

class Solution {vector<int> tmp;
public:int reversePairs(vector<int>& nums) {int n = nums.size();tmp.resize(n);return Mergesort(nums, 0, n - 1);}int Mergesort(vector<int>& nums, int left, int right){if(left >= right) return 0;int ret = 0;// 1. 選擇中間點將數組劃分區間int mid = (left + right) >> 1;// 2. 先計算左右兩側的翻轉對ret += Mergesort(nums, left, mid);ret += Mergesort(nums, mid + 1, right);// 3. 先計算翻轉對的數量int cur1 = left, cur2 = mid + 1; while(cur1 <= mid && cur2 <= right)//降序{//if(2 * nums[cur2] < nums[cur1]) //乘法溢出 改成 除法if(nums[cur2] < nums[cur1] / 2.0){ret += right - cur2 + 1;cur1++;}else cur2++;}// 4. 合并兩個有序數組cur1 = left, cur2 = mid + 1;int i = left;while(cur1 <= mid && cur2 <= right){if(nums[cur2] < nums[cur1]) tmp[i++] = nums[cur++];else tmp[i++] = nums[cur2++];}while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];for(int j = left; j <= right; ++j) nums[j] = tmp[j];return ret;     }
};

升序

class Solution {vector<int> tmp;
public:int reversePairs(vector<int>& nums) {int n = nums.size();tmp.resize(n);return Mergesort(nums, 0, n - 1);}int Mergesort(vector<int>& nums, int left, int right){if(left >= right) return 0;int ret = 0;// 1. 選擇中間點將數組劃分區間int mid = (left + right) >> 1;// 2. 先計算左右兩側的翻轉對ret += Mergesort(nums, left, mid);ret += Mergesort(nums, mid + 1, right);// 3. 先計算翻轉對的數量int cur1 = left, cur2 = mid + 1; while(cur1 <= mid && cur2 <= right)//升序{//if(2 * nums[cur2] < nums[cur1]) //乘法溢出 改成 除法if(nums[cur2] < nums[cur1] / 2.0){ret += mid - cur1 + 1;cur2++;}else cur1++;}// 4. 合并兩個有序數組cur1 = left, cur2 = mid + 1;int i = left;while(cur1 <= mid && cur2 <= right){if(nums[cur2] < nums[cur1]) tmp[i++] = nums[cur2++];else tmp[i++] = nums[cur1++];}while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];for(int j = left; j <= right; ++j) nums[j] = tmp[j];return ret;   }
};