集成學習（三）GBDT 梯度提升樹

前面學習了：集成學習（二）Boosting-CSDN博客

梯度提升樹：GBDT-Gradient Boosting Decision Tree

一、介紹

作為當代眾多經典算法的基礎，GBDT的求解過程可謂十分精妙，它不僅開創性地舍棄了使用原始標簽進行訓練的方式，同時還極大地簡化了Boosting算法的運算流程，讓Boosting算法本該非常復雜的運算流程變得清晰簡潔。GBDT的數學流程非常簡明、美麗，同時這一美麗的流程也是我們未來所有Boosting高級算法的數學基礎。與任意Boosting算法一致，對GBDT我們需要回答如下問題：

損失函數 $L(x,y)$ ?的表達式是什么？損失函數如何影響模型構建？
弱評估器? $f(x)$ ?是什么，當下boosting算法使用的具體建樹過程是什么？
綜合集成結果? $H(x)$ ?是什么？集成算法具體如何輸出集成結果？

同時，還可能存在其他需要明確的問題，例如：

是加權求和嗎？如果是，加權求和中的權重如何求解？
訓練過程中，擬合的數據 $X$ 與 $y$ 分別是什么？

回顧Boosting算法的基本指導思想，我們來梳理梯度提升樹回歸算法的基本流程。雖然Boosting理論很早就被人提出，但1999年才是GBDT算法發展的高潮。1999年，有四篇論文橫空出世：

《貪心函數估計：一種梯度提升機器》
Friedman, J. H. (February 1999). "Greedy Function Approximation: A Gradient Boosting Machine"

《隨機梯度提升》
Friedman, J. H. (March 1999). "Stochastic Gradient Boosting"

《梯度下降式提升算法》
Mason, L.; Baxter, J.; Bartlett, P. L.; Frean, Marcus (1999). "Boosting Algorithms as Gradient Descent"

《函數空間中的梯度下降式提升算法》
Mason, L.; Baxter, J.; Bartlett, P. L.; Frean, Marcus (May 1999). "Boosting Algorithms as Gradient Descent in Function Space"

GBDT算法是融合了上述4篇論文思想的集大成之作，為了保持一致，使用與前文不同的數學符號。

二、數學過程

假設現有數據集，含有形如 $\left ( x_{i}, y_{i} \right )$ 的樣本 $M$ 個， $i$ 為任意樣本的編號，單一樣本的損失函數為 $l\left ( y_{i}, H\left ( x_{i} \right ) \right )$ ，其中? $H\left ( x_{i} \right )$ 是 $i$ 號樣本在集成算法上的預測結果，整個算法的損失函數為? $L\left ( y, H( x ) \right )$ ，且總損失等于全部樣本的損失之和： $L(y,H(x))=\sum_{i}^{}l\left ( y_{i}, H\left ( x_{i} \right ) \right )$ 。同時，弱評估器為回歸樹 ，總共學習 $T$ 輪。則GBDT回歸的基本流程如下所示：

1、初始化數據迭代的起點 $H_{0}(x)$ 。sklearn當中，我們可以使用0、隨機數或者任意算法的輸出結果作為 $H_{0}(x)$ ?，但在最初的論文中，Friedman定義了如下公式來計算? $H_{0}(x)$ ?：

其中? $y_{i}$ ?為真實標簽，?C?為任意常數。以上式子表示，找出令 $\sum_{i}^{M}l\left ( y_{i}, C \right )$ ?最小的常數?C?值，并輸出最小的? $\sum_{i}^{M}l\left ( y_{i}, C \right )$ 作為 $H_{0}(x)$ 的值。需要注意的是，由于 $H_{0}(x)$ 是由全部樣本的 $l$ 計算出來的，因此所有樣本的初始值都是 $H_{0}(x)$ ，不存在針對某一樣本的單一初始值。

開始循環，for t in 1,2,3...T：

2、在現有數據集?N?中，抽樣?M?subsample?個樣本，構成訓練集 $N_{t}$
3、對任意一個樣本 $i$ ?，計算偽殘差（pseudo-residuals） $r_{it}$ ，具體公式為：

不難發現，偽殘差是一個樣本的損失函數對該樣本在集成算法上的預測值求導后取負的結果，并且在進行第 $t$ 次迭代、計算第 $t$ 個偽殘差時，我們使用的前 $t-1$ 次迭代后輸出的集成算法結果。在 $t=1$ 時，所有偽殘差計算中的 $H_{t-1}(x_{i})$ ?都等于初始 $H_{0}(x)$ ，在 $t> 0$ 時，每個樣本上的? $H_{t-1}(x_{i})$ 都是不同的取值。

4、求解出偽殘差后，在數據集? $\left ( x_{i},r_{it} \right )$ 上按照CART樹規則建立一棵回歸樹 $f_{t}$ ，訓練時擬合的標簽為樣本的偽殘差 $r_{it}$ ?。

5、將數據集 $N_{t}$ 上所有的樣本輸入 $f_{t}$ 進行預測，對每一個樣本，得出預測結果 $f_{t}\left ( x_{i} \right )$ 。在數學上我們可以證明，只要擬合對象是偽殘差? $r_{it}$ ，則 $f_{t}\left ( x_{i} \right )$ 的值一定能讓損失函數最快減小。

6、根據預測結果 $f_{t}\left ( x_{i} \right )$ 迭代模型，具體來說：

假設輸入的步長為 $\eta$ ，則 $H_{t}(x)$ 應該為：

對整個算法則有：

7、循環結束，輸出? $H_{T}(x)$ ?的值作為集成模型的輸出值。

三、初始化?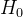 $H_{0}$ 過程中的常數C是什么？

在最初的論文中，Friedman定義了如下公式來計算 $H_{0}$ ?:

其中? $y_{i}$ ?為真實標簽，?C?為任意常數。以上式子表示，找出令 $\sum_{i}^{M}l\left ( y_{i}, C \right )$ ?最小的常數?C?值，并輸出最小的? $\sum_{i}^{M}l\left ( y_{i}, C \right )$ 作為 $H_{0}(x)$ 的值。在剛觀察這個式子時，大家可能很難理解?C?這個常數的作用，但這個式子實際上很簡單。

首先， $l$ 是損失函數，損失函數衡量兩個自變量之間的差異，因此 $l\left ( y_{i}, C \right )$ 衡量樣本 $i$ 的真實標簽 $y_{i}$ ?與常數C之間的差異，因此 $l\left ( y_{i}, C \right )$ 是所有樣本的真實標簽與常數C之間的差異之和。現在我們要找到一個常數C，令所有樣本的真實標簽與常數C的差異之和最小，請問常數C是多少呢？這是一個典型的求極值問題，只需要對 $\sum_{i}^{M}l\left ( y_{i}, C \right )$ ?求導，再令導數為0就可以解出令 $\sum_{i}^{M}l\left ( y_{i}, C \right )$ 最佳的C。假設? $l$ ?是squared_error，每個樣本的平方誤差，則有：

對上述式子求導，并令一階導數等于0：

所以：

可知，當L是平方誤差squared error時，令? $l\left ( y_{i}, C \right )$ ?最小的常數C就是真實標簽的均值。因此，式子? $H_{0}=argmin_{C}\sum_{i}^{M}l\left ( y_{i}, C \right )$ 的本質其實是求解? $C=mean\left ( y_{i} \right )$ 時的損失函數，并以此損失函數作為? $H_{0}$ 的值。當然，如果我們選擇了其他的損失函數，我們就需要以其他方式（甚至梯度下降）進行求解，?C?的值可能也就不再是均值了。

四、為什么擬合偽殘差可以令損失函數最快地減小

從直覺上來看，擬合偽殘差可以降低 $H_{t}\left ( x_{i} \right )$ 與? $y_{i}$ ?之間的差異，從而降低整體損失函數的值，但這個行為在數學上真的可行嗎？畢竟，GBDT可以使用任意可微函數作為損失函數，不同損失函數求導后的結果即便與殘差相似，也未必能代替真正的殘差的效果。因此，不僅在直覺上需要理解擬合偽殘差的作用，我們還需要從數學上證明：只要擬合對象是偽殘差 $r_{it}$ ，則弱評估器的輸出值? $f_{t}\left ( x_{i} \right )$ ?一定是讓損失函數減小最快的值。

我們可以對損失函數進行泰勒展開。對單一樣本而言，我們有損失函數 $l(y_{i},H_{t-1}(x_{i})+f_{t}(x_{i}))$ ，其中? $y_{i}$ 是已知的常數，因此損失函數可以被看做是只有 $H_{t-1}(x_{i})+f_{t}(x_{i})$ 一個自變量的函數，從而簡寫為? $l(H_{t-1}(x_{i})+f_{t}(x_{i}))$ 。

根據一階泰勒展開，已知：

該式子中 $H_{t-1}(x_{i})$ ?是常數，因此第一部分 $l(H_{t-1}(x_{i}))$ 也是一個常數。同時，第二部分由導數和 $f_{t}$ 組成，其中導數就是梯度，可以寫作? $g_{i}$ ?，所以式子可以化簡為：

現在，如果要令? $l$ ?最小，? $f_{t}(x_{i})$ ?應該等于多少呢？回到我們最初的目標，找出令損失函數 $l$ 最小的 $f_{t}$ 值：

常數無法被最小化，因此繼續化簡：

現在，? $g_{t}$ 是包含了所有樣本梯度的向量， $f_{t}(x)$ ?是包含了所有樣本在 $f_{t}$ 上預測值的向量，兩個向量對應位置元素相乘后求和，即表示為向量的內積，由尖括號????表示。現在我們希望求解向量內積的最小值、并找出令向量內積最小的 $f_{t}(x)$ 的取值，那就必須先找出 $f_{t}(x)$ 的方向，再找出? $f_{t}(x)$ ?的大小。

1、方向

$f_{t}(x)$ 的方向應該與 $g_{t}$ 完全相反。向量的內積? $\left \langle g_{t} f_{t}(x)\right \rangle=\left |g_{t} \right |\left | f_{t} (x) \right |cos(\alpha)$ ，其中前兩項為兩個向量的模長，?α?是兩個向量的夾角大小。模長默認為整數，因此當且僅當兩個向量的方向完全相反，即夾角大小為180度時，?cos(α)?的值為-1，才能保證兩個向量的內積最小。假設向量 a = [1,2]，向量b是與a的方向完全相反的向量。假設a和b等長，那向量b就是[-1,-2]。因此，與 $g_{t}$ 方向完全相反且等長的向量就是?， $-g_{t}$ ， $f_{t}(x)$ 的方向也正是 $-g_{t}$ 的方向。

2、大小

對于向量a，除了[-1,-2]之外，還存在眾多與其呈180度夾角、但大小不一致的向量，比如[-2,-4], [-0.5,-1]，每一個都可以與向量a求得內積。并且我們會發現，當方向相反時，向量b中的元素絕對值越大，b的模長就越長，向量a與b的內積就越小。因此不難發現，? $\left \langle g_{t} f_{t}(x)\right \rangle$ ?是一個理論上可以取到無窮小的值，那我們的?ft(x)?應該取什么大小呢？答案非常出乎意料：任何大小都無所謂。

回到我們的迭代公式：

無論? $f_{t}(x)$ 的大小是多少，我們都可以通過步長?η?對其進行調整，只要能夠影響? $H(x)$ ，我們就可以影響損失迭代過程中的常數的大小。因此在數學上來說， $f_{t}(x)$ ?的大小可以是 $-g_{t}$ 的任意倍數，這一點在梯度下降中其實也是一樣的。為了方便起見，同時為了與傳統梯度下降過程一致，我們通常讓? $f_{t}(x)$ 就等于一倍的 $-g_{t}$ ，但也有不少論文令? $f_{t}(x)$ 等于其他值的。在GBDT當中：

這就是我們讓GBDT當中的弱評估器擬合偽殘差/負梯度的根本原因。擬合負梯度其實為GBDT帶來了非常多的特點:

首先，通過直接擬合負梯度，GBDT避免了從損失函數找“最優”的過程，即避免了上述證明中求解? $f_{t}=argmin_{f}\sum_{i=1}^{M}l\left ( H_{t-1}(x_{i})+f_{t}(x_{i}) \right )$ ?的過程，從而大大地簡化了計算。

其次，通過擬合負梯度，GBDT模擬了梯度下降的過程，由于結合了傳統提升法Boosting與梯度下降，因此才被命名為梯度提升法（Gradient Boosting）。這個過程后來被稱為函數空間上的梯度下降（Gradient Descent in Function Space），這是視角為Boosting算法的發展奠定了重要的基礎。

最后，最重要的一點是，通過讓弱評估器擬合負梯度，弱評估器上的結果可以直接影響損失函數、保證損失函數的降低，從而指向Boosting算法的根本目標：降低偏差。這一過程避免了許多在其他算法中需要詳細討論的問題：例如，每個弱評估器的權重???是多少，以及弱評估器的置信度如何。

在AdaBoost算法當中，損失函數是“間接”影響弱評估器的建立，因此有的弱評估器能夠降低損失函數，而有的弱評估器不能降低損失函數，因此要在求和之前，需要先求解弱評估器的置信度，然后再給與置信度高的評估器更高的權重，權重???存在的根本意義是為了調節單一弱評估器對???的貢獻程度。但在GBDT當中，由于所有的弱評估器都是能夠降低損失函數的，只不過降低的程度不同，因此就不再需要置信度/貢獻度的衡量，因此就不再需要權重???。