原題鏈接🔗：路徑總和 III
難度：中等????

題目

給定一個二叉樹的根節點 root ，和一個整數 targetSum ，求該二叉樹里節點值之和等于 targetSum 的 路徑 的數目。

路徑 不需要從根節點開始，也不需要在葉子節點結束，但是路徑方向必須是向下的（只能從父節點到子節點）。

示例 1：

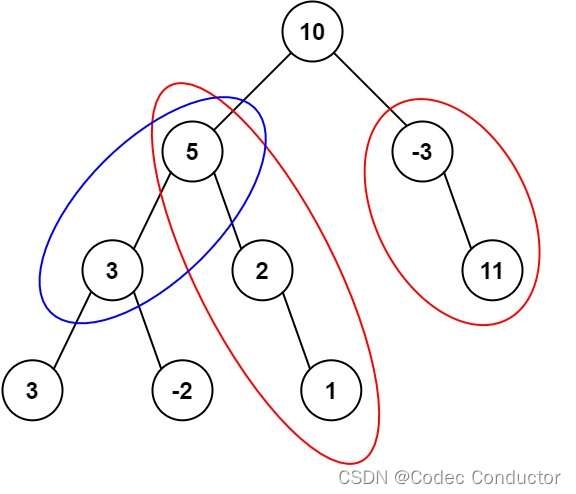
輸入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
輸出：3
解釋：和等于 8 的路徑有 3 條，如圖所示。

示例 2：

輸入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
輸出：3

提示:

• 二叉樹的節點個數的范圍是 [0,1000]
• -10⁹ <= Node.val <= 10⁹
• -1000 <= targetSum <= 1000

題解

什么是深度優先搜索

深度優先搜索（Depth-First Search，簡稱 DFS）是一種用于遍歷或搜索樹或圖的算法。這種算法會盡可能深地搜索樹的分支，當節點 v 的所有可達的鄰接節點都已被探索過，搜索回溯到發現節點 v 的那條邊的起始節點，繼續進行搜索。

深度優先搜索的基本思想是：

1. 從起始節點開始：選擇一個起始節點，將其標記為已訪問。

2. 訪問鄰接節點：從當前節點開始，選擇一個未被訪問的鄰接節點，移動到該節點，并將該節點標記為已訪問。

3. 遞歸搜索：對新到達的節點，重復步驟2，直到找到一個沒有未訪問鄰接節點的節點。

4. 回溯：當當前節點的所有鄰接節點都被訪問過，或者沒有更多的鄰接節點時，回溯到前一個節點，繼續搜索。

5. 終止條件：當所有節點都被訪問過，或者搜索完所有可能的路徑時，搜索結束。

深度優先搜索可以用于多種場景，包括但不限于：

• 連通性問題：確定圖中的節點是否全部連通。
• 拓撲排序：對有向無環圖（DAG）的頂點進行排序。
• 路徑查找：在圖中查找從一個節點到另一個節點的路徑。
• 解決數獨：通過嘗試不同的數字來解決數獨問題。

深度優先搜索通常使用遞歸或顯式的棧來實現。在樹結構中，深度優先搜索可以確保每個節點只被訪問一次，而在圖中，為了避免重復訪問節點，通常需要使用一個集合或數組來跟蹤已訪問的節點。

深度優先搜索的效率取決于圖或樹的結構，以及搜索的具體目標。在最壞的情況下，它可能需要檢查所有可能的節點和邊。

深度優先搜索法

1. 解題思路：

LeetCode 上的 “路徑總和 III” 可以通過深度優先搜索（DFS）來解決。以下是使用 DFS 解決這個問題的步驟：

• 定義遞歸函數：創建一個遞歸函數，該函數接收當前節點、當前路徑和以及目標和。

• 初始化路徑和：在遞歸函數中，更新當前路徑和，即從根節點到當前節點的和。

• 檢查當前節點：如果當前節點是葉子節點（即沒有左右子節點），檢查當前路徑和是否等于目標和。如果是，增加路徑計數。

• 遞歸遍歷子樹：對當前節點的左右子節點進行遞歸調用，更新路徑和并傳遞給子樹。

• 回溯：在遞歸調用結束后，需要回溯以撤銷當前節點的選擇，這通常通過減少當前路徑和來實現。

• 路徑計數：在遞歸過程中，除了檢查當前路徑和是否等于目標和外，還需要將當前路徑和與目標和做差，然后檢查差值是否存在于一個哈希表中，這個哈希表用于存儲從根到當前節點的路徑和。

• 使用哈希表優化：在遞歸過程中，如果當前節點的路徑和減去目標和的結果存在于哈希表中，那么從當前節點到葉子節點的路徑中，存在一條路徑的和等于目標和。

• 返回結果：在遞歸的底部，返回路徑計數。

2. 復雜度：時間復雜度O(N²)，空間復雜度O(N)。

3. c++ demo：

#include <iostream>
#include <unordered_map>using namespace std;// 定義二叉樹的節點結構
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};class Solution {
public:int rootSum(TreeNode* root, int targetSum) {if (!root) {return 0;}int ret = 0;if (root->val == targetSum) {ret++;}ret += rootSum(root->left, targetSum - root->val);ret += rootSum(root->right, targetSum - root->val);return ret;}int pathSum(TreeNode* root, int targetSum) {if (!root) {return 0;}int ret = rootSum(root, targetSum);ret += pathSum(root->left, targetSum);ret += pathSum(root->right, targetSum);return ret;}
};int main() {// 構建一個簡單的二叉樹TreeNode* root = new TreeNode(10);root->left = new TreeNode(5);root->right = new TreeNode(-3);root->left->left = new TreeNode(3);root->left->right = new TreeNode(2);root->right->right = new TreeNode(11);root->left->right->right = new TreeNode(1);root->left->left->left= new TreeNode(3);root->left->left->right = new TreeNode(-2);// 創建 Solution 對象Solution solution;int result = solution.pathSum(root, 8); // 尋找路徑和為8的路徑數量cout << "Number of paths with sum 8: " << result << endl;// 釋放二叉樹占用的內存delete root->left->left->right;delete root->left->left->left;delete root->left->right->right;delete root->left->left;delete root->left->right;delete root->right->right;delete root->left;delete root->right;delete root;return 0;
}

• 輸出結果:

Number of paths with sum 8: 3

4. 代碼倉庫地址：rootSum