多項式回歸原理詳解
????????多項式回歸(Polynomial Regression)是線性回歸(Linear Regression)的一種擴展形式。它通過在輸入變量上添加高次項來擬合非線性關系。雖然多項式回歸本質上還是線性模型,但它允許模型在輸入特征的多項式基礎上進行線性擬合,從而捕捉復雜的非線性關系。
1. 多項式回歸的數學表達式
????????假設我們有一個輸入特征 x?和輸出變量 y,多項式回歸模型可以表示為:
????????????????????????y=β0+β1x+β2x2+β3x3+?+βnxn+?
????????其中,β0,β1,β2,…,βn是模型的參數,n?是多項式的階數,?是誤差項。
2. 多項式回歸的步驟
-
選擇多項式的階數:選擇合適的多項式階數 n?是模型擬合的關鍵。階數過低可能會導致欠擬合,階數過高則可能導致過擬合。
-
構建多項式特征:將輸入特征擴展為多項式特征。例如,對于一個一維特征 x,構建的特征矩陣為
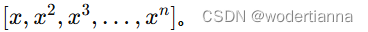
-
擬合模型:使用線性回歸方法在多項式特征上進行擬合。
-
評估模型:通過均方誤差(MSE)等指標評估模型的性能。
Python代碼示例
????????以下是一個完整的Python代碼示例,用于實現多項式回歸。我們將使用scikit-learn庫來構建和評估模型。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error# 生成一些示例數據
np.random.seed(0)
x = 2 - 3 * np.random.normal(0, 1, 100)
y = x - 2 * (x ** 2) + np.random.normal(-3, 3, 100)# 將數據轉化為二維數組
x = x[:, np.newaxis]
y = y[:, np.newaxis]# 可視化原始數據
plt.scatter(x, y, s=10)
plt.title("Original Data")
plt.show()# 創建多項式特征(例如,二次多項式)
poly = PolynomialFeatures(degree=2)
x_poly = poly.fit_transform(x)# 創建線性回歸模型并在多項式特征上進行擬合
model = LinearRegression()
model.fit(x_poly, y)# 預測結果
y_pred = model.predict(x_poly)# 可視化擬合結果
plt.scatter(x, y, s=10, label='Original data')
plt.plot(x, y_pred, color='r', label='Fitted polynomial')
plt.title("Polynomial Regression (degree=2)")
plt.legend()
plt.show()# 打印模型參數和均方誤差
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)
print("Mean Squared Error:", mean_squared_error(y, y_pred))# 嘗試不同的多項式階數
degrees = [1, 2, 3, 4, 5]
for degree in degrees:poly = PolynomialFeatures(degree=degree)x_poly = poly.fit_transform(x)model = LinearRegression()model.fit(x_poly, y)y_pred = model.predict(x_poly)plt.scatter(x, y, s=10, label='Original data')plt.plot(x, y_pred, label=f'Degree {degree}')plt.title(f"Polynomial Regression (degree={degree})")plt.legend()plt.show()print(f"Degree {degree} - Coefficients:", model.coef_)print(f"Degree {degree} - Intercept:", model.intercept_)print(f"Degree {degree} - Mean Squared Error:", mean_squared_error(y, y_pred))
?
代碼解釋
- 數據生成:我們生成了一些具有二次關系的示例數據,其中加入了隨機噪聲。
- 數據預處理:將數據轉化為二維數組,以便后續處理。
- 多項式特征構建:使用
PolynomialFeatures類構建多項式特征,這里示例為二次多項式。 - 模型擬合:使用
LinearRegression類在多項式特征上進行擬合。 - 結果預測和可視化:預測結果并繪制原始數據和擬合曲線,便于觀察擬合效果。
- 模型評估:打印模型參數(系數和截距)和均方誤差(MSE)以評估模型性能。
- 不同階數的多項式回歸:嘗試不同的多項式階數(1到5),并分別進行擬合和評估。
?


vue2)












)



