二叉樹順序結構及鏈式結構

一.二叉樹的順序結構

1.定義：使用數組存儲數據，一般使用數組只適合表示完全二叉樹，此時不會有空間的浪費

注：二叉樹的順序存儲在邏輯上是一顆二叉樹，但是在物理上是一個數組，此時需要程序員自己想清楚調整數據時應該怎樣調整

2.堆

(1)定義：集合中所有元素按照完全二叉樹的順序存儲在一個一維數組中，并滿足Ki<=K2*i+1且K2*i+2(或Ki<=K2*i+1且K2*i+2)的規律，則稱之為堆

(2)性質：

1>堆中某個節點的值總是不大于(或不小于)其父節點的值

2>堆是一顆完全二叉樹

3>大堆：任何一個父節點的值>=孩子的值

? ? 小堆：任何一個父節點的值<=孩子的值

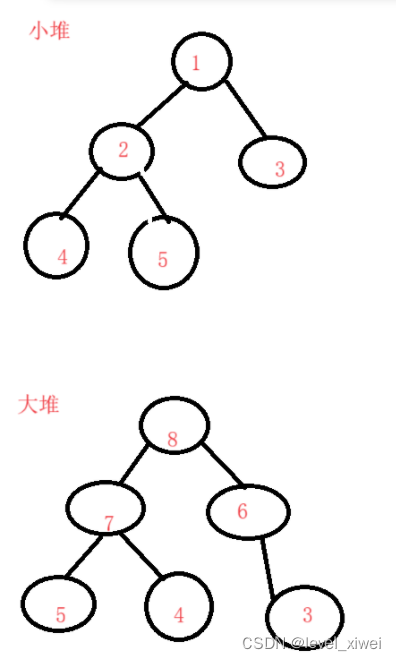
(3)堆的實現(以小堆為例)

1>堆的結構體定義：數組指針(用于存儲數據),有效數據個數，空間容量大小

typedef int HeapDataType;
typedef struct Heap
{HeapDataType* a;//數組指針int size;//有效數據個數int capacity;//有效空間大小
}HP;

2>堆的初始化：

//堆的初始化
void HPInit(HP* ph)
{assert(ph);ph->a = NULL;ph->size = ph->capacity = 0;
}

3>堆的銷毀：

//堆的銷毀
void HPDestory(HP* ph)
{assert(ph);free(ph->a);ph->a = NULL;ph->size = ph->capacity = 0;
}

4>向堆中插入數據：

**思路：將數據插在原數據的最后面，在不斷向上調整以保證插入數據后仍為小堆?

**畫圖解釋

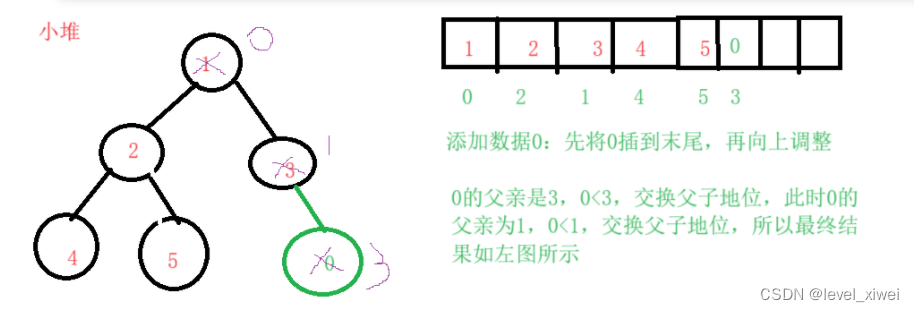
**代碼實現

//向堆內插入數據
void HPPush(HP* ph, HeapDataType x)
{assert(ph);//判斷是否需要增容if (ph->size == ph->capacity){int newcapacity = ph->capacity * 2 == 0 ? 4 : ph->capacity * 2;HeapDataType* tmp = (HeapDataType*)realloc(ph->a, sizeof(HeapDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");return;}ph->a = tmp;ph->capacity = newcapacity;}ph->a[ph->size] = x;ph->size++;AdjustUp(ph->a, ph->size-1);}

5>向上調整數據：

思路：找孩子的父親，判斷父親是否大于孩子，若大于則交換父子地位，繼續向上調整

?注：由于堆是完全二叉樹，一個父親最多有兩個孩子，所以父親的下標應該是孩子的下標減一再除以2，即parent=(child-1)/2;

//向上調整
void AdjustUp(HeapDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent= (child - 1) / 2;}else{break;}}
}

6>刪除根部數據：

思路：先交換根部數據和最后一個數據，再刪除根部數據，同時將最后一個數據向下調整以保證刪除后的堆仍為小堆

//刪除堆頂數據(根位置)
void HPPop(HP* ph)
{assert(ph);Swap(&ph->a[0], &ph->a[ph->size - 1]);ph->size--;AdjustDown(ph->a, ph->size, 0);
}

7>向下調整數據：

**思路：先找左右孩子中較小的那個孩子，與父親相比，若父親大于孩子，則交換父子地位，繼續向下調整

注：由于堆是完全二叉樹，一個父親最多有兩個孩子，所以左孩子的下標應該是父親的下標乘以2再加1，即child=parent*2+1;

**畫圖解釋

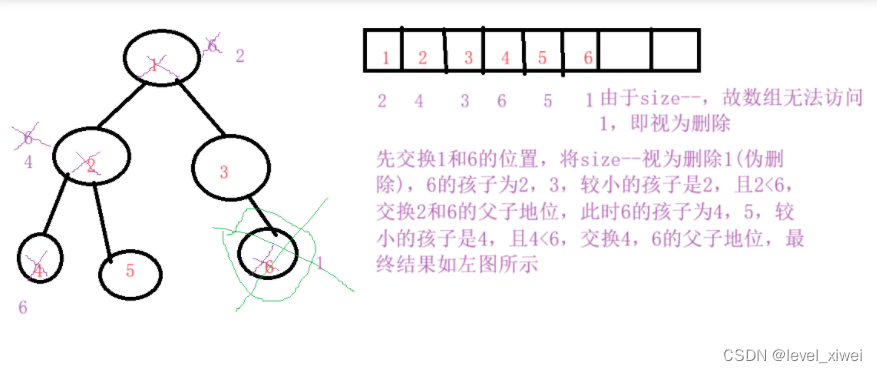
**代碼實現

//向下調整
void AdjustDown(HeapDataType* a, int size, int parent)
{//默認左孩子小int child = parent * 2 + 1;while (child < size){//找左右孩子中小的那一個if ((child+1) < size && a[child+1] < a[child]){child ++;}if (a[parent] > a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}

(4)堆的應用

1>堆排序

1.1)思路：注：降序：建小堆，升序建大堆

? ? ? ? ? ? ?將數組中的元素建堆，交換最后的數據與首位數據，并進行向下調整，讓size--，循環操? ? ? ? ? ? ? ? ?作，直至完成排序

1.2)時間復雜度：O（N*log N）

1.3)畫圖解釋：

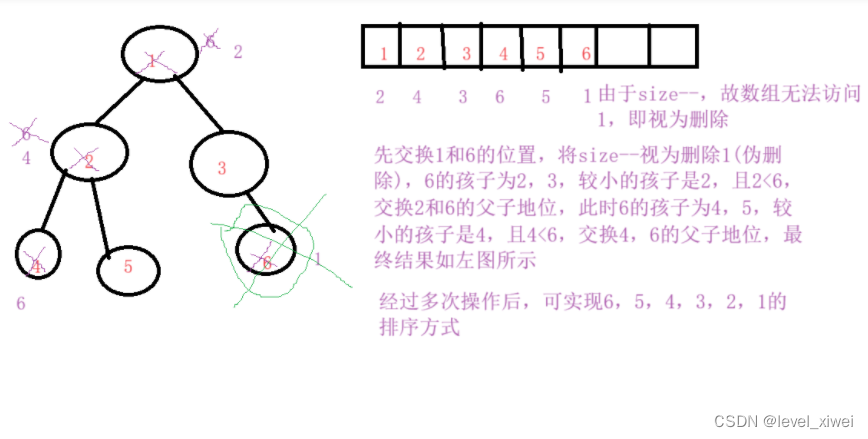
1.4)代碼實現

void HeapSort(int* a, int size)
{//將數組建堆for (int i = 1; i < size; i++){AdjustUp(a, i);}int end = size - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}

2>TOP_K(以求前K個最大的數據為例)

2.1)定義：求出數據中前K個最大的數據（或前K個最小的數據）

2.2)思路：

思路一：創建一個含N個節點的大堆，PopK次，即可獲取前K個最大的數據

? ? ? ? ? ? ? 弊端：當N非常大時，在創建節點時需要占用大量的內存

思路二：建一個含K個節點的小堆，將剩余的N-K個數據與堆頂數據相比，若大于堆頂數據則入? ? ? ? ? ? ? ? ? ? 堆進行向下調整，否則進行下一個比較

注：思路二更優，效率高

2.3)代碼實現

void TOP_K(int* a,int n,int k) 
{//在文件中讀取數據const char* fp = "data.txt";FILE* fout = fopen(fp, "r");if (fout == NULL){perror("fopen fail");return;}//讀取前K個數據for (int i = 0; i < k; i++){fscanf(fout,"%d", &a[i]);}//建小堆for (int i = (k-1-1)/2;i>=0;i--){AdjustDown(a, k, i);}//將剩余的n-k個數據于堆頂數據相比int x = 0;while (fscanf(fout,"%d",&x)!=EOF){if (a[0]<x){a[0] = x;AdjustDown(a, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", a[i]);}printf("\n");
}

2.4)數據驗證

思路：將N的節點的數據模上N，是他們處于小于N的狀態，在隨機挑K個數據將他們調大于N，若在選出來的K個數據為大于N的數據，則說明該程序執行的是選取前K個最大的數據的指令

二.二叉樹的鏈式結構(以二叉鏈表為例)

注：在二叉樹的實現中多用遞歸來達到一層一層向下查找的目的(所以讀者需要熟練掌握遞歸的相關知識)

1.定義：用鏈表表示一顆二叉樹，即用鏈表表示元素之間的邏輯關系

2.二叉樹節點的定義：該節點內存儲的數據，指向左孩子的指針，指向右孩子的指針

typedef int BTNodeData;
typedef struct BinaryTreeNode
{BTNodeData val;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;

3.二叉樹的創建(根據前序遍歷來創建二叉樹)：

以數組abd##e#h##cf##g##構建二叉樹

1>思路：1)若當前數據為#，則返回NULL；

? ? ? ? ? ? ? ?2)否則開辟一個二叉樹節點root，將該數據賦給val,給左，右孩子賦值，通過調用函數遞? ? ? ? ? ? ? ? ?歸實現

2>代碼實現：

//創建二叉樹
BTNode* BTCreate(BTNodeData* a, int* pi)
{if (a[*pi] == ‘#’){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->val = a[*pi];(*pi)++;root->left = BTCreate(a,pi);root->right = BTCreate(a, pi);return root;
}

4.二叉樹的前序遍歷：

1>訪問順序：根，左子樹，右子樹

2>思路：如果根為空，打印N，什么都不返回；否則先打印根的值，再調用該函數，將左子樹的地址作為參數，然后調用該函數，將右子樹的地址作為參數，利用遞歸實現前序遍歷

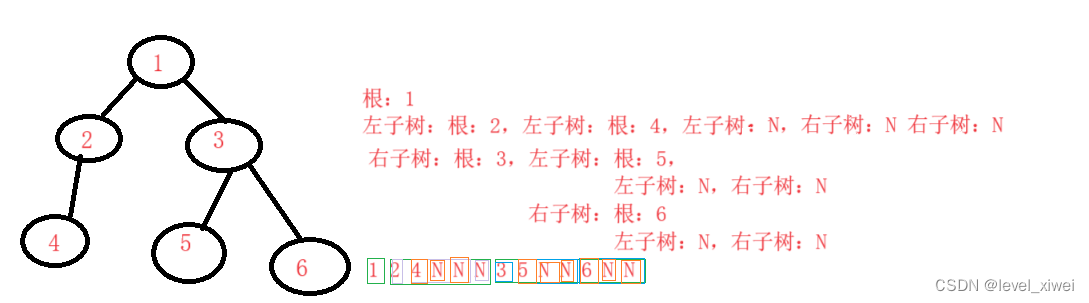
3>代碼實現

//前序遍歷
void PreOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->val);PreOrder(root->left);PreOrder(root->right);
}

5.二叉樹的中序遍歷

1>訪問順序：左子樹，根，右子樹

2>思路：與前序遍歷類似

3>代碼實現

//中序遍歷
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}

6.二叉樹的后序遍歷

1>訪問順序：左子樹，右子樹，根

2>思路：與前序遍歷類似

3>代碼實現

//后序遍歷
void PostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}

7.二叉樹的層序遍歷

1>思路：利用隊列，讓上一層的節點先入隊列，在刪除他們時，帶進去下一層，若節點為空不進隊列

2>代碼實現：

//層序遍歷
void BTLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->val);//當節點不為空時入隊列if (front->left){QueuePush(&q, front->left);}if(front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestory(&q);
}

8.二叉樹的節點個數

1>思路：1)如果根節點為空，返回0；

? ? ? ? ? ? ? ?2)否則返回左子樹的節點數+右子樹的節點數+1(利用遞歸法實現左右子樹節點數的計算)

2>代碼實現：

//二叉樹節點個數
int BTSize(BTNode* root)
{if (root == NULL){return 0;}return  BTSize(root->left) + BTSize(root->right) + 1;
}

9.二叉樹的葉子節點個數

1>思路：1)如果根為空，返回0；

? ? ? ? ? ? ? ?2)如果左右孩子均為空，返回1；

? ? ? ? ? ? ? ?3)否則返回左子樹葉子數+右子樹葉子數(利用遞歸實現左右子樹葉子數的計算)

2>代碼實現：

//二叉樹葉子節點個數
int BTLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BTLeafSize(root->left) + BTLeafSize(root->right);
}

10.二叉樹第K層節點個數

1>思路：1)如果根為空返回0；

? ? ? ? ? ? ? ?2)如果k==1，返回1；

? ? ? ? ? ? ? ?3)否則返回左子樹的k-1層+右子樹的k-1層

注：將樹一層一層向下壓，直至出現兩種特殊情況

2>代碼實現：

//二叉樹第K層節點個數
int BTLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BTLevelKSize(root->left, k - 1) + BTLevelKSize(root->right, k - 1);
}

11.二叉樹查找值為X的節點

1>思路：1)若根為空，返回空；

? ? ? ? ? ? ? ?2)若根的值等于待查找數據，返回根的地址；

? ? ? ? ? ? ? 3)否則查找左子樹是否有值為X的節點若有返回該節點的地址，否則查找右子樹是否有值? ? ? ? ? ? ? ? ? 為X的節點若有返回該節點的地址，若左右子樹均沒有是否有值為X的節點，則返回空

2>代碼實現：

//二叉樹查找值為X的節點
BTNode* BTFind(BTNode* root, BTNodeData x)
{if (root == NULL){return NULL;}if (root->val == x){return root;}//比較左子樹是否有節點值為xBTNode* ret1 = BTFind(root->left, x);if (ret1!=NULL){return ret1;}//比較右子樹是否有節點值為xBTNode* ret2 = BTFind(root->right, x);if (ret2 != NULL){return ret2;}//左右子樹中均未找到值為x的節點return NULL;
}

12.樹的高度

1>思路：1)若根為空，返回0；

? ? ? ? ? ? ? ?2)否則記錄并分別求左右子樹的高度，哪個值更大哪個即為樹的高度

注：每次都需記錄所求的樹的高度，否則會出現走到上一層忘了下一層的情況，導致反復求某棵樹高度的情況

2>代碼實現：

//二叉樹的高度
int BTHeight(BTNode* root)
{if (root == NULL){return 0;}int HeightLeft = BTHeight(root->left)+1;int HeightRight = BTHeight(root->right)+1;return HeightLeft > HeightRight ? HeightLeft  : HeightRight ;
}

13.二叉樹的銷毀

1>思路：用后序遍歷的思想先銷毀左右子樹，再銷毀根(若先銷毀根，銷毀根后，無法找到左右子樹)

2>代碼實現

//二叉樹的銷毀
void BTDestory(BTNode* root)
{if (root == NULL)return;BTDestory(root->left);BTDestory(root->right);free(root);}

14.判斷二叉樹是否為完全二叉樹

1>思路：無論節點是否為空都入隊列，當檢查到第一個空節點時，開始遍歷后面的節點看是否有非空節點，若有，則不是完全二叉樹，否則是完全二叉樹

2>代碼實現

//二叉樹是否為完全二叉樹
bool BTComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//若第一個空如隊列，跳出循壞，開始遍歷看之后是否有非空節點的存在if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}//遍歷，看是否有非空節點while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueueDestory(&q);return false;}}QueueDestory(&q);return true;
}

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/14509.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/14509.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/14509.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

http流式返回

http流式返回

HTTP流式返回&#xff08;Stream&#xff09;是一種服務器向客戶端傳輸數據的方式允許數據分塊發送而不是一次性發送完畢。 這樣客戶端可以在接收到第一部分數據時就開始處理&#xff0c;而不必等待整個響應完成。 應用場景&#xff1a; 2.1 業務場景&#xff1a;圖表的監聽&a…
閱讀更多...
手動安裝maven依賴到本地倉庫

手動安裝maven依賴到本地倉庫

使用mvn install命令安裝jar包到指定的倉庫。 命令如下&#xff1a; mvn install:install-file -Dmaven.repo.localC:\Users\liyong.m2\repository -DgroupIdcom.aspose -DartifactIdwords -Dversion18.4 -Dpackagingjar -DfileC:\Users\liyong\Desktop\jar\words-18.4.jar 解釋…
閱讀更多...
grafana + Prometheus + node-exporter + pushgateway + alertmanager的監控解決方案

grafana + Prometheus + node-exporter + pushgateway + alertmanager的監控解決方案

業內比較著名的監控解決方案&#xff0c;據筆者所知&#xff0c;大概是三套&#xff1a; 一個是zabbix的解決方案&#xff0c;一個是prometheusgrafana&#xff0c;一個是ELK zabbix比較重&#xff0c;而且原生支持監控SNMP&#xff0c;自帶一個儀表盤&#xff0c;不需要額外…
閱讀更多...
docker redis 持久化

docker redis 持久化

1、拉取redis鏡像 docker pull redis:latest 2、 mkdir /data/redis 3、填充redis.conf文件及根據需求修改相應的配置 ?通過官網地址找到對應版本的配置文件 ?將配置信息復制到redis.conf中 ?常見的修改配置 https://redis.io/docs/latest/operate/oss_and_stack/managem…
閱讀更多...
高仿果汁導航模板

高仿果汁導航模板

參考原文&#xff1a;果汁導航風格模板_1234FCOM專注游戲工具及源碼例子分享 極速云
閱讀更多...
sdut pta 鏈表3(優化)-----7-3 sdut-C語言實驗-鏈表的結點插入

sdut pta 鏈表3(優化)-----7-3 sdut-C語言實驗-鏈表的結點插入

7-3 sdut-C語言實驗-鏈表的結點插入 分數 20 全屏瀏覽 切換布局 作者 馬新娟 單位 山東理工大學 給出一個只有頭指針的鏈表和 n 次操作&#xff0c;每次操作為在鏈表的第 m 個元素后面插入一個新元素x。若m 大于鏈表的元素總數則將x放在鏈表的最后。 輸入格式: 多組輸入。…
閱讀更多...
基于springboot的畢業設計系統的開發源碼

基于springboot的畢業設計系統的開發源碼

風定落花生&#xff0c;歌聲逐流水&#xff0c;大家好我是風歌&#xff0c;混跡在java圈的辛苦碼農。今天要和大家聊的是一款基于springboot的畢業設計系統的開發。項目源碼以及部署相關請聯系風歌&#xff0c;文末附上聯系信息 。 項目簡介&#xff1a; 畢業設計系統能夠實現…
閱讀更多...
學習通高分免費刷課實操教程

學習通高分免費刷課實操教程

文章目錄 概要整體架構流程詳細步驟云上全平臺登錄步驟小結 概要 我之前提到過一個通過瀏覽器的三個腳本就可以免費高分刷課的文章&#xff0c;由于不方便拍視頻進行實操演示&#xff0c;然后寫下了這個實操教程&#xff0c;之前的三個腳本劃到文章末尾 整體架構流程 整體大…
閱讀更多...
窗口函數 | rows between …… and ……

窗口函數 | rows between …… and ……

ROWS BETWEEN ... AND ... 是 SQL 窗口函數中的一個子句&#xff0c;用于定義窗口函數操作的行范圍。窗口函數允許用戶對一組相關的記錄執行計算&#xff0c;這些記錄被稱為窗口。 基本語法 <窗口函數> OVER ( [PARTITION BY <列名>] ORDER BY <列名> [AS…
閱讀更多...
前端基礎入門三大核心之HTML篇 —— SVG的viewBox、width和height：繪制矢量圖的魔法比例尺【含代碼示例】

前端基礎入門三大核心之HTML篇 —— SVG的viewBox、width和height：繪制矢量圖的魔法比例尺【含代碼示例】

前端基礎入門三大核心之HTML篇 —— SVG的viewBox、width和height&#xff1a;繪制矢量圖的魔法比例尺【含代碼示例】 基本概念與作用viewBoxwidth和height 代碼示例與實踐基礎示例動態調整示例 不同角度的使用思路保持比例縮放自動適應容器 實際問題與解決方案結語與討論 在前…
閱讀更多...
華為云之Zabbix監控平臺部署實踐

華為云之Zabbix監控平臺部署實踐

華為云之Zabbix監控平臺部署實踐 一、本次實踐介紹1.1 實踐環境簡介1.3 本次實踐完成目標 二、 相關服務介紹2.1 華為云ECS云服務器介紹2.2 Zabbix介紹 三、環境準備工作3.1 預置實驗環境3.2 查看預置環境信息 四、登錄華為云4.1 登錄華為云4.2 查看ECS狀態4.3 連接ECS彈性云服…
閱讀更多...
力扣HOT100 - 287. 尋找重復數

力扣HOT100 - 287. 尋找重復數

解題思路&#xff1a; 快慢指針 第一步&#xff0c;慢指針每次移動一步&#xff0c;快指針每次移動兩步&#xff0c;直到它們相遇。這一步保證了它們在環中相遇。 接下來&#xff0c;將其中一個指針&#xff08;快指針或慢指針&#xff09;重置到起點&#xff08;即數組的第一…
閱讀更多...
SpringBoot實現郵箱驗證碼

SpringBoot實現郵箱驗證碼

自行創建一個SpringBoot項目 導入SpringBoot所需要的郵箱驗證碼的包 <!--郵件發送--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId><version>2.6.1</version>…
閱讀更多...
前后端部署筆記

前后端部署筆記

windows版&#xff1a; 如果傻唄公司讓用win電腦部署&#xff0c;類似于我們使用筆記本做局域網服務器&#xff0c;社內使用。 1.安裝win版的nginx、mysql、node、jdk等 2.nginx開機自啟參考Nginx配置及開機自啟動&#xff08;Windows環境&#xff09;_nginx開機自啟動 wind…
閱讀更多...
UPPAAL使用方法

UPPAAL使用方法

UPPAAL使用方法 由于剛開始學習時間自動機及其使用方法&#xff0c;對UPPAAL使用不太熟悉&#xff0c;網上能找到的教程很少&#xff0c;摸索了很久終于成功實現一個小例子&#xff0c;所以記錄一下詳細教程。 這里用到的例子參考【UPPAAL學習筆記】1&#xff1a;基本使用示例…
閱讀更多...
專業級潤滑油，一站式批發服務

專業級潤滑油，一站式批發服務

要為機械設備提供持久穩定的動力保障嗎&#xff1f;選擇我們的專業級潤滑油&#xff0c;讓您的設備運轉更順暢&#xff0c;效率更高。 我們專業從事潤滑油批發多年&#xff0c;以優質的產品、合理的價格和完善的服務贏得了廣大客戶的信賴。無論是汽車、機械還是工業設備&#x…
閱讀更多...
【Vue3】env環境變量的配置和使用（區分cli和vite）

【Vue3】env環境變量的配置和使用（區分cli和vite）

原文作者&#xff1a;我輩李想 版權聲明&#xff1a;文章原創&#xff0c;轉載時請務必加上原文超鏈接、作者信息和本聲明。 文章目錄 前言一、env文件二、vue3cli加載env1..env配置2..dev配置&#xff08;其他環境參考&#xff09;3.package.json文件4.使用 三、vue3vite加載e…
閱讀更多...
【html5】03-新表單元素及屬性

【html5】03-新表單元素及屬性

目錄 1 引言 2 智能表單控件-type 3 表單屬性 form input 5 答疑--解決required自定義提示信息 1 引言 HTML5引入了一系列新的表單輸入類型&#xff0c;如email、url、number、range、date、time、datetime-local、month、week、search、color和tel等。這些新類型增強了表…
閱讀更多...
FFmpeg源碼：bytestream_get_byte函數解析

FFmpeg源碼：bytestream_get_byte函數解析

一、引言 FFmpeg源碼中經常使用到bytestream_get_byte這個函數&#xff0c;比如使用FFmpeg對BMP圖片進行解析&#xff0c;其源碼會調用函數bmp_decode_frame&#xff0c;而該函數內部會通過bytestream_get_byte讀取BMP 的header。本文講解函數bytestream_get_byte的作用和內部…
閱讀更多...
Spark SQL 中DataFrame DSL的使用

Spark SQL 中DataFrame DSL的使用

在上一篇文章中已經大致說明了DataFrame APi,下面我們具體介紹DataFrame DSL的使用。DataFrame DSL是一種命令式編寫Spark SQL的方式&#xff0c;使用的是一種類sql的風格語法。 文章鏈接&#xff1a; 一、單詞統計案例引入 import org.apache.spark.sql.{DataFrame, SaveMod…
閱讀更多...
最新文章

Copyright @ 2022~2023