大家好！我是曾續緣🧡

今天是《LeetCode 熱題 100》系列

發車第 64 天

二分查找第 2 題

??點贊 👍 收藏 ?再看，養成習慣

搜索二維矩陣

給你一個滿足下述兩條屬性的 m x n 整數矩陣：

• 每行中的整數從左到右按非嚴格遞增順序排列。
• 每行的第一個整數大于前一行的最后一個整數。

給你一個整數 target ，如果 target 在矩陣中，返回 true ；否則，返回 false 。

示例 1：

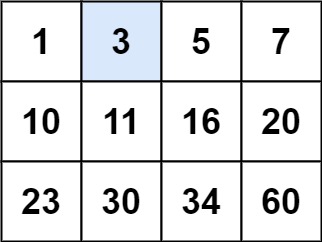輸入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
輸出：true

示例 2：

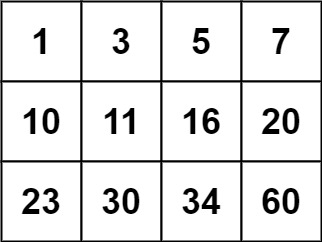輸入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
輸出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

難度：💖💖

解題方法

首先，我們需要明確題目中矩陣的兩個特性：每一行從左到右遞增，每一行的第一個數比上一行的最后一個數大。這意味著整個矩陣在某種意義上是“排序”的，我們可以利用這一點來快速定位元素。
在解決這個問題時，我們可以把矩陣看作一個一維數組，然后使用二分查找算法。如何把二維矩陣映射到一維數組呢？考慮到矩陣有 m 行 n 列，我們可以將矩陣的行優先展開，即先放置第一行的所有元素，然后是第二行，依此類推。這樣，矩陣中的元素 matrix[i][j] 將會映射到一維數組中的位置 i * n + j。
接下來，我們可以在這個假想的一維數組上使用二分查找。二分查找的基本思想是在有序數組中通過重復將搜索區間減半來定位目標值。具體步驟如下：

1. 確定搜索范圍的最小和最大索引，初始時最小索引 l 為 0，最大索引 r 為 m * n - 1（即矩陣中最后一個元素的索引）。
2. 計算中間索引 mid = (l + r) / 2，然后找到這個索引對應的矩陣中的元素 matrix[mid / n][mid % n]。
3. 比較這個元素與目標值 target：
   • 如果相等，說明找到了目標值，返回 true。
   • 如果小于目標值，說明目標值應該位于當前元素的右側，于是我們將搜索范圍的最小索引調整為 mid + 1。
   • 如果大于目標值，說明目標值應該位于當前元素的左側，于是我們將搜索范圍的最大索引調整為 mid - 1。
4. 重復步驟 2 和 3，直到找到目標值或者搜索范圍為空（即 l > r），此時如果還沒有找到目標值，則返回 false。
   這個方法的時間復雜度是 O(log(m*n))，空間復雜度是 O(1)，因為我們在原地進行搜索，沒有使用額外的空間。

Code

class Solution {public boolean searchMatrix(int[][] matrix, int target) {int m = matrix.length, n = matrix[0].length;int l = 0, r = m * n - 1;while(l <= r){int mid = (l + r) / 2;int val = matrix[mid / n][mid % n];if(val == target){return true;}else if(val < target){l = mid + 1;}else{r = mid - 1;}}return false;}
}