https://www.bilibili.com/video/BV1fG4y1y7Eq/?spm_id_from=333.788&vd_source=e3f5663396069f720fed59c6d41ed6f7

一、什么是雷達成像

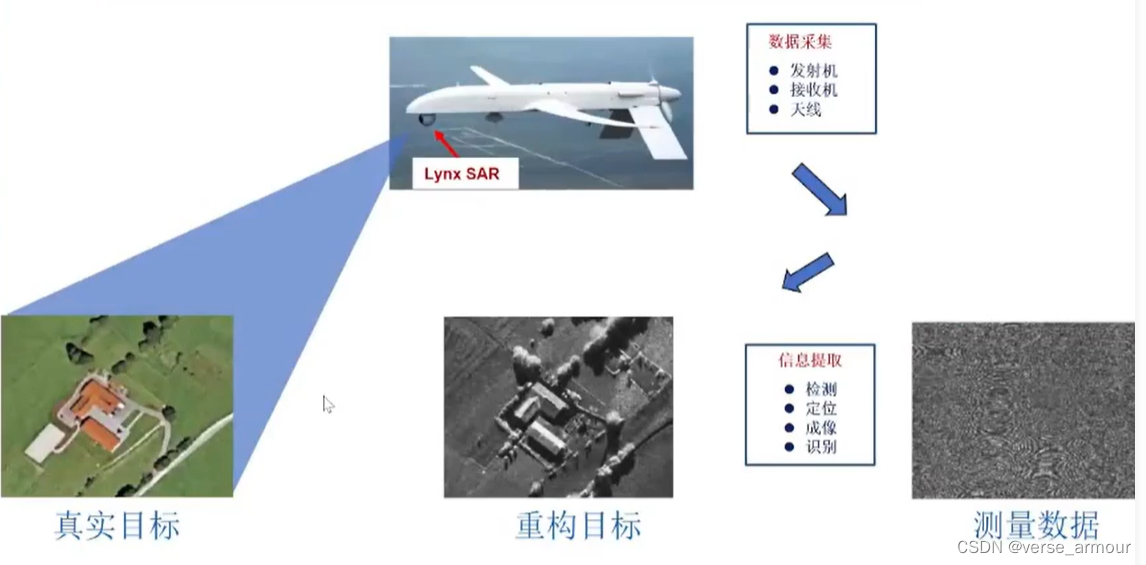
成像雷達是一種主動傳感器，它利用電磁波作為媒介，采集目標回撥數據，并從回波數據中提取目標空間集合形狀信息（重構目標圖像）

（1）主要的遙感探測手段：光學、紅外和雷達

雷達成像相比于光學成像、紅外成像的優勢：

• 全天候工作（不受氣候條件限制）
• 全天時工作（不受白天黑夜限制）
• 探測距離遠（幾百公里甚至幾千公里）
• 是光學、紅外的補充（不同頻譜觀察）

（2）從數學的角度：雷達成像主要研究什么？

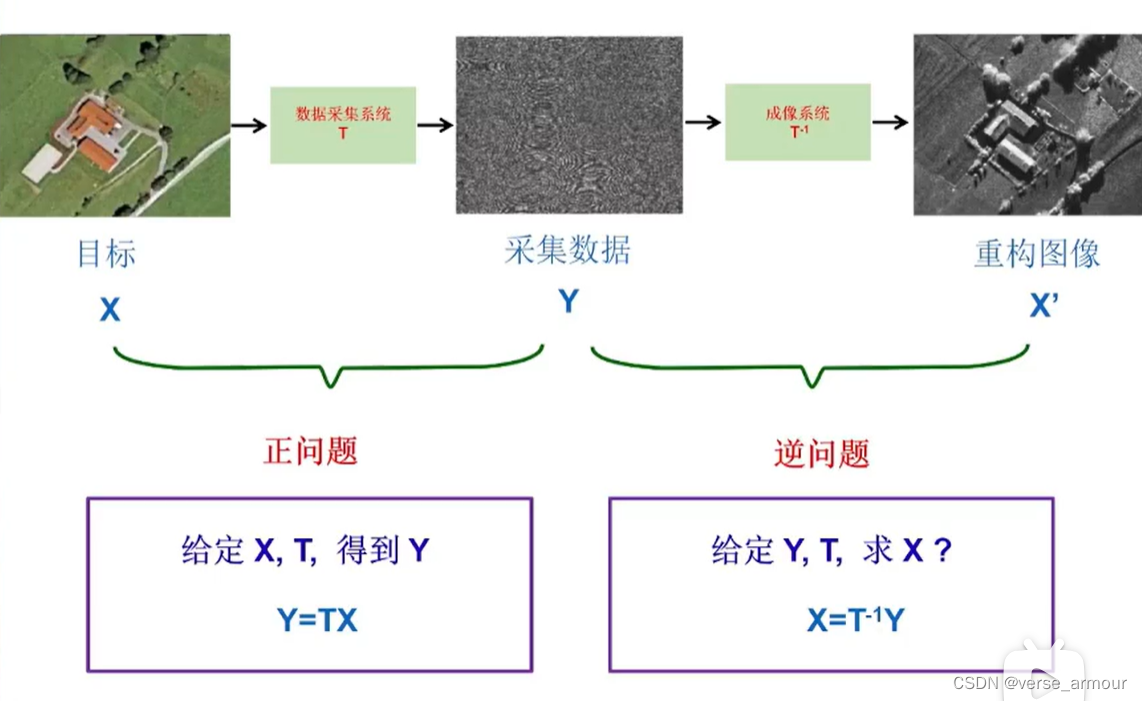
雷達成像研究的兩個問題：正問題和逆問題

• 正問題：從被觀測目標$X$經過數據采集系統$T$得到采集數據$Y$。即給定$X$,$T$,求解$Y$。$Y=TX$。
• 逆問題：從采集數據$Y$經過成像系統$T^{?1}$得到重構圖像$X^{{}^{\prime }}$。即給定$Y$,$T$,求解$X$。$X=T^{?1}Y$。

雷達設計的兩大任務：數據采集和信息提取

數據采集：$y=Tx+n$

算子$T$由雷達的發射信號決定的，包括發射信號的波形 、極化方式、天線、發射信號調制。

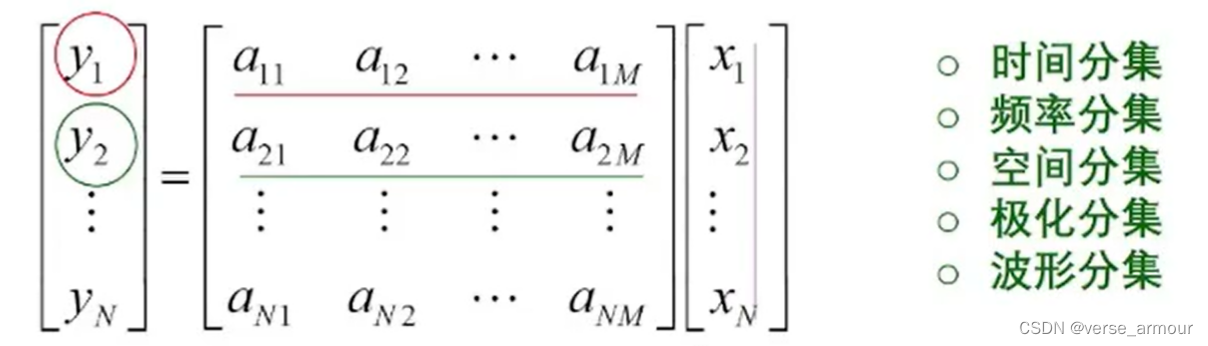
如何設計雷達的發射信號$T$使得可以更好地提取信息$x$？
（1）矩陣$T$要滿足每一行都不一樣，因為有多少個未知數，就得有多少個方程，這樣才能把未知向量$x$解出來。
（2）最好的情況是矩陣$T$是正交的，這樣這個矩陣就沒有冗余。
（3）放在雷達成像的背景下來理解：就是要設計的這個數據采集系統（觀測方式）最好要使得我們每次的觀測都不一樣，這樣才能最大化地獲取這個目標的信息。最大化獲取目標的信息才能方便重構目標圖像，提高重構圖像的精度。

信息提取：$y?>x?$

通常工程上對這個方程的求解認為是一個變態的問題。

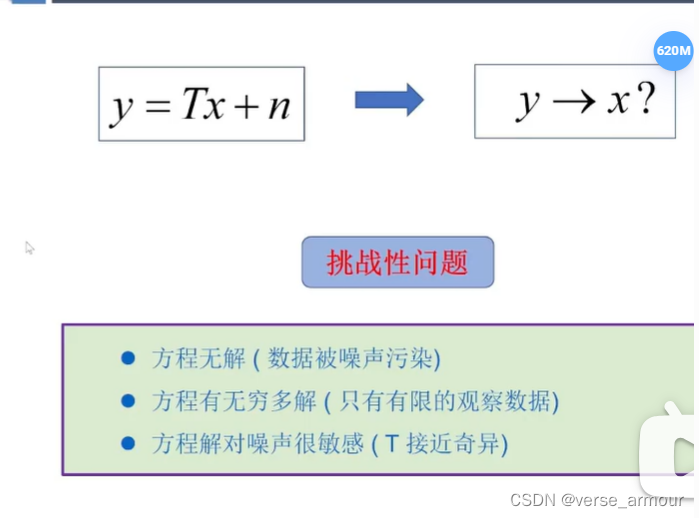
三個挑戰性問題：
（1）方程無解（數據被噪聲污染）
（2）方程有無窮多解（只有有限的觀察數據）
任何一個觀測目標都可以認為是一個無窮維度的向量，但是我們實際觀察到的數據是有限維度的，即我們獲得的方程的個數小于實際觀測目標的維度（方程的個數少于未知數的個數），則該方程組有無窮多個解。
（3）方程解對噪聲很敏感（$T$接近奇異，行列式非常趨近于0）
此時，方程組有唯一解，但是這個解對噪聲非常敏感。只要$T$有一點噪聲的擾動，這個解$x$就會偏離真實值很大。
工程上對于無解的情況可以求出一個最小二乘解；無窮多個解的時候可以求出一個最小范數。比如我們去成像一個飛機，我們不需要得到一個顯微鏡級別的成像，我們只需要達到米級或者亞米級就夠了，沒有必要達到分子級或者原子級的精度，得到一個精確解。因此，在工程上，沒有必要求出這個精確解。

二、SAR的多維理解

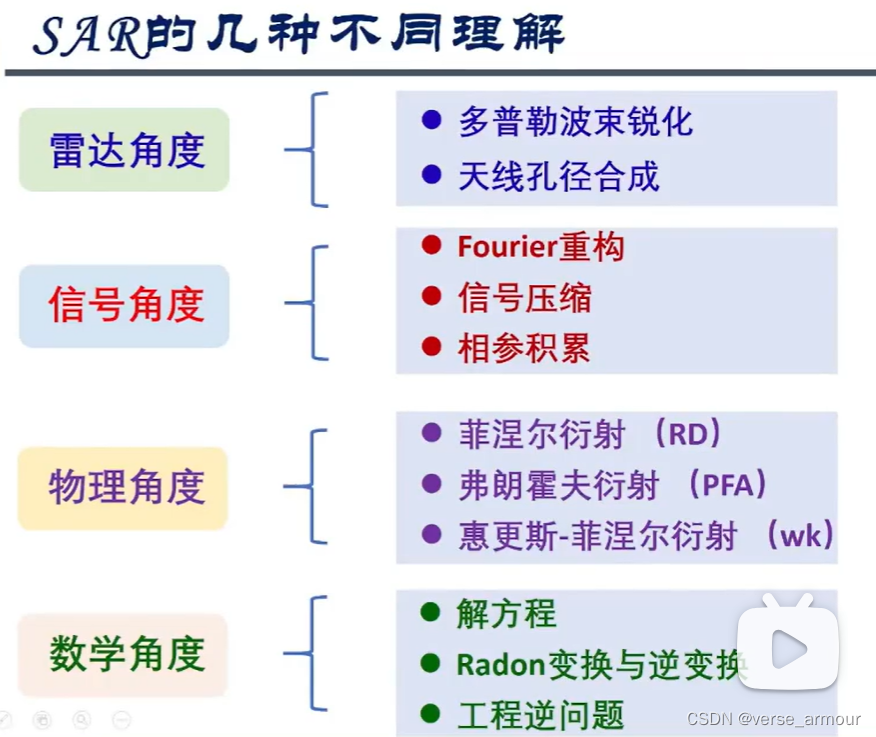
（1）雷達角度理解SAR

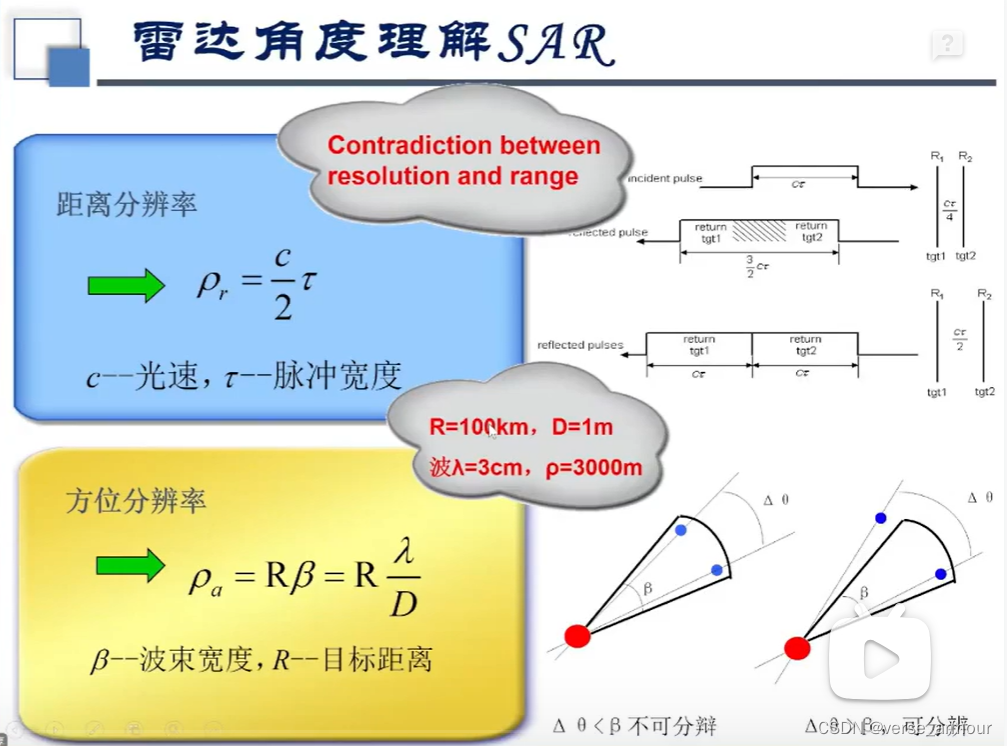
$D$表示天線的長度。如果想要方位分辨率達到1m，但是$R=100km，\lambda =3cm$保持不變，$D=3000m$。
實現困難：

• 3000m甚至30000m的天線孔徑在物理上很難實現
• 即使實現了也很難在飛機、導彈、衛星上應用
  
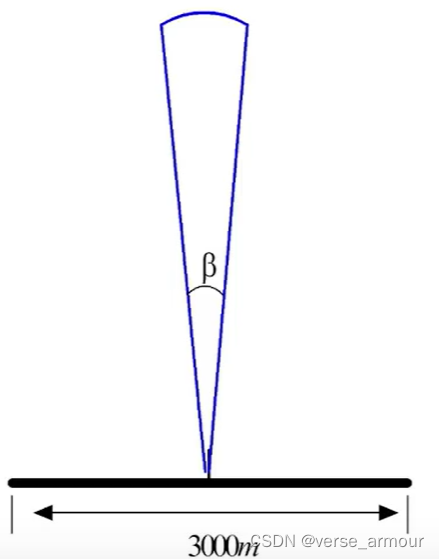
  SAR是如何解決這個問題的呢？
  
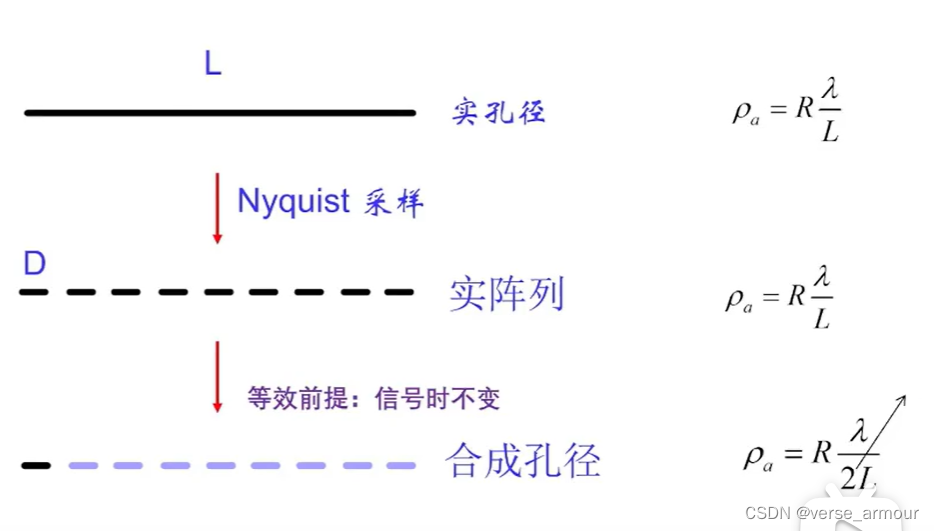
• 在空間中將天線孔徑通過Nyquist采樣離散化。
• 實陣列：得到的實陣列仍然不方便應用在飛機、導彈、衛星上，實陣列相當于在多個不同的角度觀察，模擬了一個大的天線孔徑的觀察效果。（實孔徑是一次就可以從不同角度去觀察）
• 合成孔徑：僅用實陣列中的一個小的天線孔徑，去達到一系列實陣列的觀察效果：用時間換空間。用一個天線孔徑從不同的位置去觀察。
  等效前提：信號時不變。SAR成像關注的是地面目標，一般情況下地面目標在不同時間內的散射特性可以認為保持不變，滿足信號時不變的前提。

（2）信號處理角度理解SAR

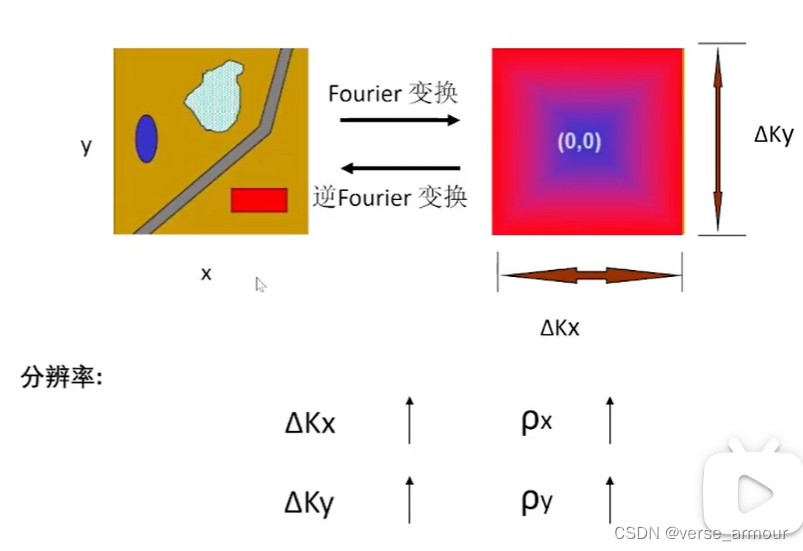
任何空域有限的信號，在頻譜上是無限的。但是我們觀察到的頻譜又一定是有限的，通過有限的頻譜作傅里葉逆變換很難重構出一個高精度的目標。

實際上我們去獲取頻譜的時候只能獲取一些離散的采樣值，可以是矩形格式采樣，也可以是極坐標格式采樣。

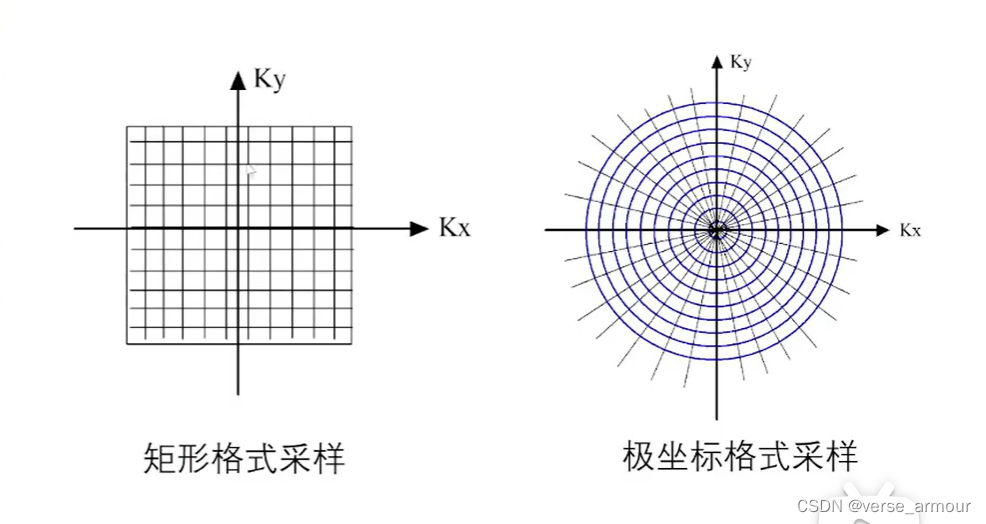
對于SAR成像采集到的信號，經過一定的預處理之后，得到的就是極坐標格式的采樣。在極徑上采樣一定的范圍，在極角上采樣一定的范圍。
在極徑上采樣的位置由載頻決定，載頻越高，在極徑上的范圍就越往外移；
在極徑上采樣的長度由發射帶寬決定，發射信號的帶寬越寬，在極徑上采樣的寬度就越寬；
在極角上采樣的范圍由雷達觀測目標時的轉角決定，轉角越大，在頻域上的采集的極角角度就越大。

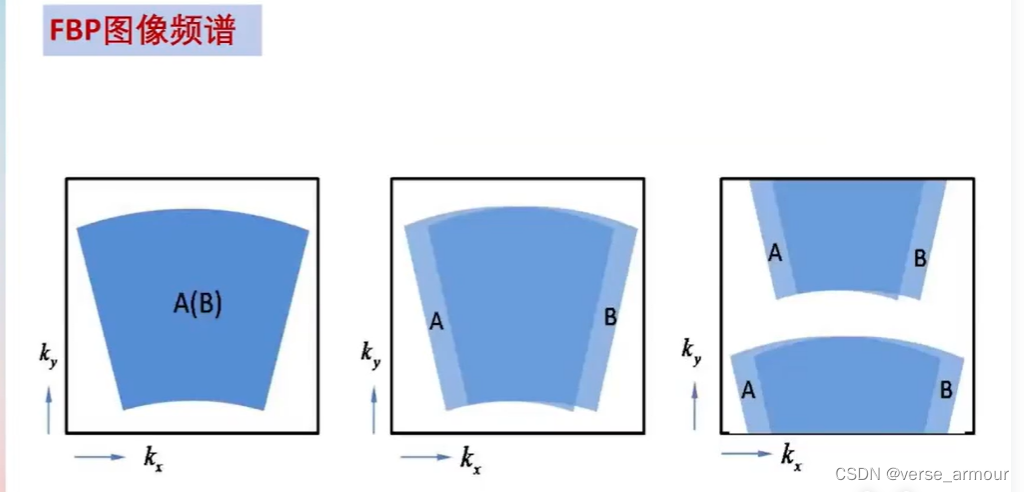
聚焦上圖，我們可以知道右圖的載頻大于左邊的載頻。在同樣的極角下，范圍更大，即方位分辨率更高。

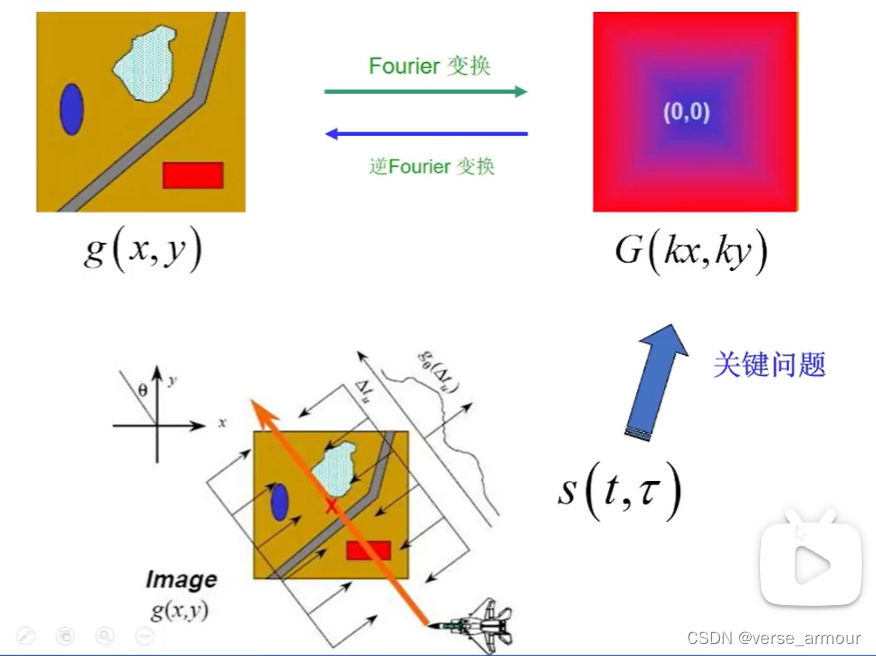
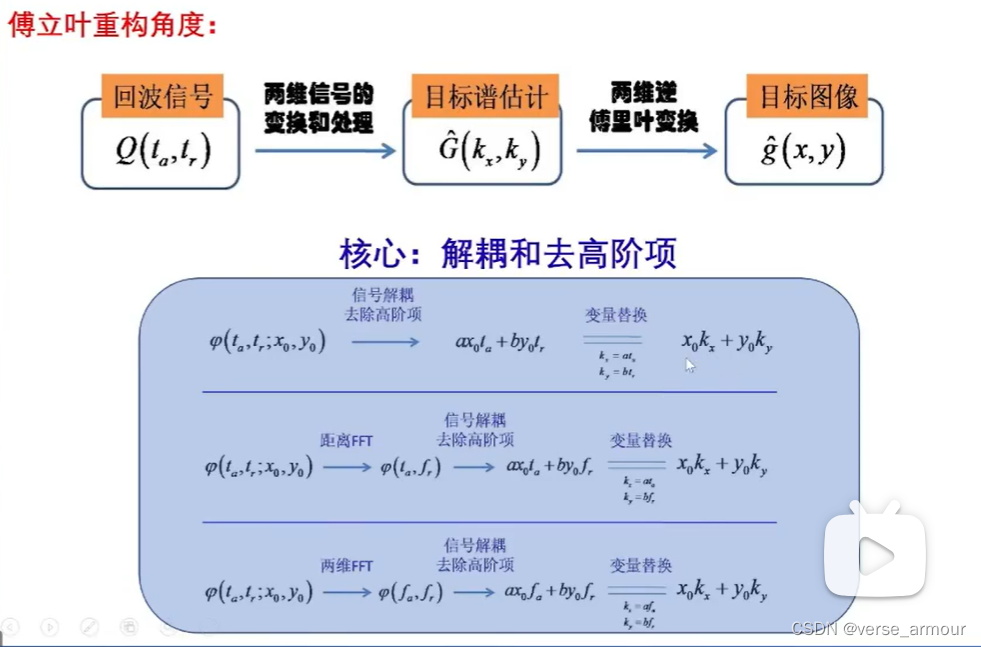
為什么可以從回波信號變換到兩維頻譜？為什么說回波信號就反映了頻譜？——數學原理

這是因為，雷達的回波信號是發射信號和目標函數二維投影的卷積，即回波信號既包含發射信號的信息，也包含了投影的信息。但是發射信號只是一個工具，我們會從回波信號中將發現信號去掉，留下來的就是目標二維函數的一維投影的信息。將一維投影做一個傅里葉變換就可以得到兩維頻譜的切片。

單個脈沖只能得到一個角度的切片：

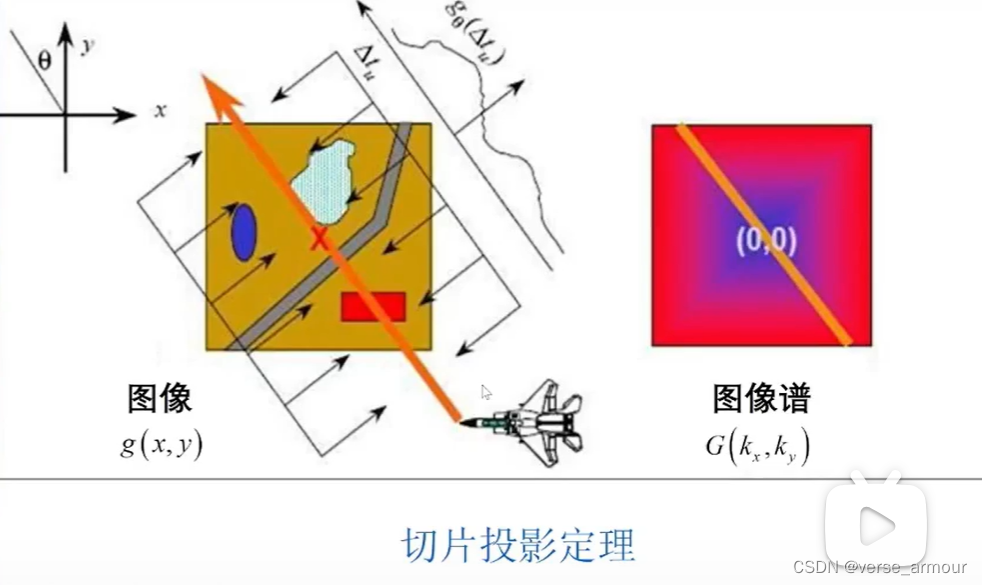
我們讓雷達發射多個脈沖，可以得到不同角度的頻譜切片。當我們得到足夠多的切片時，我們就能得到一個較為完整的頻譜。

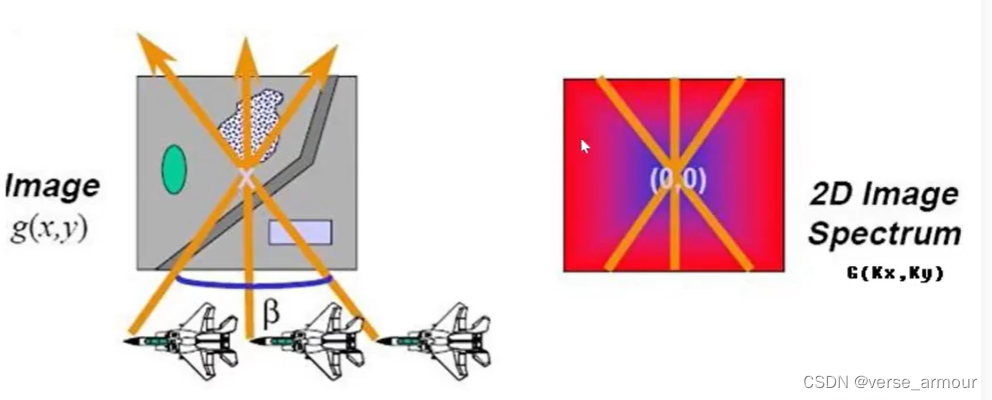
具體的算法實現可能會不一樣。

（3）數學角度理解SAR

離散情況

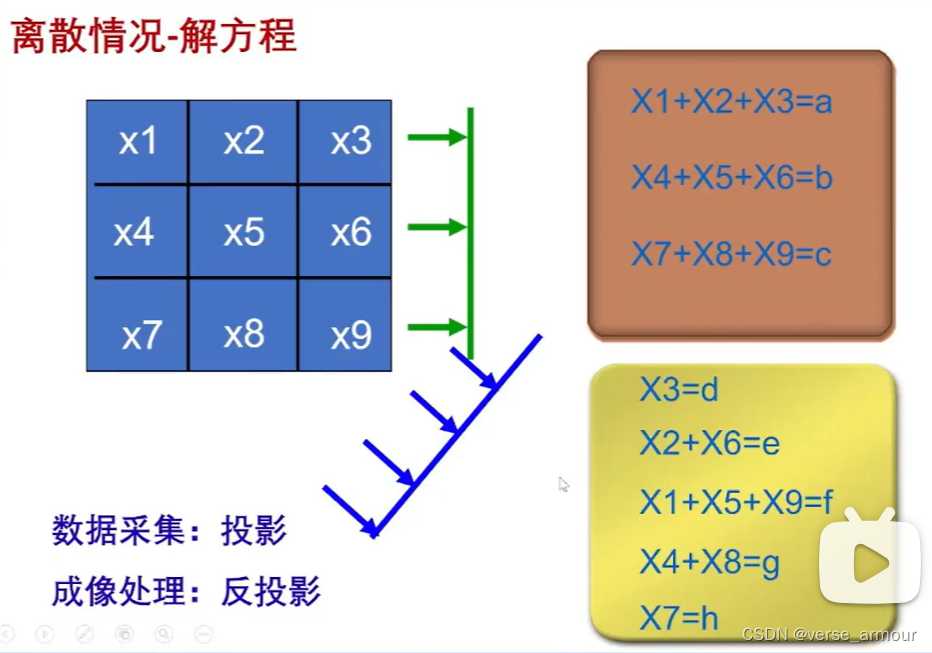
• 數據采集的過程就是投影值測量的過程
• 重構圖像的過程就是解不同角度列的投影值方程組成的方程組過程（這只是數學角度的一個理解，真正工程上去實現的時候，方程組的維度特別大，所以不會有人真的去解這個方程組）

離散情況重構圖像：反投影算法

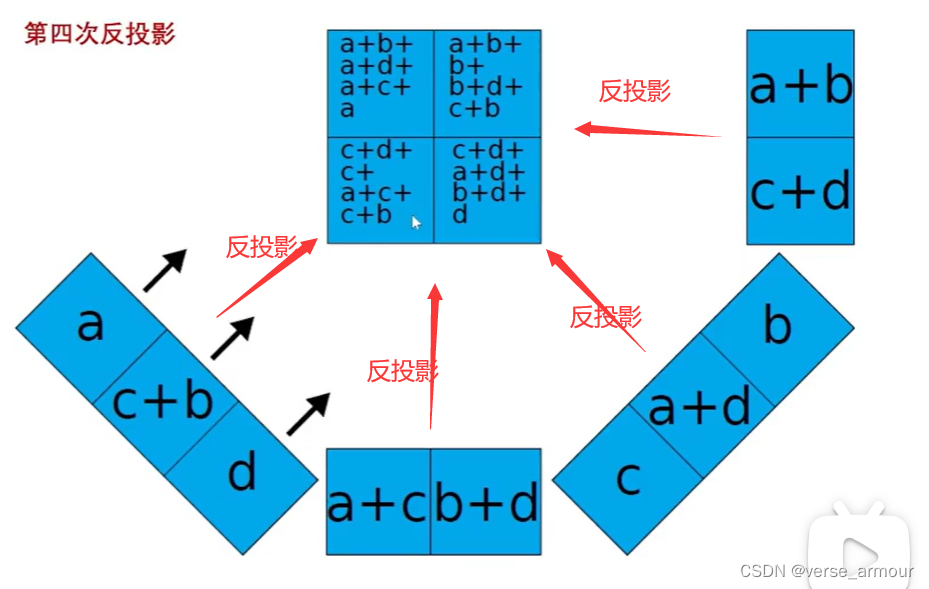
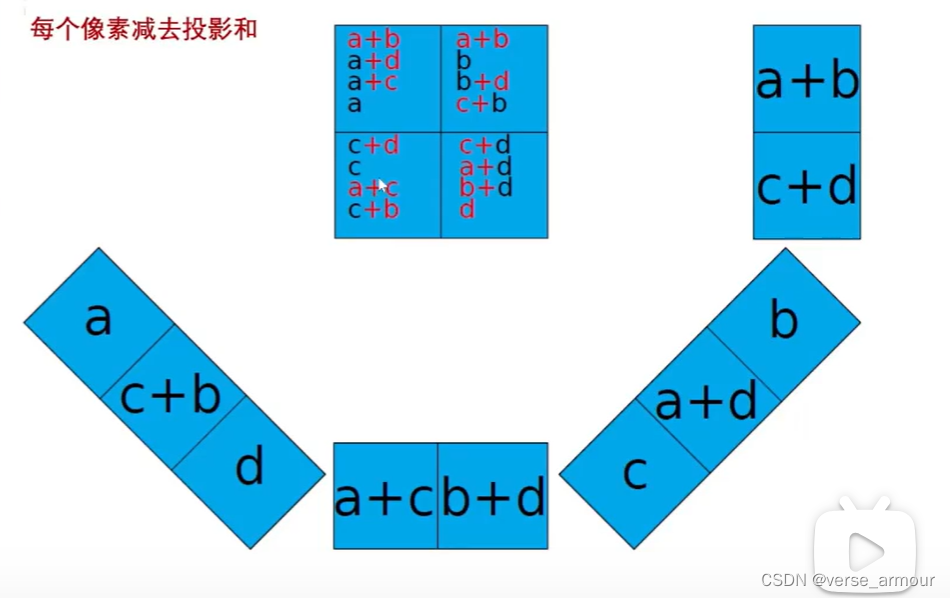
在SAR成像中，加完了就相當于抵消掉了。去掉之后剩下，3a,3b,3c,3d，和原來的就相差一個比例系數。

連續情況

連續情況重構圖像：Randon變換和反變換

• 數據采集：Radon變換的過程
• 圖像重構：Radon反變換的過程
  
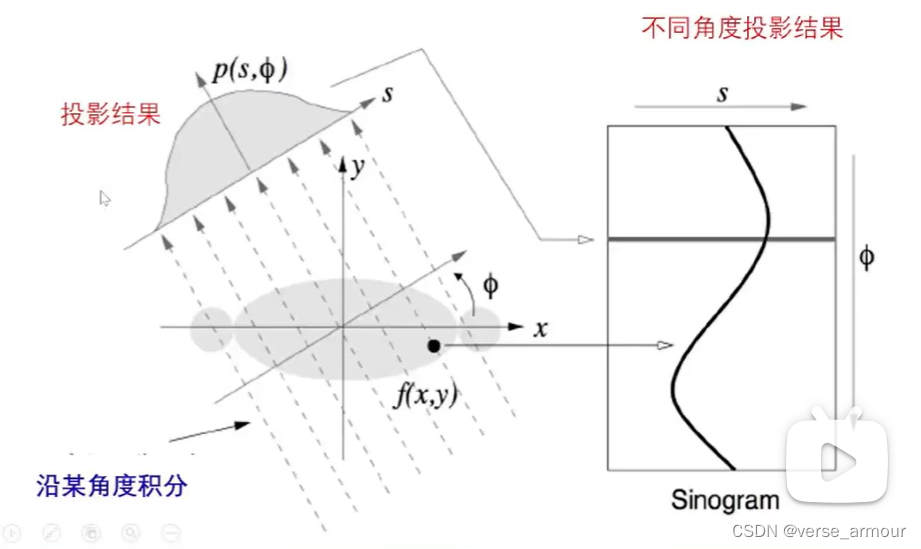
  在傳統的Radon變換中，通常是沿著一條直線去投影；但是在SAR成像中，一般是沿著一條弧形去投影。
  
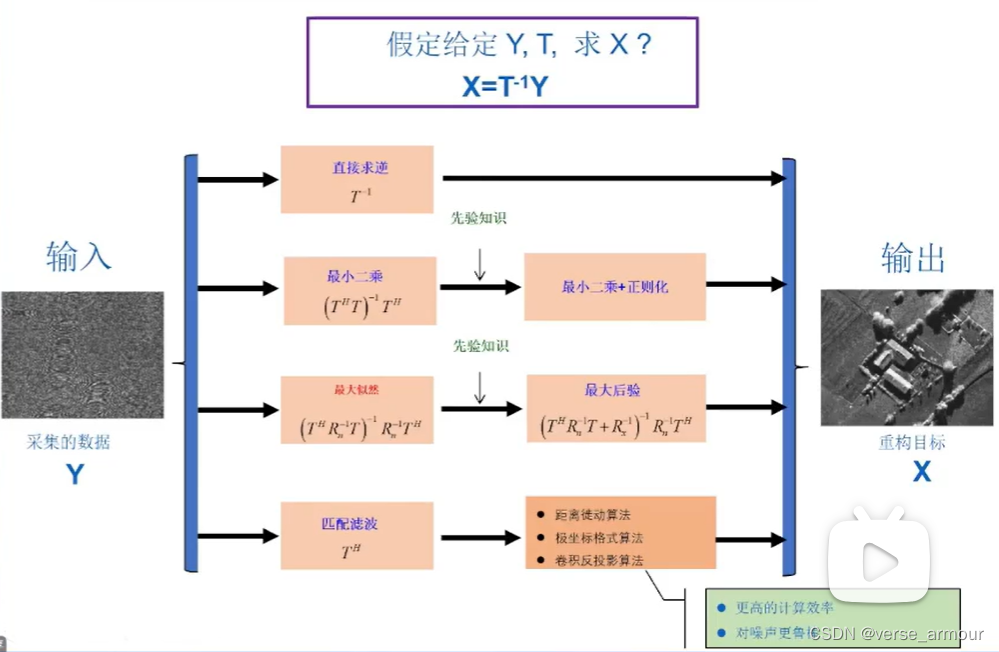
  工程上一般會避免矩陣求逆（計算量大，魯棒性差）來求$X$，一般會用匹配濾波來實現。但這一定程度上犧牲了圖像重構的精度。

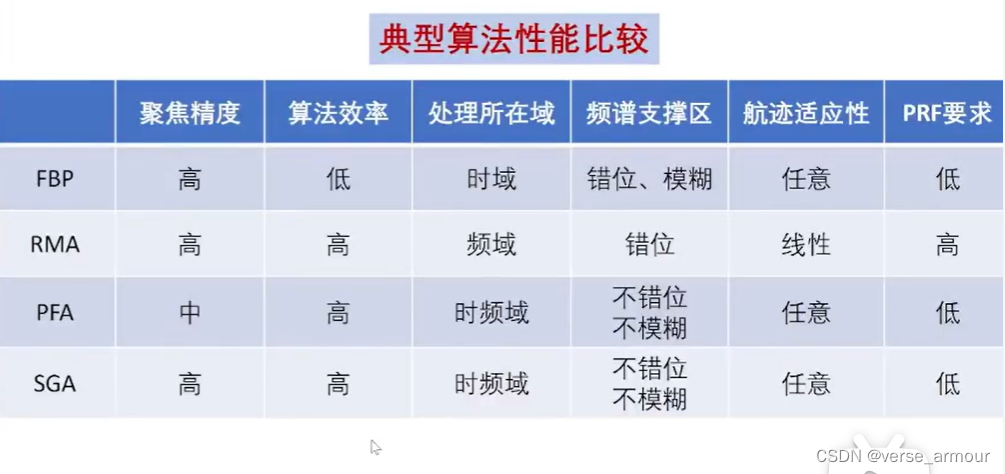
三、SAR成像算法的統一解釋

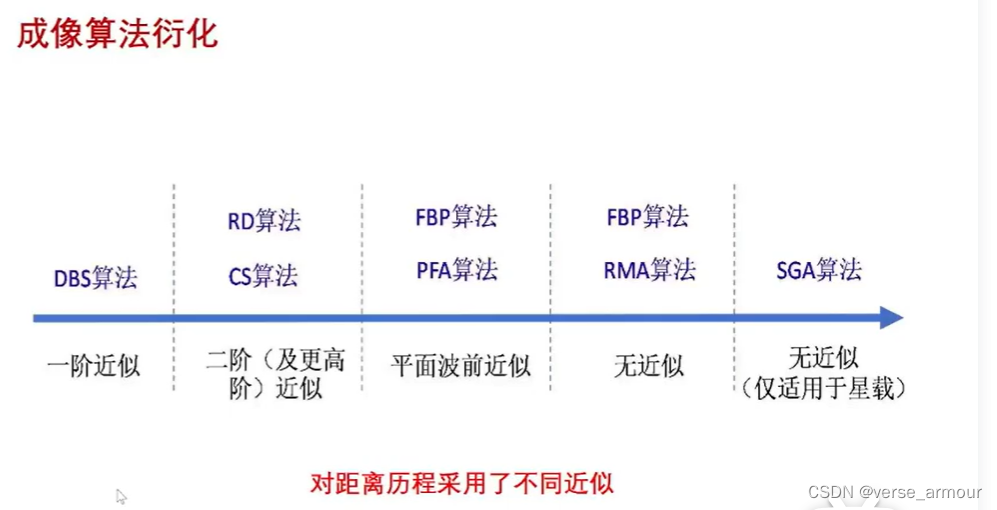
這些算法的本質都是匹配濾波，不同點在于對距離歷程采用了不同近似

適用于星載的SGA算法比較好地解決了軌道彎曲、軌道非共面等問題，沒有對任何距離歷程采取近似。

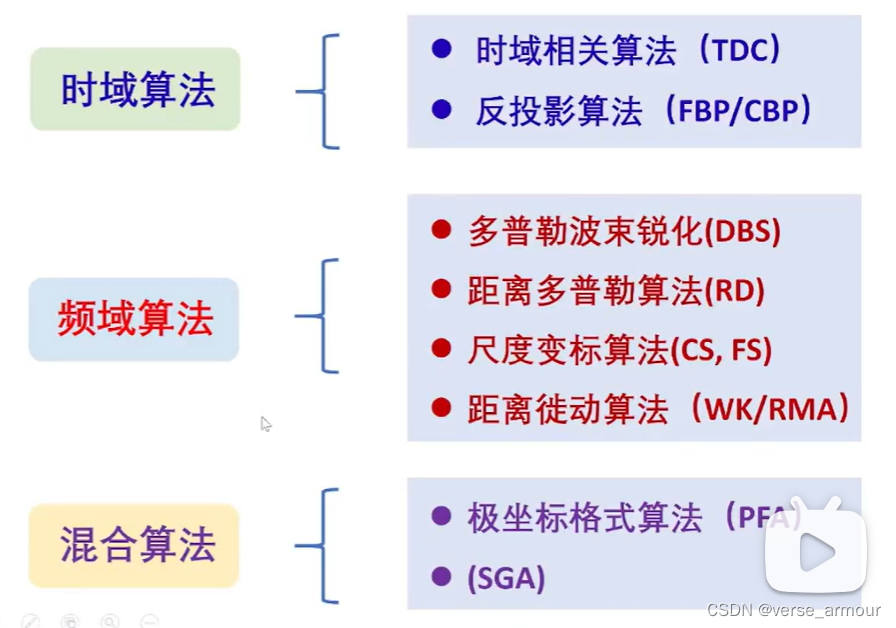
（1）極坐標格式算法

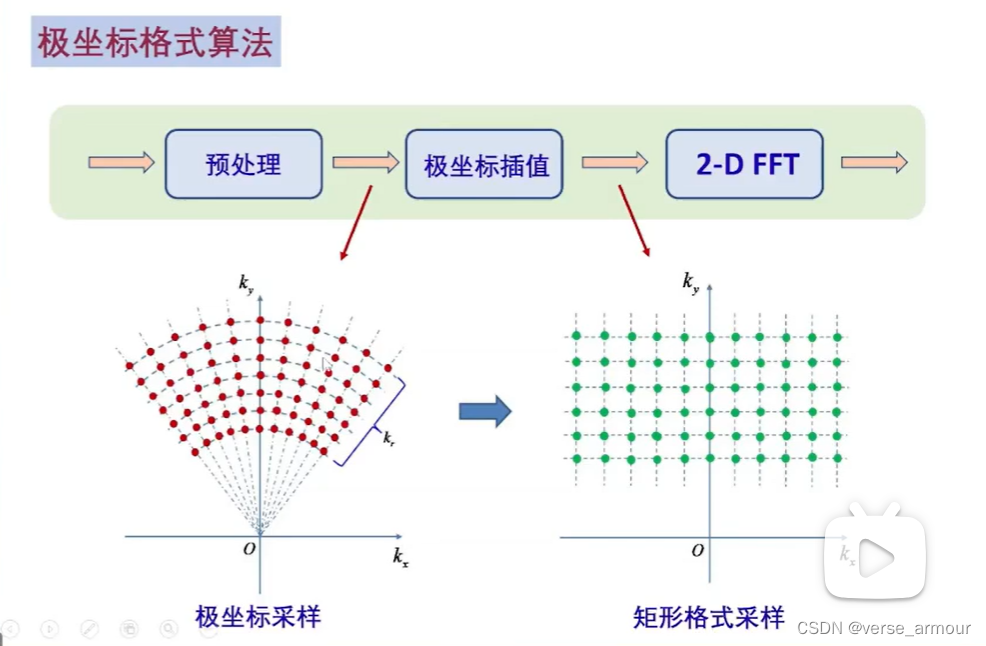
將極坐標采樣通過一個重采樣得到矩形格式采樣，這樣方便使用2-D FFT來進行圖像重構。

極坐標格式轉換

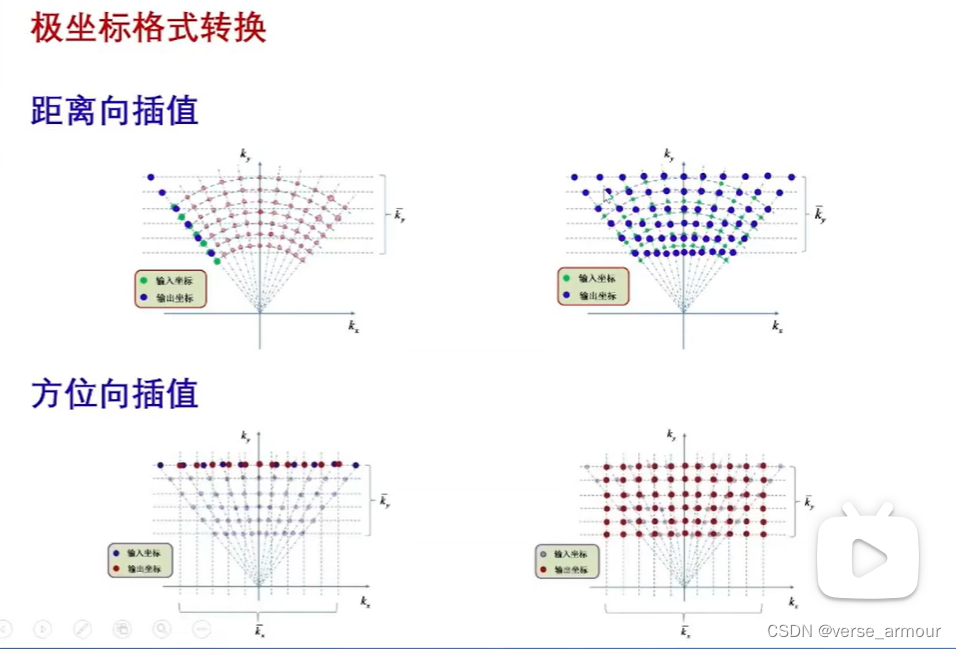
（2）距離徙動算法

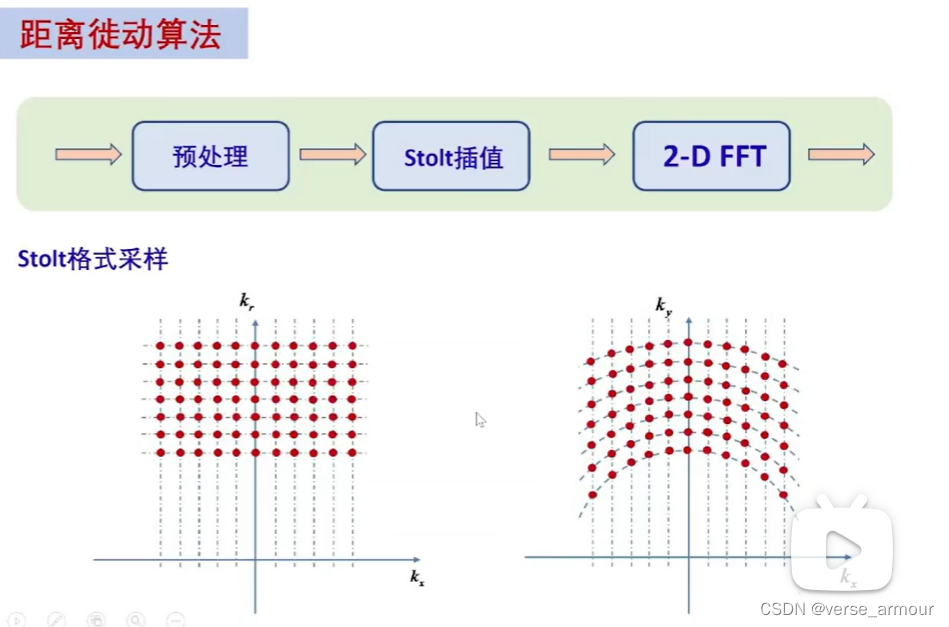
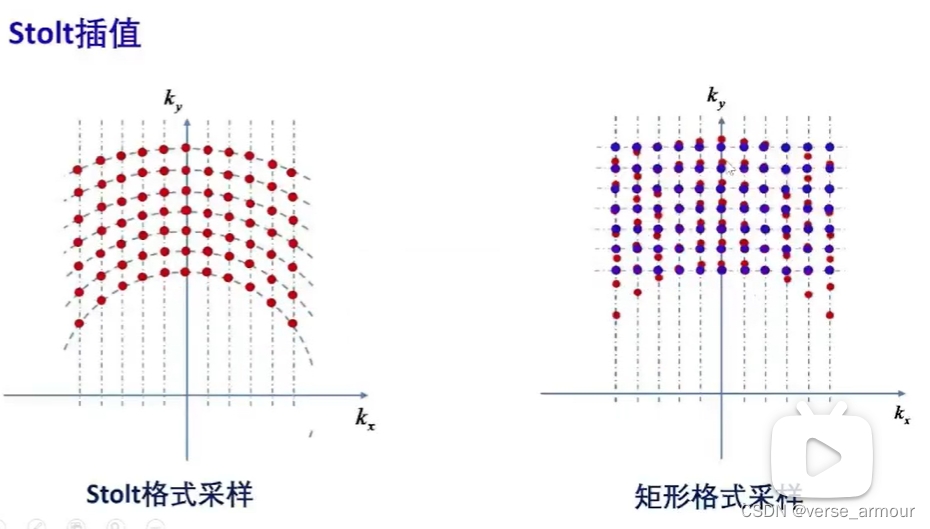
（3）卷積反投影算法

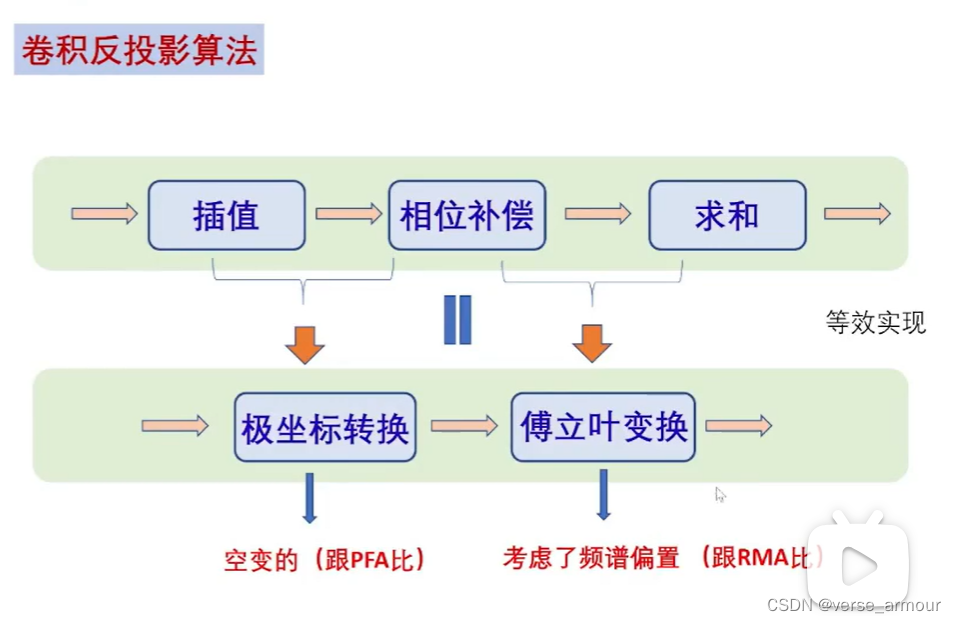
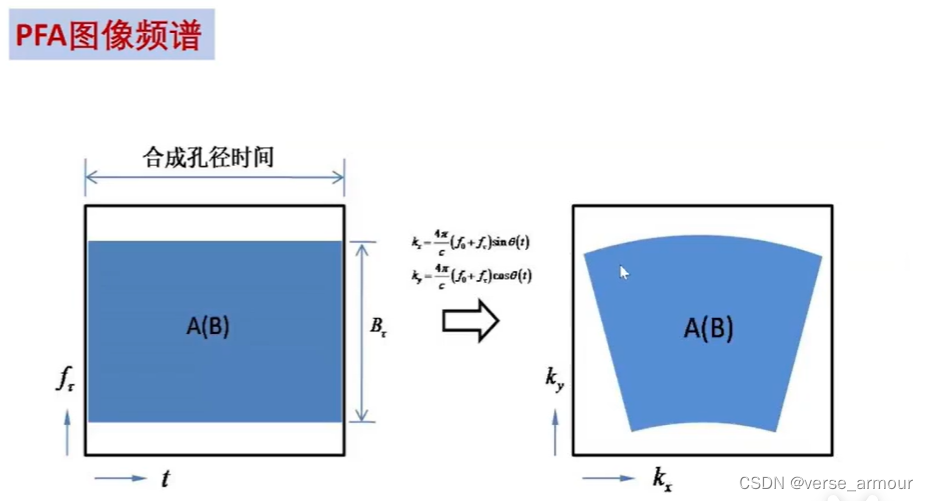
PFA算法認為對于場景中不同點的頻譜都是一樣的。但其實這是不準確的，空間中每個點的兩維頻譜是不一樣的，這也便于理解為什么極坐標格式算法（PFA）是近似的。

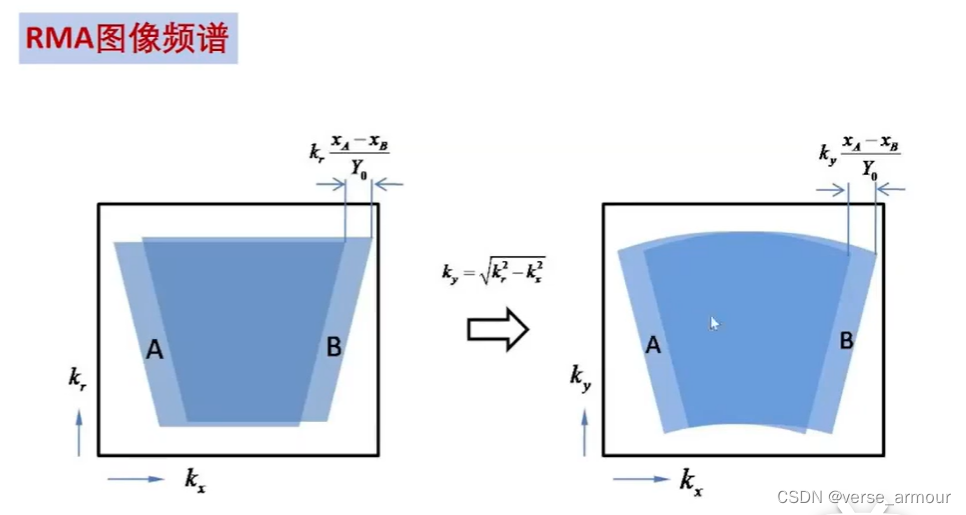
主要考慮了方位不同的點，頻譜會在方位上有一個錯位。