系列文章目錄

?第一篇：【排序算法】①直接插入排序-CSDN博客

第二篇：【排序算法】②希爾排序-CSDN博客

第三篇：【排序算法】③直接選擇排序-CSDN博客

第四篇：【排序算法】④堆排序-CSDN博客

第五篇：【排序算法】⑤冒泡排序-CSDN博客

第六篇：【排序算法】⑥快速排序：Hoare、挖坑法、前后指針法-CSDN博客

第七篇：【排序算法】⑦歸并排序-CSDN博客

---

目錄

系列文章目錄

前言

一、希爾排序是什么？

算法思想

二、為什么希爾排序能做到排序？

三、實現希爾排序

四、分析希爾排序

總結

---

---

前言

所謂排序，就是使一串記錄，按照其中的某個或某些關鍵字的大小，遞增或遞減的排列起來的操作。

為什么我們要學習排序？筆者認為有兩點理由：一是面對浩如煙海的各種數據，我們應該學習如何分類、控制這些數據，而排序自然是少不了的；二是人類社會從古至今一直在“排序”，人與人之間，物與物之間，排序涉及到社會的方方面面。

學習并理解排序，不僅有助于工作學習，或許對一些其他方面的理解也會起動到推的效果。

---

一、希爾排序是什么？

希爾排序法又稱縮小增量法，是在直接插入排序的基礎上進行優化得來的排序算法。

算法思想

希爾排序法的基本思想是：先選定一個間距整數gap，把待排序文件中所有記錄分成gap個組，所有距離為gap的記錄分在同一組內，并對每一組內的記錄進行直接插入排序。然后，gap--，重復上述分組和排序的工作。當到達gap=1時，所有記錄在統一組內排好序。

簡單來說，希爾排序分為“預排序”和“正式排序”兩步。

---

二、為什么希爾排序能做到排序？

這里筆者畫了草圖以幫助大家理解希爾排序：

假設我們排升序，數組為{7 ，1 ，3 ，9 ，6 ，5 ，4 ，8 ，2 ，0}

假設設gap=3：

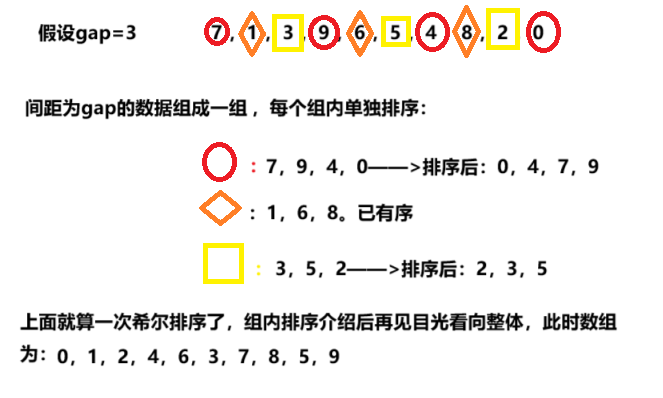
此時將gap-1，在再上一次排序的基礎上排：

gap=2，數組為{0，1，2，4，6，3，7，8，5，9}

再將gap-1，此時gap==1，實質上成為直接插入排序。

為什么要分幾次預排序，然后還要調用直接插入排序？

還記得插入排序什么時候效率最高嗎，當數組接近有序的時候！預排序的過程其實就是讓數組接近有序，為后面的gap=1時的插入排序做準備，也就是說希爾排序的最后一步必須是gap==1時的直接插入排序！

三、實現希爾排序

void ShellSort(int* a, int n)
{if (!a)return;int gap = n;//gap>1:確保最后一趟gap==1while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - 1; i += gap){int end = i;int temp = a[end + gap];while (end >= 0&&end+gap<n){//if (temp > a[end])遞減if(temp < a[end])//遞增{a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = temp;}}
}

代碼講解：

①gap=gap/3，通過將gap/3快速將整個區間劃分為多個小區間進行預處理操作。這里除以3是基于前人所做的大量總結中得出的最優解：在效率和計算復雜度間取得平衡。

若gap/2，則遞減過慢且中間需要較多次的預排序過程；若gap/>3的數，則遞減過快，難以達成預排序的目的：讓數組變得盡量有序。

②gap=gap/3+1，這個+1的目的是確保gap永不小于 1，并且使得最后一次循環必定執行gap==1時的直接插入排序。

③for循環中實質為直接插入排序，在上一篇中已經介紹過，若讀者有疑惑的地方歡迎在評論區討論。

---

四、分析希爾排序

1. 希爾排序是對直接插入排序的優化。

2. 當gap > 1時都是預排序，目的是讓數組更接近于有序。當gap == 1時，數組已經接近有序的了，這樣就會很快。這樣整體而言，可以達到優化的效果。

3.時間復雜度：希爾排序的時間復雜度較難計算，需要用到數學中的概率論證明，這里就省略證明過程，希爾排序的時間復雜度隨gap的變化而變化，上述代碼中的gap=gap/3+1的時間復雜度為O(N^1.3);

4.空間復雜度為O(1);

5.穩定性分析：不穩定！希爾排序的不穩定性源于它在排序過程中會進行長距離的元素交換，這可能導致相同值的元素在排序后改變相對順序。

比如：數組{5A, 2, 1 ,?5B, 3}（5A和5B是值相同但需區分順序的兩個元素），希爾排序最后結果為{1，2，3，5B，5A}，排序前5A在5B前，排序后5A在5B后！

---

總結

本文是【排序算法】系類第二篇，主要介紹了什么希爾排序，以及如何實現希爾排序，最后分析了希爾排序的特性。

希望對你有所幫助。

閱完點贊，手留余香~