什么是神經網絡
人工神經網絡( Artificial Neural Network, 簡寫為ANN)也簡稱為神經網絡(NN),是一種模仿生物神經網絡結構和功能的計算模型,人腦可以看做是一個生物神經網絡,由眾多的神經元連接而成.各個神經元傳遞復雜的電信號,樹突接收到輸入信號,然后對信號進行處理,通過軸突輸出信號.

當電信號通過樹突進入到細胞核時,會逐漸聚集電荷。達到一定的電位后,細胞就會被激活,通過軸突發出電信號。
構建人工神經網絡
神經網絡由多個神經元組成,構建神經網絡就是構建神經元.基礎神經元如下

?這個過程就像,來源不同樹突(樹突都會有不同的權重)的信息, 進行的加權計算, 輸入到細胞中做加和,再通過激活函數輸出細胞值。
然后使用多個神經元構成神經網絡,相鄰層的神經元互相連接

????????神經網絡中信息只向一個方向移動,即從輸入節點向前移動,通過隱藏節點,再向輸出節點移動。其中的基本部分是:
- ?輸入層(Input Layer): 即輸入x的那一層(如圖像、文本、聲音等)。每個輸入特征對應一個神經元。輸入層將數據傳遞給下一層的神經元。
- ?輸出層(Output Layer): 即輸出y的那一層。輸出層的神經元根據網絡的任務(回歸、分類等)生成最終的預測結果。
- ?隱藏層(Hidden Layers): 輸入層和輸出層之間都是隱藏層,神經網絡的“深度”通常由隱藏層的數量決定。
????????隱藏層的神經元通過加權和激活函數處理輸入,并將結果傳遞到下一層。?特點是:
- 同一層的神經元之間沒有連接
- 第 N 層的每個神經元和第 N-1層 的所有神經元相連(這就是full connected的含義),這就是全連接神經網絡
- 全連接神經網絡接收的樣本數據是二維的,數據在每一層之間需要以二維的形式傳遞
- 第N-1層神經元的輸出就是第N層神經元的輸入 每個連接都有一個權重值(w系數和b系數)
神經網絡內部狀態值和激活值

?內部狀態值是是神經元對輸入信號的加權求和結果,加上偏置項后的線性組合。
????????wi為內部狀態值梯度(權重矩陣與偏置可以初始化)

激活值(通常記為?a)是內部狀態值通過激活函數?f(?)?非線性變換后的輸出,如sigmoid,tanh,relu,softmax即

????????總的來說,神經網絡是一種模仿生物神經網絡結構和功能的計算模型,由輸入層,輸出層,和隱藏層構成,每一層都由神經元構成.
????????神經元包含內部狀態值梯度w,偏置值b,激活函數f(x),通過對外部輸入進行加權計算得到內部狀態值z,將z輸入激活函數進行非線性變換得到激活值傳給下一個神經元或者輸出.
激活函數
????????激活函數用于對每層的輸出數據進行變換,進而為整個網絡注入了非線性因素.此時,神經網絡就可以你和各種曲線.
- 如果沒有引入非線性因素,神經網絡等價于一個線性模型
- 通過給網絡輸出增加激活函數, 實現引入非線性因素, 使得網絡模型可以逼近任意函數, 提升網絡對復雜問題的擬合能力.
如果不使用激活函數,整個網絡雖然看起來復雜,其本質還相當于一種線性模型,如下公式所示:
?
常見激活函數及特點?

激活函數作用:向神經網絡中添加非線性因素
激活函數選擇方法:relu能且僅能用于隱藏層,輸出層二分類常用sigmoid,多分類常用softmax
激活函數參數初始化
????????參數初始化在神經網絡訓練中扮演著至關重要的角色,它直接影響模型的收斂速度、訓練穩定性以及最終性能。
核心作用:
- 打破對稱性
????????若所有參數初始化為相同值(如零初始化),神經元在反向傳播時會接收到相同的梯度更新,導致網絡無法學習差異化特征。隨機初始化(如正態分布或均勻分布)通過賦予參數不同的初始值,確保神經元學習不同的特征.
- 控制梯度傳播穩定性
????????初始化值過大可能導致梯度爆炸(權重更新失控),過小則導致梯度消失(淺層參數無法更新)。例如,Xavier和Hekaiming初始化通過調整權重范圍,使各層輸出的方差保持一致,從而穩定梯度傳播
- 加速模型收斂?
????????合理的初始化(如Xavier或He初始化)能使網絡在訓練初期處于更優的起始狀態,減少收斂所需的迭代次數。
- 適配激活函數特性
????????不同激活函數對初始化范圍的要求不同,如:
????????Sigmoid/Tanh??:適合Xavier初始化,因其需要對稱的輸入分布
????????ReLU??:He初始化通過調整方差適應ReLU的“單側抑制”特性
常見初始化方式及對比

激活函數初始化選擇
模擬搭建神經網絡?如圖

+1為偏置,及z=wx+b的b?
是??偏置節點的可視化表示??,它通過引入可學習的偏置權重,幫助神經網絡擺脫輸入空間的限制,顯著提升模型的表達能力,它允許神經元的激活函數在輸入全為0時也能產生非零輸出,增強模型的靈活性。如果沒有偏置,許多簡單的分類問題(如異或問題)將無法被正確擬合。
?具體步驟如下
# 導包
from torch.nn import Module, Linear
import torch
# 提前安裝torchsummary,然后導入summary查看模型參數
# pip install torchsummary
from torchsummary import summary# TODO 1.自定義模型類繼承Module類
class My_Model(Module):# TODO 2.重寫init魔法方法和forward前向傳播方法def __init__(self, *args, **kwargs):# 1.調用父類的init初始化方法super().__init__(*args, **kwargs)# TODO 定義神經網絡結構self.linear1 = Linear(3, 3)self.linear2 = Linear(3, 2)self.out = Linear(2, 2)# 3.參數初始化(生成權重矩陣和偏置矩陣)# 隱藏層初始化權重矩陣torch.nn.init.xavier_normal_(self.linear1.weight)torch.nn.init.kaiming_normal_(self.linear2.weight)# 隱藏層初始化偏置矩陣torch.nn.init.zeros_(self.linear1.bias)torch.nn.init.zeros_(self.linear2.bias)def forward(self, x):# TODO 前向傳播計算(每層都是加權求和+激活函數)x = torch.sigmoid(self.linear1(x))x = torch.relu(self.linear2(x))# 此處-1代表最后一維, 也就是按照每個樣本概率和為1.x = torch.softmax(self.out(x), dim=-1)# 返回結果return x# TODO 3.創建模型對象并使用模型對象
# 創建模型對象
model = My_Model() # 自動調用init魔法方法
# 準備數據集(正態分布數據)
torch.manual_seed(66)
data = torch.randn(5, 3) # 5個樣本,3個特征
print(data)
# 把數據傳入模型對象
output = model(data) # 自動調用forward方法
print(output)
print('============================================================')
# TODO summary()查看模型參數
summary(model, (3,), batch_size=5) # 第1層:12,第2層:8,第3層:6
print('============================================================')
# TODO 遍歷查看模型名字和對應參數
for name, param in model.named_parameters():print(f'參數名稱: {name}, 參數值: {param}')print('---------------------------------')
損失函數
在機器學習中就已經引入了損失函數的概念,在此回顧一遍
? ? 損失函數是衡量模型參數質量的函數,又叫代價函數,誤差函數等等,根據損失函數計算損失值,結合反向傳播算法以及梯度下降算法實現參數的更新.(前向傳播和方向傳播在后續優化方法中會提到)
損失函數分為兩大類:
- 分類損失函數
- 多分類交叉熵損失函數:nn.CrossEntropyLoss(reduction='mean')? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????[實現softmax激活值計算+損失計算]
- 二分類交叉熵損失函數:nn.BCELoss(reduction='mean')
- 回歸損失函數:
- MAE平均絕對誤差損失函數:nn.MSEloss(),計算平均絕對誤差
- MSE均方誤差損失函數:nn.MSEloss(),計算均方誤差
- Huber Loss損失函數:指定a值,小于a使用MSE,大于a使用MAE使得損失值更平滑
- Smooth L1損失函數:a=1的Huber Loss損失函數
網絡模型優化方法 學習率 梯度 正則化
????????眾所周知,損失函數是衡量模型參數好壞的標準,而模型參數是通過梯度下降來進行更新的,也就是說,要優化模型,就是優化梯度下降算法,梯度下降公式為:

不難看出:僅有的兩個變量為學習率和梯度,梯度通常指損失函數關于模型參數的導數,因此優化方法需要從這倆入手
梯度下降法三大概念
epoch:訓練次數/輪次
batch_size:?每次迭代需要的樣本數
iteration:每次訓練需要迭代多少次:樣本數/batch_size[+1, 不能整除需要加1]
正向傳播與反向傳播
????????正向傳播(Forward Propagation)是神經網絡中數據從輸入層逐層傳遞到輸出層的過程。每一層的神經元接收前一層輸出的加權求和結果,并通過激活函數生成該層的輸出,最終得到網絡的預測結果。

????????反向傳播(Backpropagation)是訓練神經網絡的核心算法,用于計算損失函數對網絡參數的梯度。通過鏈式法則,梯度從輸出層反向傳播到輸入層,指導參數更新以最小化損失。

?反向梯度計算:

?參數更新:梯度= 損失值對網格參數w求導,顯而易見,梯度是逐級向上逐漸求出的,最終每一個梯度都會被更新,需要注意的是,梯度的計算路徑即反向傳播路徑不止一條.

梯度下降的兩種優化方式:梯度角度和學習率角度
指數加權平均思想:根據歷史指數加權值與當天值加權計算得出當前指數加權平均值
當處于第一天時,new歷史加權指數平均值==第一天的值
當處于第二天時,new歷史加權指數平均值=b*歷史加權平均值=(1-b)*第二天值
當處于第三天時,new歷史加權指數平均值=b*歷史加權平均值=(1-b)*第三天值
....
此思想是優化方法的核心思路


在梯度角度的優化方法
BGD 每次迭代時使用全部訓練數據計算損失函數的梯度,并更新模型參數 準但是慢
SGD?每次迭代僅使用一個樣本或一小批樣本來計算梯度 快但是不準
MBGD 選幾個梯度更新 不慢較準
momentum動量法?當前梯度是指數移動加權平均梯度
引入了指數加權平均思想?
梯度 ==?當前梯度*系數+歷史加權平均梯度*(1-系數)
St=(1-β)*Gt + β*St-1
在學習率角度優化的方法
- 自動調整
adagrad:自動調整學習率,初始大,后期小
新學習率=原始學習率/歷史梯度平方
?RMSprop:新學習率=舊學習率/歷史梯度加權平方
Adam:是RMSprop學習率更新+momentun梯度更新一起使用
- 手動調整
等間隔:lr = lr * gamma
scheduer = optim.lr_scheduler.StepLR(optimizer=optimizer, step_size=50, gamma=0.5)
指定間隔:lr = lr * gamma
optim.lr_scheduler.MultiStepLR(optimizer=optimizer, milestones=[50, 100, 160], gamma=0.5, last_epoch=-1)
指數衰減:lr = lr*gamma**epoch
optim.lr_scheduler.ExponentialLR(optimizer=optimizer, gamma=0.9)

優化器的選擇
深度學習默認選擇adam:適合大多數深度學習任務
SGD+momentum:更好的泛化性能,如cv任務
adagrad或者RMS適合用于稀疏數據或者特定任務
正則化
防止機器學習模型過擬合的技術,通過在損失函數中添加額外的懲罰項,限制模型參數的大小或復雜度。其核心目標是提高模型在未知數據上的泛化能力。
范數正則化
L1正則化(Lasso回歸)
L2正則化(嶺回歸)

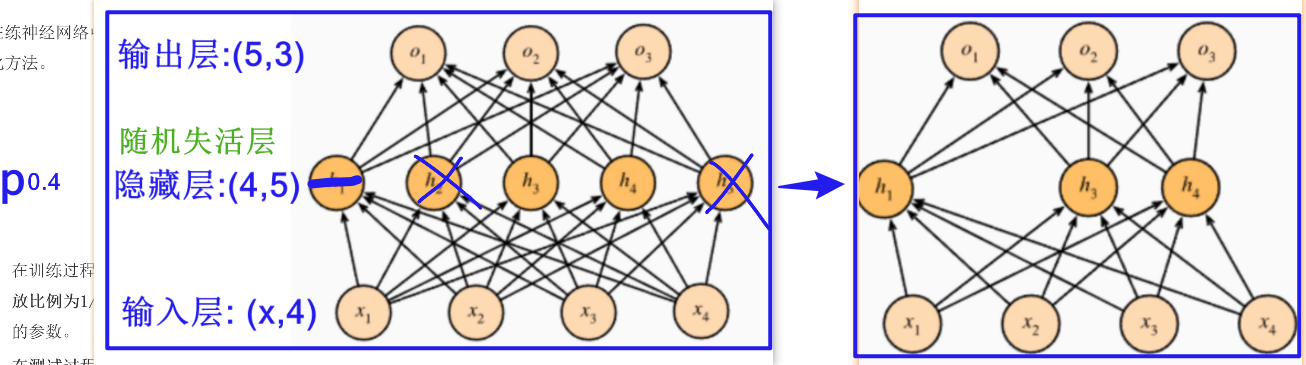
隨機失活正則化
dropout層?
以指定p概率讓神經元隨機失活
批量歸一正則化
實現原理:對線性結果進行標準化處理,?根據每批樣本的均值和標準差計算標準化的值
注意點
- ?? ?在激活層前使用(卷積層后/線性層后)
- ?? ?多數在計算機視覺領域使用
- ?? ?可以引入γ和β可學習參數, 不同層的樣本分布在不同范圍內(不同層使用的激活函數不同); 可以補回標準化丟失的信號



)

,通過word轉成pdf,放壓縮包)


)










,圖像的布爾類型圖例說明)
