本文主要講解七大排序算法之外的另一種排序算法 -- 計數排序?
目錄
1? 計數排序
1) 算法思想
2) 代碼?
3) 時間復雜度與空間復雜度分析?
(1) 時間復雜度
(2) 空間復雜度
4) 計數排序的優點與缺點
(1) 優點
(2) 缺點
2? 排序的穩定性
1) 穩定性的定義
2) 七大排序算法的穩定性分析
3) 七大排序算法時空復雜度與穩定性總結
3? 總結
1? 計數排序
????????計數排序是排序算法中最簡單的一種算法,不需要借助遞歸等算法,不過需要一點哈希表的思想(哈希表是一種數據結構,后面 C++ 部分會有相應的講解,本質就是通過一個函數將元素值轉化為其對應的映射,從而快速找到其值的一個數據結構)。
1) 算法思想
? ? ? ? 計數排序的算法思想如同其名字一樣,就是計算出其每個元素出現的次數,然后進行排序,其算法過程如下:
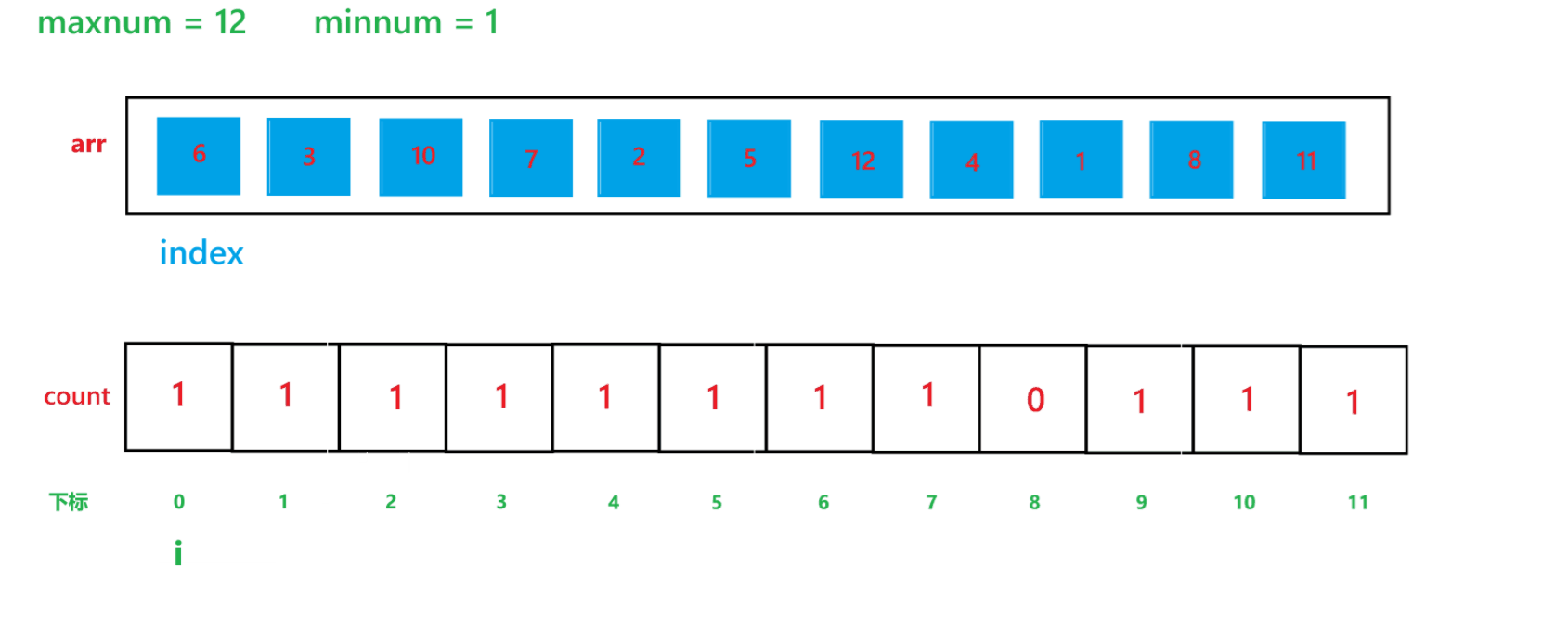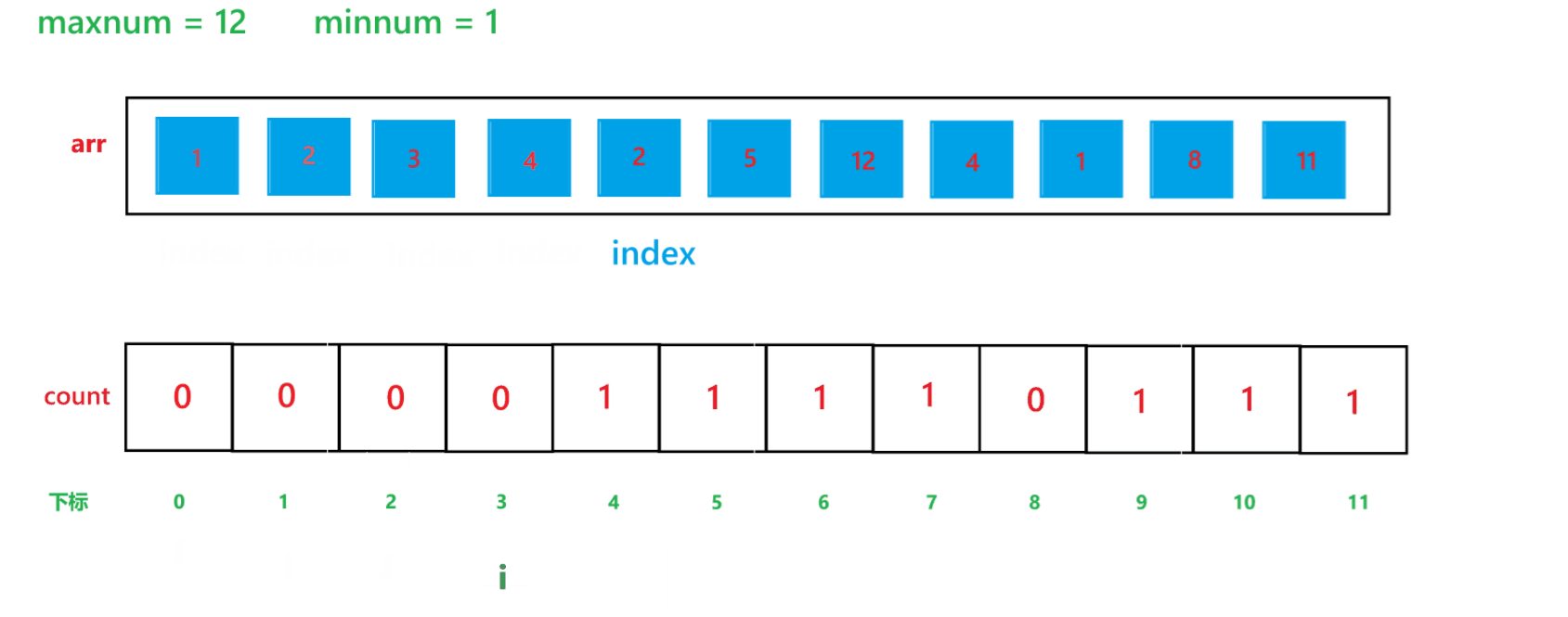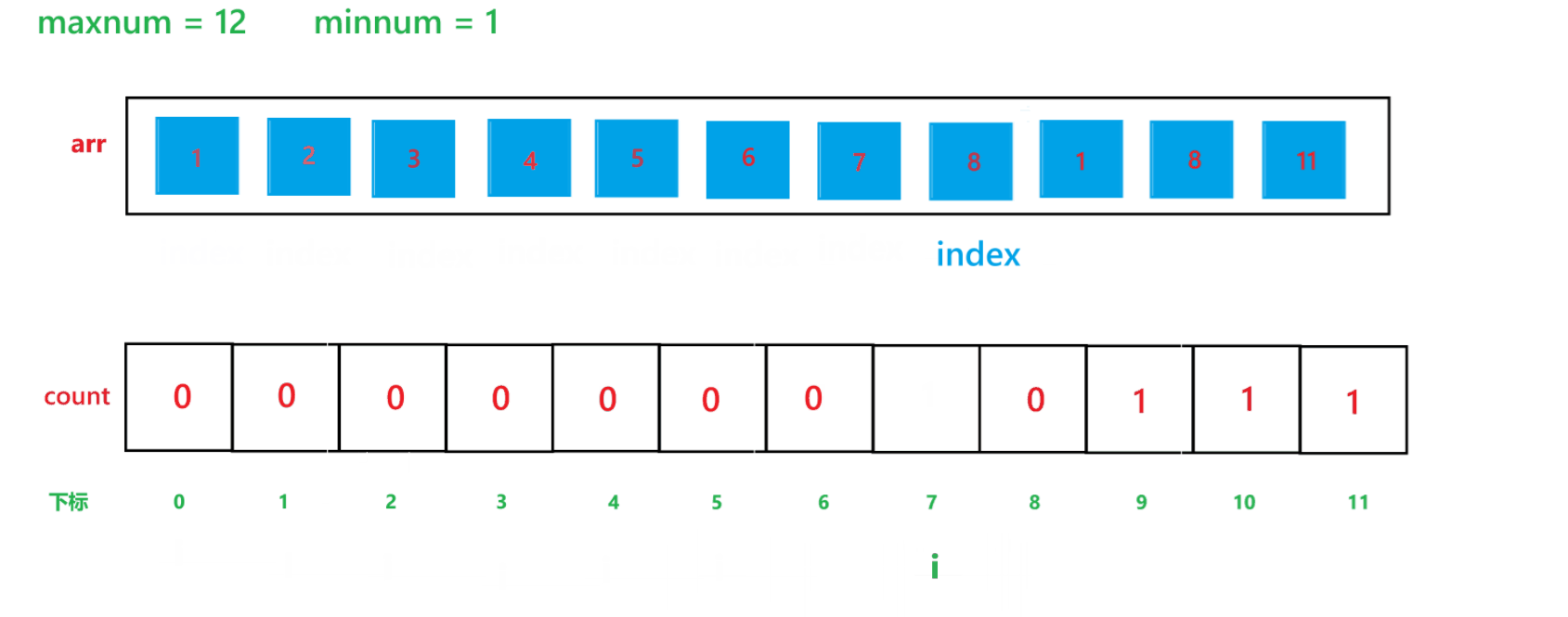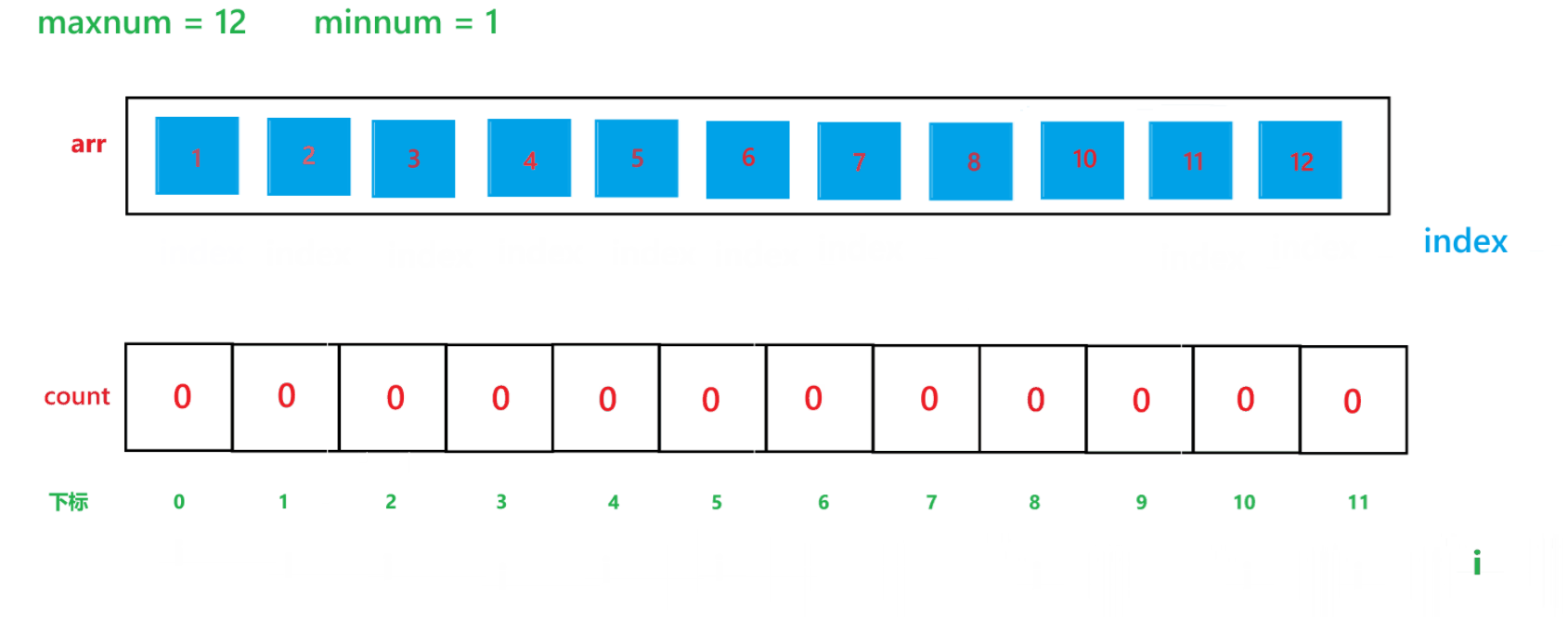
a. 先找出其數組中的最大值 maxnum 與 最小值 minnum,然后動態開辟一個 maxnum - minnum + 1 空間大小的數組 count
b. 然后用一個變量 i 遍歷原數組,假設原數組為 arr,然后每次讓 count[arr[i] - minnum]++
c. 再用一個變量 i 遍歷 count 數組,再創建一個 index 下標,初始為 0,如果 count[i] != 0,那就讓arr[index] = i + minnum,然后 index++,count[i]--,直到 count[i] 變為 0 為止。
其算法思想本質就是通過 arr 數組中每個元素減去最小值計算出 arr 數組中每個元素在 count 數組中的下標映射,然后越小的元素就在 count 數組中處于越前面的位置,count[i] 就記錄了每個元素出現的次數。其執行過程如下:
(1) count 數組變化的過程:
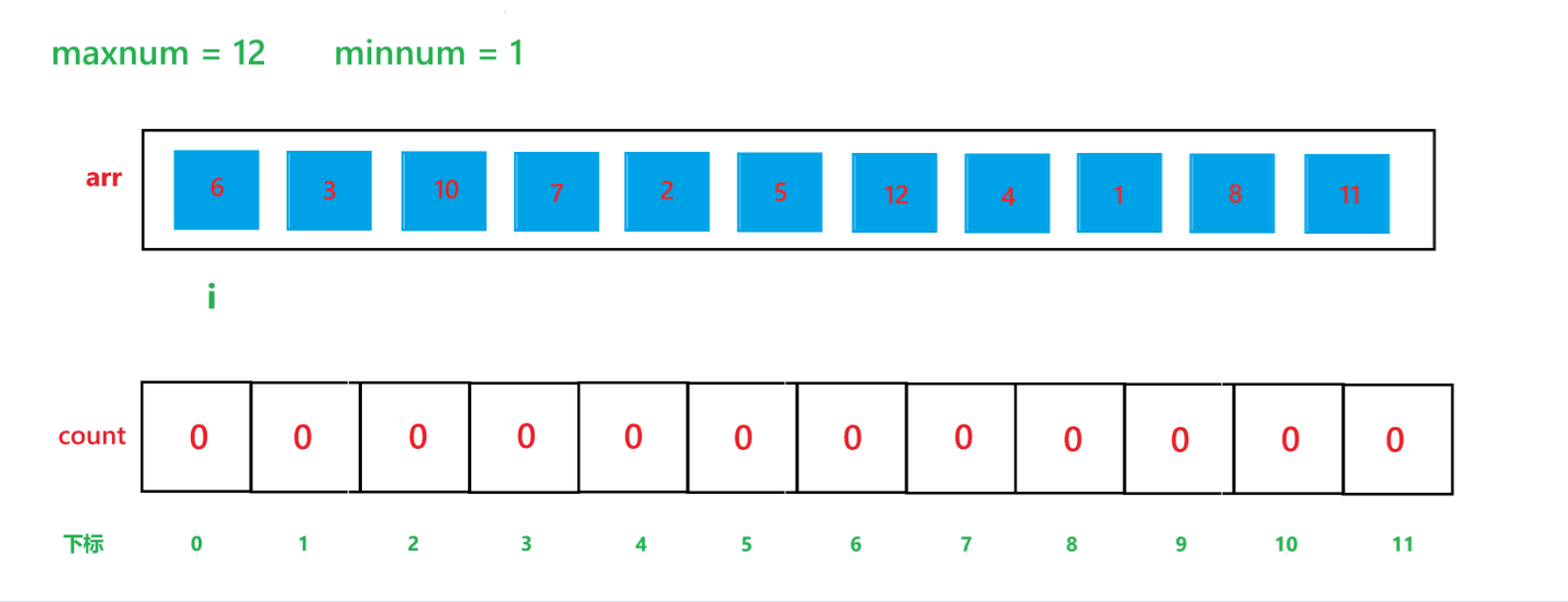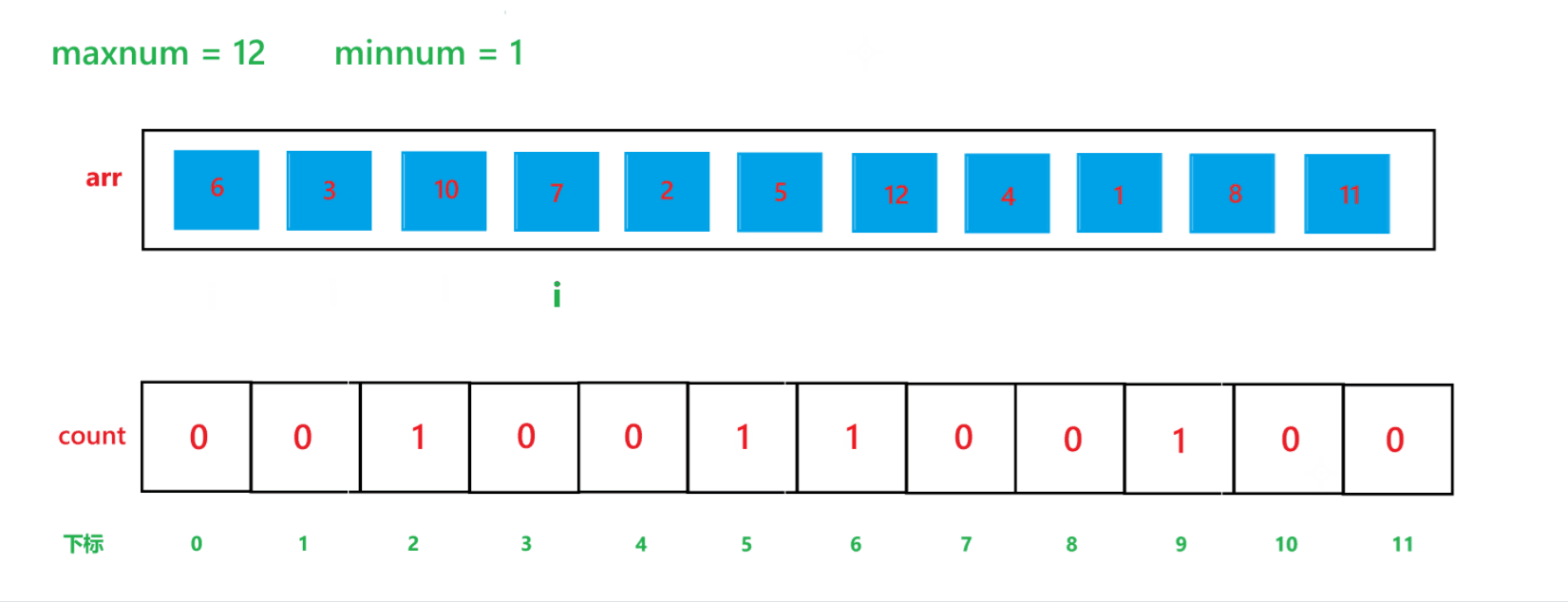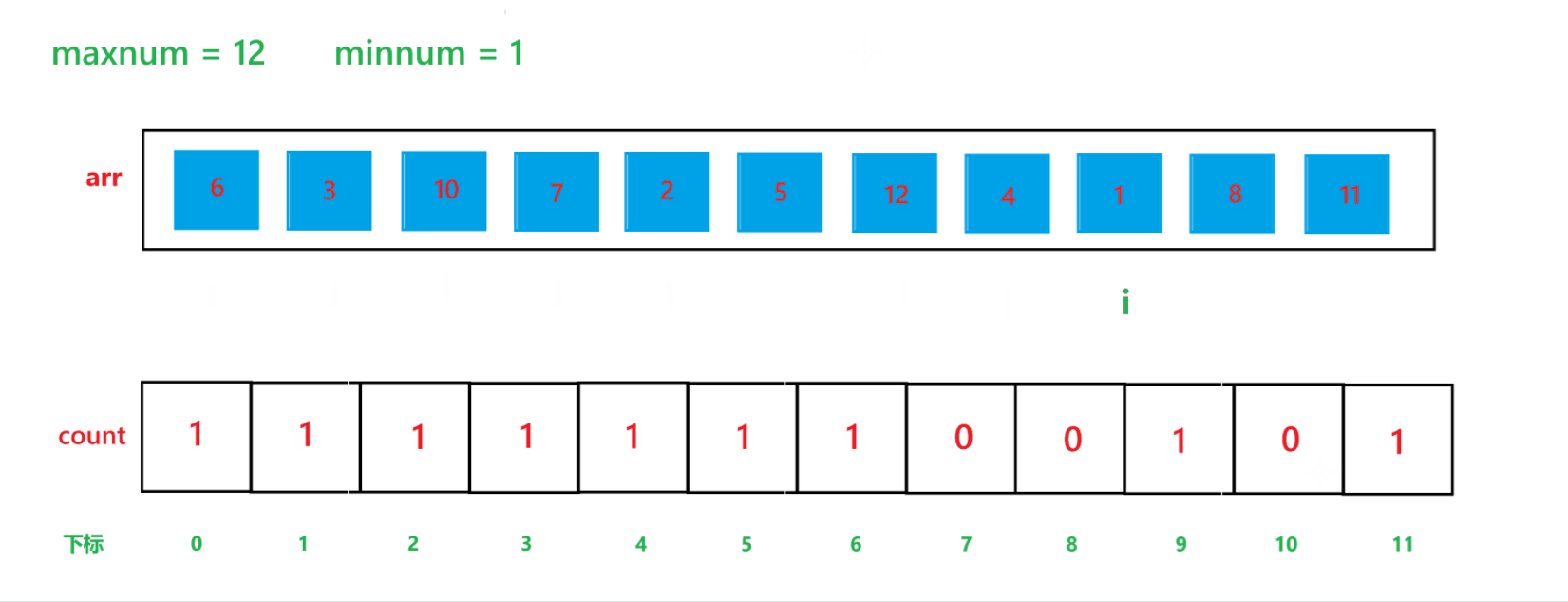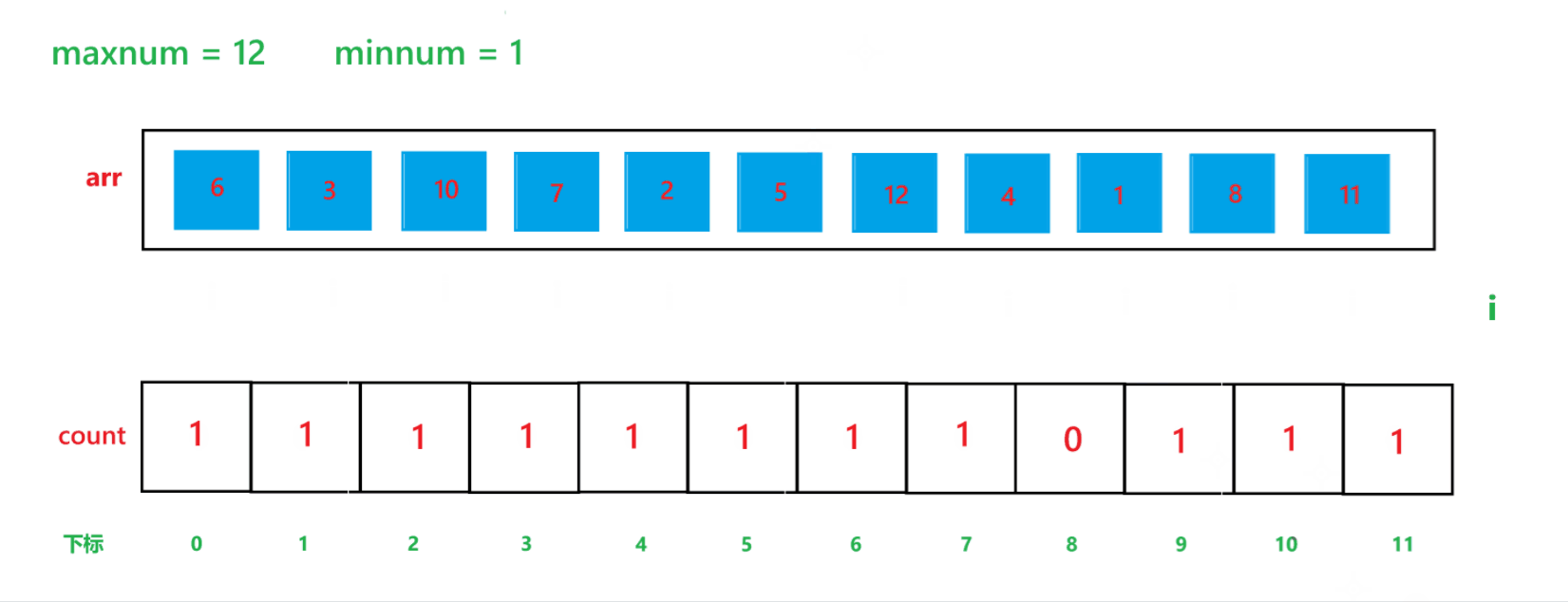
(2) arr 數組變化過程:
2) 代碼?
void CountSort(int* arr, int n)
{//先找最大值和最小值int maxnum = 0, minnum = INT_MAX;for (int i = 0; i < n; i++){if (maxnum < arr[i]) maxnum = arr[i];if (minnum > arr[i]) minnum = arr[i];}//開辟數組空間int* count = (int*)calloc(maxnum - minnum + 1, sizeof(int));if (count == NULL){perror("malloc fail!\n");exit(1);}//遍歷原數組,count記錄出現次數for (int i = 0; i < n; i++){count[arr[i] - minnum]++;}//再遍歷count數組,將元素放到 arr 數組中int index = 0;for (int i = 0; i < maxnum - minnum + 1; i++){while (count[i]){arr[index++] = i + minnum;count[i]--;}}
}這里有個需要注意的一點,就是動態開辟 count 數組空間的時候,要使用 calloc 函數,因為 count 數組里面的值必須全都初始化為 0,如果用 malloc 函數的話里面是隨機值,是會發生錯誤的。
測試用例:
#include<stdio.h>
#include<stdlib.h>int main()
{int arr[] = { 6, 3, 10, 7, 2, 5, 12, 4, 1, 8, 11 };int n = sizeof(arr) / sizeof(arr[0]);CountSort(arr, n);for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");return 0;
}3) 時間復雜度與空間復雜度分析?
(1) 時間復雜度
? ? ? ? 從代碼來分析,盡管有里面有兩層循環,但是里面的 count[i] 循環僅有常數次,假設這里的 maxnum - minnum + 1 = k,計數排序的時間復雜度為 T(n) = O(n + k)。
(2) 空間復雜度
? ? ? ? 假設 maxnum - minnum + 1 為 k,由于動態開辟了 k 個空間,所以空間復雜度為 S(n)?= O(k)。
4) 計數排序的優點與缺點
(1) 優點
? ? ? ? 計數排序的優點特別明顯,就是其時間復雜度比較低,執行效率很高;前面的七大排序算法最快的時間復雜度就是 O(nlogn),所以計數排序的執行效率是比前面任何一個排序的執行效率都快。
(2) 缺點
? ? ? ? 但是計數排序也有明顯的缺點,由于在排序過程中需要動態開辟 maxnum - minnum + 1 的空間,所以如果 maxnum 與 minnum 相差很大時,需要動態開辟的空間就很大,會浪費很多空間;所以如果 arr 數組中的數據相差很大,比較離散時,計數排序的消耗就會很大。
? ? ? ? 綜合來說,計數排序的應用場景比較有限,如果 arr 數組中的數據很集中時,應用計數排序就很合適,效率很高;但如果數據比較離散的話,計數排序就不太適合了,消耗會比較大。
2? 排序的穩定性
1) 穩定性的定義
? ? ? ? 一個排序算法是否穩定是指:如果對于一組數據,其中有相等的值,如果進行排序之后,之前相等的值的相對位置保持不變,那就稱該排序算法是穩定的,否則就是不穩定的。比如:有一組數據 1?8?5 8 7,假設第一個 8 為 num1,第二個數據為 num2,排序之前 num1 排在 num2 之前,排完序之后,該組數據變為 1 5 7 num1 num2,num1 還是排在 num2 之前,就稱該排序算法是穩定的;假如排完序之后,num1 排在了 num2 之后,那么該排序算法就是不穩定的。
2) 七大排序算法的穩定性分析
冒泡排序:假設一組數據為 8 8 2 1,第一個 8 為 num1,第二個 8 為 num2(num1 num2? 2 1),那么根據冒泡排序的算法思想,第一輪排序的結果應該為 num1 2?1?num2,第二輪為 2 1 num1 num2,第三輪排序結果為 1 2 num1 num2。經過排序之后,發現 num1 還是排在 num2 之前,所以冒泡排序算法是穩定的。
?直接插入排序:還是假設數據為 num1 num2? 2 1(同冒泡排序),經過第一輪排序,結果仍為 num1 num2 2 1,第二輪排序結果為 2 num1 num2 1,第三輪排序結果為 1 2 num1 num2。排完序之后,num1 依然排在 num2 之前,所以直接插入排序也是穩定的。
歸并排序:依然假設數據為 num1 num2? 2 1,num1 與 num2 合并之后依然是 num1 num2,2 與 1 合并之后結果為 1 2,然后兩個子數組再進行合并,結果為 1 2 num1 num2。排完序之后,num1 依然排在 num2 之前,所以歸并排序也是穩定的。
直接選擇排序:假設一組數據為 num1 8 num2? 2 9?(5 8 5 2 9),第一輪排序之后結果為 2 8 num2 num1 9,發現 num1 跑到 num2 之后了,所以直接選擇排序是不穩定的。究其原因,就是因為直接選擇排序會將最大的與每輪排序中的最后一個位置交換,將最小的和每輪排序中的第一個位置交換,就有能會使相同元素的相對位置發生變化。?
希爾排序:假設一組數據為 num1 8 2 num2??9?(5 8 2 5?9),第一輪排序 num1 2 9 一組,8 num2 一組,排完序之后結果就變為了 2? num2? num1? 8? 9,此時 num2 與 num1 相對位置發生了變化,所以希爾排序也是一種不穩定的排序算法。
堆排序:假設一組數據為 num1 ?num2? num3? num4?(2? 2? 2? 2),第一次排序會將 num1 與 num4交換(堆頂元素與最后一個元素交換),此時結果變為了 num4? num2? num3? num1,相對位置發生了變化,所以堆排序也是一種不穩定的排序算法。
快速排序:假設一組數據為 5? num1? num2? 4? num3? 8? 9? 10? 11(5? 3? 3? 4? 3? 8? 9? 10? 11),第一次排序,key值為 5,cur 在后面找比 5 小的元素然后和 ++prev 位置交換(雙指針算法找 key 值),所以第一次排序之后結果為 num3? num1? num2? 4? 5? 8? 9? 10? 11,此時相對位置發生了變化,所以快速排序算法也是一種不穩定的排序算法。
3) 七大排序算法時空復雜度與穩定性總結
?以下表格是對七大排序的時空復雜度以及穩定性的總結:
?
| 排序算法 | 時間復雜度 | 空間復雜度 | 穩定性 |
|---|---|---|---|
| 直接插入排序 | O(n^2) | O(1) | 穩定 |
| 直接選擇排序 | O(n^2) | O(1) | 不穩定 |
| 希爾排序 | O(n^1.3) | O(1) | 不穩定 |
| 冒泡排序 | O(n^2) | O(1) | 穩定 |
| 堆排序 | O(nlogn) | O(1) | 不穩定 |
| 快速排序 | O(nlogn) | O(logn) ~ O(n) | 不穩定 |
| 歸并排序 | O(nlogn) | O(n) | 穩定 |
3? 總結
? ? ? ? 到這里,初階數據結構的知識就已經結束了,我們來回顧一下:在初階數據結構里面,我們學習了順序表、鏈表、棧、隊列以及二叉樹這五種數據結構,學習了 8 種排序算法;不僅通過具體代碼實現了每個數據結構,而且還通過具體題目來加深了對于數據結構的理解,相信在學習完初階數據結構之后,代碼能力肯定會提升很多。
? ? ? ? 在之后,我們會開啟新的模塊的學習,包括 C++語言、Linux操作系統以及高階數據結構和各種經典算法,比如遞歸、回溯、動態規劃、雙指針算法等,在后面的文章中會交叉更新不同內容,后面的難度也肯定會呈不斷遞增的趨勢,但是只要繼續學下去,肯定就會收獲滿滿,所以不要放棄哦!





)

內存模型深度剖析)




)

)




