題目鏈接:

D-異或炸彈（easy）_牛客小白月賽95 (nowcoder.com)

題目：

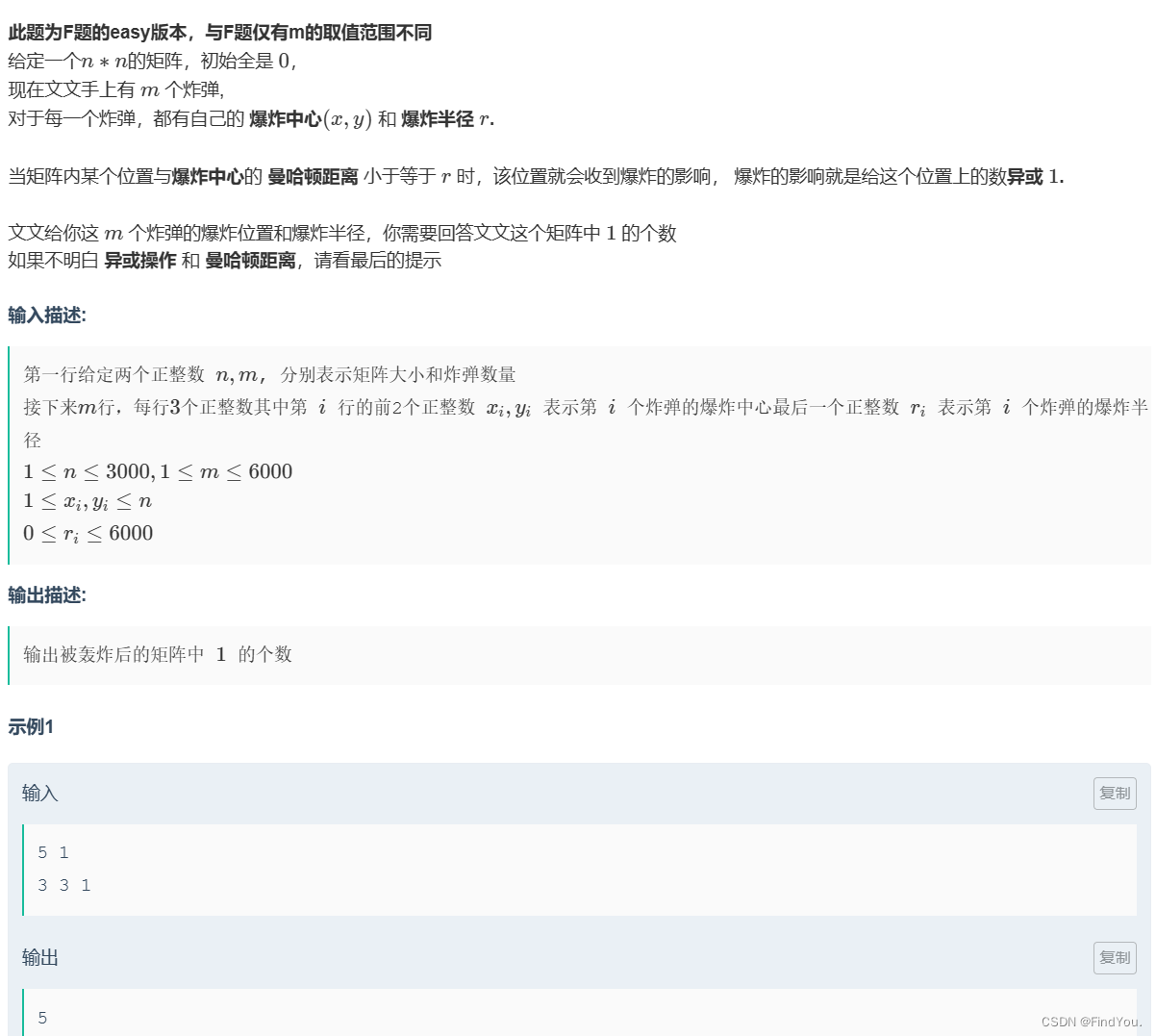
題目分析：

?一看 還以為是二維差分的題呢 到后來才發現是一維差分問題

這里的距離是?曼哈頓距離?dis = abs(x - xi) + abs(y - yi) 暴力的做法 就是枚舉 n * n 個點 然后看看這n * n 個點到m次詢問的點的距離是否小于等于r 但是時間復雜度為O(n *n * m )太高了 一定會TLE的其實發現 在每一行里面 滿足的都是一段連續的 那么差分就排上用場了 a[l] ++, a[r + 1] --?

枚舉每一行 也就是定一個x? 那么y的范圍也就出來了 因為 abs(x - xi) + abs(y - yi) <= r 那么 y 的范圍就是??yi - 剩余的(r - x到xi的距離) 到 yi + 剩余的(r - x到xi的距離) 這個y 就可以用差分去解決 注意邊界問題 以及絕對值

需要注意的是 下面的代碼里面的一個邊界?a[i][min(n + 1, y + dis + 1)] -- ;? 注意是 n + 1 要是寫成 n 的話 表示的意思 就是 y為n的這個點 就永遠取不到了 細節問題

代碼：

#include<bits/stdc++.h>
#define y1 Y1
#define fi first
#define endl "\n"
#define se second
#define PI acos(-1)
#define int long long
#define pb(x) push_back(x)
#define PII pair<int, int>
#define Yes cout << "Yes\n";
#define No cout << "No\n";
#define YES cout << "YES\n";
#define NO cout << "NO\n";
#define _for(i, a, b) for(int i = a; i <= b; ++i)
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;const int N = 3000 + 10;
const int mod = 1e9 + 7;int a[N][N];
int n, m, t, ret;
string s;signed main() {IOS;cin >> n >> m;while(m -- ) {int x, y, r;cin >> x >> y >> r;// 這里用的還是一維的差分的知識for(int i = max(1ll, x - r); i <= min(n, r + x); i ++ ) {int dis = r - abs(x - i); // 只要y在這個范圍內就可以a[i][max(1ll, y - dis)] ++ ;a[i][min(n + 1, y + dis + 1)] -- ; } }for(int i = 1; i <= n; i ++ ) {t = 0;for(int j = 1; j <= n; j ++ ) {t += a[i][j];if(t % 2 == 1)ret ++ ;}}cout << ret << endl;return 0;
}