組合總和
題目鏈接
39. 組合總和 - 力扣(LeetCode)
代碼:
class Solution {public List<List<Integer>> res = new ArrayList<>();public List<Integer> list = new ArrayList<>();public int sum = 0;/*** @param nums 目標數組* @param target 目標和* @param start 起始位置*/public void dfs(int[] nums, int target, int start) {//sum>=target就返回if (sum > target) {return;}if (sum == target) {res.add(new ArrayList<>(list));return;}for (int i = start; i < nums.length; i++) {list.add(nums[i]);//處理sum += nums[i];dfs(nums, target, i);//遞歸,注意這里是i(表示可以重復讀取當前的數)list.remove(list.size() - 1);//回溯sum -= nums[i];}}public List<List<Integer>> combinationSum(int[] candidates, int target) {dfs(candidates, target, 0);return res;}
}組合總和II
題目鏈接
40. 組合總和 II - 力扣(LeetCode)
本題的難點在于區別2中:集合(數組candidates)有重復元素,但還不能有重復的組合。
需要對同一層上的用過的數進行去重
如果candidates[i] == candidates[i - 1]?并且?used[i - 1] == false,就說明:前一個樹枝,使用了candidates[i - 1],也就是說同一樹層使用過candidates[i - 1]。
此時for循環里就應該做continue的操作。
這塊比較抽象,如圖:
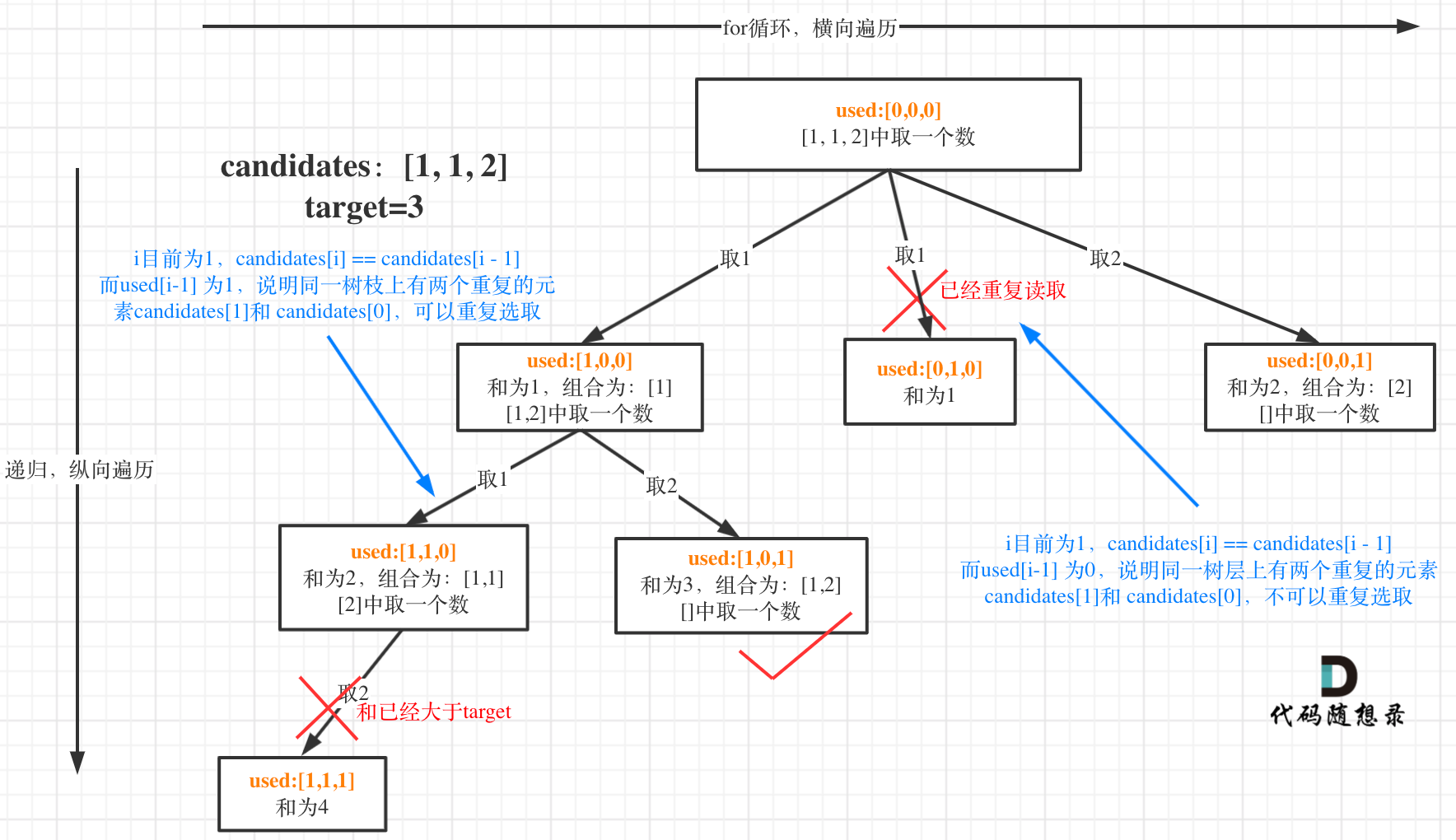
我在圖中將used的變化用橘黃色標注上,可以看出在candidates[i] == candidates[i - 1]相同的情況下:
- used[i - 1] == true,說明同一樹枝candidates[i - 1]使用過
- used[i - 1] == false,說明同一樹層candidates[i - 1]使用過
可能有的錄友想,為什么 used[i - 1] == false 就是同一樹層呢,因為同一樹層,used[i - 1] == false 才能表示,當前取的 candidates[i] 是從 candidates[i - 1] 回溯而來的。
而 used[i - 1] == true,說明是進入下一層遞歸,去下一個數,所以是樹枝上,如圖所示:
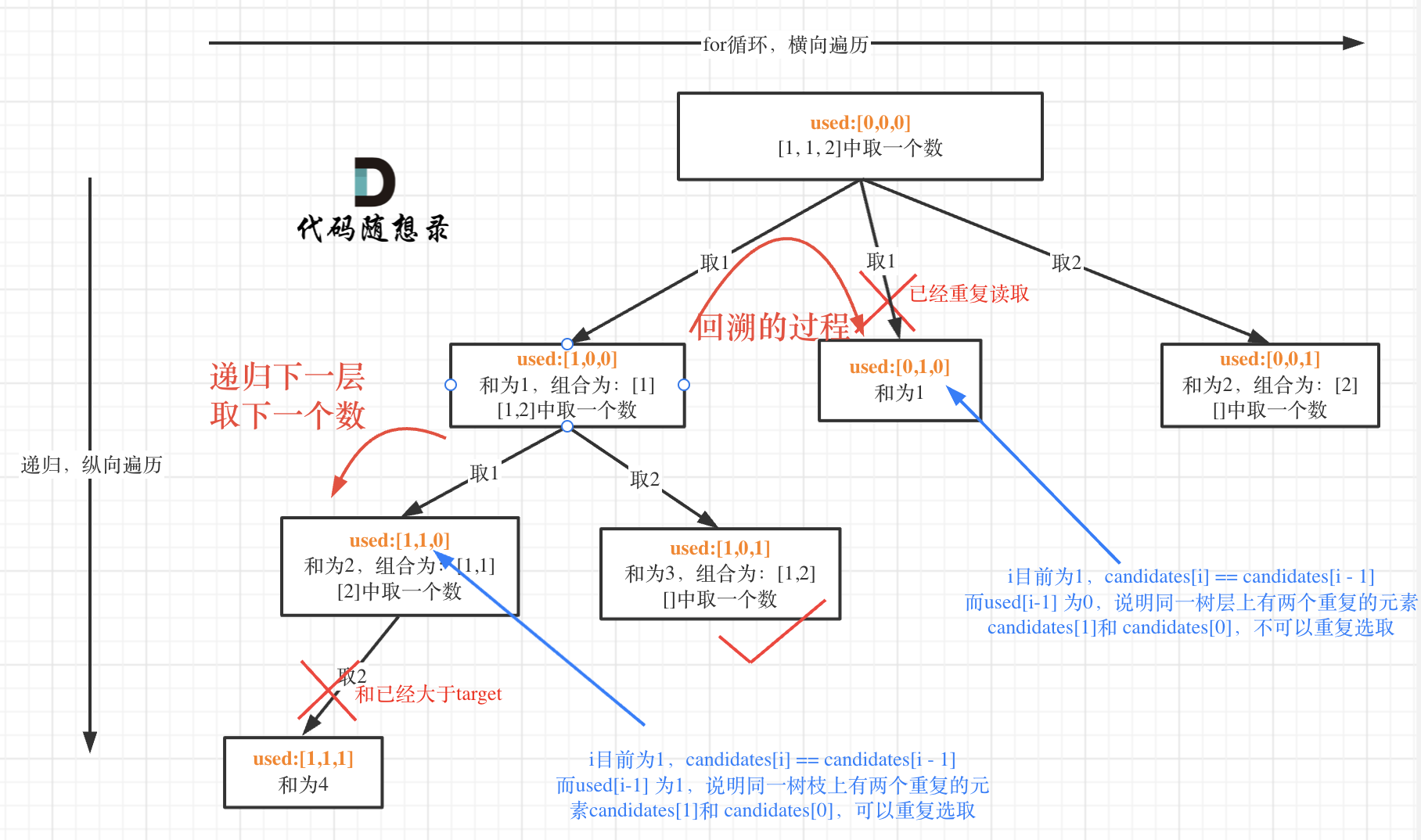
代碼:
class Solution {public List<List<Integer>> res = new ArrayList<>();public List<Integer> list = new ArrayList<>();public int sum = 0;/*** @param nums 目標數組* @param target 目標和* @param start 起始位置*/public void dfs(int[] nums, int target, int start) {//sum>=target就返回if (sum > target) {return;}if (sum == target) {res.add(new ArrayList<>(list));return;}for (int i = start; i < nums.length; i++) {if ( i > start && nums[i] == nums[i - 1] ) {//同一層不能重復取continue;}list.add(nums[i]);//處理sum += nums[i];dfs(nums, target, i + 1);//遞歸int temp=list.get(list.size()-1);sum-=temp;list.remove(list.size() - 1);//回溯}}public List<List<Integer>> combinationSum2(int[] candidates, int target) {Arrays.sort(candidates);dfs(candidates, target, 0);return res;}
}分割回文串
題目鏈接
131. 分割回文串 - 力扣(LeetCode)
利用回溯處理切割問題,
所以切割問題,也可以抽象為一棵樹形結構,如圖:

遞歸用來縱向遍歷,for循環用來橫向遍歷,切割線(就是圖中的紅線)切割到字符串的結尾位置,說明找到了一個切割方法。
代碼:
class Solution {public List<List<String>> res=new ArrayList<>();public List<String> list=new ArrayList<>();public boolean cheak(String s,int start,int end){for (int i = start,j=end; i <j ; i++,j--) {if(s.charAt(i)!=s.charAt(j)){return false;}}return true;}public void dfs(String s,int startIndex) {if (startIndex >= s.length()) {res.add(new ArrayList(list));return;}for (int i = startIndex; i < s.length(); i++) {//如果是回文子串,則記錄if (cheak(s, startIndex, i)) {String str = s.substring(startIndex, i + 1);list.add(str);} else {continue;}//起始位置后移,保證不重復dfs(s, i + 1);list.remove(list.size() - 1);}}public List<List<String>> partition(String s) {dfs(s, 0);return res;}
}

語法)



:requests模塊處理cookie)

)










