本篇文章我們將接著上篇繼續介紹常見的排序算法，有需要的小伙伴可以移步史上最全排序算法整理（1）查看相關內容哦

1.冒泡排序

1.1基本思想

在待排序的一組數中，將相鄰的兩個數進行比較，若前面的數比后面的數大就交換兩數，否則不交換；如此下去，直至最終完成排序。在排序過程中，大的數據往下沉，小的數據往上浮，就像氣泡一樣，于是將這種排序算法形象地稱為冒泡排序。

1.2特性總結

• 時間復雜度：O（N^2）
• 空間復雜度：O（1）
• 穩定性：穩定

1.3代碼實現

void BubbleSort(int* a, int n) 
{for (int j = 0; j < n - 1; j++){int exchange = 0;for (int i = 1; i < n - j; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

2.快速排序

2.1基本思想

快速排序是Hoare于1962年提出的一種二叉樹結構的交換排序方法。

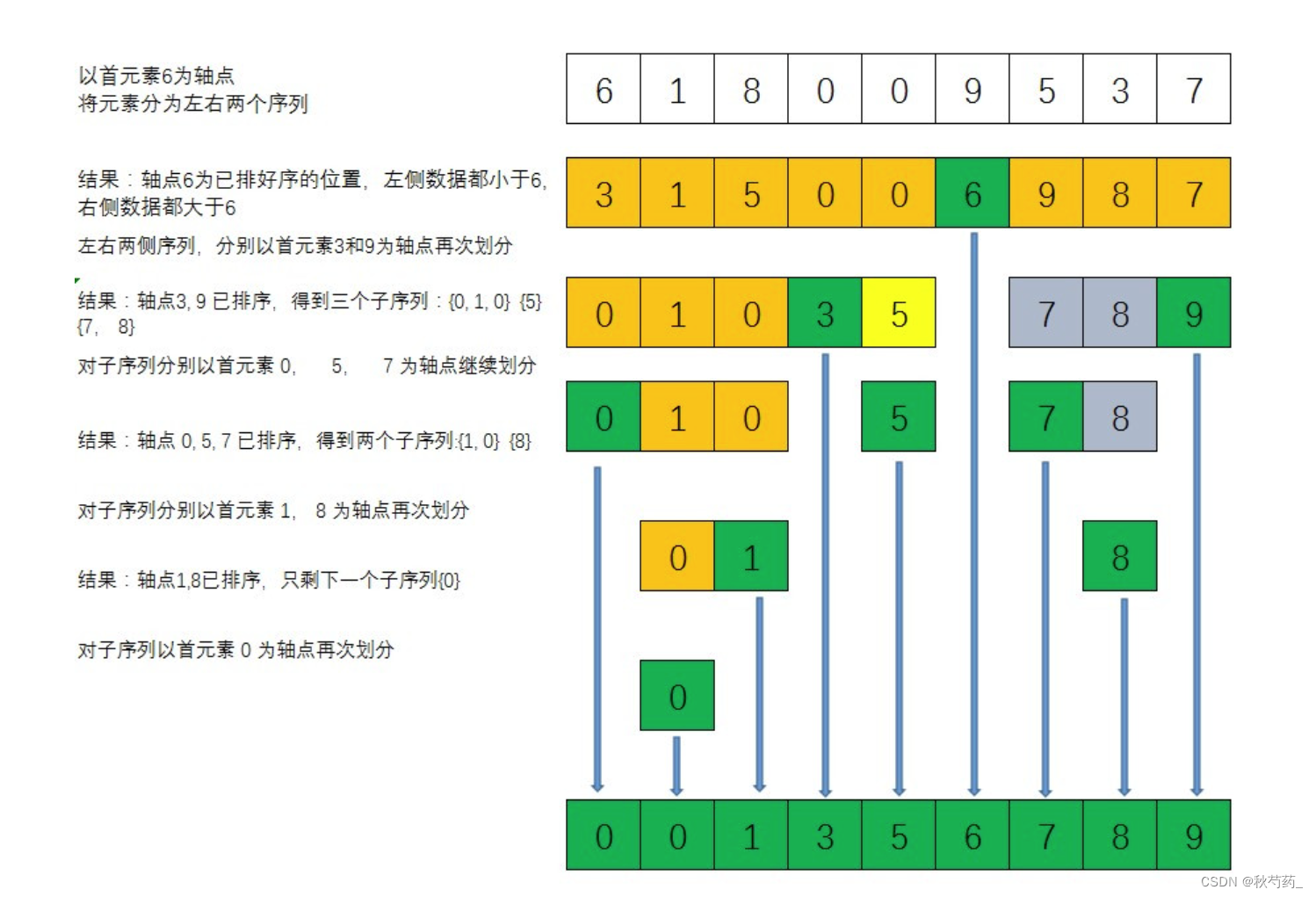
任取待排序元素序列中的某元素作為基準值，按照該排序碼將待排序集合分割成兩子序列，左子序列中所有元素均小于基準值，右子序列中的所有元素均大于基準值，然后對左右子序列重復該過程，直到所有元素都排列在相應的位置上為止。

2.2優化方法

選擇key時采用三數取中法

遞歸到小子區間的時候，考慮使用插入排序

2.3特性總結

• 時間復雜度：O（N*logN）
• 空間復雜度：O（logN）
• 穩定性：不穩定。其元素比較和交換是跳躍進行的，因此它是一種不穩定的排序算法。

2.4代碼實現

//快排三數取中
int GetMidi(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else//a[left]>=a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}//Hoare
void QuickSort1(int* a, int left, int right) 
{//區間只有一個值或者不存在的就是最小子問題if (left >= right)return;//小區間選擇走插入，可以減少90%左右的遞歸if (right - left + 1 < 10){InsertSort(a + left, right - left + 1);}else{int begin = left, end = right;int midi = Getmidi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;while (left < right){//right先走找小while (left < right && a[right] >= a[keyi]){right--;}while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;QuickSort1(a, begin, keyi - 1);QuickSort1(a, keyi + 1, end);}
}//快速排序-前后指針
void QuickSort2(int* a, int left, int right) 
{if (left >= right)return;int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[keyi], &a[prev]);keyi = prev;QuickSort2(a, left, keyi - 1);QuickSort2(a, keyi+1, right);
}

?3.歸并排序

3.1基本思想

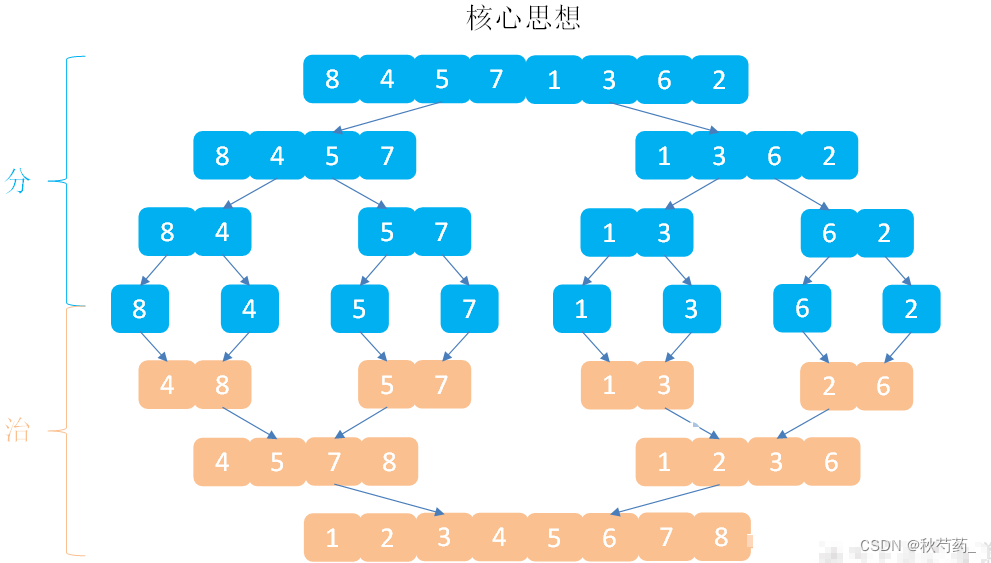
歸并排序是建立在歸并操作上的一種有效的排序算法，該算法是采用分治法的典型應用。將已有序的子序列合并，得到完全有序的序列

即先使每個子序列有序，再使子序列段間有序，若將兩個有序表合并成一個有序表，稱為二路歸并。

3.2特性總結

• 時間復雜度O（N*logN）?
• 空間復雜度O（N）
• 穩定性：穩定

3.3代碼實現

void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin == end)return;int mid = (begin + end) / 2;_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);int begin1 = begin, end1 = mid;int begin2 = mid + 1,end2 = mid;int i = begin;//依次比較，取較小的尾插while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end1){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
//歸并
void MergeSort(int* a, int n) 
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);tmp = NULL;
}

3.4歸并排序的非遞歸

?相比于遞歸算法，歸并排序的非遞歸算法不用多次調用同一個函數，不會向遞歸算法一樣因為函數嵌套調用次數太多而造成棧溢出。?相比于遞歸的算法，非遞歸與之不同點就一個：在遞歸中我們通過遞歸到最底層（即兩個數一組）進行排序，而非遞歸則是直接把數組分成兩個數一組進行排序，這邊排序完之后，再把數組分成四個一組排序，直到整個數組被分成兩組，排序后就結束。

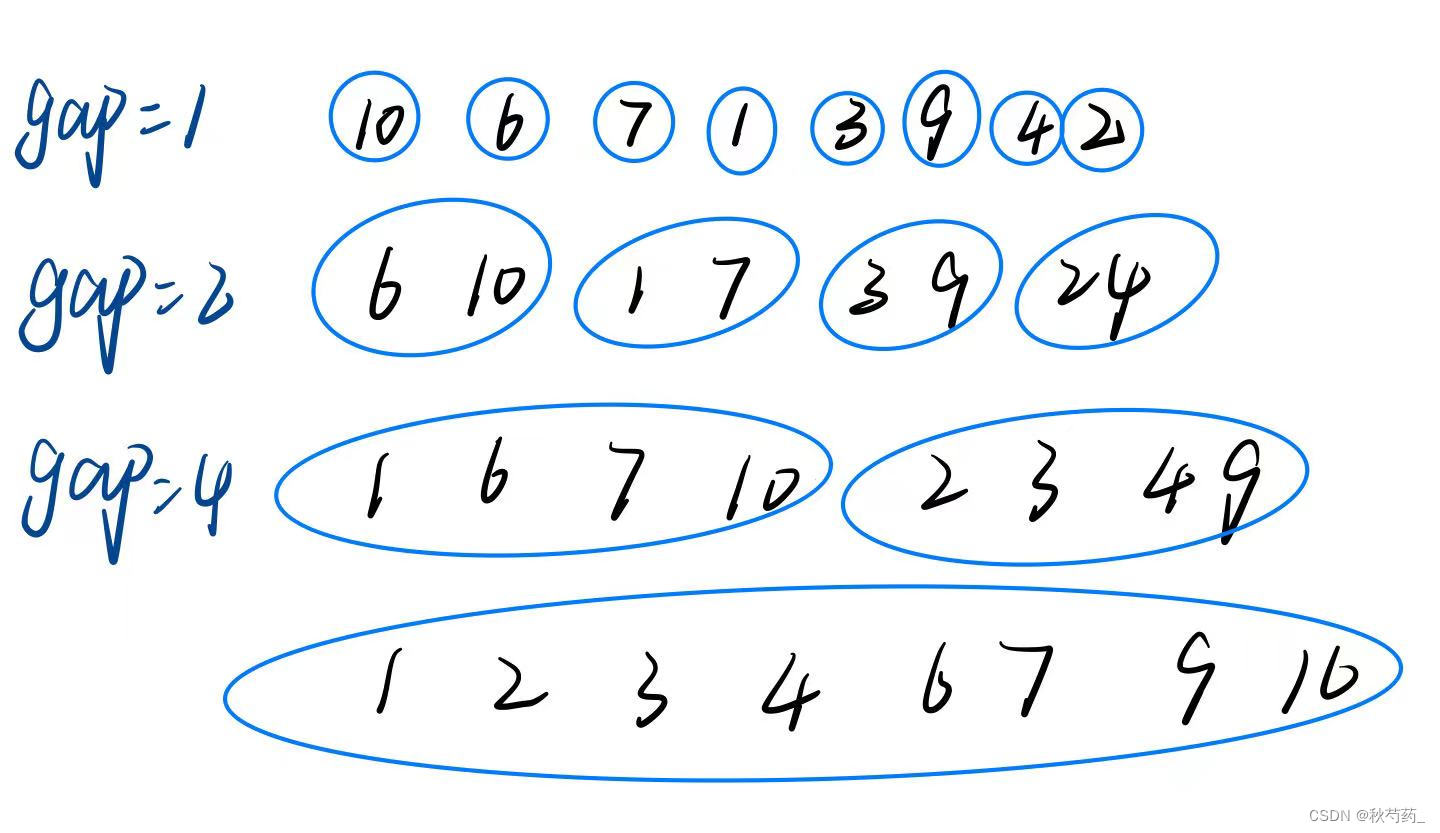
void MergeSortNonR(int* a, int n) 
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int j = 0; j < n; j += 2 * gap){int begin1 = j, end1 = begin1 + gap - 1;int begin2 = begin1 + gap, end2 = begin2 + gap - 1;//越界處理if (end1 >= n || begin2 >= n)break;if (end2 >= n)end2 = n - 1;int i = j;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end1){tmp[i++] = a[begin2++];}memcpy(a + j, tmp + j, sizeof(int) * (end2 - j + 1));}gap *= 2;}free(tmp);tmp = NULL;
}

4.非比較排序之計數排序

前面我們介紹的排序都是通過比較實現的，下面我們來看看一個常見的非比較排序

4.1基本思想

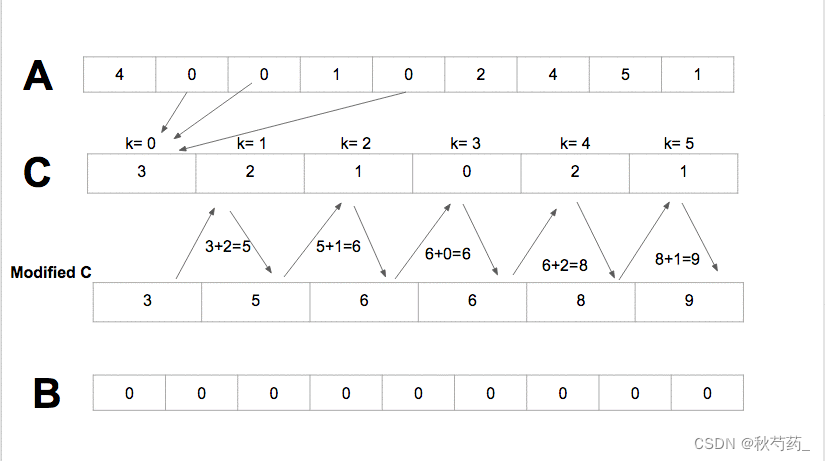
遍歷原數組，統計相同元素出現的個數，一個值出現了幾次，映射的位置次數就被增加幾，然后根據統計的結果將序列回收到原來的序列中。

4.2特性總結

• 計數排序在數據范圍集中地時候，效率很高，但是適用的范圍很有限
• 時間復雜度：O（MAX（N，范圍））
• 空間復雜度：O（范圍）?
• 穩定性：穩定

4.3代碼實現

void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 1; i < n; i++){if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];}int range = max - min + 1;//先根據最大值和最小值求出范圍int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail");return;}memeset(count, 0, sizeof(int) * range);for (int i = 0; i < n; i++){count[a[i] - min]++;}int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}

排序算法匯總

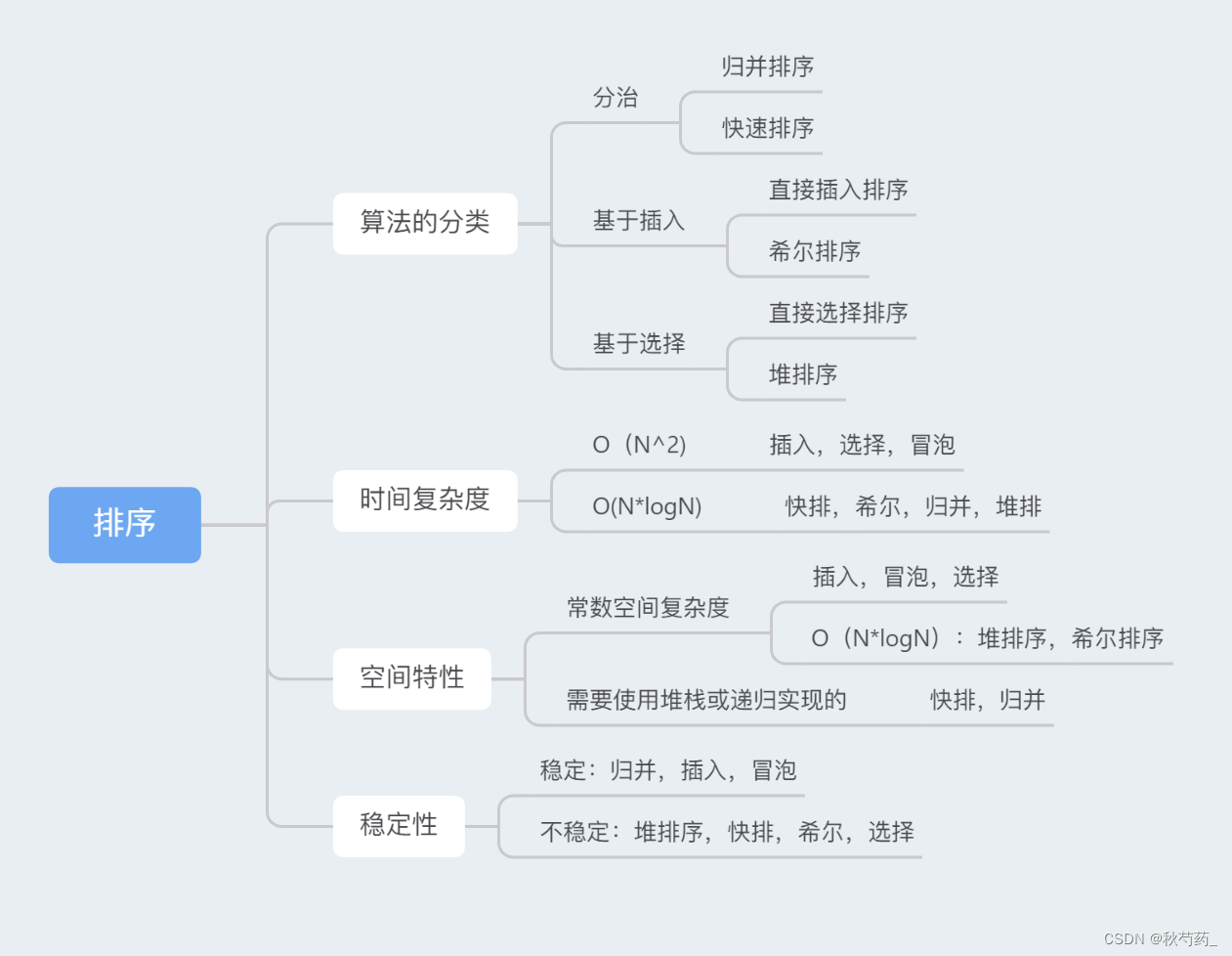
以上就是小編對排序算法的全部介紹啦

歡迎大家在評論區留言討論

點贊+評論+關注，是博主不斷更新優質文章的動力哦~