實驗的目的和要求：通過本次實驗使學生進一步熟悉掌握使用MATLAB軟件，并能利用該軟件進行無約束最優化方法的計算。
實驗內容：
１、最速下降法的MATLAB實現
２、牛頓法的MATLAB實現
３、共軛梯度法的MATLAB實現
學習建議：
本次實驗就是要通過對一些具體問題的分析進一步熟悉軟件的操作并加深對理論知識的理解。
重點和難點：
通過同一個具體問題用不同的方法解決的比較，加深理解恰當選用優化問題解決方法的重要性。
一 最速下降法
1.最速下降法基本原理和步驟
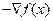思想：尋求最速下降方向即負梯度方向
MATLAB實現:
2.代碼及數值算例:
(1) 程序源代碼:
function [ X,FMIN,K ] = zuisuxiajiang( f,x,x0,e )% [ X,FMIN,N ] =zuisuxiajiang()法求解無約束問題% X 極小點% FMIN 極小值% K 迭代次數% f 問題函數% x 變量% x0 初始點% e 終止誤差% 張超編寫于2014/04/15 count=0;td=jacobian(f,x)';while norm(subs(td,x,x0))>eP=-subs(td,x,x0);syms ry=x0+r*P;ft(r)=subs(f,x,y); [r0]=fibonacci(ft,0,100,0.01);x0=x0+r0*P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
二 牛頓法
1.牛頓法基本原理和步驟
思想：在第k次迭代的迭代點x(k)鄰域內，用一個二次函數（如二階泰勒多項式）去近似代替原目標函數f(x)，然后求出該二次函數的極小點作為對原目標函數求優的下一個迭代點，依次類推，通過多次重復迭代，使迭代點逐步逼近原目標函數的極小點。
設*f(x)*二次連續可微，在點 x(k） 處的Hesse矩陣正定。
MATLAB實現:
2.代碼及數值算例:
(2) 程序源代碼:
function [ X,FMIN,K ] = ysNewton( f,x,x0,e )% [ X,FMIN,N ] =ysNewton()原始牛頓法求解無約束問題% X 極小點% FMIN 極小值% K 迭代次數% f 問題函數% x 變量% x0 初始點% e 終止誤差% 張超編寫于2014/04/15count=0;td=jacobian(f,x)';H=jacobian(td',x);while norm(subs(td,x,x0))>eP=-subs(H,x,x0)^(-1)*subs(td,x,x0);x0=x0+P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
牛頓法對于二次正定函數只需做一次迭代就得到最優解。特別在極小點附近，收斂性很好速度也很快。
但牛頓法也有缺點，它要求初始點離最優解不遠，若初始點選的離最優解太遠時，牛頓法并不能保證其收斂，甚至也不是下降方向。
為了克服牛頓法的缺點，人們保留了從牛頓法中選取牛頓方向作為搜索方向，摒棄其步長恒取1的作法，而用一維搜索確定最優步長來構造算法。
(3) 程序源代碼:
function [ X,FMIN,K ] = xzNewton( f,x,x0,e )% [ X,FMIN,N ] =xzNewton()帶步長牛頓法求解無約束問題% X 極小點% FMIN 極小值% K 迭代次數% f 問題函數% x 變量% x0 初始點% e 終止誤差% 張超編寫于2014/04/15count=0;td=jacobian(f,x)';H=jacobian(td',x);while norm(subs(td,x,x0))>eP=-subs(H,x,x0)^(-1)*subs(td,x,x0);syms ry=x0+r*P;ft(r)=subs(f,x,y); [r0]=fibonacci(ft,0,100,0.01);x0=x0+r0*P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
三 共軛梯度法
1.共軛梯度法基本原理和步驟
思想：將共軛性和最速下降方向相結合，利用已知迭代點處的梯度方向構造一組共軛方向，并沿此方向進行搜索，求出函數的極小點。
MATLAB實現:
2.代碼及數值算例:
(1) 程序源代碼:
function [ X,FMIN,K ] = gongetidu( f,x,x0,e )% [ X,FMIN,N ] =gongetidu()共軛梯度法求解無約束問題% X 極小點% FMIN 極小值% K 迭代次數% f 問題函數% x 變量% x0 初始點% e 終止誤差% 張超編寫于2014/04/15count=1;td=jacobian(f,x)';H=jacobian(td',x);if norm(subs(td,x,x0))>eP=-subs(td,x,x0);r0=-subs(td,x,x0)'*P/(P'*H*P);x0=x0+r0*P;else x0;endwhile norm(double(subs(td,x,x0)))>eb0=subs(td,x,x0)'*subs(td,x,x0)/(P'*P);P=-subs(td,x,x0)+b0*P;r0=-subs(td,x,x0)'*P/(P'*H*P);x0=x0+r0*P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
四 一個算例
分別用上述三中方法計算下題,并比較各算法.
Min f(x)=(x1 - 2)^2 + (x1 – 2*x2)^2
初始點x0=(0,3)T
允許誤差e=0.1
鍵入命令并輸出結果：
syms x1 x2\>> f=(x1-2)^2+(x1-2*x2)^2;\>> x=[x1;x2];\>> x0=[0;3];\>> e=0.1;[X,FMIN,N]=zuisuxiajiang(f,x,x0,e)X =1.97630.9818FMIN =7.2076e-04N =10\>> [X,FMIN,N]=ysNewton(f,x,x0,e)X =21FMIN =0N =1[X,FMIN,N]=gongetidu(f,x,x0,e)X =21FMIN =0N =2
由上述結果我們發現：
對于二次正定函數newton法只需一次迭代就得到正確結果，共軛梯度法只需進行兩次（因為目標函數是二元函數）迭代就得出正確結果。但最速下降法卻迭代了10次，雖然一維搜索存在誤差，但實際上最速下降法也需迭代多次。
