目錄

DAY42

1049.最后一塊石頭的重量II

解題思路&代碼

494.目標和

解題思路&代碼

474.一和零

解題思路&代碼

---

DAY42

1049.最后一塊石頭的重量II

力扣題目鏈接(opens new window)

題目難度：中等

有一堆石頭，每塊石頭的重量都是正整數。

每一回合，從中選出任意兩塊石頭，然后將它們一起粉碎。假設石頭的重量分別為?x 和?y，且?x <= y。那么粉碎的可能結果如下：

如果?x == y，那么兩塊石頭都會被完全粉碎；

如果?x != y，那么重量為?x?的石頭將會完全粉碎，而重量為?y?的石頭新重量為?y-x。

最后，最多只會剩下一塊石頭。返回此石頭最小的可能重量。如果沒有石頭剩下，就返回 0。

示例：

• 輸入：[2,7,4,1,8,1]
• 輸出：1

解釋：

• 組合 2 和 4，得到 2，所以數組轉化為 [2,7,1,8,1]，
• 組合 7 和 8，得到 1，所以數組轉化為 [2,1,1,1]，
• 組合 2 和 1，得到 1，所以數組轉化為 [1,1,1]，
• 組合 1 和 1，得到 0，所以數組轉化為 [1]，這就是最優值。

解題思路&代碼

思路：

關鍵點：認識到什么是應用類背包問題，此處如何聯系到背包？盡量把容器分成大小相等的兩堆，則另一堆是否能用數組元素填滿多少則是涉及到了背包最多能裝多少的問題

本題其實就是盡量讓石頭分成重量相同的兩堆，相撞之后剩下的石頭最小，這樣就化解成01背包問題了。

是不是感覺和昨天講解的416. 分割等和子集?(opens new window)非常像了。

本題物品的重量為stones[i]，物品的價值也為stones[i]。

對應著01背包里的物品重量weight[i]和 物品價值value[i]。

1.確定dp數組以及下標的含義

dp[j]表示容量（這里說容量更形象，其實就是重量）為j的背包，最多可以背最大重量為dp[j]。

可以回憶一下01背包中，dp[j]的含義，容量為j的背包，最多可以裝的價值為 dp[j]。

2.確定遞推公式

01背包的遞推公式為：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

本題則是：dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);

3.dp數組如何初始化

既然 dp[j]中的j表示容量，那么最大容量（重量）是多少呢，就是所有石頭的重量和。

因為提示中給出1 <= stones.length <= 30，1 <= stones[i] <= 1000，所以最大重量就是30 * 1000 。

而我們要求的target其實只是最大重量的一半，所以dp數組開到15000大小就可以了

4.確定遍歷順序

在動態規劃：關于01背包問題，你該了解這些！（滾動數組）?(opens new window)中就已經說明：如果使用一維dp數組，物品遍歷的for循環放在外層，遍歷背包的for循環放在內層，且內層for循環倒序遍歷！

• 時間復雜度：O(m × n) , m是石頭總重量（準確的說是總重量的一半），n為石頭塊數
• 空間復雜度：O(m)

class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0;for (int i : stones) {sum += i;}int target = sum >> 1;//初始化dp數組int[] dp = new int[target + 1];//為什么要+1，因為涉及到背包重量為0的情況，要初始化，但是實際上數組元素是不包括這個的for (int i = 0; i < stones.length; i++) {//采用倒序for (int j = target; j >= stones[i]; j--) {//兩種情況，要么放，要么不放dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[target];}
}

494.目標和

力扣題目鏈接(opens new window)

難度：中等

給定一個非負整數數組，a1, a2, ..., an, 和一個目標數，S。現在你有兩個符號?+?和?-。對于數組中的任意一個整數，你都可以從?+?或?-中選擇一個符號添加在前面。

返回可以使最終數組和為目標數 S 的所有添加符號的方法數。

示例：

• 輸入：nums: [1, 1, 1, 1, 1], S: 3
• 輸出：5

解釋：

• -1+1+1+1+1 = 3
• +1-1+1+1+1 = 3
• +1+1-1+1+1 = 3
• +1+1+1-1+1 = 3
• +1+1+1+1-1 = 3

一共有5種方法讓最終目標和為3。

?

解題思路&代碼

思路：

本題要如何使表達式結果為target，

既然為target，那么就一定有 left組合 - right組合 = target。

left + right = sum，而sum是固定的。right = sum - left

公式來了， left - (sum - left) = target 推導出 left = (target + sum)/2 。

target是固定的，sum是固定的，left就可以求出來。

此時問題就是在集合nums中找出和為left的組合

再回歸到01背包問題，為什么是01背包呢？

因為每個物品（題目中的1）只用一次！

這次和之前遇到的背包問題不一樣了，之前都是求容量為j的背包，最多能裝多少。

本題則是裝滿有幾種方法。其實這就是一個組合問題了。

1.確定dp數組以及下標的含義

dp[j] 表示：填滿j（包括j）這么大容積的包，有dp[j]種方法

其實也可以使用二維dp數組來求解本題，dp[i][j]：使用 下標為[0, i]的nums[i]能夠湊滿j（包括j）這么大容量的包，有dp[i][j]種方法。

2.確定遞推公式

有哪些來源可以推出dp[j]呢？

只要搞到nums[i]，湊成dp[j]就有dp[j - nums[i]] 種方法。

例如：dp[j]，j 為5，

• 已經有一個1（nums[i]） 的話，有 dp[4]種方法 湊成 容量為5的背包。
• 已經有一個2（nums[i]） 的話，有 dp[3]種方法 湊成 容量為5的背包。
• 已經有一個3（nums[i]） 的話，有 dp[2]中方法 湊成 容量為5的背包
• 已經有一個4（nums[i]） 的話，有 dp[1]中方法 湊成 容量為5的背包
• 已經有一個5 （nums[i]）的話，有 dp[0]中方法 湊成 容量為5的背包

那么湊整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起來。

所以求組合類問題的公式，都是類似這種：

dp[j] += dp[j - nums[i]]

3.dp數組如何初始化

從遞推公式可以看出，在初始化的時候dp[0] 一定要初始化為1，因為dp[0]是在公式中一切遞推結果的起源，如果dp[0]是0的話，遞推結果將都是0。

如果數組[0] ，target = 0，那么 bagSize = (target + sum) / 2 = 0。 dp[0]也應該是1， 也就是說給數組里的元素 0 前面無論放加法還是減法，都是 1 種方法。

所以本題我們應該初始化 dp[0] 為 1。

4.確定遍歷順序

在動態規劃：關于01背包問題，你該了解這些！（滾動數組）?(opens new window)中，我們講過對于01背包問題一維dp的遍歷，nums放在外循環，target在內循環，且內循環倒序。

5.舉例推導dp數組

輸入：nums: [1, 1, 1, 1, 1], S: 3

bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4

dp數組狀態變化如下：

• 時間復雜度：O(n × m)，n為正數個數，m為背包容量
• 空間復雜度：O(m)，m為背包容量

class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int i = 0; i < nums.length; i++) sum += nums[i];//如果target的絕對值大于sum，那么是沒有方案的if (Math.abs(target) > sum) return 0;//如果(target+sum)除以2的余數不為0，也是沒有方案的if ((target + sum) % 2 == 1) return 0;int bagSize = (target + sum) / 2;int[] dp = new int[bagSize + 1];dp[0] = 1;for (int i = 0; i < nums.length; i++) {for (int j = bagSize; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[bagSize];}
}

474.一和零

力扣題目鏈接(opens new window)

給你一個二進制字符串數組 strs 和兩個整數 m 和 n 。

請你找出并返回 strs 的最大子集的大小，該子集中 最多 有 m 個 0 和 n 個 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1：

• 輸入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3

• 輸出：4

• 解釋：最多有 5 個 0 和 3 個 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。 其他滿足題意但較小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不滿足題意，因為它含 4 個 1 ，大于 n 的值 3 。

解題思路&代碼

思路：

本題并不是多重背包，再來看一下這個圖，捋清幾種背包的關系

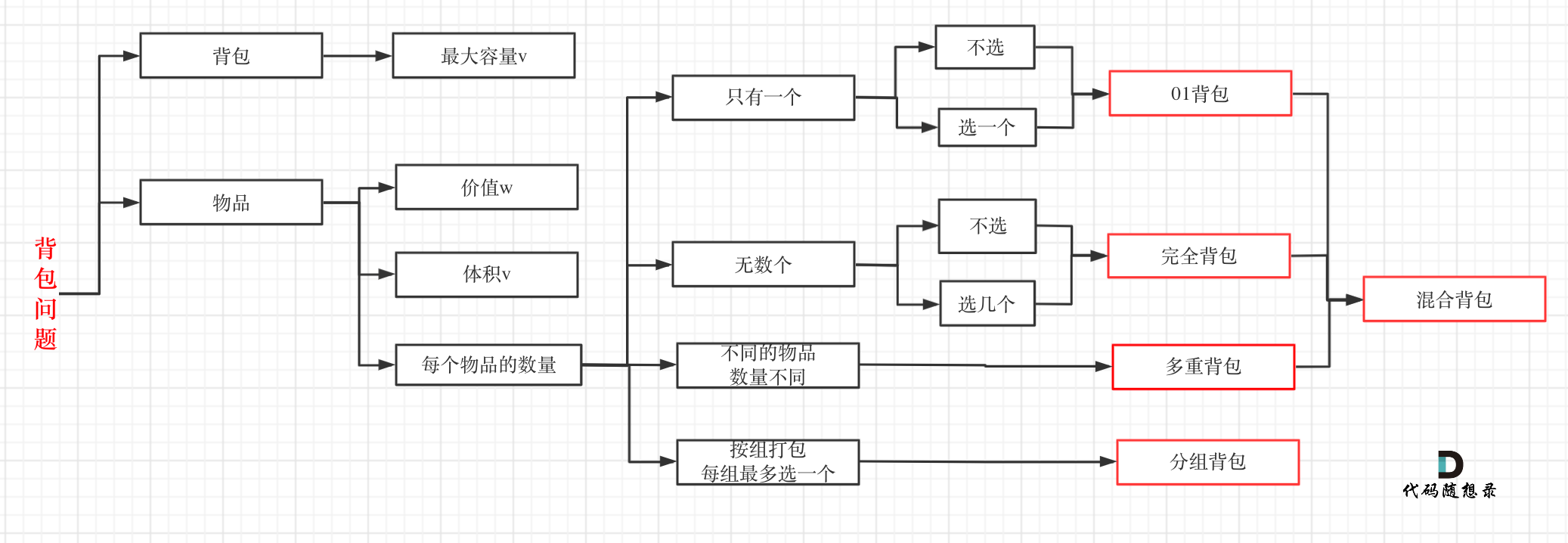
多重背包是每個物品，數量不同的情況。

本題中strs 數組里的元素就是物品，每個物品都是一個！

而m 和 n相當于是一個背包，兩個維度的背包。

理解成多重背包的同學主要是把m和n混淆為物品了，感覺這是不同數量的物品，所以以為是多重背包。

但本題其實是01背包問題！

只不過這個背包有兩個維度，一個是m 一個是n，而不同長度的字符串就是不同大小的待裝物品。

1.確定dp數組（dp table）以及下標的含義

dp[i][j]：最多有i個0和j個1的strs的最大子集的大小為dp[i][j]。

2.確定遞推公式

dp[i][j] 可以由前一個strs里的字符串推導出來，strs里的字符串有zeroNum個0，oneNum個1。

dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。

然后我們在遍歷的過程中，取dp[i][j]的最大值。

所以遞推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

此時大家可以回想一下01背包的遞推公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

對比一下就會發現，字符串的zeroNum和oneNum相當于物品的重量（weight[i]），字符串本身的個數相當于物品的價值（value[i]）。

這就是一個典型的01背包！?只不過物品的重量有了兩個維度而已。

3.dp數組如何初始化

在動態規劃：關于01背包問題，你該了解這些！（滾動數組）?(opens new window)中已經講解了，01背包的dp數組初始化為0就可以。

因為物品價值不會是負數，初始為0，保證遞推的時候dp[i][j]不會被初始值覆蓋。

4.確定遍歷順序

在動態規劃：關于01背包問題，你該了解這些！（滾動數組）?(opens new window)中，我們講到了01背包為什么一定是外層for循環遍歷物品，內層for循環遍歷背包容量且從后向前遍歷！

那么本題也是，物品就是strs里的字符串，背包容量就是題目描述中的m和n。

• 時間復雜度: O(kmn)，k 為strs的長度
• 空間復雜度: O(mn)?

class Solution {public int findMaxForm(String[] strs, int m, int n) {//dp[i][j]表示i個0和j個1時的最大子集int[][] dp = new int[m + 1][n + 1];int oneNum, zeroNum;for (String str : strs) {//正序遍歷物品oneNum = 0;zeroNum = 0;for (char ch : str.toCharArray()) {if (ch == '0') {zeroNum++;} else {oneNum++;}}//倒序遍歷背包容量for (int i = m; i >= zeroNum; i--) {for (int j = n; j >= oneNum; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
}