一，關于learning rate的討論：

（1）在梯度下降的過程中，當我們發現loss的值很小的時候，這時我們可能以為gradident已經到了local min=0（低谷）,但是很多時候，loss很小并不是因為已經到達了低谷，而是（如下圖）：

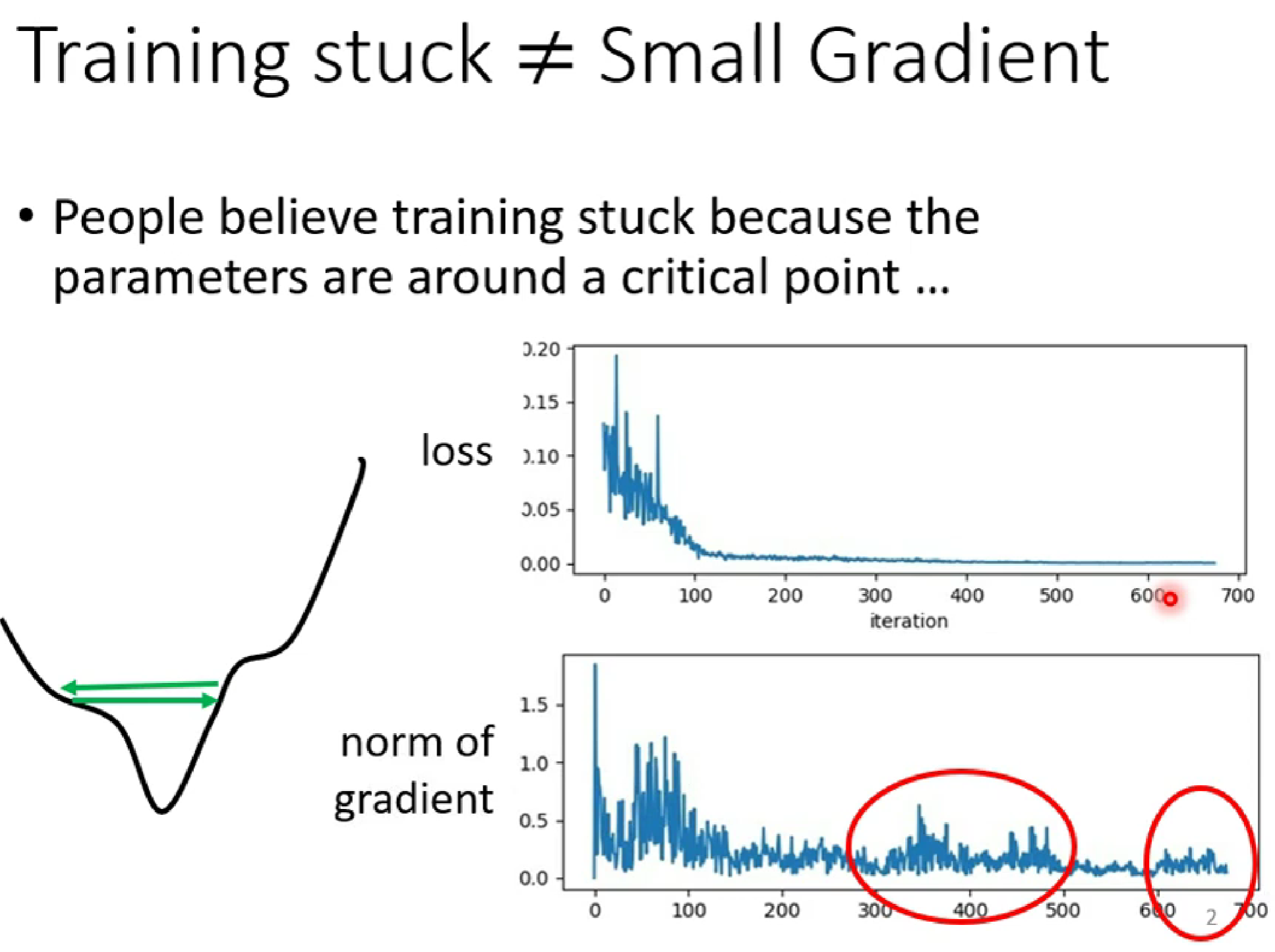
如上圖，當右上角的loss幾乎為0時，右下角的gradient并沒有趨近于0，而是出現反復的極值 ，這種情況下是因為learning rate過大，是的變化的幅度過大，是的optimisization卡在山腰（如左下角）。

---

（2）然而，我們指的learning rate并不是越大越好，也不是越小越好。

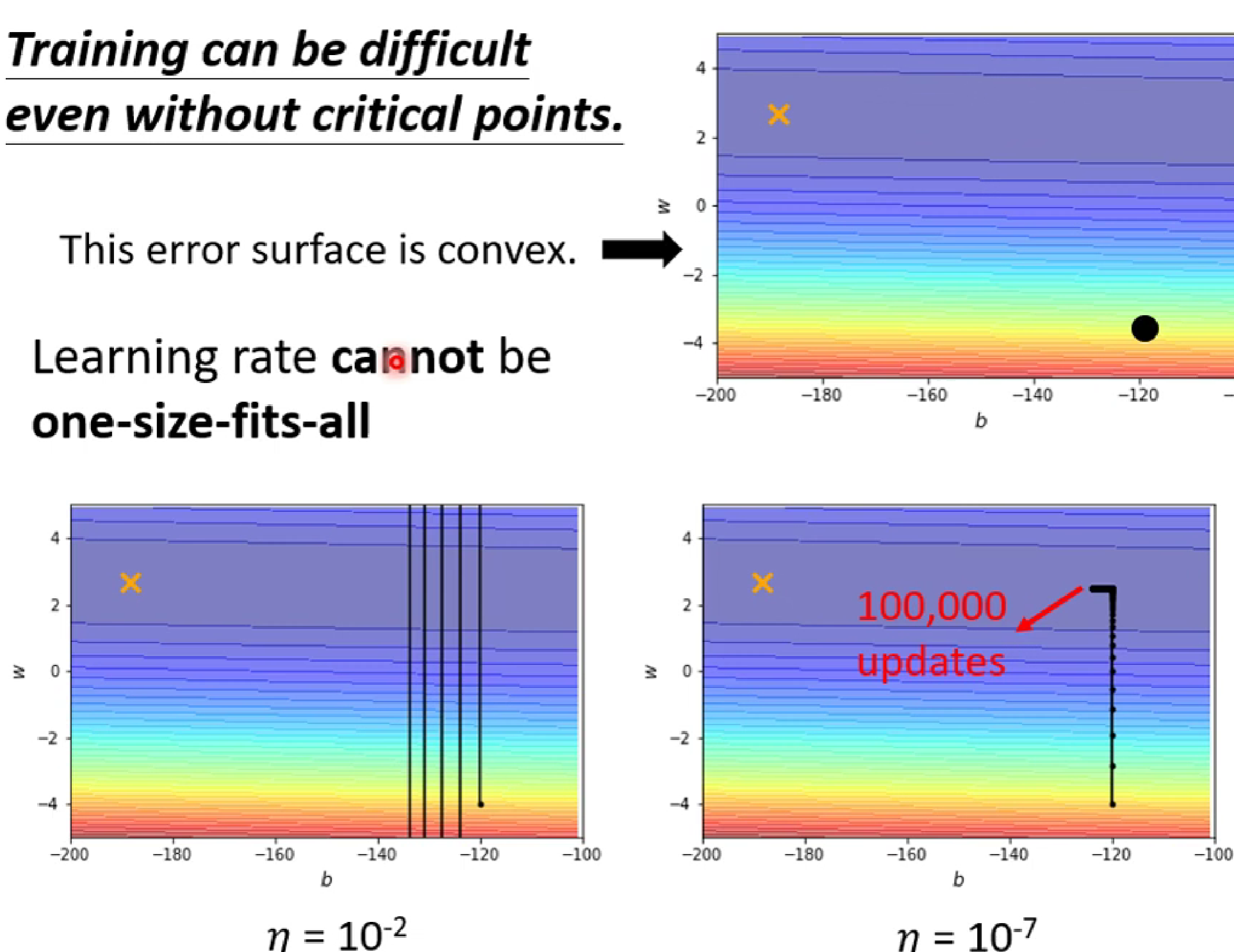
如上圖左下角，因為learning rate過大，使得梯度跨度過大不能進入低谷到達黃色叉叉，而如果選擇?learning rate過大，梯度移動緩慢，在進入低谷后在大updates之后還是難以到達黃色叉叉。

---

因為，我們需要一個自動化改變的learning rate,在坡度較陡的時候減小learning rate，在坡度較小的時候增大.

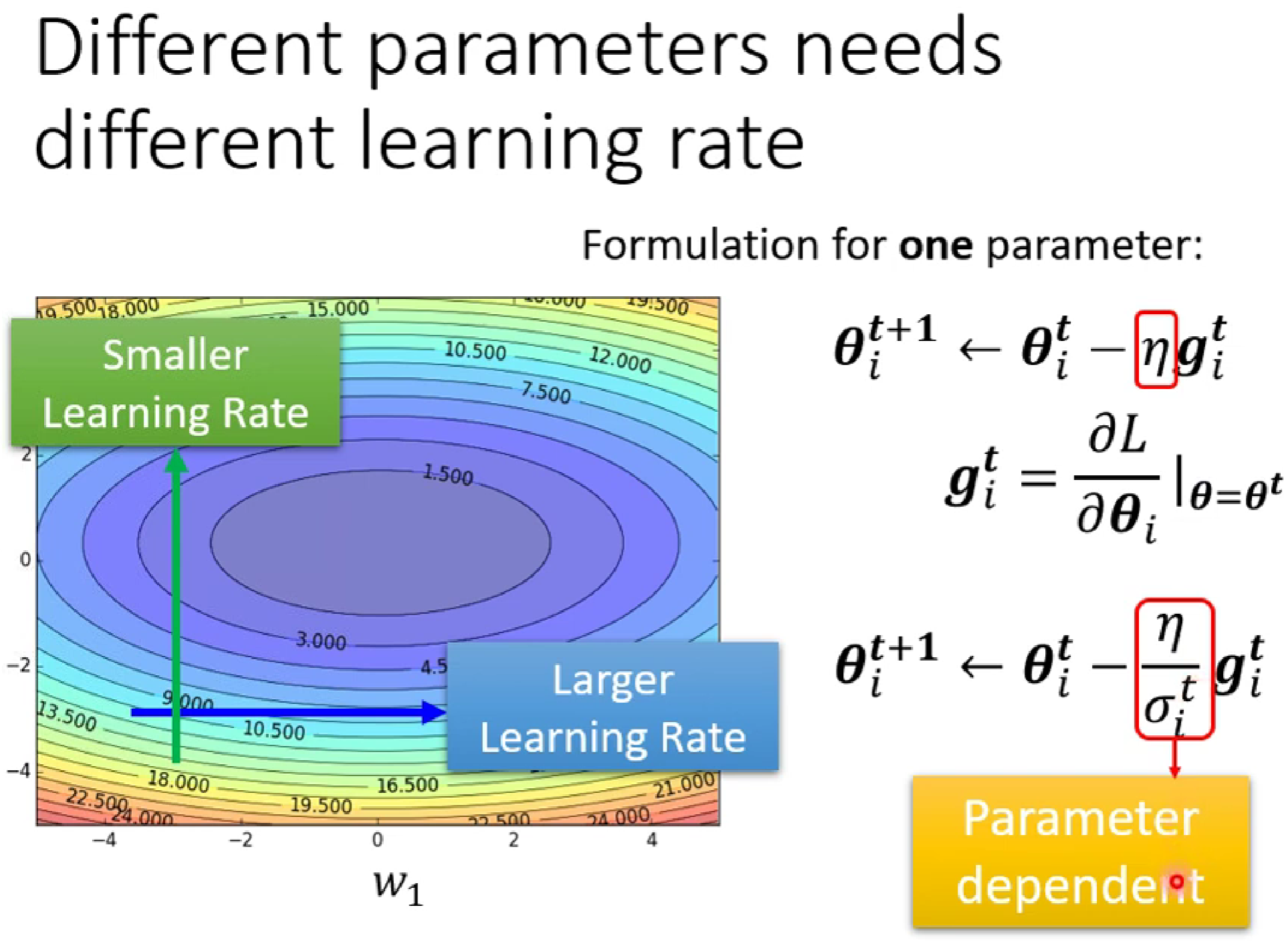
這時，我們想著在之前的learning rate 下加一個隨i變化的δ。

δ的求法如下：
（第一種求法）δ是前面所有gradient絕對值的均方

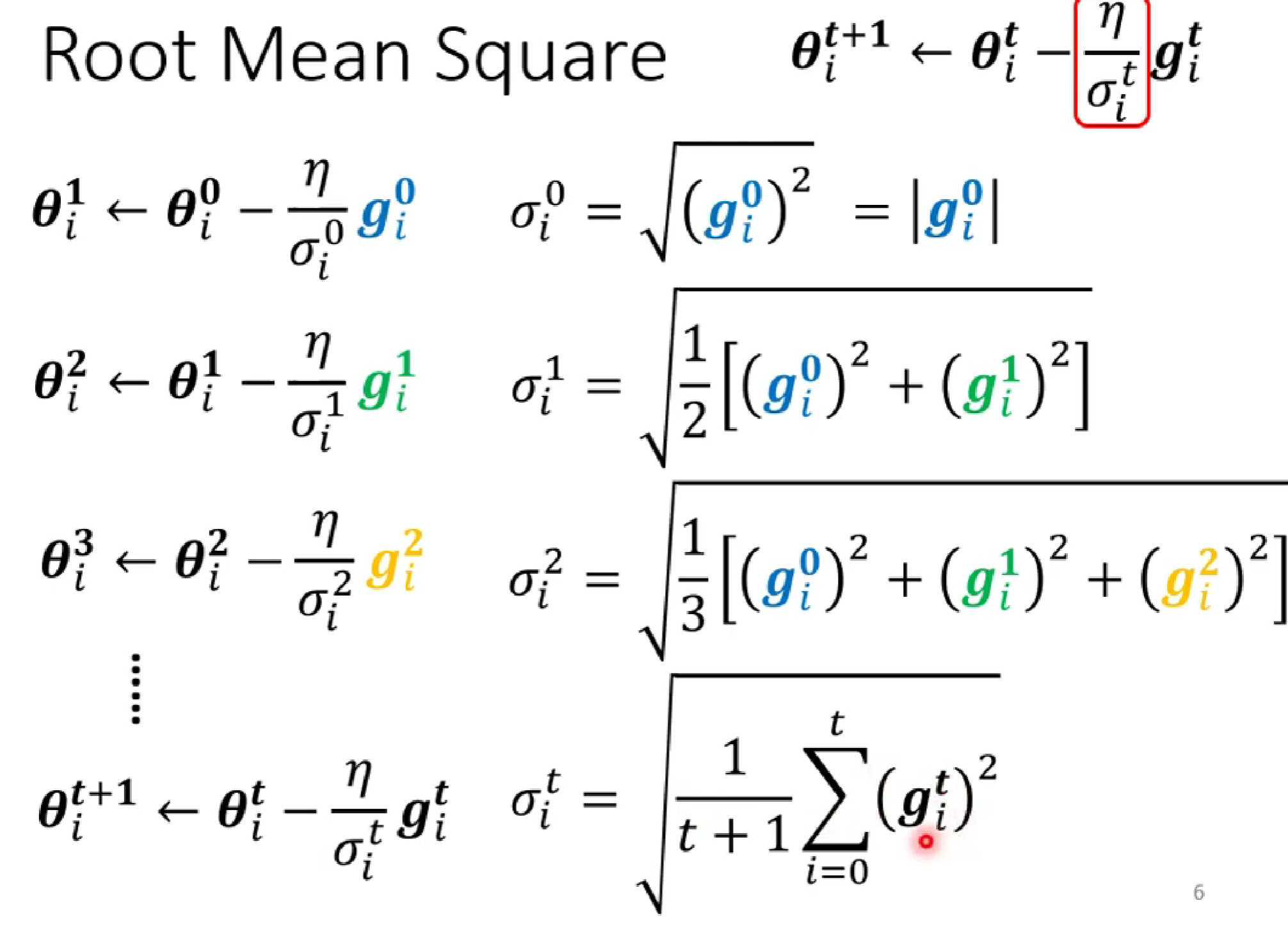
（第二種求法） ：第一種的缺點是，因為是全部平均，難以在陡的地方快速減小gradident，在緩的地方減小gradident。為此，我們添加了α權重，減少之前的梯度影響，但又保留一定的慣性。

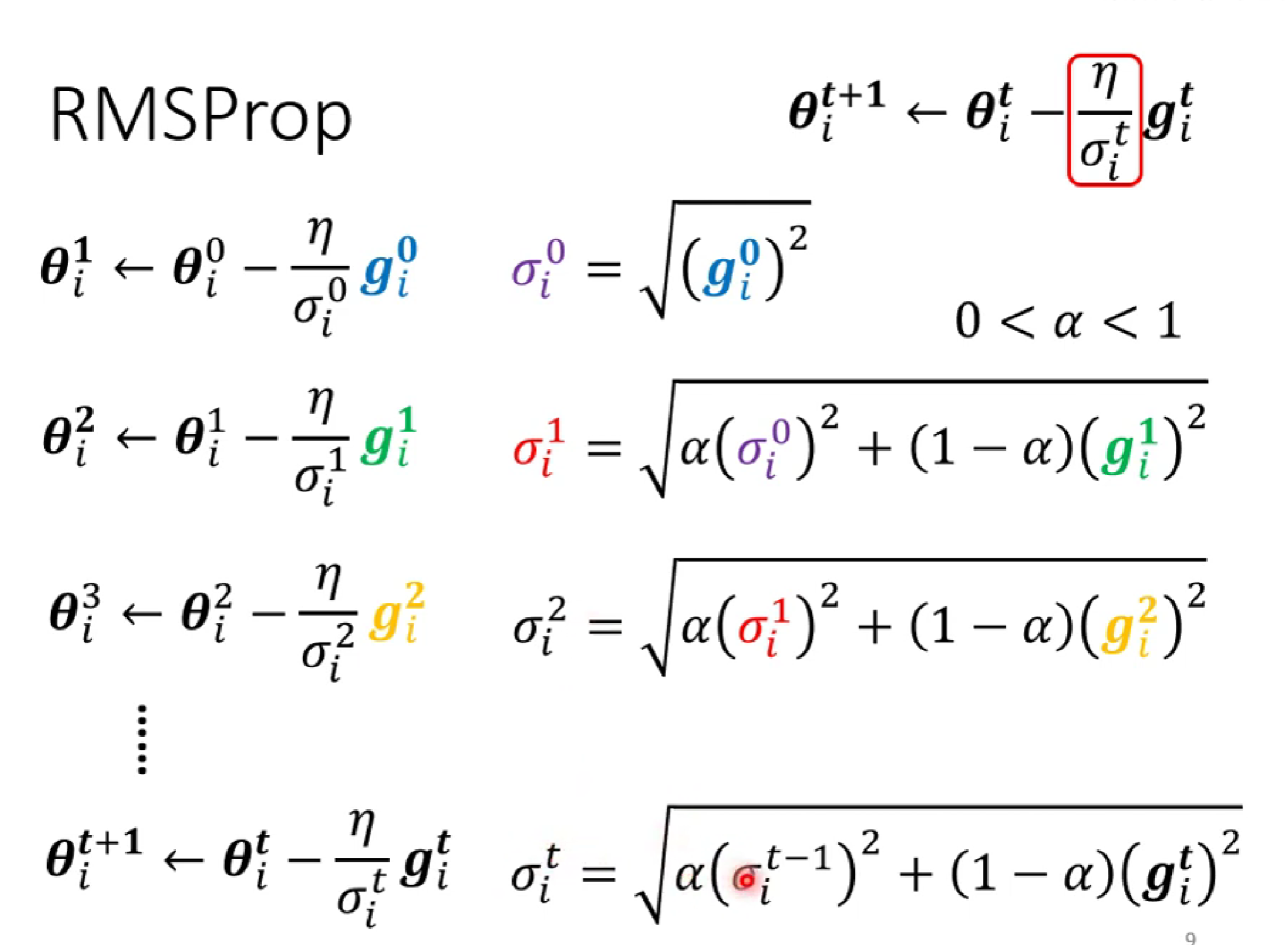
但是呢，運行后的結果會出現：

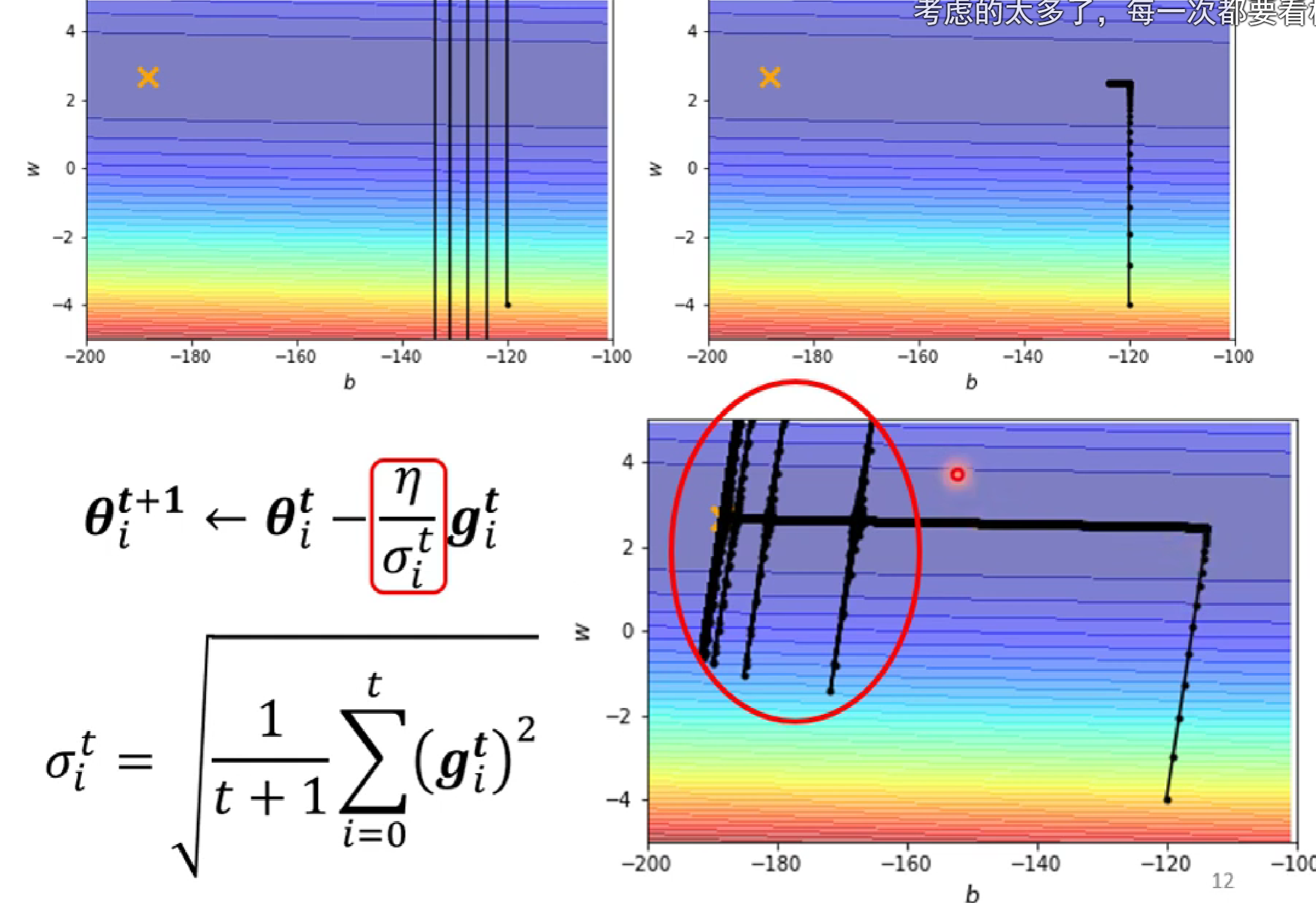
?這是因為，在y軸方向，一開始較陡，δ較大，當左轉進入較緩的低谷時，δ中的gardient不斷增大，當前面的大gradient的和影響不斷減小，由當前的δ占主導時，小δ使得y軸learning rate突然增大，發生沿y方向移動，之后由于遇上陡坡，learning rate減小而返回。

---

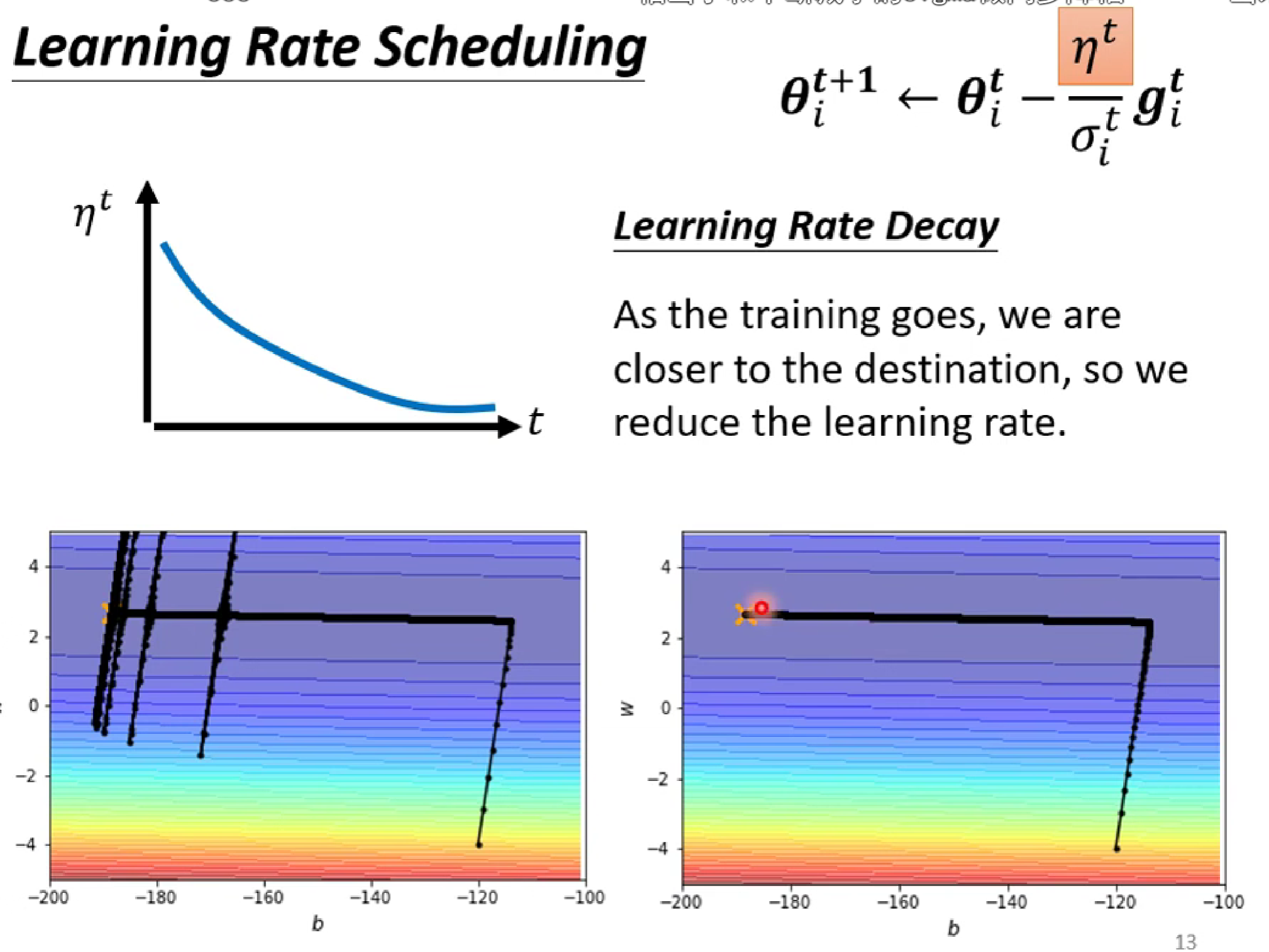
解決方法：讓learning rate n也隨著t減小（有點模擬退火的思維）

還有一個方法：進行預加熱（Warm up）。

Warmup的核心思想是在訓練的初始階段，將學習率從較小的值逐步增加到預設的目標值，而不是直接使用較大的學習率。這一過程類似于“熱身”，讓模型在訓練初期逐步適應數據分布，從而減少訓練的不穩定性。

今天就學到這啦。?