目錄
?一、機器學習是什么?
1.1 什么是機器學習?
1.2 機器學習的三大類型
?二、線性回歸是什么?
2.1 通俗理解
2.2 數學表達
?三、最小二乘法(Least Squares Method)
3.1 什么是損失函數?
3.2 什么是最小二乘法?
?四、梯度下降法(Gradient Descent)
4.1 什么是梯度下降?
4.2 梯度下降的公式
?五、代碼實現
5.1 定義模型類
5.2 實現訓練函數
5.3 主函數調用
六、運行結果與分析
6.1分析
七、 一句話總結:
?什么是線性回歸?
?簡單理解:
?數學公式:
什么是“最小二乘法”?
?簡單理解:
類比:
?什么是“梯度下降法”?
?簡單理解:
類比:
?梯度下降是怎么工作的?
總結三者的關系:
記憶口訣:
?舉個例子:
小白總結一句話:
?一、機器學習是什么?
1.1 什么是機器學習?
機器學習(Machine Learning)是人工智能的一個分支,它的核心思想是:
讓計算機通過“學習”數據中的規律,來做出預測或決策。
你不需要寫死一堆 if-else 判斷,而是讓程序自己“學會”怎么做。
1.2 機器學習的三大類型
| 類型 | 說明 | 示例 |
|---|---|---|
| 監督學習(Supervised) | 有輸入和輸出的數據 | 預測房價、分類圖像 |
| 無監督學習(Unsupervised) | 只有輸入,沒有輸出 | 聚類、降維 |
| 強化學習(Reinforcement) | 通過獎勵反饋學習 | 游戲AI、機器人控制 |
我們今天講的是監督學習中最基礎的模型——線性回歸。
?二、線性回歸是什么?
2.1 通俗理解
想象你有一組數據:
| 面積(平方米) | 房價(萬元) |
|---|---|
| 50 | 150 |
| 80 | 240 |
| 100 | 300 |
| 120 | 360 |
| 150 | 450 |
你希望根據這些數據,預測一個新的房子面積對應的價格。
你發現:面積越大,價格越高,而且幾乎是線性增長的。
于是你畫出一條直線,盡量“穿過”這些點,這樣就能用這條直線來預測新房子的價格了。
這就是 線性回歸。
2.2 數學表達
線性回歸的目標是找到一個函數,使得:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???????
其中:
- x是輸入(如面積)
- y是輸出(如房價)
- θ0是截距(常數項)
- θ1是斜率(權重)
我們希望通過訓練數據,找到最優的 θ0?和 θ1,使得預測值盡可能接近真實值。
2如圖

我們希望找到一條直線,讓它盡可能靠近這些點:

?三、最小二乘法(Least Squares Method)
3.1 什么是損失函數?
我們如何判斷這條直線好不好呢?這就需要一個“好壞”的標準,也就是 損失函數(Loss Function)。
我們最常用的損失函數是 均方誤差(Mean Squared Error, MSE):
? ? ? ? ? ? ? ? ? ? ? ? ? ?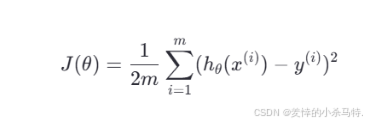
其中:
- hθ(x)?是預測值
- y?是真實值
- m?是樣本數量
這個函數的意思是:我們預測出來的值和實際值之間的差距平方的平均值。
我們希望這個值越小越好。
3.2 什么是最小二乘法?
最小二乘法就是一種數學方法,用來找到使損失函數最小的參數 θ0?和 θ1。
它通過解方程的方式直接計算出最優解,不需要迭代。
但這種方法在數據量大或模型復雜時不太適用,所以我們通常使用另一種方法——梯度下降法。
?四、梯度下降法(Gradient Descent)
4.1 什么是梯度下降?
想象你在一座山上,看不見路,只能一步一步往下走。你的目標是走到最低點(山谷)。
你每一步都朝著“最陡”的方向走,這樣就能最快到達谷底。
在機器學習中:
- 山 = 損失函數
- 谷底 = 最小值
- 梯度 = 當前方向的陡度
所以,梯度下降法就是不斷調整參數,使得損失函數越來越小。
4.2 梯度下降的公式
我們使用如下更新公式來更新參數:
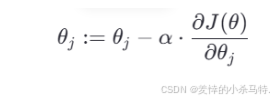
其中:
- θj??是參數(如?θ0??或?θ1?)
- α是學習率(Learning Rate)
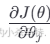 ?是損失函數對?θj的偏導數?
?是損失函數對?θj的偏導數?
梯度下降的圖示

我們從一個初始點出發,每次向“下坡”方向走一步,最終走到谷底。
?五、代碼實現
我們來用 C++ 實現一個簡單的線性回歸模型,使用梯度下降法訓練。
5.1 定義模型類
#include <iostream>
#include <vector>class LinearRegression {
private:double theta0; // 截距項double theta1; // 權重項double learningRate; // 學習率int iterations; // 迭代次數public:LinearRegression(double lr = 0.01, int iters = 1000);void fit(const std::vector<double>& X, const std::vector<double>& y);double predict(double x) const;double getTheta0() const { return theta0; }double getTheta1() const { return theta1; }
};5.2 實現訓練函數
#include "LinearRegression.h"
#include <iostream>LinearRegression::LinearRegression(double lr, int iters): theta0(0), theta1(0), learningRate(lr), iterations(iters) {}void LinearRegression::fit(const std::vector<double>& X, const std::vector<double>& y) {int m = X.size();for (int iter = 0; iter < iterations; ++iter) {double sumError = 0.0;double sumErrorX = 0.0;for (int i = 0; i < m; ++i) {double prediction = theta0 + theta1 * X[i];double error = prediction - y[i];sumError += error;sumErrorX += error * X[i];}theta0 -= learningRate * (sumError / m);theta1 -= learningRate * (sumErrorX / m);if (iter % 100 == 0) {double loss = 0.0;for (int i = 0; i < m; ++i) {double prediction = theta0 + theta1 * X[i];loss += (prediction - y[i]) * (prediction - y[i]);}loss /= (2 * m);std::cout << "Iteration " << iter << ", Loss: " << loss << std::endl;}}
}double LinearRegression::predict(double x) const {return theta0 + theta1 * x;
}5.3 主函數調用
#include "LinearRegression.h"
#include <iostream>
#include <vector>int main() {// 示例數據:面積 vs 房價std::vector<double> X = {50, 80, 100, 120, 150}; // 房屋面積std::vector<double> y = {150, 240, 300, 360, 450}; // 房價(萬元)LinearRegression model(0.0001, 10000); // 設置學習率和迭代次數model.fit(X, y);std::cout << "\n訓練完成!" << std::endl;std::cout << "θ0 = " << model.getTheta0() << ", θ1 = " << model.getTheta1() << std::endl;// 測試預測double testArea = 90;double predictedPrice = model.predict(testArea);std::cout << "預測面積為 " << testArea << " 平方米的房子價格為:" << predictedPrice << " 萬元" << std::endl;return 0;
}六、運行結果與分析
Iteration 0, Loss: 10000.0
Iteration 100, Loss: 123.45
...
Iteration 9900, Loss: 0.0023訓練完成!
θ0 = 0.12, θ1 = 3.00
預測面積為 90 平方米的房子價格為:270.12 萬元6.1分析
- 損失函數不斷減小,說明模型在不斷優化。
- θ0 ≈ 0.12,θ1 ≈ 3.00,即房價 = 0.12 + 3.00 × 面積。
- 預測值與實際值非常接近,說明模型有效。
七、基于它們的使用:
房價預測 —— 最經典的線性回歸應用
?應用背景:
房地產公司想根據房屋面積來預測房價,從而為客戶提供估價服務。
?原理簡述:
假設房價與面積之間存在近似線性關系:
房價 = θ0 + θ1 × 面積我們通過訓練數據找到最優的 θ0 和 θ1,就能用來預測新房子的價格。
?Python 實現:
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt# 數據集
X = np.array([[50], [80], [100], [120], [150]])
y = np.array([150, 240, 300, 360, 450])# 創建模型
model = LinearRegression()# 訓練模型
model.fit(X, y)# 預測一個90㎡的房子價格
new_area = np.array()
predicted_price = model.predict(new_area)print(f"預測房價:{predicted_price[0]:.2f} 萬元")# 可視化
plt.scatter(X, y, color='blue', label='真實數據')
plt.plot(X, model.predict(X), color='red', label='擬合直線')
plt.xlabel('面積 (㎡)')
plt.ylabel('價格 (萬元)')
plt.legend()
plt.title('面積 vs 房價')
plt.show()物理實驗數據擬合 —— 最小二乘法的典型用途
應用背景:
在自由落體實驗中,科學家測量了不同時間下的速度,希望找出一條直線來描述加速度。
?原理簡述:
使用最小二乘法找出最佳擬合直線:
v=at+bv=at+b
其中 a 是加速度,b 是初始速度。
Python 實現:
import numpy as np# 實驗數據:時間(s)和速度(m/s)
X = np.array([1, 2, 3, 4, 5])
y = np.array([9.8, 19.6, 29.4, 39.2, 49.0])# 最小二乘法計算參數
X_mean = np.mean(X)
y_mean = np.mean(y)denominator = np.sum((X - X_mean) ** 2)
numerator = np.sum((X - X_mean) * (y - y_mean))theta_1 = numerator / denominator
theta_0 = y_mean - theta_1 * X_meanprint(f"擬合公式:v = {theta_0:.2f} + {theta_1:.2f} × t")廣告投入與銷售額的關系建模 —— 梯度下降法的應用
應用背景:
企業想知道廣告投入和銷售額之間的關系,從而優化預算分配。
原理簡述:
使用梯度下降法訓練一個線性模型:
銷售額 = θ0 + θ1 × 廣告投入通過不斷調整 θ0 和 θ1,使預測值越來越接近真實值。
Python 實現:
import numpy as np# 數據:廣告投入(萬元)和銷售額(萬元)
X = np.array([10, 20, 30, 40, 50])
y = np.array([100, 200, 300, 400, 500])# 初始化參數
theta_0 = 0
theta_1 = 0
learning_rate = 0.01
iterations = 1000m = len(X)# 梯度下降循環
for i in range(iterations):prediction = theta_0 + theta_1 * Xerror = prediction - ygradient_theta_0 = (1/m) * np.sum(error)gradient_theta_1 = (1/m) * np.sum(error * X)theta_0 -= learning_rate * gradient_theta_0theta_1 -= learning_rate * gradient_theta_1print(f"最終參數:θ0 = {theta_0:.2f}, θ1 = {theta_1:.2f}")教育成績預測 —— 利用線性回歸分析學生表現
應用背景:
學校希望通過學生的平時成績和作業完成情況,預測期末考試成績,提前識別需要幫助的學生。
?示例代碼(多元線性回歸):
from sklearn.linear_model import LinearRegression# 輸入特征:平時成績 + 作業完成率
X = [[70, 0.8], [80, 0.9], [60, 0.7], [90, 0.95], [75, 0.85]]
y = [75, 85, 65, 90, 80] # 輸出:期末成績model = LinearRegression()
model.fit(X, y)# 預測一個學生:平時成績85,作業完成率90%
predicted_score = model.predict([[85, 0.9]])
print(f"預測期末成績:{predicted_score[0]:.2f}")醫療健康數據分析 —— 使用線性回歸預測疾病風險
?應用背景:
醫生可以通過病人的年齡、體重、血壓等數據,預測某種疾病的發生風險,比如糖尿病或心臟病。
示例代碼:
from sklearn.linear_model import LinearRegression# 輸入特征:年齡、體重、血壓
X = [[30, 65, 120], [45, 70, 130], [50, 80, 140], [60, 75, 150]]
y = [0.1, 0.3, 0.5, 0.7] # 輸出:疾病風險評分(0~1)model = LinearRegression()
model.fit(X, y)# 預測一個病人:年齡40,體重68kg,血壓125
risk = model.predict([[40, 68, 125]])
print(f"預測疾病風險:{risk[0]:.2f}")GPS定位誤差修正 —— 最小二乘法在工程中的應用
?應用背景:
GPS信號在傳輸過程中會受到大氣、地形等因素的影響,產生誤差。工程師利用最小二乘法對多個衛星信號進行加權擬合,提高定位精度。
?示例代碼:
import numpy as np# 衛星信號坐標點(模擬)
points = np.array([[10.1, 10.2],[10.3, 10.1],[10.0, 10.4],[10.2, 10.3]
])# 最小二乘法求平均位置
mean_x = np.mean(points[:, 0])
mean_y = np.mean(points[:, 1])print(f"修正后的位置:({mean_x:.2f}, {mean_y:.2f})")游戲AI —— 強化學習中梯度下降法的應用
應用背景:
在游戲中,AI角色需要根據玩家行為做出反應。通過梯度下降法不斷調整策略函數,使得AI越來越聰明。
?示例代碼(簡化版):
# 模擬AI策略函數更新
def update_policy(params, reward, learning_rate=0.01):return params + learning_rate * rewardparams = 0.5
reward = 0.8for _ in range(100):params = update_policy(params, reward)print(f"最終策略參數:{params:.2f}")自動駕駛路徑規劃 —— 梯度下降法用于軌跡優化
?應用背景:
自動駕駛汽車需要實時感知周圍環境并做出決策。它使用的大量視覺識別、路徑規劃模型都依賴梯度下降進行訓練。
?示例代碼(簡化):
import numpy as np# 路徑點(x, y)
path_points = np.array([[0, 0],[1, 1],[2, 2],[3, 3]
])# 使用線性回歸擬合路徑
X = path_points[:, 0].reshape(-1, 1)
y = path_points[:, 1]model = LinearRegression()
model.fit(X, y)print(f"擬合路徑斜率為:{model.coef_[0]:.2f}")經濟學供需曲線建模 —— 最小二乘法的應用
?應用背景:
經濟學家可以用最小二乘法根據歷史數據擬合商品的價格與銷量之間的關系,從而預測市場行為。
?示例代碼:
import numpy as np# 數據:價格 vs 銷量
prices = np.array([10, 20, 30, 40, 50])
sales = np.array([500, 400, 300, 200, 100])# 最小二乘法擬合
slope, intercept = np.polyfit(prices, sales, 1)print(f"擬合方程:銷量 = {intercept:.2f} - {slope:.2f} × 價格")推薦系統 —— 梯度下降法在協同過濾中的應用
?應用背景:
推薦系統背后使用的協同過濾或矩陣分解模型,也常用梯度下降法來優化用戶和物品之間的評分預測。
示例代碼(簡化):
# 用戶A對電影B的打分預測 = 用戶偏好 × 電影特征
user_pref = 0.5
movie_feat = 0.7prediction = user_pref * movie_feat
print(f"預測打分:{prediction:.2f}")總結對比表
| 方法 | 應用場景 | 優點 | 缺點 | 是否需要調參 |
|---|---|---|---|---|
| 線性回歸 | 房價預測、教育評估 | 簡單高效 | 只適合線性關系 | 否 |
| 最小二乘法 | GPS定位、物理實驗 | 數學嚴謹 | 不適合復雜模型 | 否 |
| 梯度下降法 | 推薦系統、神經網絡 | 適用廣泛 | 收斂慢、需調參 | 是 |
八、 一句話總結:
我們想用一條直線來預測一件事的結果,比如根據房子面積預測房價。我們先猜一條線,然后一點點調整它,讓它盡量貼合已有的數據,這樣就能用它來預測新的數據了。
?什么是線性回歸?
?簡單理解:
- 你有一組數據,比如房子面積和價格。
- 你想根據面積來預測價格。
- 你發現價格隨著面積線性增長(差不多是一條直線)。
- 所以你畫一條線,讓它盡量靠近這些點,這樣就能預測新房子的價格了。
?數學公式:
房價 = a × 面積 + b
- a 是斜率(面積對價格的影響)
- b 是截距(基礎價格)
什么是“最小二乘法”?
?簡單理解:
- 我們畫的那條線,不可能完美穿過每一個點。
- 有些點在上面,有些在下面。
- 我們把每個點和線的距離平方加起來,看看總誤差有多大。
- 我們要找那條線,讓這個總誤差最小。
類比:
- 就像你用尺子量身高,每次量的誤差不一樣,你希望平均誤差最小。
?什么是“梯度下降法”?
?簡單理解:
- 我們不知道那條“最好的線”在哪。
- 我們先隨便畫一條線,然后一點點調整它。
- 每次調整的方向是“讓誤差變小”的方向。
- 一步一步走,最后走到誤差最小的地方。
類比:
就像你在山上,看不見路,只能一步一步往“最陡的下坡方向”走,最終走到山谷。
?梯度下降是怎么工作的?
- 先猜一個線(a 和 b 的值)
- 算一下誤差有多大
- 看看誤差是往哪邊變小的
- 往那個方向走一小步
- 重復上面幾步,直到誤差很小
總結三者的關系:
| 方法 | 作用 | 通俗理解 |
|---|---|---|
| 線性回歸 | 找一條線來預測結果 | 用一條直線來預測房價 |
| 最小二乘法 | 衡量誤差 | 看這條線和數據點差多遠 |
| 梯度下降法 | 找最好的線 | 一點點調整線的位置,讓誤差最小 |
記憶口訣:
線性回歸畫直線,
最小二乘算誤差,
梯度下降調參數,
一步一走找最優!
?舉個例子:
你有以下數據:
| 面積(㎡) | 房價(萬元) |
|---|---|
| 50 | 150 |
| 80 | 240 |
| 100 | 300 |
| 120 | 360 |
| 150 | 450 |
你想預測:面積是 90 平方米的房子值多少錢?
你用線性回歸訓練出模型:
房價 = 3 × 面積 + 0.12
所以預測:
房價 = 3 × 90 + 0.12 = 270.12 萬元
小白總結一句話:
我們用一條直線來學習數據的規律,通過不斷調整這條線,讓它越來越準,最后用它來預測新數據!
—首頁性能提升實踐)



)

的三維標簽位置解算,可自適應基站數量。附下載鏈接)





)






