
本文給出自適應錨點(基站)的Taylor算法解算TOA(到達時間)的MATLAB代碼。參考論文:《基于Taylor-Chan算法的改進UWB室內三維定位方法》中的Taylor算法來解算TOA的復現程序(MATLAB)。
文章目錄
- 運行結果
- 程序介紹
- 📊 結果輸出
- MATLAB源代碼
運行結果
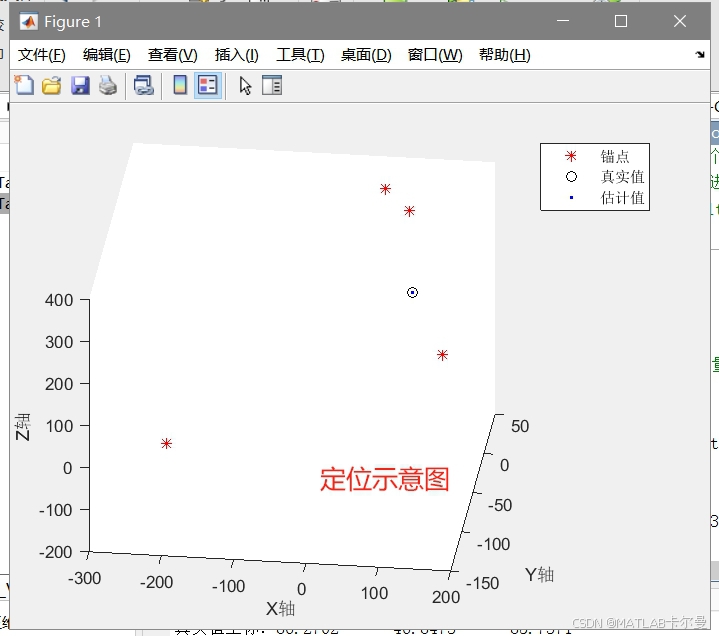
以下為定位結果示意圖:
誤差輸出(命令行截圖):
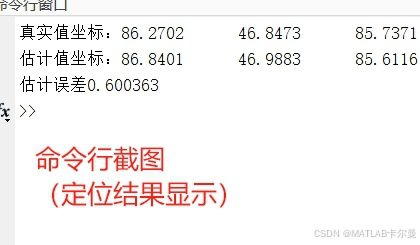
程序介紹
本程序基于 Taylor 迭代算法,實現了對三維空間的 TOA(Time of Arrival)定位解算,程序可自適應錨點數量,可自行設置3~無窮個錨點(基站),給出了精度評估、誤差可視化與迭代過程分析。
📊 結果輸出
- 每個點定位誤差(最后一個點)
- 所有點定位 RMSE:RMSE=1N∑i=1N∥p^i?pi∥2\text{RMSE} = \sqrt{\frac{1}{N} \sum_{i=1}^N \| \hat{\mathbf{p}}_i - \mathbf{p}_i \|^2}RMSE=N1?∑i=1N?∥p^?i??pi?∥2?
- 迭代誤差收斂曲線
MATLAB源代碼
程序結構如下:

部分代碼如下:
% Taylor方法解算TOA,定位三維目標、N個錨點
% 參考文獻:《基于Taylor-Chan算法的改進UWB室內三維定位方法》
% 2025-07-05/Ver1
%% 初始化與
clc;clear;close all;
rng(0);
% 定義參數和待測點位置
num_stations = 40; % 基站數量(錨點數量)
std_var1 = 1e-9; %TOA時間誤差(標準差)
% 固定基站位置
stations_position = 100*randn(num_stations,3);
c = 3e8;
% 生成待定位點坐標
position = 50*ones(1,3)+50*randn(1,3);
%% TOA 建模
delta = ones(num_stations,1)*position - stations_position; %未知點與各基站之間的相對位置(矢量)
r_ideal = (sum(delta.^2,2)).^(1/2);
完整代碼見專欄文章:【MATLAB代碼】Taylor算法用于TOA(到達時間)的三維標簽位置解算,可自適應基站數量。附matlab代碼,訂閱專欄后可查看
或單個程序的下載鏈接:https://download.csdn.net/download/callmeup/91369401
如需幫助,或有導航、定位濾波相關的代碼定制需求,請點擊下方卡片聯系作者





)









)



