參考這位大佬：https://zhuanlan.zhihu.com/p/458000359

一.?基本的投影模型

正如上面所說，相機是一個將三維物體投影為二維圖像的設備。

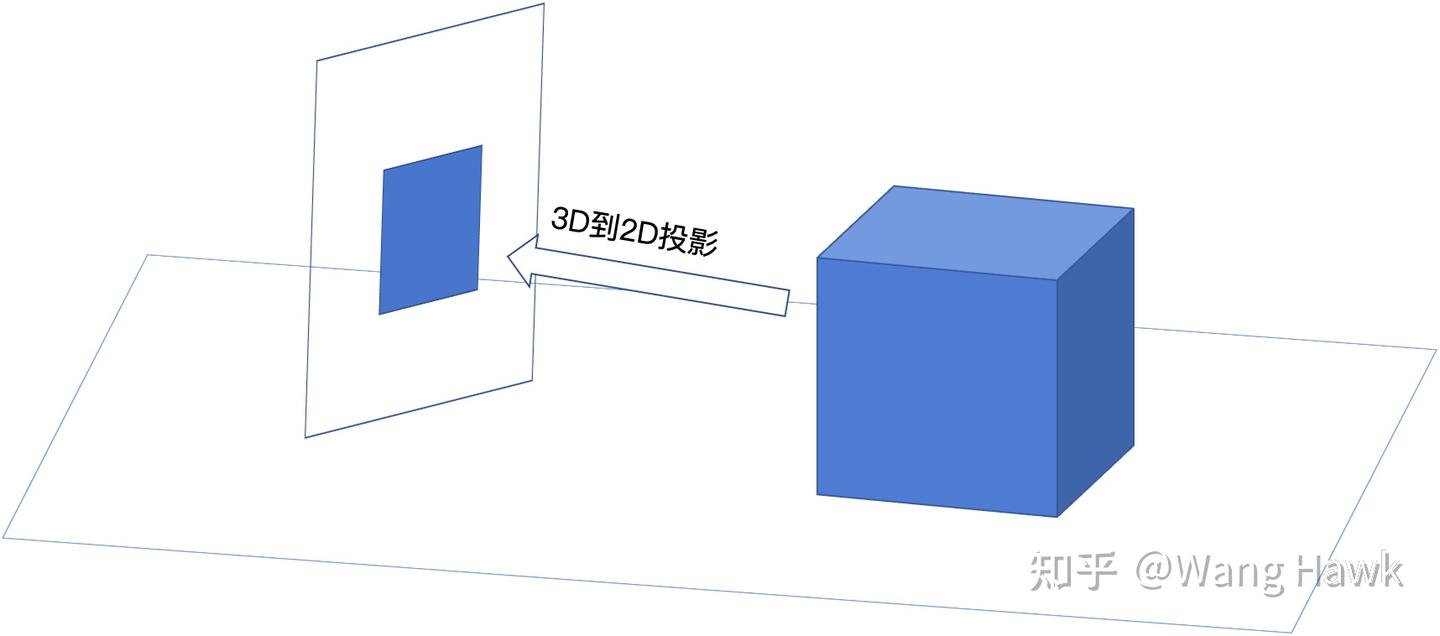
對于小孔相機，或者薄透鏡相機來說，基礎投影的數學模型可以表達為

我們把這個過程表達在笛卡爾坐標系中，是這樣的：

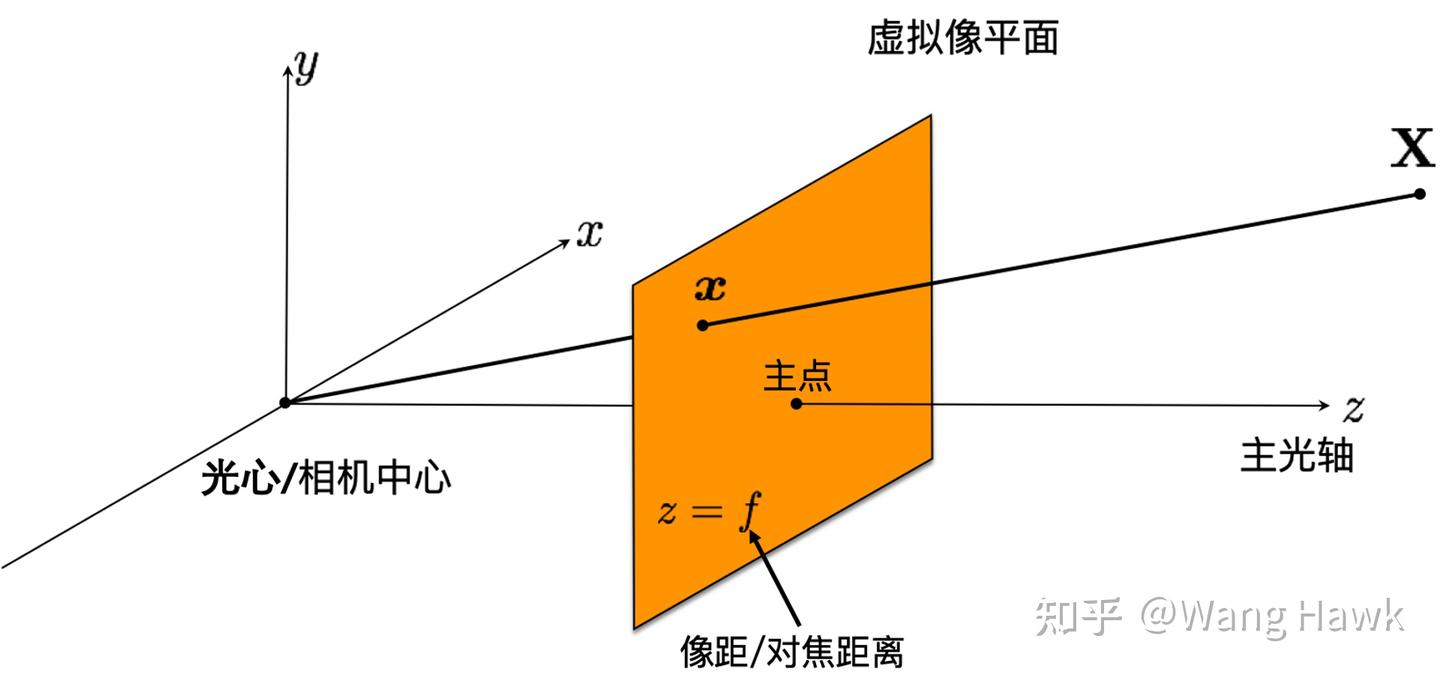
對這個模型，有幾個點需要注意：

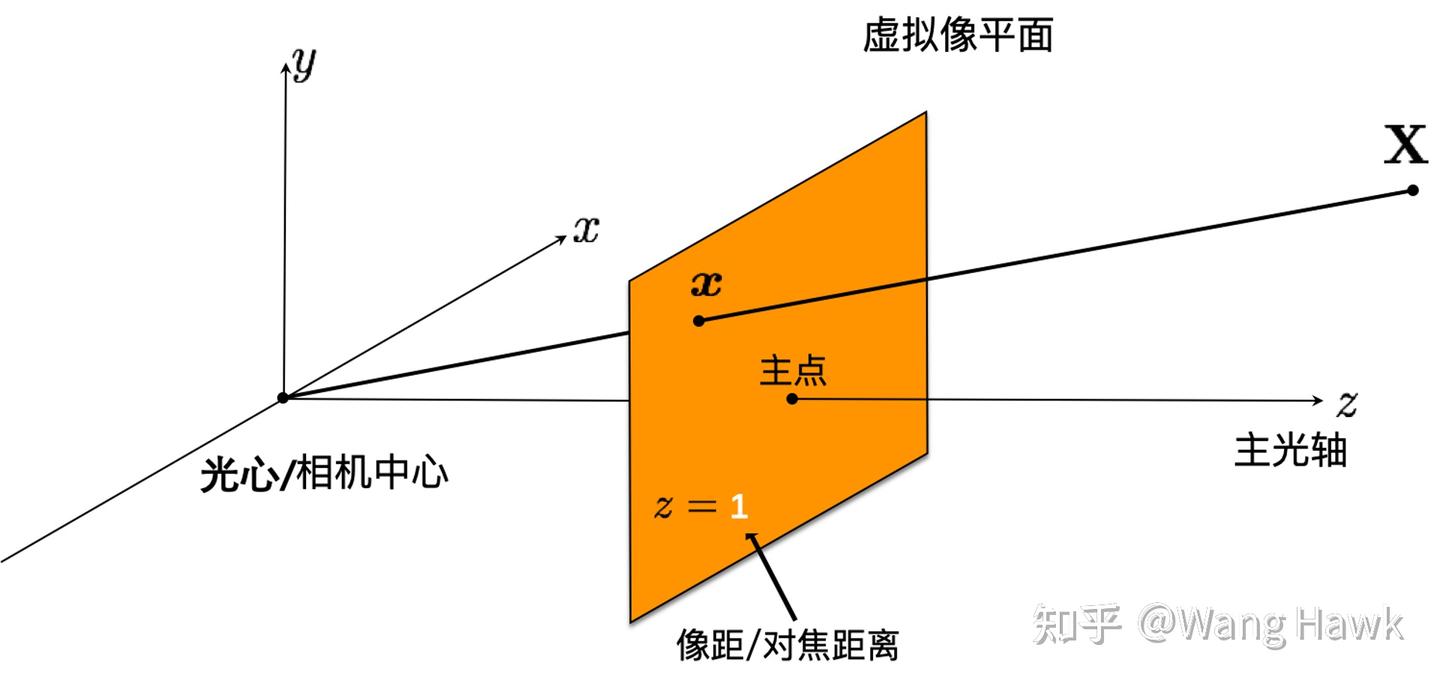
第1， 為了數學計算的方便，將像平面移到了相機之前，如下圖所示

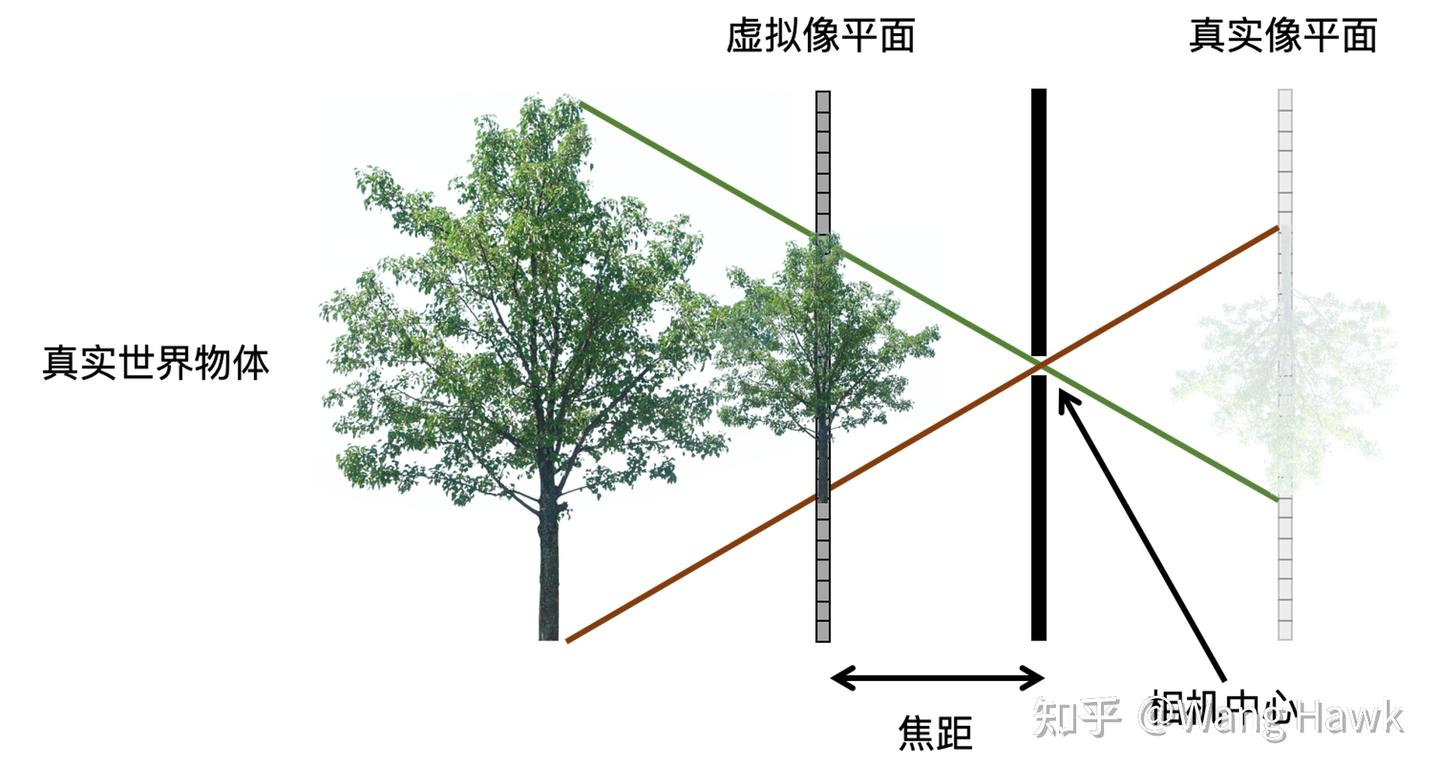
第2，薄透鏡成像模型中，假設了對焦距離和對應小孔相機的焦距一致

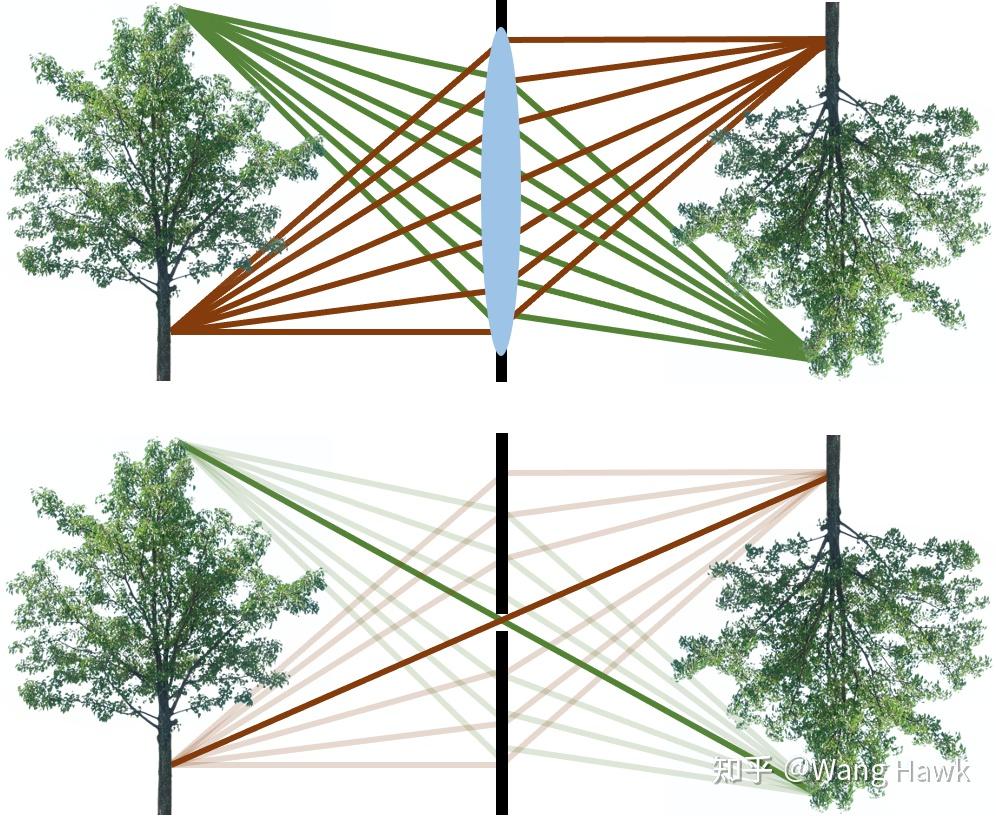
你在文獻里面可能經常會看到focal length， focus distance等等概念，有時候會比較讓人混淆。這里需要說明薄透鏡成像模型的一些假設：

1. 薄透鏡成像時，通常只考慮了接近光軸的光線
2. 薄透鏡成像時，假設像距和對應的小孔相機的焦距一致
3. 我們上圖中的f，是指對焦距離，即清晰成像的像距（傳感器到鏡頭間的距離）。而并非透鏡的焦距。

第3，這里采用了齊次坐標

現在我們來談談點的坐標變換，以及齊次坐標，稍微補充一下這些知識，更有助于理解后面的內容。

二. 變換和齊次坐標

2.1 二維變換和齊次坐標表達

先來看看二維空間中的點，我們通常用一個二維向量來表示這個一個普通二維點p，一幅圖像會由很多個二維點構成，如下圖所示。

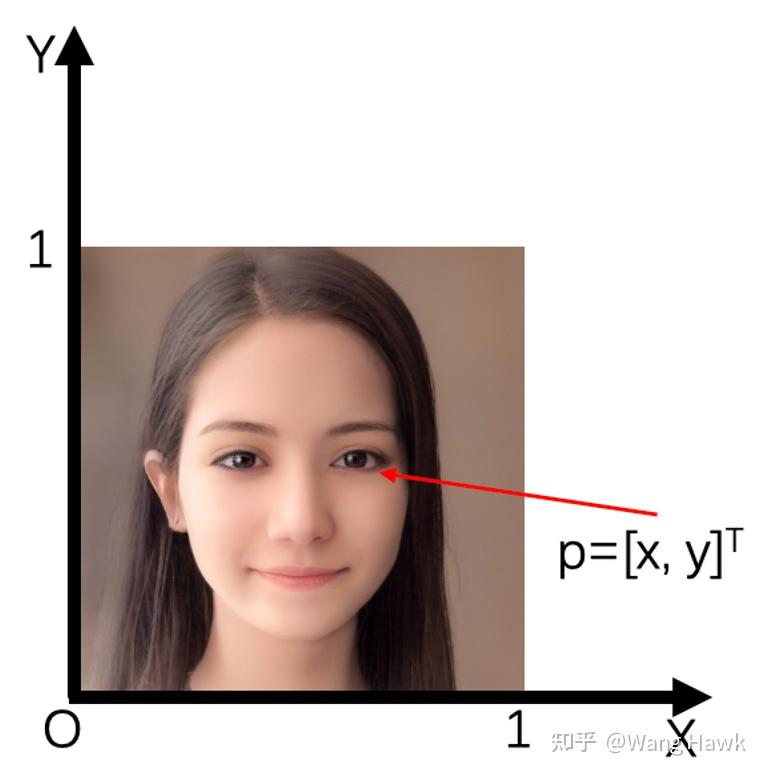
我們很容易用二維矩陣和點的乘法來表示對點（進而對圖像）的縮放、旋轉、錯切等操作，如下圖所示

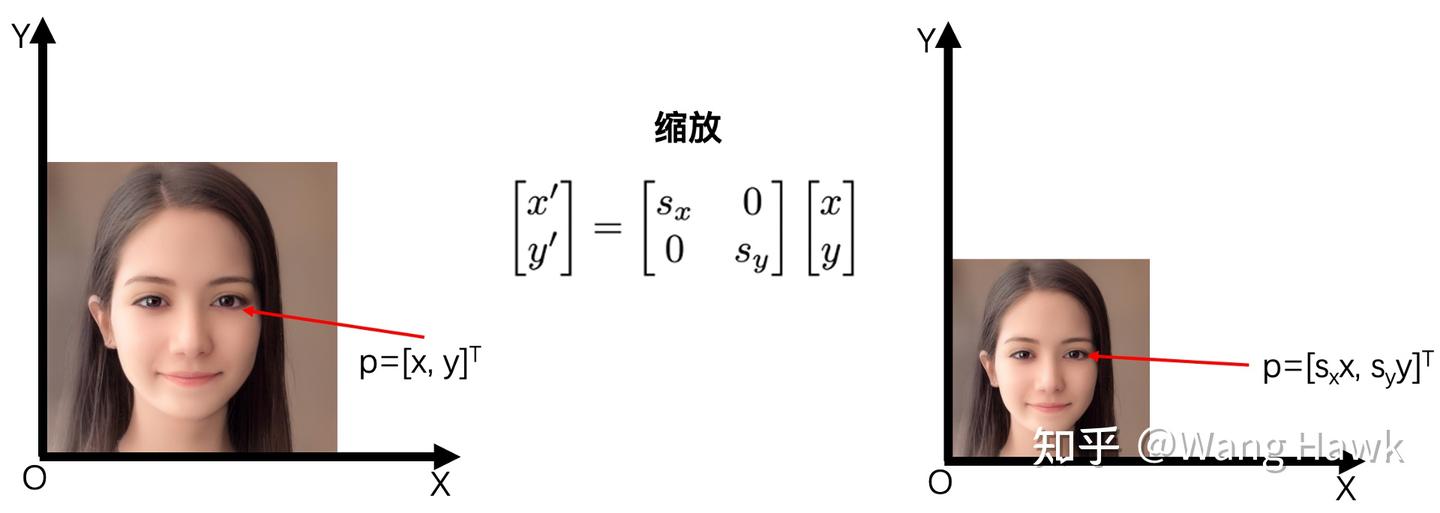
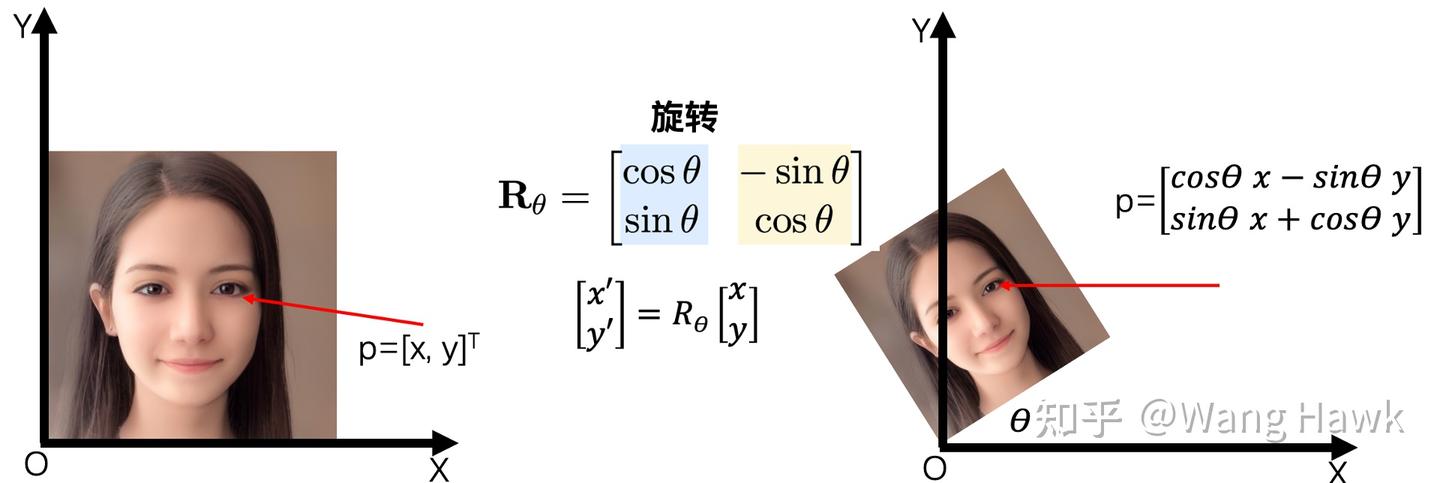
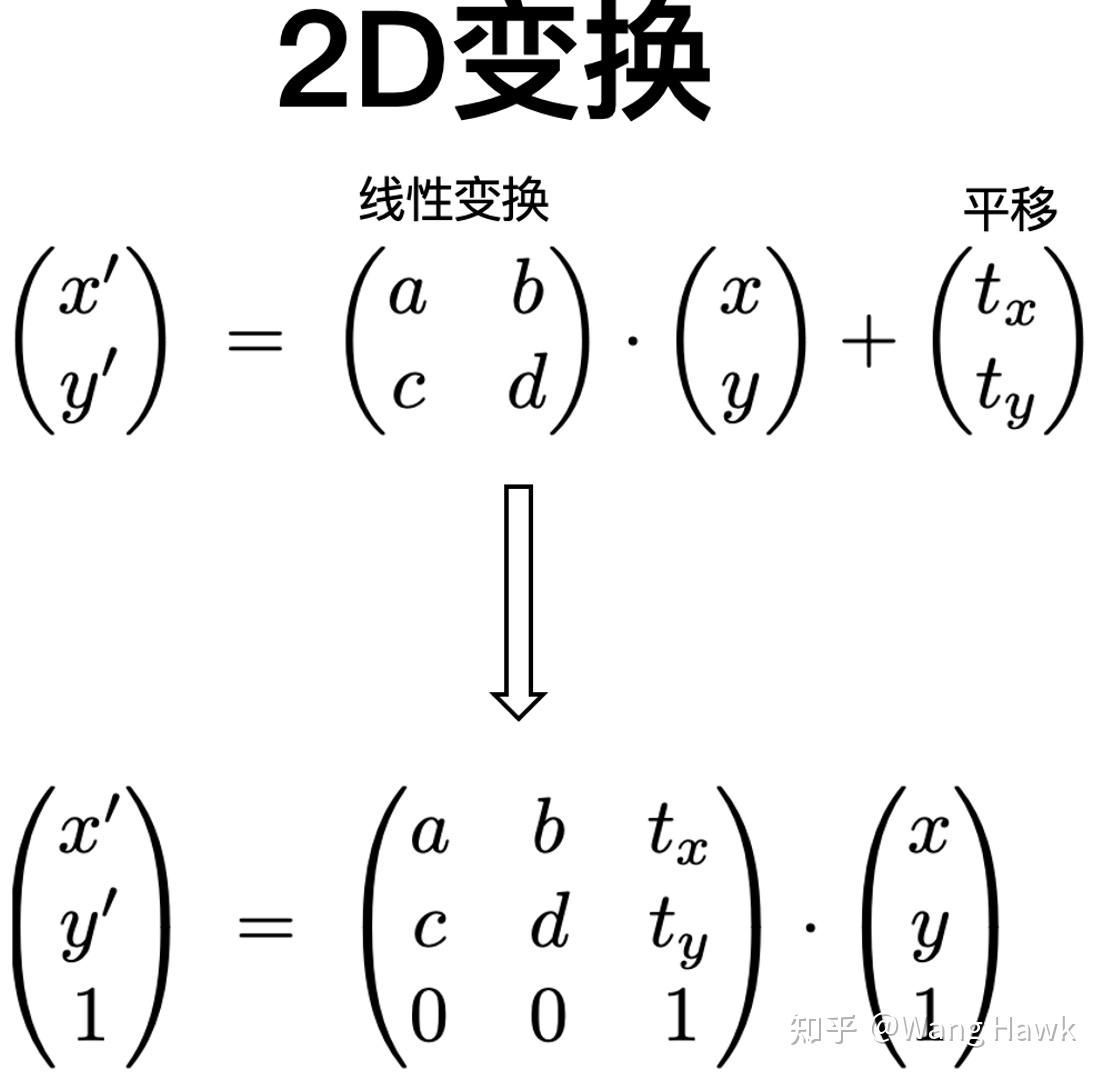
不幸的是，用二維矩陣與點的乘法無法表達二維點的平移操作。你可以自己演算下，看看下圖中是否能夠找到合理的二維矩陣和點的乘法來表達平移。

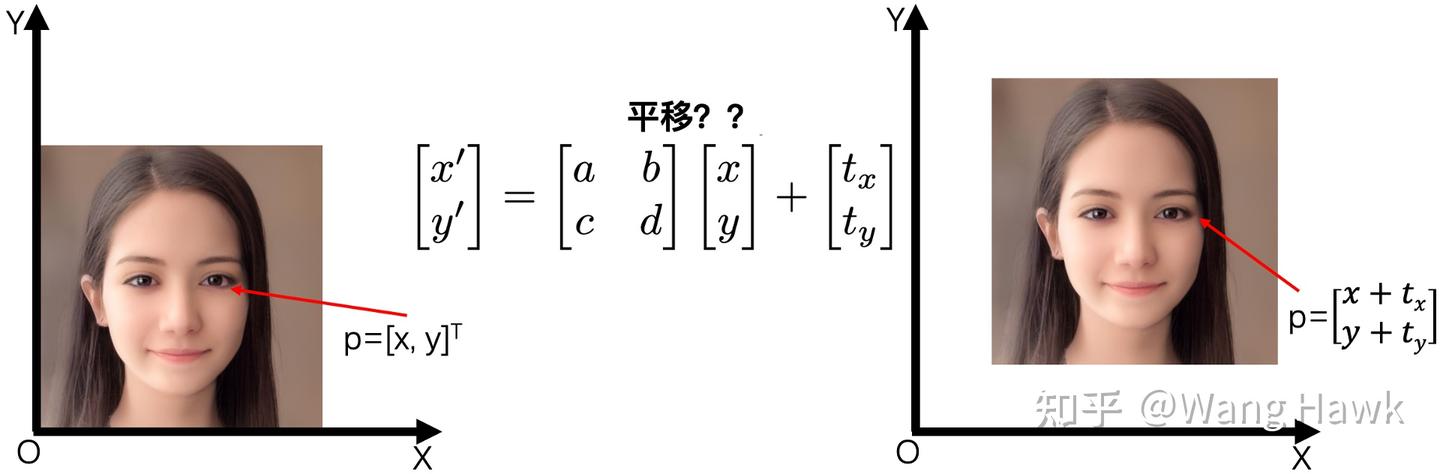
現在讓我們引入齊次坐標。當我們用齊次坐標表達一個點時，我們只需要加入一個不為0的第三個坐標，就很容易用1個三維矩陣來表達平移了。要注意的是，加入任何不為0的w后，以齊次坐標的規則按下圖進行坐標的等比例變化，都表示的是同一個點。

采用齊次坐標，我們很容易將各種二維變換統一到一起，用矩陣來表達這種變換：

2.2 三維變換和齊次坐標表達

在討論相機成像時，我們需要處理三維空間中的點。因此我們來看看三維點的齊次坐標和相關的變換。

三維點的齊次表達是二維點的齊次表達的自然衍生，依然是加入1個不為0的新維度

一些基本變換用齊次坐標的表達的形式也非常相似，這里面唯一不同的是3D旋轉

三維空間中的旋轉有可能是繞著任何一個旋轉軸進行的，形式比較復雜。我們可以先看看繞著基本的坐標軸旋轉的情況：

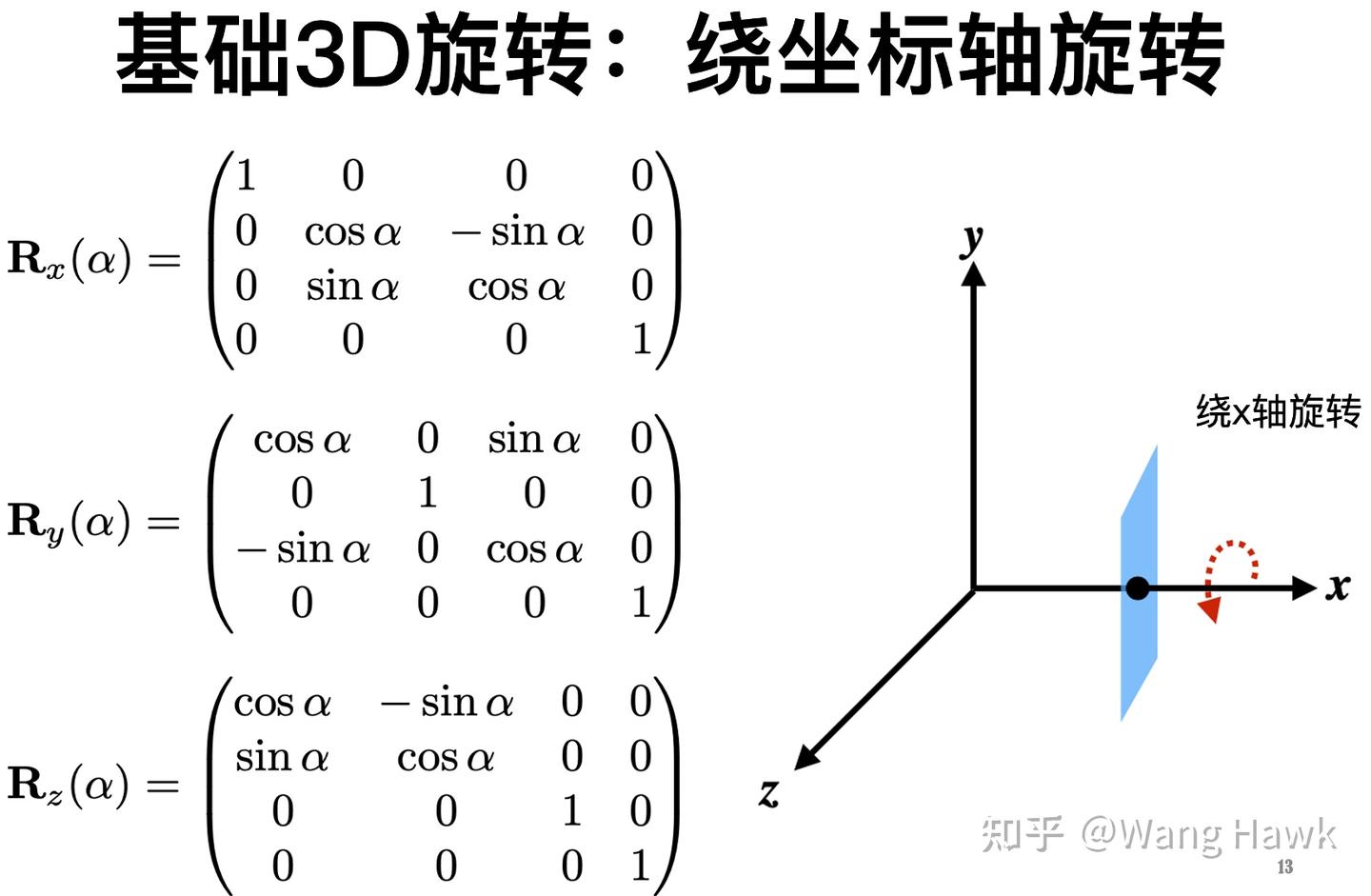
這樣，繞著任何一個旋轉軸的旋轉，可以用上面這些基礎旋轉組合而成(絕大多數情況下是)

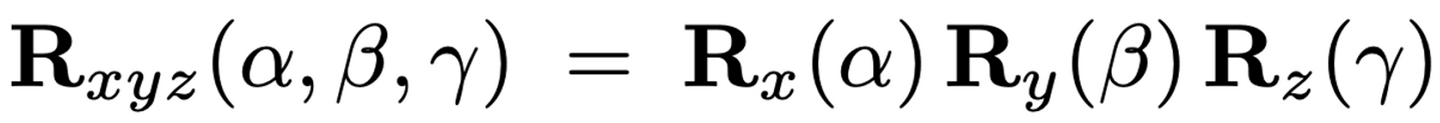
由于上面這些基礎旋轉都可以用4x4的變換矩陣表達，因此合并的旋轉矩陣也就是1個4x4的矩陣。

最終，采用了齊次坐標，我們就可以把各種三維變換也用矩陣和點的乘法來表達了：

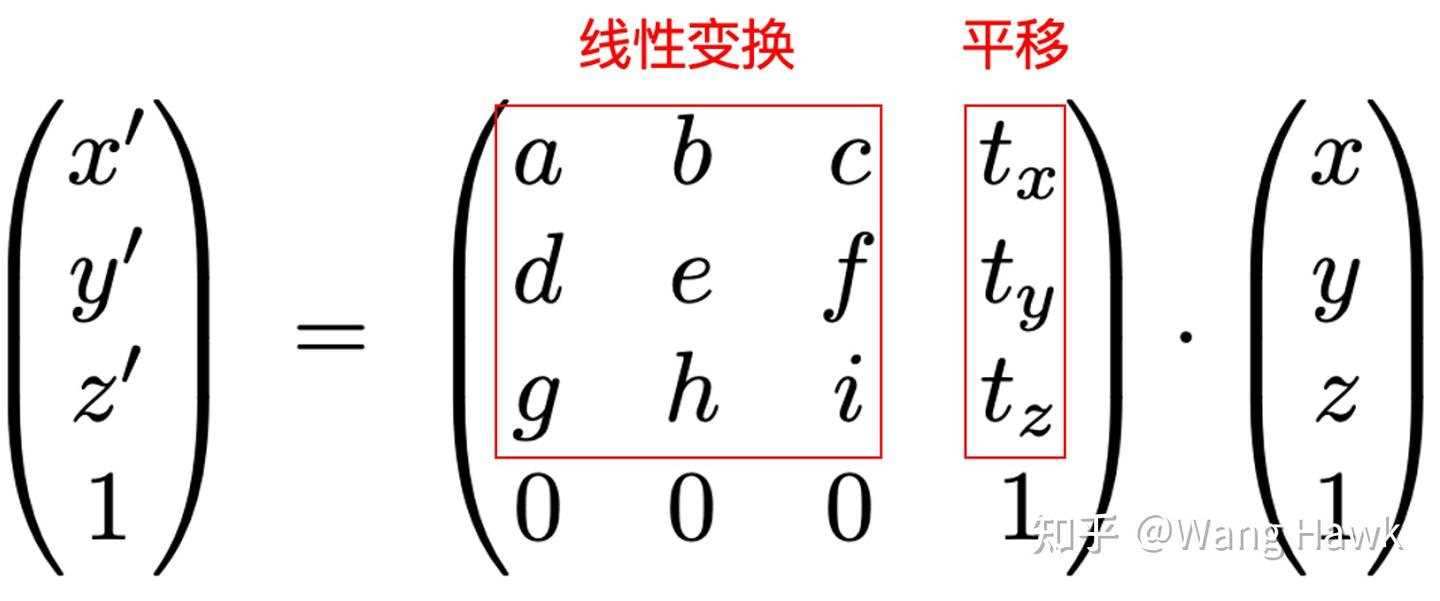
2.3 旋轉矩陣的特別之處

看看下面這張圖，我們把原圖進行旋轉?θ?度，再把結果旋轉?θ?度。

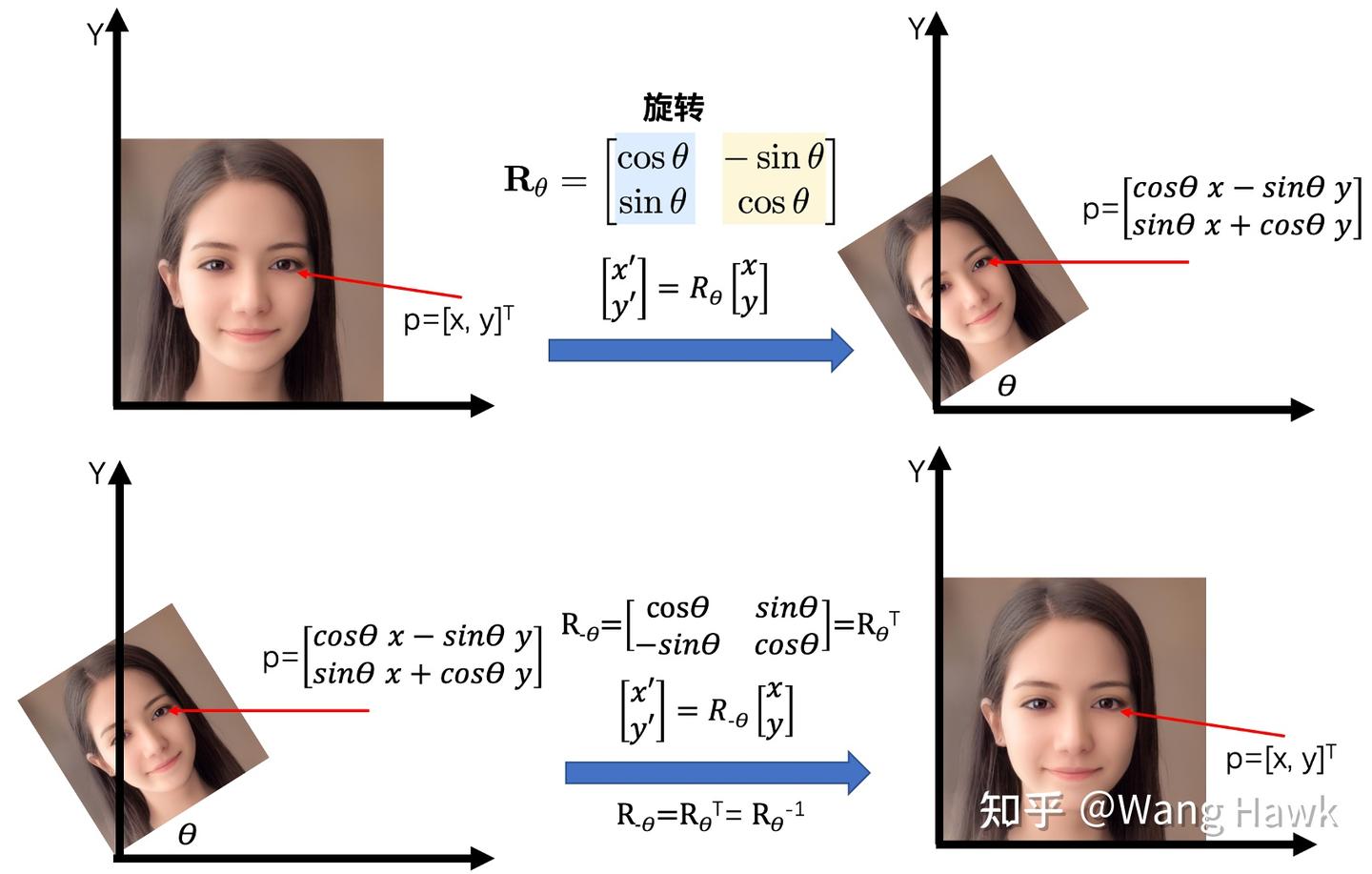
很容易得到下面兩個結論，這說明旋轉矩陣是單位正交矩陣，這個性質對之后我們理解相機矩陣是很有用的。

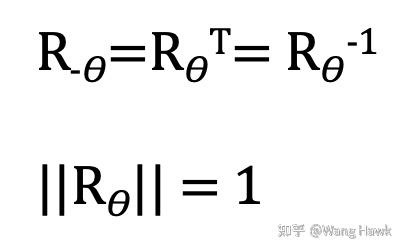
基本上，理解投影和相機矩陣的基礎數學知識就回顧到這里，差不多夠了。下一節我們繼續來看看投影和相機矩陣。

三. 投影及相機矩陣

3.1 基礎小孔相機投影矩陣

回到我們的小孔成像模型，如下圖所示。我們的問題是空間點X和虛擬像平面上的點x之間的投影矩陣是什么？

很明顯這里可以利用相似三角形來求解這個關系

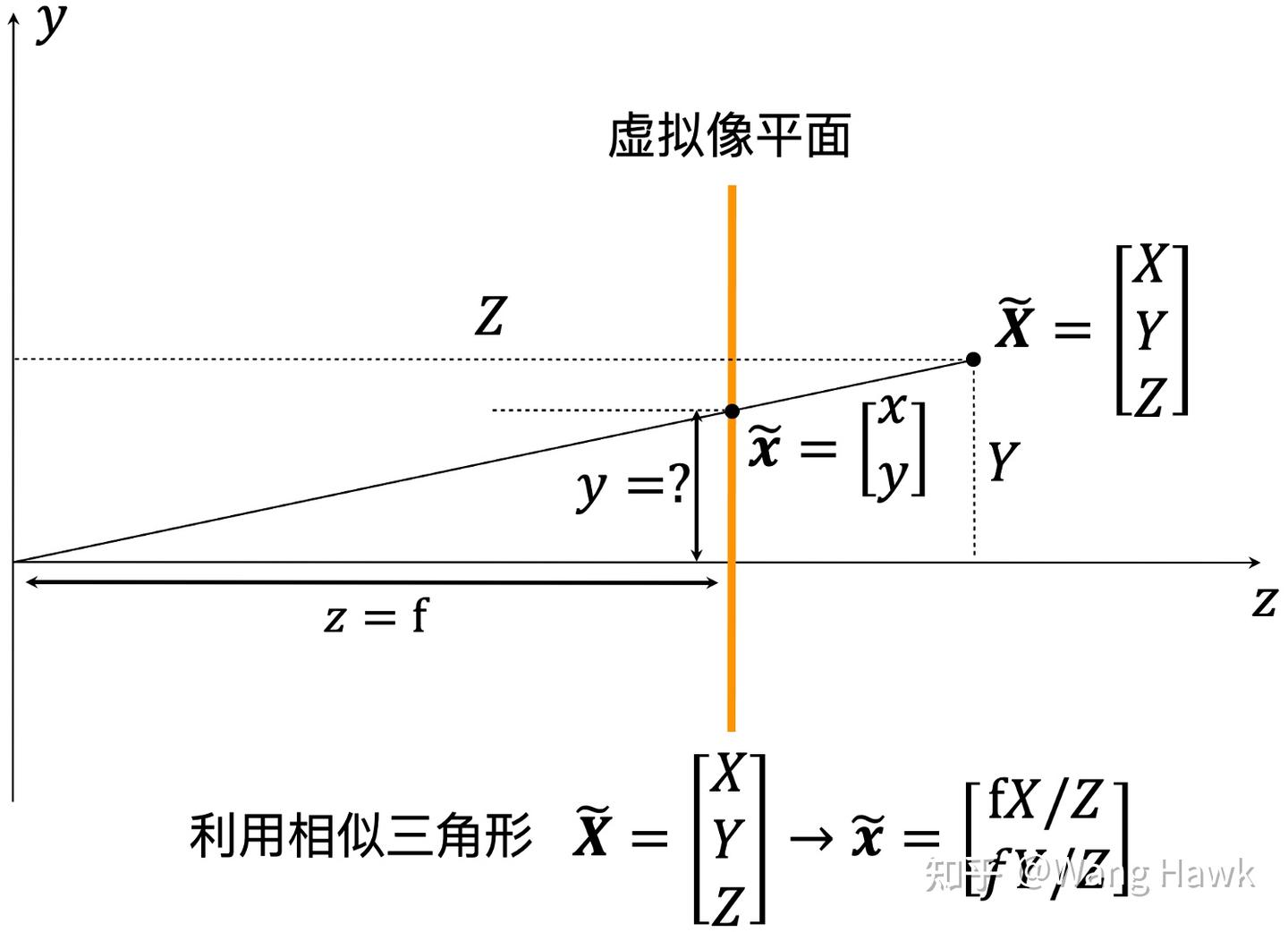
我們用齊次坐標來表達這個過程，注意點的二維齊次坐標的特性是任意等比例變換后，表示的是同一個點。

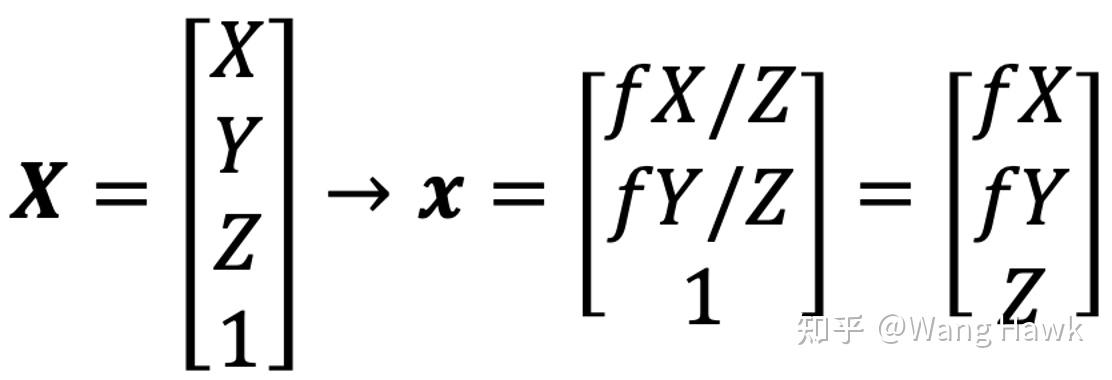
稍微思考一下，就可以用矩陣和點的乘法來表達，這里轉換矩陣就是P

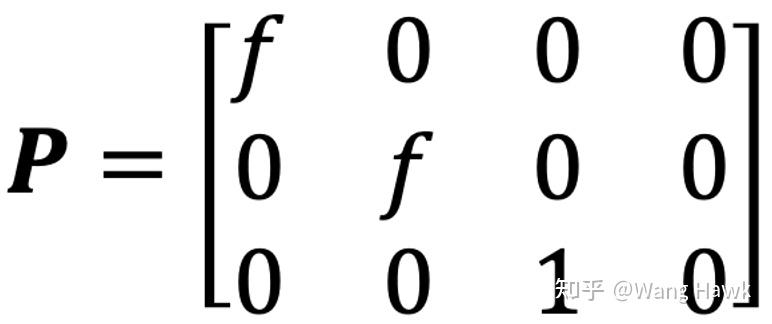
這個轉換矩陣還可以進一步拆分成下面的樣子：

這里面的歸一化投影變換，可以按下圖來理解，即將三維空間點投影到了一個對焦距離為1的標準像平面上。

3.2 從投影圖像到像素坐標

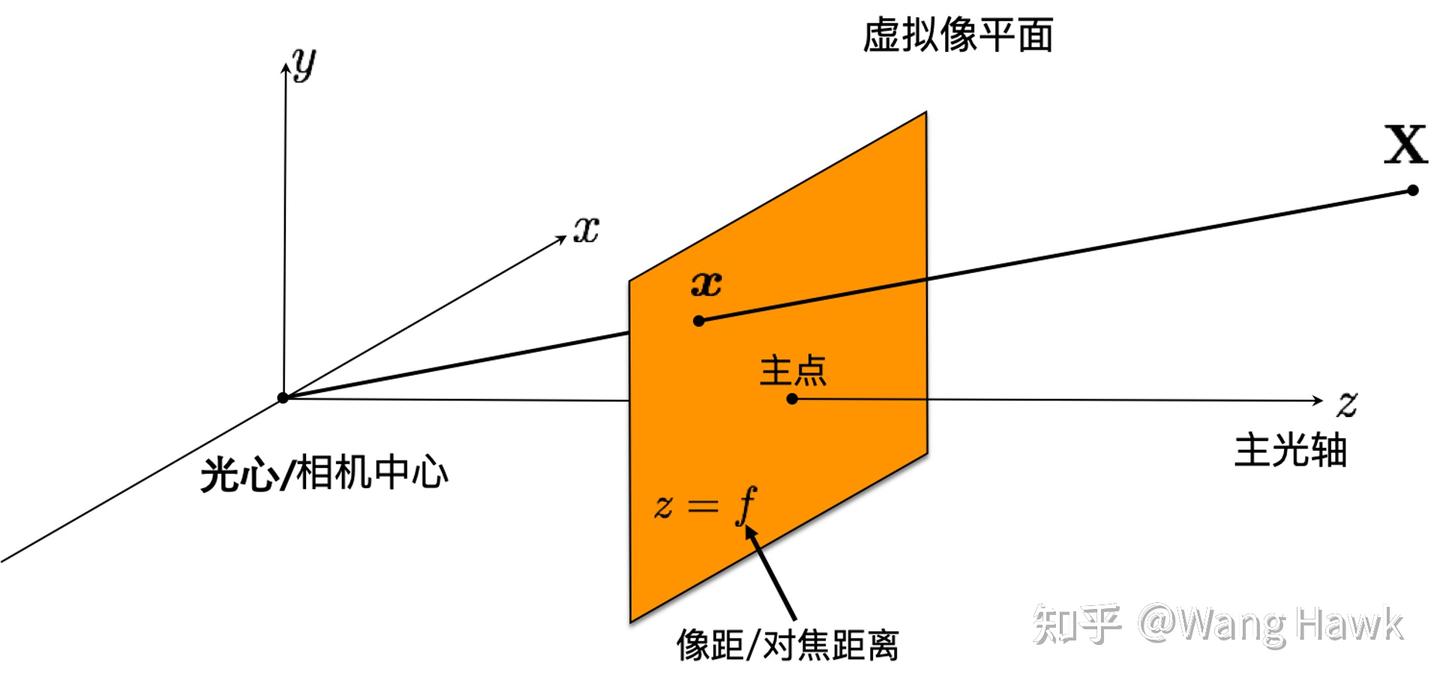
當點X投影到虛擬像平面成為點x時，從三維上講，依然是在和三維點X同一個坐標系中，原點位于光心，點x的Z值為對焦距離f。而從二維上講，我們可以認為原點位于主點，如下圖所示

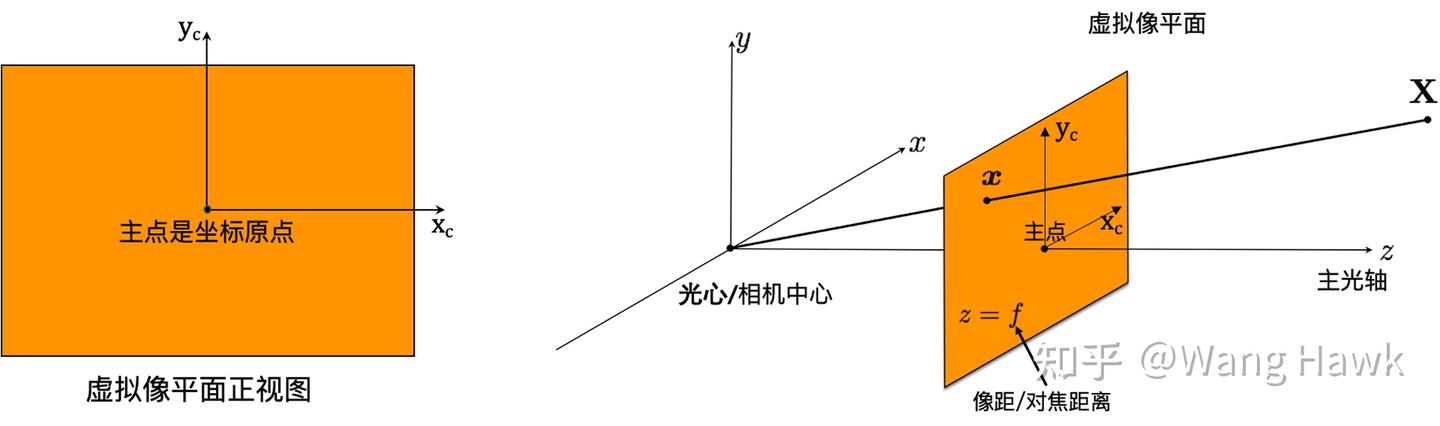
這里面就牽涉出兩個問題。

問題一：坐標原點問題

一般來說，實際圖像的坐標系原點并不是在主點。 常見的設定是將原點放置于左上角或左下角，就像下圖所示

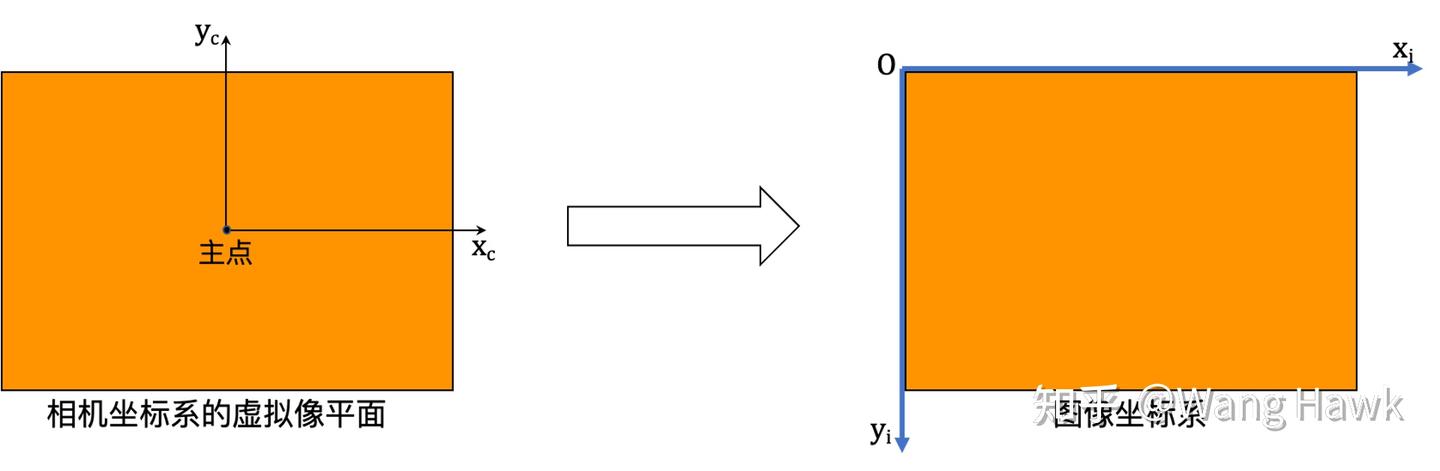
這意味著我們按照3.1節所示進行投影，得到的坐標值需要按照新老原點的相對位置進行偏移。

這樣，我們的投影矩陣需要加入偏移量：

問題二：坐標單位問題

當我們投影到虛擬像平面時，所有的單位都是不變的。 例如我們采用毫米來描述三維點相對相機光心（原點）的位置時，虛擬像平面上的像點的坐標就依然用毫米來描述。然而，真正轉換成最終的圖像時，我們習慣于用像素來描述相關的坐標。這意味著我們按照3.1節所示投影得到的坐標值，里面相關元素都需要按照毫米到像素的比例進行等比例的變化。

那么，投影矩陣進一步變為：

3.3 從世界坐標到相機坐標

我們當前在表達小孔相機的投影模型時，認為三維空間點X的坐標是位于相機坐標系的，如下圖所示：

然而，在實際的投影時，我們有時很難用相對于光心的位置來表達坐標。比如在拍攝下面這個美女時，除非經過精確的相機于她的臉部的空間關系的測量，否則我們很難表達她的右眼角相對于相機光心的物理坐標。而且就算能夠測量出來，但實際表達時也會很不自然。但如果把坐標原點定位于她的鼻尖，我們就能較為自然的表達出她臉上的任何一點的坐標了。

我們把這種方式表達的坐標叫做世界坐標，而原來相對于相機光心表達的則是相機坐標。如果你知道了一個點X的世界坐標，想知道它投影到圖像上的像素坐標，你是不能直接采用上面描述的相機投影矩陣來計算的。而是需要先把世界坐標轉換為相機坐標值。比如，上面鼻尖的世界坐標值（非齊次表達）是[0, 0, 0](單位mm)，而它相對于光心的坐標值可能是[50, 50, 500](單位mm)。

因此，為了構成一個從世界坐標系到圖像像素坐標系的完整投影矩陣，還需要考慮到上面這種坐標系的轉換。

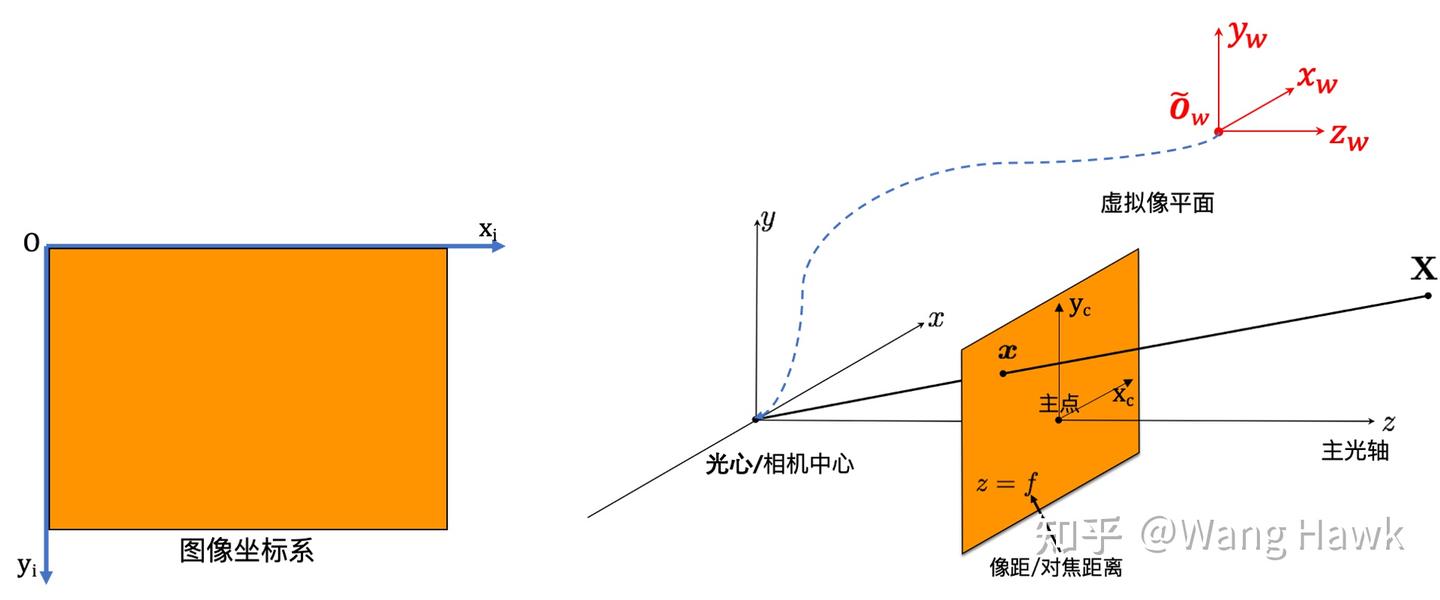
從世界坐標系到相機坐標系的變化包括兩步：

- 坐標原點平移到光心

- 各個世界坐標軸經3維旋轉到和相機坐標軸對齊

所以這是一個先平移，再旋轉的操作，用非齊次坐標表示時，是這樣的：

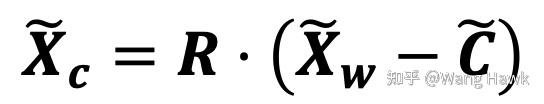
而如果用齊次坐標表達，則是：

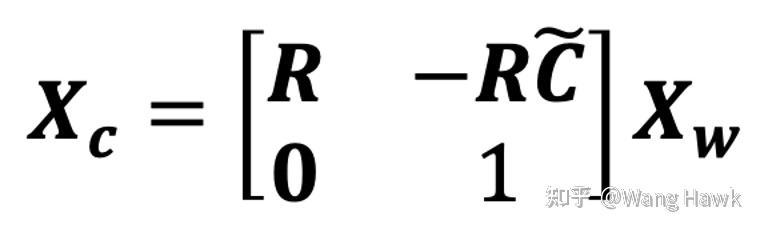
現在我們整合前面所有的變換分量，可以把從世界坐標系到圖像坐標系的變換表達如下：

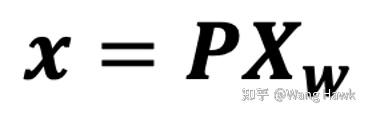
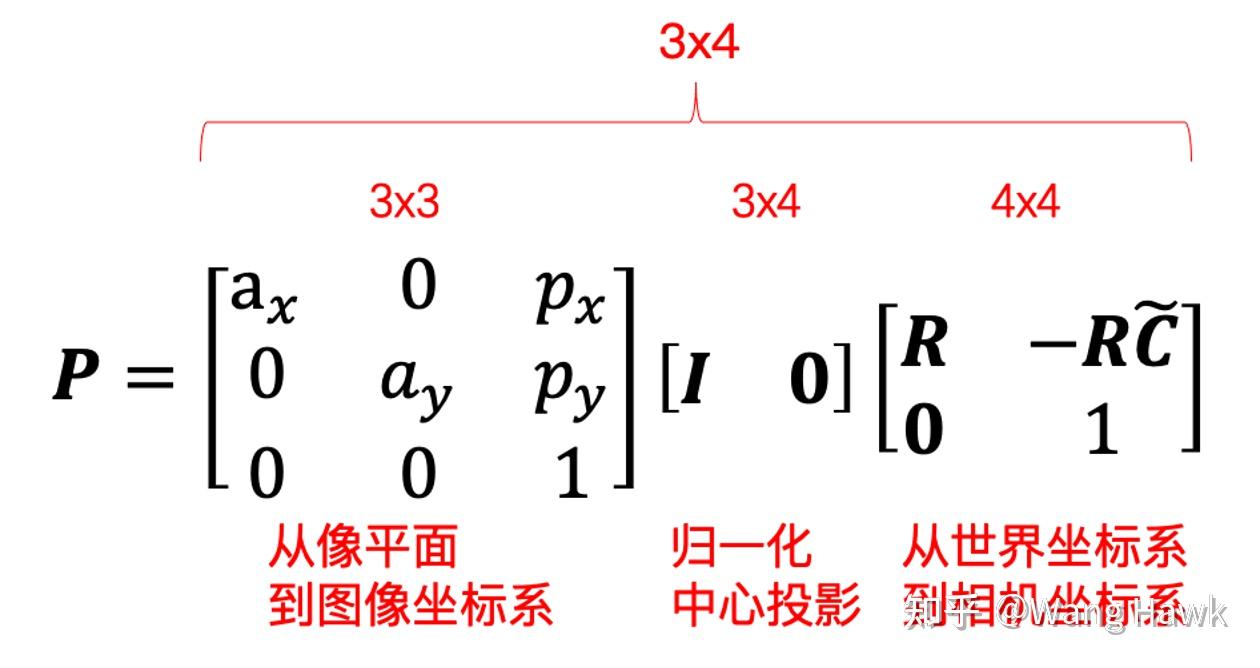
所以投影矩陣就是一個3x4的矩陣，而這個式子還可以簡潔的表示為：

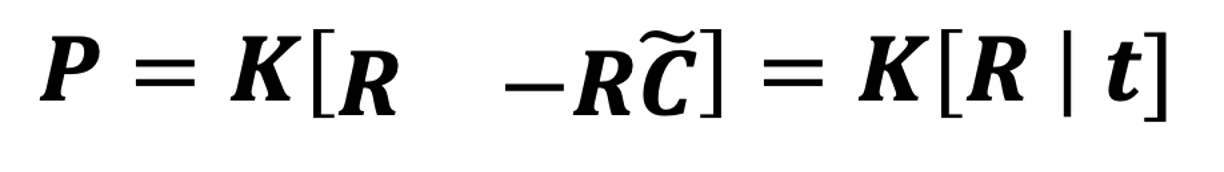
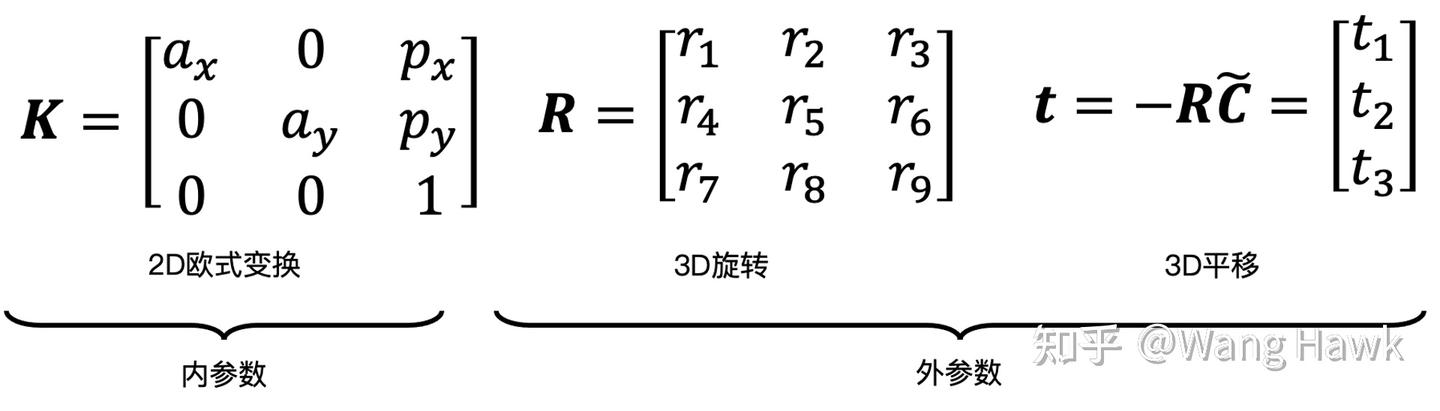
其中我們把K稱為內參，P的其余部分是外參：

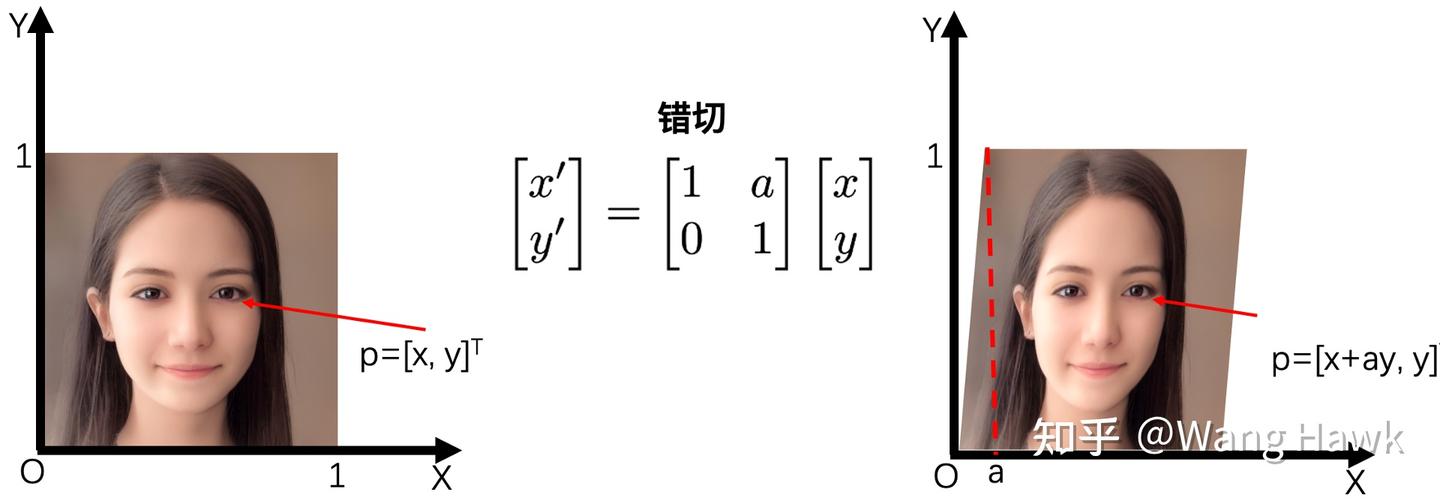
3.4 錯切的影響

現在的傳感器工藝已經非常好了，很少出現長寬不等的像素。但某些時候，我們依然要考慮這種情況，這樣K就需要另外一個元素來描述，表示如下：

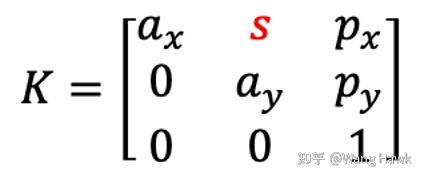
既然傳感器工藝已經不再有不方正的像素了，那么什么情況下s不為0？其中一種情況就是當我們拍攝一個已經拍攝好的照片時，比如拍一個雜志封面，如果相機和雜志間不是平行的，那么整體的投影矩陣會出現不為0的s。

總之，考慮到這個情況，整個3x4的投影矩陣的自由度就變成了11個，其中包括了5個內參數，3個旋轉分量，3個平移分量。

3.5 透視現象

前面我們已經看到，當物體投影的虛擬像平面時，坐標會等比例的變化，形成“近大遠小”的現象

我在文章手機中的計算攝影4-超廣角畸變校正中已經為你展示了透視現象的特點，現在引用其中內容如下：

人們很早就學會了利用透視效應來拍攝有趣的攝影作品：

透視投影還會使得三維空間中的平行線在畫面中相交，其交點稱作為消失點。

藝術家早就會使用透視技術，來突出主體了，例如下面這幅畫是荷蘭著名畫家約翰內斯·維米爾（Johannes Vermeer）的作品鋼琴課。畫家利用透視效應，將主人公安排在了整個畫面幾條直線的消失點上，從而實現了突出主體的作用。

然而，透視效應也會導致畫面的形變，我們看到拍攝同一個姑娘時，短焦鏡頭(廣角鏡頭)出現了強烈的透視畸變。這是因為為了拍出同樣尺寸的像，短焦鏡頭拍攝時物距更近，因為透視效應的近大遠小法則，這種形變顯得更加明顯。尤其是在近距離拍攝時，人臉上鼻子相比臉側面距離鏡頭更近，所以鼻子成像時放大得更大，于是人臉就顯得更加詭異了。

除了上面這種因為近距離拍攝導致的形變，透視效應還會導致遠離相機中心的物體被拉伸，比如下面這張用iPhone13 Mini的廣角鏡頭拍攝的照片。相比起上面因為近距離拍攝導致的形變，這種邊緣物體被拉伸的現象是我們更常見的情況。

那么問題來了，有沒有相機在成像時沒有透視效應呢？下一小節我們就來探討這個問題。

四. 其他相機模型

我們知道小孔相機因為透視效應，會呈現近大遠小的情況。下圖你可以看到Z在像坐標的分母，這也說明了這一點。

現在想想，如果我們能不斷增大Z，同時還讓f也不斷增大，并且f/Z始終是一個常量，那會怎么樣呢？

很明顯，這個時候就不再有近大遠小的現象了，不管遠近所成的像的大小都一樣！當成像系統物距很大且像距也很大時，此時的投影關系就變成了弱透視投影，成像的幾何尺寸與物距的關系就非常弱甚至沒有了。《計算機視覺中的多視角幾何》一書中的插圖形象的說明了這一點：

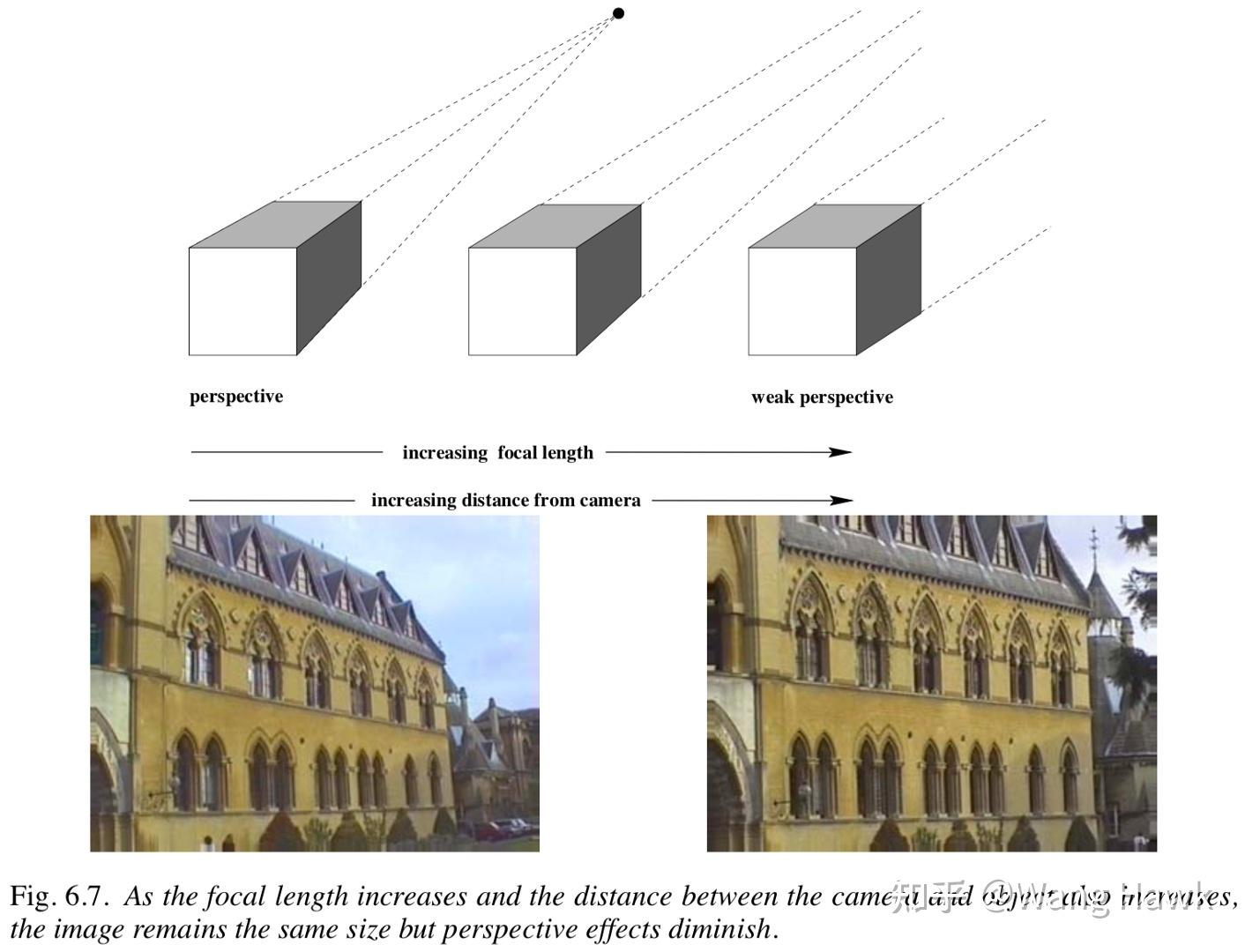
比如，當我們拍攝遠景時，此時的成像系統可以近似認為滿足弱透視投影關系

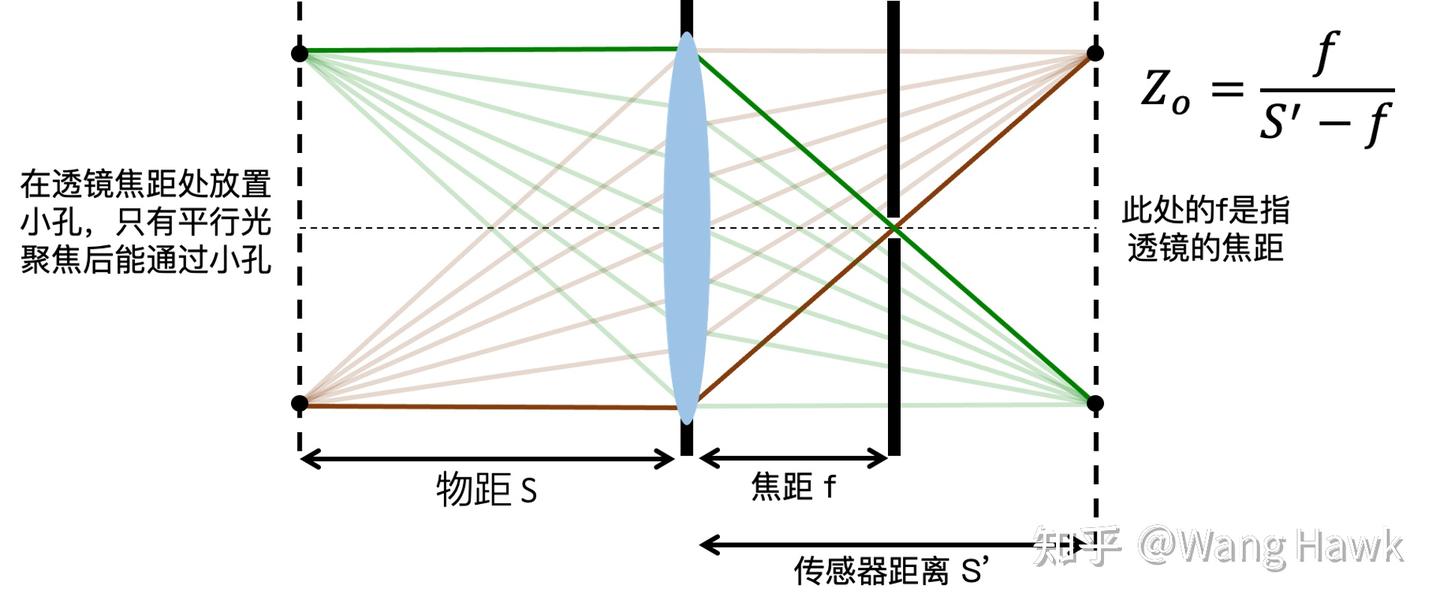
另外如果成像系統滿足如下幾何關系，也能形成弱透視投影，只要物距大于Zo，那么不管遠近成像的尺寸都與物距無關了，只與圖中中間平面的物距Zo相關。

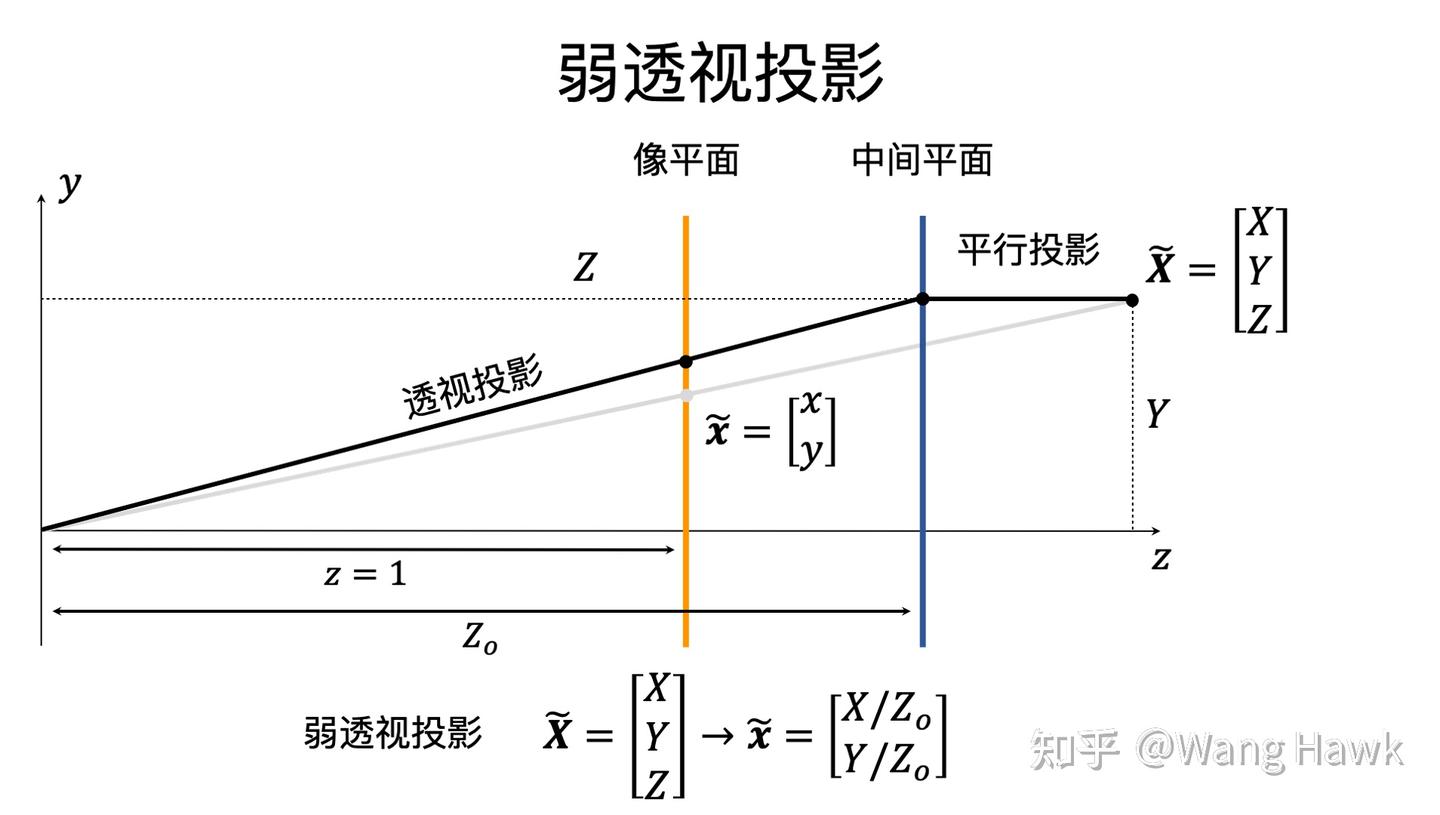
要構成這樣的投影關系也比較容易，只需要用透鏡成像+小孔成像即可。這種相機我們稱為仿射相機

那么仿射相機的投影矩陣是什么呢？

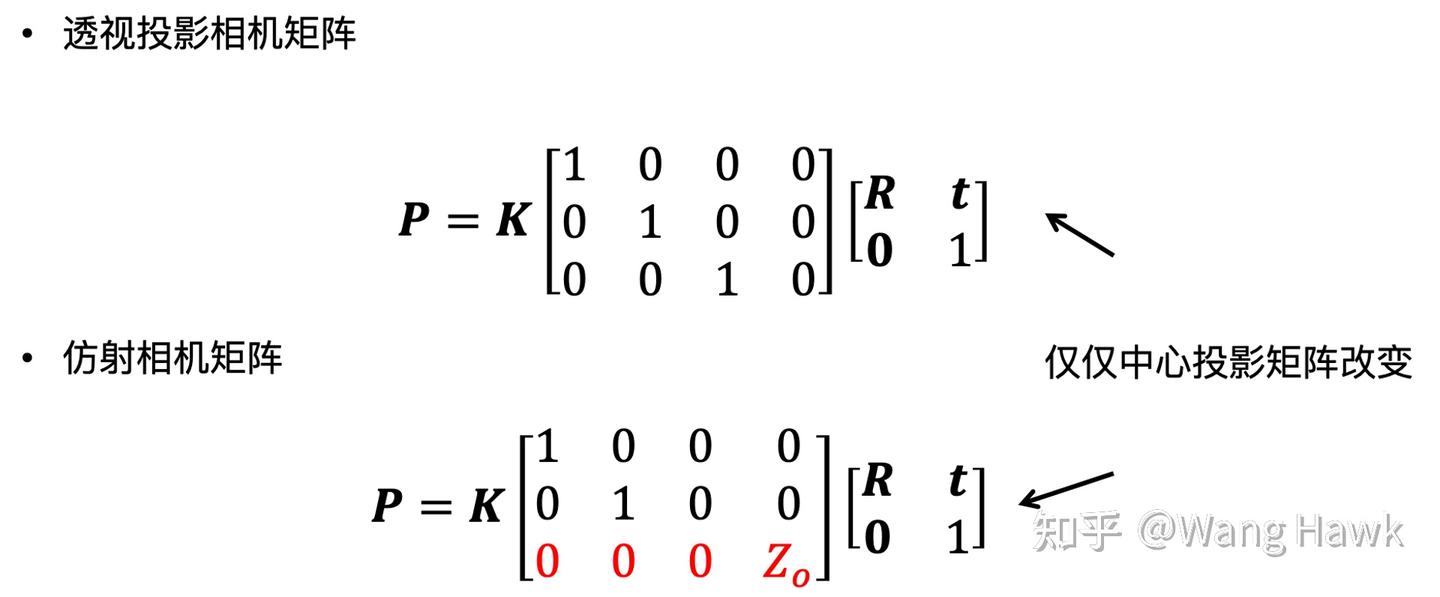
仿射相機的投影矩陣的最后一行可以轉換為[0 0 0 1]，這是它最大的特點。

如果上圖中Zo=1，會如何呢？我們看到

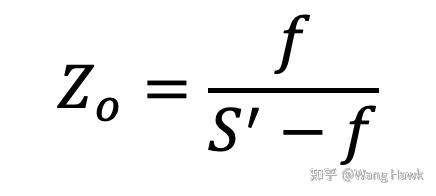
Zo=1，意味著S' = 2f，這時候小孔相機放大倍率為1, 于是投影關系就變成了所謂的正交投影

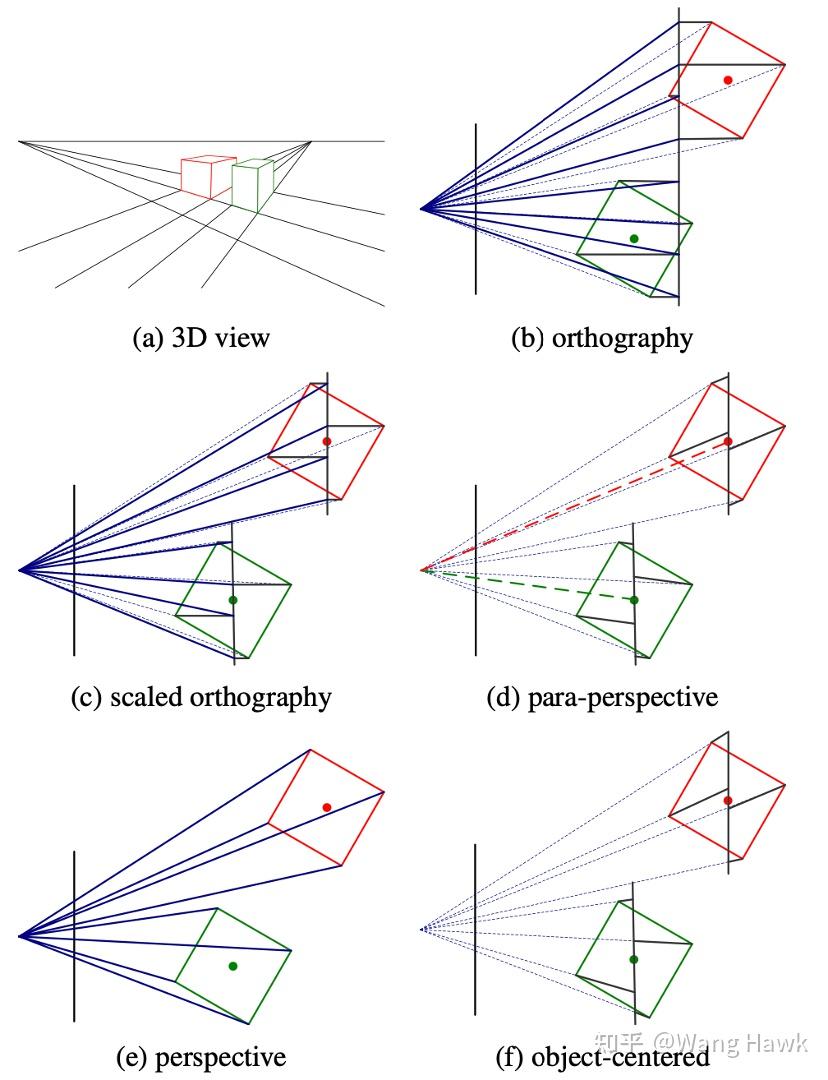
事實上，還有很多種投影方式，限于篇幅，我就不再詳述了。大家可看《計算機視覺：算法與應用》中的下圖，感受一下：

五. 總結

今天這篇文章主要回顧了小孔相機和薄透鏡成像相機的幾何模型，結合2D、3D齊次坐標和坐標變換的知識，講解了相機矩陣。我們知道了相機矩陣由幾個部分組成：內參矩陣K，以及外參矩陣，后者由投影矩陣、世界坐標系到相機坐標轉換的矩陣組合而成。對于普通的透視成像，一共有11個自由度。它包括了5個內參，3個旋轉角度，以及3個平移量。

當我們知道一個點在世界坐標系的坐標，同時又知道了投影矩陣P時，可以很容易的計算出它在圖像中的坐標。