---

前言

感覺前四道，就是考對于題目的理解能力，以及自己的模擬能力

---

A.Only One Digit

題目傳送門：Only One Digit





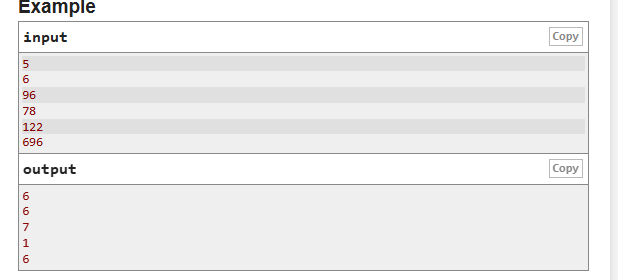
對于這一題，只要讀懂題之后，一個排序就行了
AC代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
void solve()
{string s;cin>>s;ll n[5];for(ll i=0;i<s.size();i++){n[i]=s[i]-'0';}sort(n,n+s.size());cout<<n[0]<<endl;
}
signed main()
{ll t=1;cin>>t;while(t--){solve();}return 0;
}

B.No Casino in the Mountains

題目傳送門：No Casino in the Mountains




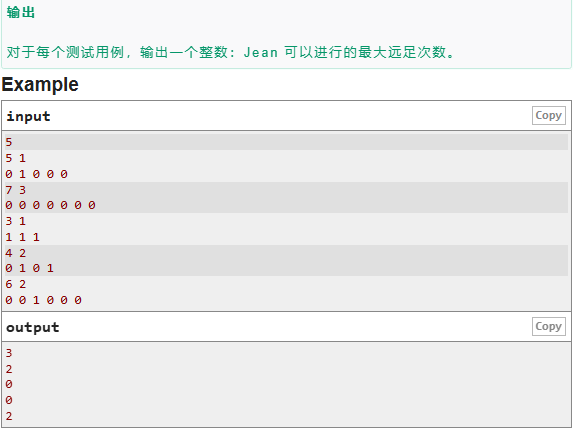
這一題由于只有0和1，故就想到了前綴和，然后再按照題目描寫的模擬一下就行了
AC代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll s[N];
ll a[N];
void solve()
{ll n,k;cin>>n>>k;ll sum=0;ll ans=0;for(ll i=1;i<=n;i++){cin>>s[i];a[i]=a[i-1]+s[i];if(s[i]==1)sum++;}if(sum==n)//特判一下是否全為1{cout<<0<<endl;return ;}ll x=0;for(ll i=1;i<=n;i++){x=i;if(s[i]==0)//為了去除開頭連續的1break;}for(ll i=x;i+k-1<=n;i++){if(a[i+k-1]-a[i]==0&&s[i]==0)//判斷一下是否滿足條件{ans++;i=i+k;}}cout<<ans<<endl;
}
signed main()
{ll t=1;cin>>t;while(t--){solve();}return 0;
}

C. I Will Definitely Make It

題目傳送門：I Will Definitely Make It


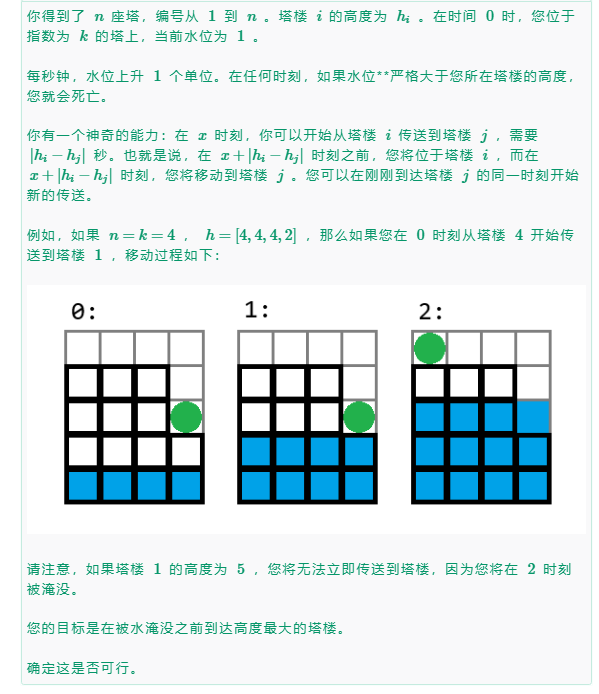
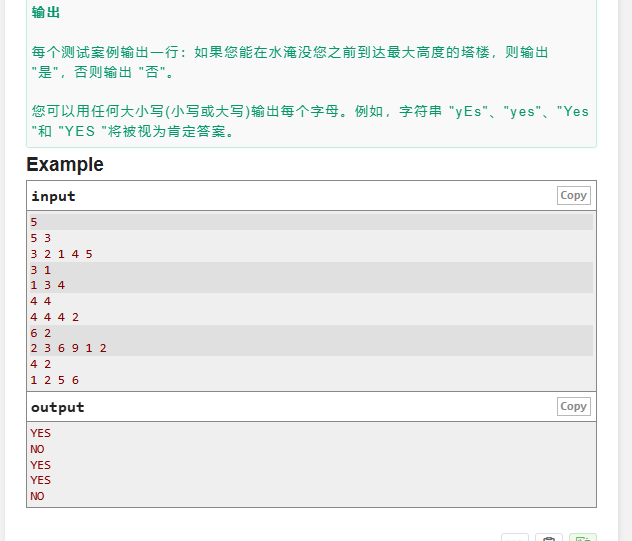
對于這一題當時快寫吐了，等到快結束的時候，又重新讀了一下題，才發現之前理解錯了，導致一直過不了，最后剩幾分鐘，也來不及改了，結束之后，重新敲了一遍，直接過了，無語。
主要思路：
通過觀察會發現當開始在哪座山時，只要之后的山與當前的位置高度小于等于，最開始山的高度，就不會被淹，只需要排完序之后，來進行判斷從最開始的山一直到最高的山是否，會出現高度差大于最開始山的高度。如果出現了就是“NO”，否則就是“YES”；
AC代碼:

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll s[N];
ll s1[N];
void solve()
{ll n,k;cin>>n>>k;for(ll i=1;i<=n;i++){cin>>s[i];}ll a=s[k],x=0;;sort(s+1,s+n+1);for(ll i=1;i<=n;i++)if(s[i]==a)x=i;ll m=1;for(ll i=x;i+1<=n;i++){s1[m++]=s[i+1]-s[i];//將高度差存入數組中}sort(s1+1,s1+m);//對其進行排序ll f=0;for(ll i=1;i<m;i++){if(s1[i]>a)//如果出現大于起始高度時就進行標記，如何跳出循環{f=1;break;}}if(f)cout<<"NO"<<endl;elsecout<<"YES"<<endl;
}
signed main()
{IOS;ll t=1;cin>>t;while(t--){solve();}return 0;
}

D.This Is the Last Time

題目傳送門：This Is the Last Time




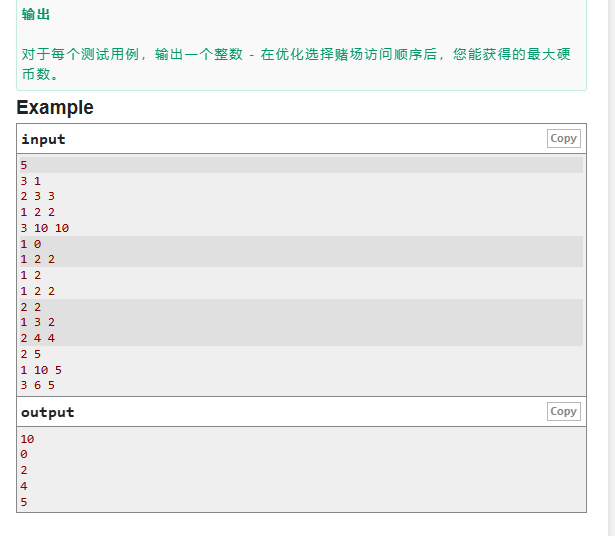
這一題就是貪心，當時只想著就進行排序，然后對其答案進行更新，沒有約束最大值，導致wa了兩發，然后改了過來，由于數組開小了，又wa了1發。WA警示自己！！！
解題思路：
這一題只需要利用結構體按照L從小到大排序，然后循環，最后再循環的時候約束一下最大值就行了。
AC代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e5+10;
struct node{ll x,y,sum;
}s[N];
bool cmd(node a,node b)
{return a.x<b.x;
}
void solve()
{ll n,k;cin>>n>>k;for(ll i=1;i<=n;i++){cin>>s[i].x>>s[i].y>>s[i].sum;}sort(s+1,s+1+n,cmd);//按照x從小到大排序ll ans=k;for(ll i=1;i<=n;i++){if(ans>=s[i].x&&ans<=s[i].y&&ans<=s[i].sum)//如果大于sum，則進行更新，ans=s[i].sum;}cout<<ans<<endl;
}
signed main()
{ll t=1;cin>>t;while(t--){solve();}return 0;
}

E.G-C-D, Unlucky!

題目傳送門：E.G-C-D, Unlucky!




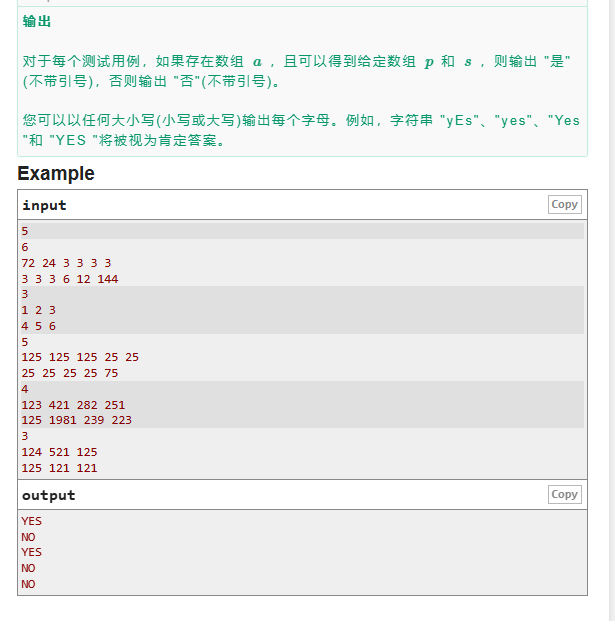
解題思路：
這一題就是找規律題，
1. 通過前綴與后綴的定義就會發現，前綴與后綴數組，到最后都是包含了所有數；故前綴數組的最后一個數與后綴數組的第一個數應該相同。
2. 由于公約數是求兩個數的公因數，而公因數都是小于等于這這兩個數最小的本身，由此可以得到，其數組必定是單調的

前綴: 非單調遞增。

后綴：非單調遞減。

3. 就是公約數的性質了


AC代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll a[N],b[N],c[N];
ll lcm(ll x,ll y)
{return x*y/__gcd(x,y);
}
void solve()
{ll n;cin>>n;for(ll i=1;i<=n;i++)cin>>a[i];for(ll i=1;i<=n;i++)cin>>b[i];if(a[n]!=b[1]){cout<<"NO"<<endl;return ;}for(ll i=1;i+1<=n;i++){if(a[i]<a[i+1]){cout<<"NO"<<endl;return ;}}for(ll i=1;i+1<=n;i++){if(b[i]>b[i+1]){cout<<"NO"<<endl;return ;}}for(ll i=1;i<=n;i++){ll l=lcm(a[i],b[i]);if(i>1&&__gcd(a[i-1],l)!=a[i]){cout<<"NO"<<endl;return;}if(i+1<=n&&__gcd(b[i+1],l)!=b[i]){cout<<"NO"<<endl;return;}}cout<<"YES"<<endl;
}
signed main()
{IOS;ll t=1;cin>>t;while(t--){solve();}return 0;
}

lcm(a[i],b[i])
a[i]=p[i];
b[i]=s[i];
如果從傳遞性來進行推理的話

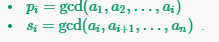
lcm求出來的就是a[i]然后再利用傳遞性與p[i-1]求最大公因數

構造的核心思想：
對于每個位置 i，構造候選的數組 a 元素為 a[i]（前綴 GCD）和 b[i]（后綴 GCD）的最小公倍數 l。因為 a 數組的元素需要同時是前綴 GCD 和后綴 GCD 的倍數，最小公倍數是滿足該條件的最小可能值 。

---

總結

不知道是在協會敲代碼，敲習慣了，看著大屏幕，很少分神。然而到了寢室看自己的電腦敲代碼，總是很難集中注意看題。總是看著題目讀著讀著心神就飄到其他地方去了~~~~
嗯，集中注意力，下回必須集中注意力！！！