Adversarial Schr?dinger Bridge Matching

公眾號：EDPJ（進 Q 交流群：922230617 或加 VX：CV_EDPJ 進 V 交流群）?

目錄

0. 摘要

1. 簡介

4. 實驗

---

0. 摘要

薛定諤橋（Schr?dinger Bridge，SB）問題提供了一個結合最優輸運（optimal transport）和擴散模型的強大框架。一個解決 SB 問題的有前景的新方法是迭代馬爾可夫擬合（Iterative Markovian Fitting，IMF），它在連續時間隨機過程的馬爾可夫和倒向投影（reciprocal projection）之間交替。然而，由于使用了許多步的隨機微分方程數值求解器，IMF 程序構建的模型推理時間較長。為了解決這個限制，我們提出了一種新的離散時間 IMF（D-IMF），其中隨機過程的學習被替換為僅在離散時間內學習幾個轉移概率。其主要優點是它在實踐中可以自然地通過去噪擴散 GAN（DD-GAN）實現，這是一種已經很成熟的對抗生成建模技術。我們展示了我們的 D-IMF 程序可以在僅用幾步生成代替數百步生成的情況下，提供與 IMF 相同質量的無監督域遷移。

（2022|ICLR，擴散 GAN，少量步擴散，對抗散度，非飽和 GAN）用去噪擴散 GAN 解決生成學習難題_高樣本質量、模式覆蓋和快速采樣-CSDN博客?

1. 簡介

貢獻。本論文通過引入一種新方法來學習薛定諤橋（Schr?dinger Bridge），解決了現有迭代馬爾可夫擬合（IMF）框架推理時間較長的限制。

• 理論 I。我們引入了離散迭代馬爾可夫擬合（D-IMF）（sec. 3.2, 3.3），創新性地應用離散馬爾可夫投影來解決薛定諤橋問題，而不依賴隨機微分方程。這一方法顯著簡化了推理過程，使其在理論上僅需幾步評估即可完成。

• 理論 II。我們推導了處理高維高斯分布時 D-IMF 程序的閉式（closed-form）更新公式。這一進展允許對我們方法的收斂率進行詳細的實證分析，并增強其理論基礎（sec. 3.4, 4.1）。

• 實踐。對于通過樣本獲得的一般數據分布，我們提出了一種算法（Adversarial Schr?dinger Bridge Matching，ASBM）來實際實現離散馬爾可夫投影和我們的 D-IMF（sec. 4.2）。我們的算法基于對抗學習和去噪擴散 GAN [49]。我們學習的 SB 模型在推理中僅使用 4 步評估（sec. 3.5），而不是基礎 IMF [43] 的數百步。

4. 實驗

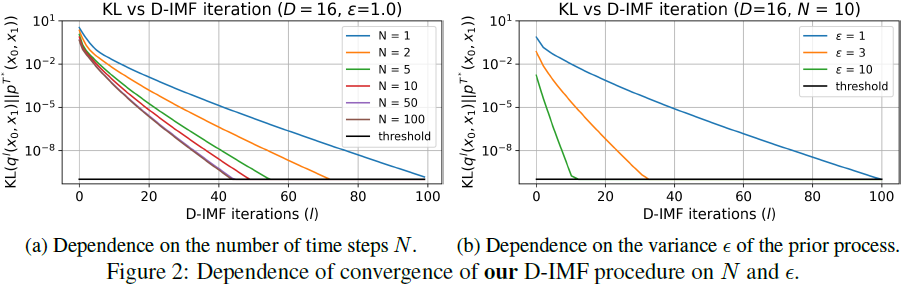
我們通過使用 sec. 3.4 中的 D-IMF 解析公式進行實驗。我們遵循 [12] 中的設置，并考慮維度 D = 16 和 ?∈{1,3,10} 的中心高斯分布 p0=N(0,Σ0) 和 p1=N(0,Σ1) 的薛定諤橋問題。?

我們發現，在所有情況下，我們的 D-IMF 過程顯示出指數級的收斂速度。如圖 2a 所示，收斂速度對時間步 N 的依賴性迅速飽和。因此，即使只有幾個時間點，例如 N = 5，也能提供快速的收斂速度。從圖 2b 可以明顯看出，收斂速度受參數 ? 的選擇影響很大。例如，從 ?=1 到 ?=10 的過渡需要多十倍的 D-IMF 迭代次數。因此，這個超參數在實際問題中可能非常重要。?

Diffusion schr?dinger bridge matching（DSBM）?