數據結構·一篇搞定隊列！

hello，大家好啊，肖恩又拖更了，你們聽我狡辯，前段時間有期中考試，so我就沒什么時間寫這個，在這給大家道個歉😭😭😭
請添加圖片描述
我后面一定盡力不拖更
那么接下來，我們來看隊列這個數據結構

引言

隊列是另一種常見的數據結構,它遵循"先進先出"(FIFO)的原則。隊列通常用于存儲等待處理的任務或數據,如任務調度、資源分配等。了解隊列的基本概念和實現方式對于掌握算法和數據結構同樣很重要。

隊列的概念及結構

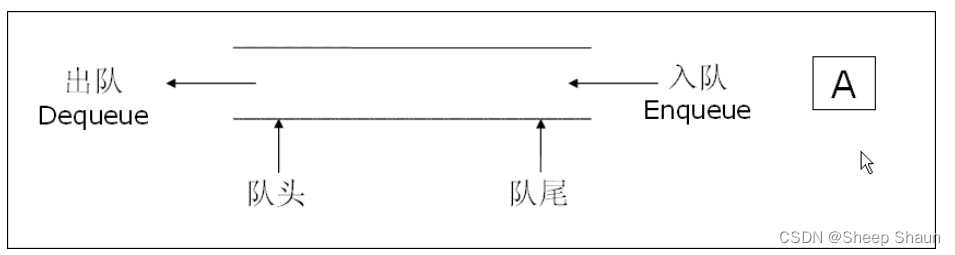
隊列：只允許在一端進行插入數據操作，在另一端進行刪除數據操作的特殊線性表，隊列具有先進先出
FIFO(First In First Out) 入隊列：進行插入操作的一端稱為隊尾出隊列：進行刪除操作的一端稱為隊頭
在這里插入圖片描述

隊列的實現

隊列也可以數組和鏈表的結構實現，使用鏈表的結構實現更優一些，因為如果使用數組的結構，出隊列在數
組頭上出數據，效率會比較低。
那我們下面來實現隊列的一些操作
因為也不是很難，我直接附上代碼

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>typedef int QDataType;typedef struct QueueNode
{struct QueueNode* next;QDataType val;
}QNode;typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;
//初始化
void QueueInit(Queue* pq) {assert(pq);pq->phead = pq->ptail = NULL;pq->size = 0;
}
//銷毀
void QueueDestroy(Queue* pq) {assert(pq);QNode* cur = pq->phead;while (cur) {QNode* next = cur->next;free(cur);cur = next;}pq->phead = pq->ptail == NULL;pq->size = 0;
}// 隊尾插入
void QueuePush(Queue* pq, QDataType x) {assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");return;
}newnode->next = NULL;newnode->val = x;if (pq->phead == NULL)pq->phead = pq->ptail = newnode;elsepq->ptail->next = newnode;pq->ptail = newnode;pq->size++;
}
// 隊頭刪除
void QueuePop(Queue* pq) {assert(pq);assert(pq->size != 0);if (pq->phead->next = NULL) {free(pq->phead);pq->phead = pq->ptail = NULL;}else {QNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}pq->size--;
}// 取隊頭和隊尾的數據
QDataType QueueFront(Queue* pq) {assert(pq && pq->phead);return pq->phead->val;
}QDataType QueueBack(Queue* pq) {assert(pq && pq->ptail);return pq->ptail->val;
}
// 獲取隊列中有效元素個數
int QueueSize(Queue* pq) {assert(pq);return pq->size;
}
// 檢測隊列是否為空
bool QueueEmpty(Queue* pq) {assert(pq);return pq->size == 0;
}

簡單說兩個主要的操作

隊尾插入 (QueuePush):
- 首先檢查傳入的隊列指針是否為空,如果為空則拋出錯誤。
- 分配一個新的節點內存空間。
- 將新節點的 next 指針設置為 NULL,并將待插入的數據 x 存儲到節點的 val 字段。
- 如果隊列為空,則將新節點同時設置為頭指針 phead 和尾指針 ptail。
- 否則,將當前尾節點的 next 指針指向新節點,并更新尾指針 ptail 指向新節點。
- 最后將隊列大小 size 加 1。
隊頭刪除 (QueuePop):
- 首先檢查傳入的隊列指針是否為空,如果為空則拋出錯誤。
- 檢查隊列是否為空,如果為空則什么也不做直接返回。
- 如果隊列只有一個節點,則釋放該節點并將頭尾指針都設置為 NULL。
- 否則,獲取頭節點的下一個節點,釋放頭節點,并將頭指針 phead 指向下一個節點。
- 最后將隊列大小 size 減 1。

通過這兩個基本操作,我們可以實現一個基于鏈表的隊列數據結構,支持向隊列尾部添加元素和從隊列頭部刪除元素的功能。

實際中我們有時還會使用一種隊列叫循環隊列。環形隊列可以使用數組實現，也可以使用循環鏈表實現。
使用循環隊列的優點是可以高效地利用數組空間,避免了普通隊列在刪除元素時,需要移動所有剩余元素的問題。但同時也需要額外維護頭尾指針,增加了一定的復雜度。

循環隊列在某些場景下,如緩存管理、生產者-消費者模型等,能夠發揮出較好的性能表現。
那么下面的一個面試題（也是考研題）就讓我們來看看循環隊列。

例題

設計循環隊列
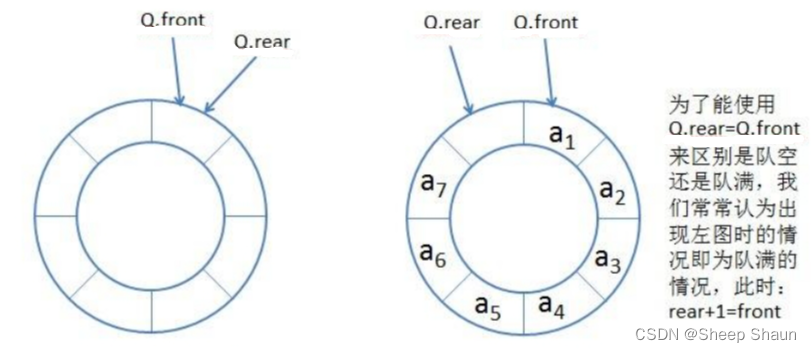
在這里插入圖片描述

使用動態數組很方便
我相信下面詳細的注釋能讓你明白循環隊列是怎么回事，不是很理解的話，可以自己畫圖來便于理解

// 定義循環隊列結構體
typedef struct {int *a;  // 存儲隊列元素的動態數組int head; // 隊頭下標int tail; // 隊尾下標int k;    // 隊列最大容量
} MyCircularQueue;// 檢查隊列是否為空
bool myCircularQueueIsEmpty(MyCircularQueue *obj) {return obj->head == obj->tail; // 當 head 和 tail 相等時,隊列為空
}// 檢查隊列是否已滿
bool myCircularQueueIsFull(MyCircularQueue *obj) {return (obj->tail + 1) % (obj->k + 1) == obj->head; // 當 (tail + 1) % (k + 1) 等于 head 時,隊列已滿
}// 創建一個容量為 k 的循環隊列
MyCircularQueue *myCircularQueueCreate(int k) {MyCircularQueue *p = (MyCircularQueue *)malloc(sizeof(MyCircularQueue)); // 分配 MyCircularQueue 結構體的內存p->a = (int *)malloc((k + 1) * sizeof(int));    // 分配存儲元素的動態數組p->k = k;                   // 設置隊列最大容量p->head = p->tail = 0;  // 初始化 head 和 tail 為 0return p;
}// 向隊列中添加一個元素
bool myCircularQueueEnQueue(MyCircularQueue *obj, int value) {if (myCircularQueueIsFull(obj))  // 如果隊列已滿,返回 falsereturn false;obj->a[obj->tail] = value;  // 將元素添加到隊尾obj->tail = (obj->tail + 1) % (obj->k + 1); // 更新 tail 下標,實現循環return true;}// 從隊列中刪除一個元素
bool myCircularQueueDeQueue(MyCircularQueue *obj) {if (myCircularQueueIsEmpty(obj)) { // 如果隊列為空,返回 falsereturn false;} else {obj->head = (obj->head + 1) % (obj->k + 1); // 更新 head 下標,實現刪除隊頭元素return true;}
}// 獲取隊頭元素
int myCircularQueueFront(MyCircularQueue *obj) {if (obj->tail == obj->head) { // 如果隊列為空,返回 -1return -1;} else {return obj->a[obj->head]; // 返回隊頭元素}
}// 獲取隊尾元素
int myCircularQueueRear(MyCircularQueue *obj) {if (obj->tail == obj->head) { // 如果隊列為空,返回 -1return -1;} else {return obj->a[(obj->tail + obj->k) % (obj->k + 1)]; // 返回隊尾元素}
}// 釋放循環隊列占用的內存空間
void myCircularQueueFree(MyCircularQueue *obj) {free(obj->a); // 釋放存儲元素的動態數組free(obj);     // 釋放 MyCircularQueue 結構體
}

循環隊列的存儲空間為 Q(1:100) ，初始狀態為 front=rear=100 。經過一系列正常的入隊與退隊操作
后， front=rear=99 ，則循環隊列中的元素個數為（）
A. 1
B. 2
C. 99
D. 0或者100

現有一循環隊列，其隊頭指針為front，隊尾指針為rear；循環隊列長度為N。其隊內有效長度為？(假設
隊頭不存放數據)
A. (rear - front + N) % N + 1
B. (rear - front + N) % N
C. (rear - front) % (N + 1)
D. (rear - front + N) % (N - 1)

解析：
在循環隊列中，隊頭指針 front 指向隊首元素的下一個位置（如果隊頭不存放數據），而隊尾指針 rear 指向隊尾元素的下一個位置。這意味著當隊列為空時，front 和 rear 通常指向同一個位置（或者在某些實現中，rear 可能在 front 的下一個位置，具體取決于如何定義“空”狀態）。

隊列的有效長度（即隊列中元素的數量）可以通過計算 rear 和 front 之間的差值來得到，但是需要注意這是一個循環結構，所以差值需要用模運算 % N 來處理。

假設 front 和 rear 的初始值都是 0（隊列為空），并且每次入隊操作 rear 會遞增，每次出隊操作 front 會遞增，那么隊列的有效長度可以用以下公式計算：

(rear - front + N) % N
這里加 N 是為了確保在 rear 小于 front 的情況下（即隊列繞了一圈之后），差值仍然是正數。然后取模 N 來得到一個 0 到 N-1 之間的值，這個值就是隊列的有效長度。

注意：這個公式假設 front 和 rear 的初始值都是 0，并且每次操作后都會遞增。如果初始值不是 0，或者有其他特殊的入隊/出隊邏輯，那么可能需要調整這個公式。
那么到這里，基本上隊列的東西都講完啦
在這里插入圖片描述
下一篇講隊列和棧的相互實現~~~
待會兒見
請添加圖片描述