@toc

🤚我的博客

• 歡迎光臨我的博客：https://blog.csdn.net/qq_52434217?type=blog

🥛前言

動態規劃是常見的算法思路，動態規劃在計算過程中保存了部分計算結果到內存中，以便于在進行下一次計算時可以直接從內存中獲取到而不用再進行計算，可以降低時間復雜度。

動態規劃也一直都是一個比較難以形成思路的算法思想。這篇文章雖然是一個簡單題，但是記錄了動態規劃算法的解題思路，方便形成一個固定的解題思路。

📖題目

給你一個整數 n ，請你生成并返回所有由 n 個節點組成且節點值從 1 到 n 互不相同的不同 二叉搜索樹 。可以按 任意順序 返回答案。

示例：

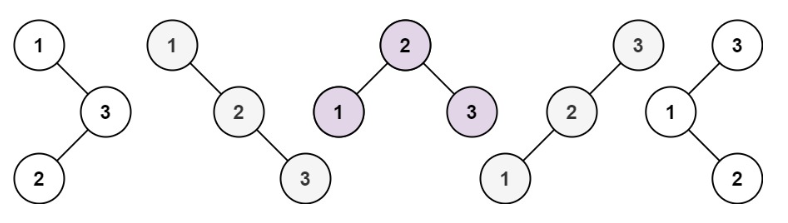
輸入： n = 3

輸出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

📖二叉搜索樹

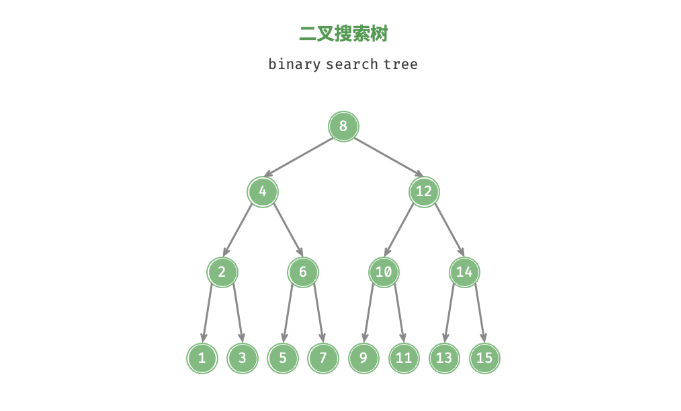
二叉搜索樹滿足兩個條件：

1、對于根節點而言，左子節點的值<根節點<右子節點的值。

2、對于任意節點而言，都滿足條件1。

📖解題

🤔思考過程

既然題目以二叉樹為背景，那么考察的算法大概率是回溯。所謂回溯，是指是一種通過窮舉來解決問題的方法，它的核心思想是從一個初始狀態出發，暴力搜索所有可能的解決方案，當遇到正確的解則將其記錄，直到找到解或者嘗試了所有可能的選擇都無法找到解為止。回溯算法通常采用“深度優先搜索”來遍歷解空間。

對于此題而言，我們需要列舉每一個根節點的情況，假設輸入n=3時，需要考慮根節點分別為1,2,3的情況。即在[1,n]中枚舉。并且在枚舉的過程中，結合二叉搜索樹的性質，對回溯的遞歸函數做一些邊界條件的限制。

前面介紹了，二叉搜索樹的性質是ndoe.lef.val < node.val < node.right.val。那么就可以在[1,i-1]中枚舉左節點，在[i+1,n]枚舉右節點。而這樣的問題又可以進一步轉化成在[1,i-1]中構造二叉搜索樹的子問題。便可以采用遞歸的方法解決此問題，在每一次遞歸中都采用回溯法枚舉不同的情況。

🤏思路轉化代碼

分析過程清楚了，但是如何將分析思路轉化成代碼呢。

首先要清楚遞歸函數怎么寫。在分析過程中我們表述了如何去枚舉一個二叉搜索樹，那么這個遞歸函數就是用于枚舉不同情況的搜索樹。定義遞歸函數為dfs(start,end)，這個函數用于返回不同根節點的二叉樹。同時這個函數能夠將問題轉化成子問題，也就是左子樹和右子樹。那么就可以進一步轉化成dfs(letf,i-1)和dfs(i+1,right)。然后我們需要將樹的結構用數組保存下來，在左子樹和右子樹中選擇一棵樹拼接到根節點即可。

轉化成代碼如下

def dfs(start,end):ans = []for i in range(start,end):# 枚舉左子樹left = dfs(start,i-1)# 枚舉右子樹right = dfs(i+1,right)for x in left:for y in right:root = TreeNode(i)root.left,root.right = x,yans.append(root)return ans

我們完成了函數的核心功能，但是需要考慮到一個邊界情況：當start>end時，應該怎么處理？

這里只需要處理成返回[None]即可。因為這種情況不可能存在。

所以這個函數的完整代碼如下

def dfs(start,end):if start > end:return [None]ans = []for i in range(start,end):# 枚舉左子樹left = dfs(start,i-1)# 枚舉右子樹right = dfs(i+1,right)for x in left:for y in right:root = TreeNode(i)root.left,root.right = x,yans.append(root)return ans

到這里我們就可以寫出整個題目的代碼了，為了便于debug，這里把打印函數也寫出來了。

# from typing import List,Optionalclass TreeNode:def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = rightself.res = []def preorder(root,res):if root:res.append(root.val)preorder(root.left,res)preorder(root.right,res)else:res.append(None)return resclass Solution:def generateTrees(self, n: int) -> List[Optional[TreeNode]]:def dfs(l,r):if l > r:return [None]ans = []for i in range(l,r+1):for x in dfs(l,i-1):for y in dfs(i+1,r):root = TreeNode(i)root.left,root.right=x,yans.append(root)return ansreturn dfs(1,n)if __name__ =='__main__':s = Solution()r = s.generateTrees(3)for i in r:print(preorder(i,[]))

💠END

數據結構與算法題還在繼續更新，雖然是學習的大佬的思路。但是自己能進行輸出也是一種學習的方法和技巧。

一起加油！🆙🆙🆙

🏕?公眾號

歡迎關注小夜的公眾號，一個立志什么都能會的研究生。有不懂的地方請留言踢我！

---