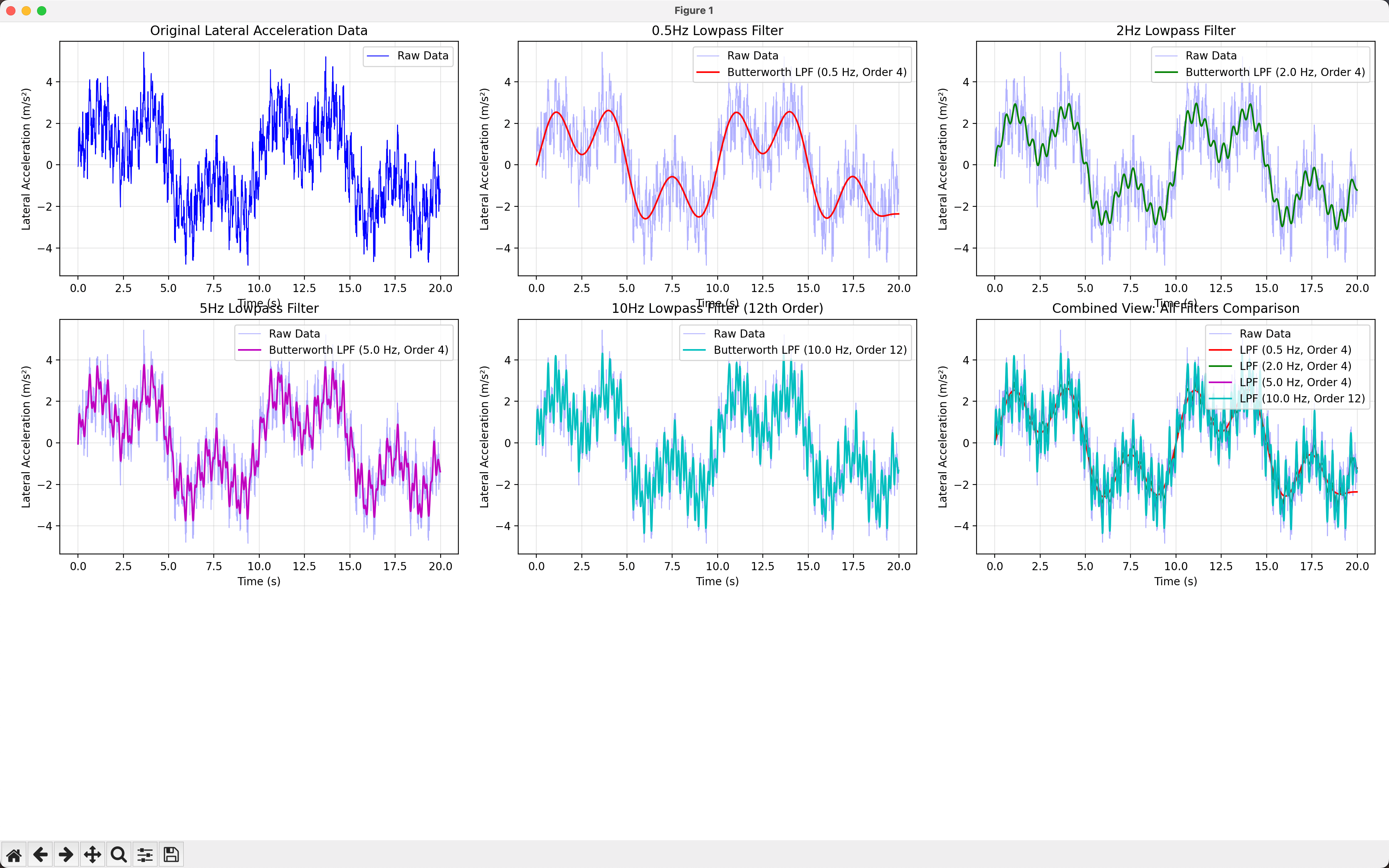
在自動駕駛的宏大敘事中,我們常常聚焦于人工智能、深度學習、高精地圖等"明星技術"。然而,在這些耀眼的光環背后,有一個低調卻至關重要的"幕后英雄"——濾波器。它不僅是信號處理的工具,更是連接物理世界與數字算法的橋梁,是自動駕駛感知、決策、控制乃至測試驗證的數學基石。
本文將帶你深入濾波器的世界,從車輛加速度的噪聲抑制,到其在自動駕駛系統中的核心應用,再到測試驗證中的關鍵抉擇,揭示其如何從一個簡單的數學公式,演變為決定系統成敗的"雙刃劍"。我們將補充常用濾波器的核心公式,并提供不同應用場景下的選擇指南。
第一重境界:降噪——讓信號回歸真實
想象一輛車在顛簸的路面上行駛。其搭載的加速度計會忠實地記錄下每一個微小的振動——輪胎碾過石子、懸掛系統彈跳、發動機抖動。這些高頻噪聲,與車輛真正加速、減速或轉彎產生的低頻慣性力混雜在一起,形成了我們常說的"臟信號"。
如果直接使用這種信號計算速度或位移,高頻噪聲會在積分過程中被急劇放大,導致結果嚴重失真。例如,一次平穩的剎車過程,可能在計算出的"速度曲線"上表現為劇烈的震蕩。這便是濾波器登場的時刻。
目標:保留反映車輛真實運動的低頻信息,抑制無用的高頻噪聲。
常用方法與核心公式:
| 濾波器類型 | 核心公式 | 說明 |
|---|---|---|
| 移動平均 (Moving Average) | y[n]=1N∑k=0N?1x[n?k] y[n] = \frac{1}{N} \sum_{k=0}^{N-1} x[n-k] y[n]=N1?k=0∑N?1?x[n?k] | 計算最近N個采樣點的算術平均。實現簡單,但延遲大(約 N?12\frac{N-1}{2}2N?1? 個周期),會削弱信號峰值。 |
| 一階低通 (First-Order Low-Pass) | y[n]=α?x[n]+(1?α)?y[n?1] y[n] = \alpha \cdot x[n] + (1 - \alpha) \cdot y[n-1] y[n]=α?x[n]+(1?α)?y[n?1] 其中 α=dtτ+dt,τ=12πfc \alpha = \frac{dt}{\tau + dt},\quad \tau = \frac{1}{2\pi f_c} α=τ+dtdt?,τ=2πfc?1? | dt為采樣周期,fc為截止頻率。通過調整fc控制平滑程度。相位延遲小于移動平均,廣泛用于車載ECU。 |
| 卡爾曼濾波 (Kalman Filter) | 預測: x^?[k]=Fx^[k?1]+Bu[k] \hat{\mathbf{x}}^{-}[k] = \mathbf{F}\hat{\mathbf{x}}[k-1] + \mathbf{B}\mathbf{u}[k] x^?[k]=Fx^[k?1]+Bu[k] P?[k]=FP[k?1]FT+Q \mathbf{P}^{-}[k] = \mathbf{F}\mathbf{P}[k-1]\mathbf{F}^T + \mathbf{Q} P?[k]=FP[k?1]FT+Q 更新: K[k]=P?[k]HT(HP?[k]HT+R)?1 \mathbf{K}[k] = \mathbf{P}^{-}[k]\mathbf{H}^T(\mathbf{H}\mathbf{P}^{-}[k]\mathbf{H}^T + \mathbf{R})^{-1} K[k]=P?[k]HT(HP?[k]HT+R)?1 x^[k]=x^?[k]+K[k](z[k]?Hx^?[k]) \hat{\mathbf{x}}[k] = \hat{\mathbf{x}}^{-}[k] + \mathbf{K}[k](\mathbf{z}[k] - \mathbf{H}\hat{\mathbf{x}}^{-}[k]) x^[k]=x^?[k]+K[k](z[k]?Hx^?[k]) P[k]=(I?K[k]H)P?[k] \mathbf{P}[k] = (\mathbf{I} - \mathbf{K}[k]\mathbf{H})\mathbf{P}^{-}[k] P[k]=(I?K[k]H)P?[k] | 線性系統的最優估計算法。F\mathbf{F}F為狀態轉移矩陣,H\mathbf{H}H為觀測矩陣,Q\mathbf{Q}Q和R\mathbf{R}R分別為過程噪聲和觀測噪聲協方差。需要建立準確的系統模型。 |
| 擴展卡爾曼濾波 (EKF) | 同KF,但F\mathbf{F}F和H\mathbf{H}H替換為非線性函數f()f()f()和h()h()h()的雅可比矩陣。 | 用于非線性系統(如車輛運動學)。通過局部線性化近似處理非線性。 |
| 互補濾波 (Complementary Filter) | θest=α?(θprev+ω?dt)+(1?α)?θacc \theta_{est} = \alpha \cdot (\theta_{prev} + \omega \cdot dt) + (1 - \alpha) \cdot \theta_{acc} θest?=α?(θprev?+ω?dt)+(1?α)?θacc? | 融合陀螺儀(高頻準)和加速度計(低頻準)。ω\omegaω為角速度,θacc\theta_{acc}θacc?為由加速度計計算的姿態角。α\alphaα通常接近1。 |
本質:這一境界的濾波器,是信號的"清潔工",旨在還原物理世界的真實動態。
第二重境界:融合——在不確定性中構建認知
當自動駕駛車輛駛上道路,它不再僅僅依賴單一傳感器。激光雷達、攝像頭、毫米波雷達、GPS、IMU、輪速計……多種傳感器從不同維度感知環境。然而,每個傳感器都有其局限:攝像頭怕暗,雷達角分辨率低,GPS在隧道中失效,IMU積分會漂移。
此時,濾波器的角色從"清潔工"升級為**“融合大師”**。它利用數學工具,在不確定性中構建對世界最可能的認知。
核心應用場景:
- 環境感知與目標跟蹤:使用KF/EKF預測動態目標軌跡,維持ID連續性。
- 高精度定位:通過EKF/UKF融合RTK-GPS、IMU、輪速計,實現厘米級定位。
- 車輛狀態估計:用EKF估計側滑角、真實速度;用互補濾波分離重力分量。
本質:這一境界的濾波器,是系統的"小腦",負責協調多源信息,生成連貫、可靠的狀態估計,為決策提供堅實基礎。
第三重境界:抉擇——測試中的雙刃劍
在自動駕駛的研發閉環中,測試驗證是確保安全的最終防線。然而,測試工程師面臨一個悖論:原始數據充滿噪聲,難以分析;但濾波處理又可能扭曲事實,掩蓋問題。
濾波器在此刻成為一把"雙刃劍":
- 用得好:它是"數據醫生",能生成高精度真值、準確評估性能、輔助故障診斷。
- 用得不好:它是"遮羞布",可能抹平緊急制動的峰值、掩蓋傳感器的周期性抖動,讓測試結果失去意義。
如何科學選擇濾波器?——場景化決策指南
選擇濾波器必須基于明確的測試目標。以下是常見測試場景下的推薦策略:
| 測試目標 | 關鍵分析需求 | 推薦濾波器 | 參數建議與注意事項 |
|---|---|---|---|
| AEB/FCW功能觸發評估 | 精確的相對距離、相對速度變化率,捕捉瞬時事件。 | 輕度一階低通 或 零相位低通 | 截止頻率:10-20 Hz。 禁止重度濾波!需保留剎車尖峰。建議同時展示原始與濾波后信號對比。 |
| 乘坐舒適性分析 (Ride Comfort) | 人體感知的低頻晃動(點頭、俯仰、橫擺),抑制高頻路面噪聲。 | 中度一階低通 或 帶阻濾波器 | 截止頻率:3-5 Hz。 若存在明顯發動機共振(如30Hz),使用帶阻濾波器精準切除。 |
| 高精度軌跡生成 (Ground Truth) | 厘米級絕對位置、速度、姿態,長期穩定性。 | 擴展卡爾曼濾波器 (EKF) | 必須融合RTK-GPS、高精度IMU、輪速計。 仔細標定噪聲協方差 Q\mathbf{Q}Q 和 R\mathbf{R}R。 |
| 能耗與續航測試 | 平均加速度、宏觀速度曲線,對瞬時抖動不敏感。 | 重度一階低通 或 移動平均 | 截止頻率:1-2 Hz 或 N=50-100 的移動平均。 目標是得到平滑的宏觀趨勢。 |
| 傳感器故障診斷 | 分析原始噪聲的頻譜、方差、周期性,定位干擾源。 | 禁止濾波 | 必須使用原始信號進行FFT頻譜分析、統計分析。 濾波會"擦除"故障證據。 |
| 規劃控制算法驗證 | 平滑的車輛狀態輸入,避免控制器因噪聲抖動。 | 實時一階低通 或 EKF | 截止頻率:5-10 Hz。 注意相位延遲對控制的影響,必要時進行延遲補償。 |
| 仿真場景復現 (HIL/SIL) | 提供穩定、合理的車輛狀態給仿真平臺。 | 零相位濾波 (離線) 或 EKF (實時) | 離線分析用 filtfilt 消除相位延遲。確保虛擬傳感器輸入的合理性。 |
黃金法則:
- 目標驅動:先問"為什么濾波",再決定"怎么濾"。
- 保留原始數據:原始數據是"法律證據",永遠不要丟棄。
- 透明公開:在報告中明確標注:濾波器類型、截止頻率、階數、是否零相位、實現庫(如
scipy.signal)。- 驗證對比:始終進行"濾波前后"對比,檢查是否引入虛假特征或丟失關鍵信息。
結語:濾波器即哲學
濾波器的故事,遠不止于數學公式。它體現了工程實踐中最深刻的哲學——在噪聲與真實、平滑與細節、效率與準確之間尋求平衡。
在自動駕駛這條充滿不確定性的道路上,濾波器教會我們:真正的智能,不在于擁有完美的數據,而在于如何在不完美的世界中,做出最優的估計與決策。
當你下次看到一條平滑的車輛軌跡曲線時,請記住,那不僅是技術的勝利,更是無數工程師在"濾波"二字上反復權衡、嚴謹求證的結果。因為在這里,一個小小的截止頻率,可能就決定了安全與危險的距離。
— by AGI 本文部分內容由通義千問生成整理匯總,僅供入門參考。歡迎學習交流!
參考文獻
[1] Euro NCAP. (2022). Test Protocol Bulletin TB021: Data Acquisition and Injury Calculation (Version 4.1). Euro NCAP Technical Report. Retrieved from https://www.euroncap.com/media/79880/tb-021-data-acquisition-and-injury-calculation-v41.pdf
附錄
文首的測試demo
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from scipy.signal import butter, filtfiltdef butter_lowpass_filter(data, cutoff, fs, order=4):"""Apply Butterworth lowpass filterParameters:data : array_like - Input datacutoff : float - Cutoff frequency (Hz)fs : float - Sampling frequency (Hz)order : int - Filter orderReturns:y : array_like - Filtered data"""nyquist = 0.5 * fsnormal_cutoff = cutoff / nyquistb, a = butter(order, normal_cutoff, btype='low', analog=False)y = filtfilt(b, a, data)return y# Parameter settings
duration = 20 # Duration (seconds)
fs = 100 # Sampling frequency (Hz)
cutoff_freq_05 = 0.5 # Original cutoff frequency (Hz)
cutoff_freq_2 = 2.0 # New 2Hz cutoff frequency (Hz)
cutoff_freq_5 = 5.0 # New 5Hz cutoff frequency (Hz)
cutoff_freq_10 = 10.0 # New 10Hz cutoff frequency (Hz)
filter_order = 4 # Standard filter order
filter_order_12 = 4 # Standard filter order# Generate time axis
t = np.linspace(0, duration, int(fs * duration), endpoint=False)# Simulate lateral acceleration data (including multiple frequency components and noise)
# Low frequency components (real lateral acceleration changes)
true_acceleration = 2 * np.sin(2 * np.pi * 0.1 * t) + 1.5 * np.sin(2 * np.pi * 0.3 * t)# Additional components at 2Hz and 5Hz
additional_components = 0.8 * np.sin(2 * np.pi * 2 * t) + 0.6 * np.sin(2 * np.pi * 5 * t)# High frequency noise
noise = 0.5 * np.random.normal(0, 1, len(t)) + 0.3 * np.sin(2 * np.pi * 5 * t) + 0.2 * np.sin(2 * np.pi * 15 * t)# Original measurement data (real signal + additional components + noise)
raw_acceleration = true_acceleration + additional_components + noise# Apply Butterworth lowpass filters with different cutoff frequencies
filtered_acceleration_05 = butter_lowpass_filter(raw_acceleration, cutoff_freq_05, fs, filter_order)
filtered_acceleration_2 = butter_lowpass_filter(raw_acceleration, cutoff_freq_2, fs, filter_order)
filtered_acceleration_5 = butter_lowpass_filter(raw_acceleration, cutoff_freq_5, fs, filter_order)
filtered_acceleration_10 = butter_lowpass_filter(raw_acceleration, cutoff_freq_10, fs, filter_order_12)# Create separate plots for each filter
plt.figure(figsize=(15, 15))# Plot 1: Original data
plt.subplot(3, 3, 1)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, label='Raw Data')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s2)')
plt.title('Original Lateral Acceleration Data')
plt.grid(True, alpha=0.3)
plt.legend()# Plot 2: 0.5Hz filter
plt.subplot(3, 3, 2)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, alpha=0.3, label='Raw Data')
plt.plot(t, filtered_acceleration_05, 'r-', linewidth=1.5,label=f'Butterworth LPF ({cutoff_freq_05} Hz, Order {filter_order})')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s2)')
plt.title('0.5Hz Lowpass Filter')
plt.grid(True, alpha=0.3)
plt.legend()# Plot 3: 2Hz filter
plt.subplot(3, 3, 3)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, alpha=0.3, label='Raw Data')
plt.plot(t, filtered_acceleration_2, 'g-', linewidth=1.5,label=f'Butterworth LPF ({cutoff_freq_2} Hz, Order {filter_order})')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s2)')
plt.title('2Hz Lowpass Filter')
plt.grid(True, alpha=0.3)
plt.legend()# Plot 4: 5Hz filter
plt.subplot(3, 3, 4)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, alpha=0.3, label='Raw Data')
plt.plot(t, filtered_acceleration_5, 'm-', linewidth=1.5,label=f'Butterworth LPF ({cutoff_freq_5} Hz, Order {filter_order})')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s2)')
plt.title('5Hz Lowpass Filter')
plt.grid(True, alpha=0.3)
plt.legend()# Plot 5: 10Hz filter (12th order)
plt.subplot(3, 3, 5)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, alpha=0.3, label='Raw Data')
plt.plot(t, filtered_acceleration_10, 'c-', linewidth=1.5,label=f'Butterworth LPF ({cutoff_freq_10} Hz, Order {filter_order_12})')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s2)')
plt.title('10Hz Lowpass Filter (12th Order)')
plt.grid(True, alpha=0.3)
plt.legend()# Plot 6: Combined comparison of all filters
plt.subplot(3, 3, 6)
plt.plot(t, raw_acceleration, 'b-', linewidth=0.8, alpha=0.3, label='Raw Data')
plt.plot(t, filtered_acceleration_05, 'r-', linewidth=1.5,label=f'LPF ({cutoff_freq_05} Hz, Order {filter_order})')
plt.plot(t, filtered_acceleration_2, 'g-', linewidth=1.5,label=f'LPF ({cutoff_freq_2} Hz, Order {filter_order})')
plt.plot(t, filtered_acceleration_5, 'm-', linewidth=1.5,label=f'LPF ({cutoff_freq_5} Hz, Order {filter_order})')
plt.plot(t, filtered_acceleration_10, 'c-', linewidth=1.5,label=f'LPF ({cutoff_freq_10} Hz, Order {filter_order_12})')
plt.xlabel('Time (s)')
plt.ylabel('Lateral Acceleration (m/s2)')
plt.title('Combined View: All Filters Comparison')
plt.grid(True, alpha=0.3)
plt.legend()# 調整布局,增加上下部分之間的間距
plt.tight_layout(pad=3.0, h_pad=3.0, w_pad=1.0)
plt.show()# Print filter information
print(f"Sampling Frequency: {fs} Hz")
print(f"Standard Filter Order: {filter_order}")
print(f"10Hz Filter Order: {filter_order_12}")
print(f"Number of Data Points: {len(t)}")
print(f"Data Duration: {duration} s")
print("\nApplied Filters:")
print(f" - Lowpass Filter 1: {cutoff_freq_05} Hz (Order {filter_order})")
print(f" - Lowpass Filter 2: {cutoff_freq_2} Hz (Order {filter_order})")
print(f" - Lowpass Filter 3: {cutoff_freq_5} Hz (Order {filter_order})")
print(f" - Lowpass Filter 4: {cutoff_freq_10} Hz (Order {filter_order_12})")



















