【題目鏈接】

ybt 1552：【例 1】點的距離

【題目考點】

1. 最近公共祖先（LCA）：倍增求LCA

知識點講解見：洛谷 P3379 【模板】最近公共祖先（LCA）

【解題思路】

首先用鄰接表保存輸入的無權圖。
使用倍增求LCA的解題方法：設dep數組，$de{p}_u$表示頂點u的深度。設fa數組，$f{a}_{i,j}$表示從結點i開始向上走$2^j$步可以到達的結點。
而后對該圖做深度優先遍歷，可以預處理求出dep數組和fa數組，同時也將該圖變為了有根樹。
該圖是無權圖，可以認為每條邊長度為1。
無權有根樹上，根結點到一個結點的路徑長度為該結點的深度（根結點深度為0）。
樹上任意兩結點之間存在唯一的路徑。記結點x到結點y的路徑長度為$Dis(x,y)$。
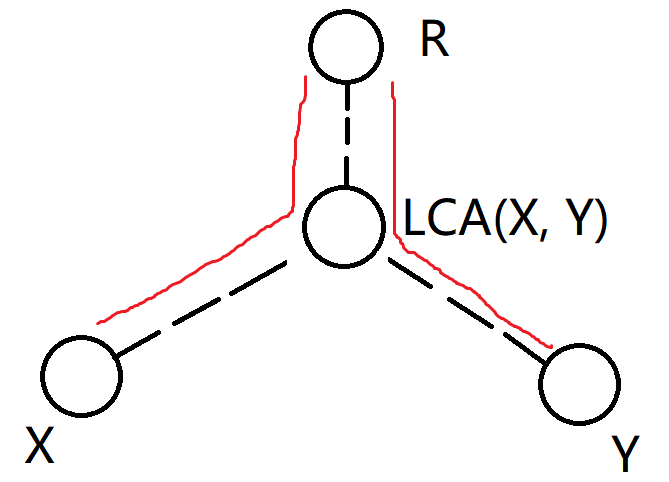
結點x到結點y的路徑必然經過二者的最近公共祖先LCA(x, y)。
已知根結點r到x的路徑長度為$dep[x]$，根結點r到y的路徑長度為$dep[y]$。
根結點r到x的路徑可以分為r到LCA(x,y)的路徑，以及LCA(x, y)到x的路徑。
根結點r到y的路徑可以分為r到LCA(x,y)的路徑，以及LCA(x, y)到y的路徑。
二者相加后，總長度包括x到LCA(x, y)的路徑長度，LCA(x, y)到y的路徑長度，以及兩倍的r到LCA(x, y)的路徑長度。即x到y的路徑長度加上兩倍的LCA(x, y)的深度。
因此$dep[x]+dep[y]=Dis(x,y)+2dep[LCA(x,y)]$
所以$Dis(x,y)=dep[x]+dep[y]?2dep[LCA(x,y)]$

使用倍增求LCA算法，每次查詢$Dis(x,y)$的時間復雜度為$O(\log n)$

【題解代碼】

• 解法1：倍增求LCA

#include<bits/stdc++.h>
using namespace std;
#define N 100005
#define LN 25
vector<int> edge[N];
int n, lg[N], dep[N], fa[N][LN];//f[i][j]：頂點i向上走2^j到達的頂點 
void initLg()
{for(int i = 2; i <= n; ++i)lg[i] = lg[i/2]+1;
}
void dfs(int u)
{for(int v : edge[u]) if(v != fa[u][0])//v不是u的父親 {fa[v][0] = u;dep[v] = dep[u]+1;for(int j = 1; 1<<j <= dep[v]; ++j)fa[v][j] = fa[fa[v][j-1]][j-1];dfs(v);}
}
int lca(int u, int v)
{if(dep[u] < dep[v])swap(u, v);while(dep[u] > dep[v])u = fa[u][lg[dep[u]-dep[v]]];if(u == v)//如果v本身為LCA(u, v)，那么當二者深度相同時，二者相同 return u;for(int k = lg[dep[u]]; k >= 0; --k)if(fa[u][k] != fa[v][k])u = fa[u][k], v = fa[v][k];return fa[u][0];
}
int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int q, x, y;cin >> n;for(int i = 1; i < n; ++i){cin >> x >> y;edge[x].push_back(y);edge[y].push_back(x);}initLg();dfs(1);cin >> q;while(q--){cin >> x >> y;cout << dep[x]+dep[y]-2*dep[lca(x, y)] << '\n';}return 0;
}