https://www.lamda.nju.edu.cn/chengq/optfall24/slides/Lecture_9.pdf
目錄
關于對偶的一些解釋
1. Max-min characterization 最大最小準則
2. Saddle-point Interpretation 鞍點解釋
3. Game interpretation 博弈論里的對偶
Optimality Conditions 最優條件
1. Certificate of Suboptimality and Stopping Criteria?次優性證明與停止準則
2. Complementary Slackness 互補松弛性
3. KKT Optimality Conditions
Ex.1
Ex.2
4. Solving the Primal Problem via the Dual 通過對偶解原問題
例1. Entropy Maximization 最大熵問題
例2. 等式約束與函數分配
5. Examples
5.1 引入新變量及相關等式約束
5.1.1 Unconstrained geometric program
5.1.2? Norm approximation problem
5.1.3不等式約束的幾何規劃
5.2 原目標函數的轉換
5.3顯式約束隱式化 納入目標函數的定義域
6. Generalized inequalities 廣義不等式
Ex.1
Ex.2
關于對偶的一些解釋
1. Max-min characterization 最大最小準則
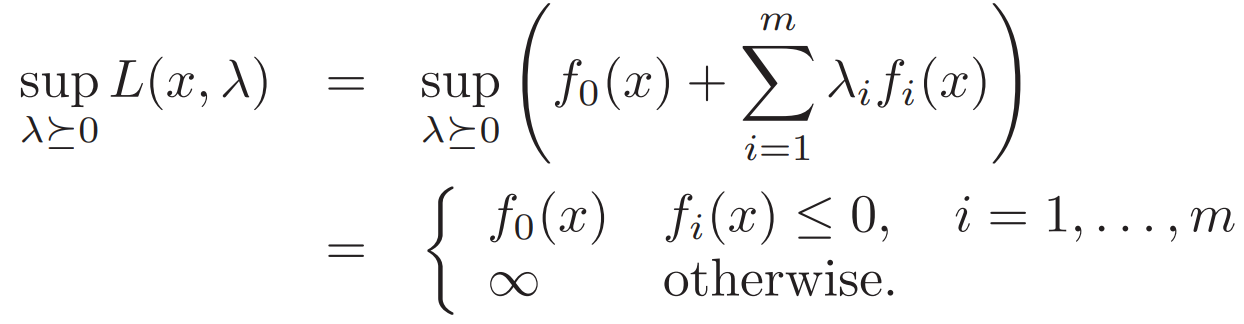
如果有f＞0 選取無窮大λ 上界就達到無窮； 如果所有 f≤0 取λ=0 結果即為f0
原問題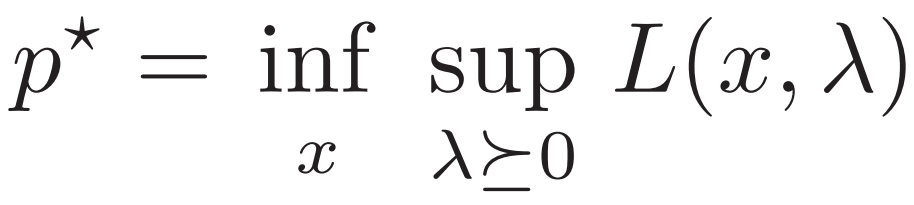
? 對偶問題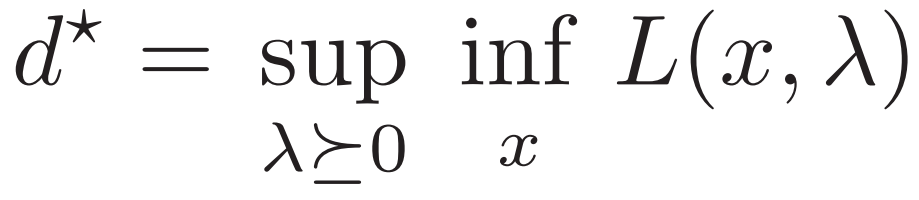
代入這兩個 p*為上界的下界 以及 d*為下界的上界 可重寫強弱對偶
2. Saddle-point Interpretation 鞍點解釋
3. Game interpretation 博弈論里的對偶
玩家1選擇w? 玩家2 選擇z? 玩家1向玩家2支付
?因此1想最小化? ?2想最大化
若玩家1先選 會預判到 玩家2會選擇他選后的最優 即為上界
所以玩家1會選
?交易為
若玩家2先手 則交易為
這個問題中 同一玩家 先動時一定比后動時收益更高，最優對偶的間隙gap即為先動優勢。
但如果鞍點存在，先后動的最優一致，均為鞍點處。
回到之前的拉格朗日問題 即為玩家1選x 玩家2選λ，最優的x*對應p* 最優的λ*對應d*。
Optimality Conditions 最優條件
1. Certificate of Suboptimality and Stopping Criteria?次優性證明與停止準則
如果能找到一個原問題的可行解f0(x) 對偶問題的可行解g(λ,v)? ?可框定范圍 g(λ,v) ≤ d *≤ p* ≤ f0(x)
可在迭代k次后 計算一下對偶間距 絕對誤差 相對誤差，幫助確定迭代的終止條件
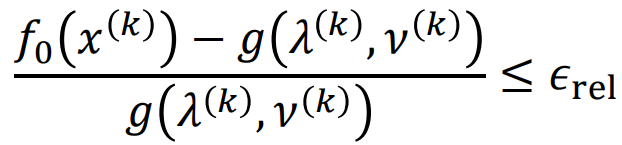
2. Complementary Slackness 互補松弛性
強對偶成立時 原問題對偶問題最優值相等 下面兩個≤ 都得取等
需要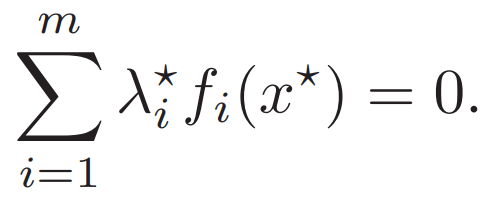
?由于每一項≤0? 也就需要每個都=0?
也就有互補松弛性 其中一個>0 則有另一個=0
? ? ?
3. KKT Optimality Conditions
KKT條件是 非凸優化的必要條件（可推出）? ? 特別地，是凸優化的充要條件
對于對偶間距為0的強對偶問題 若最優點為?
?偏導數為0
可行條件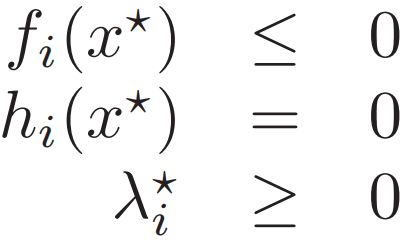
? ? ?對偶條件
總偏導數為0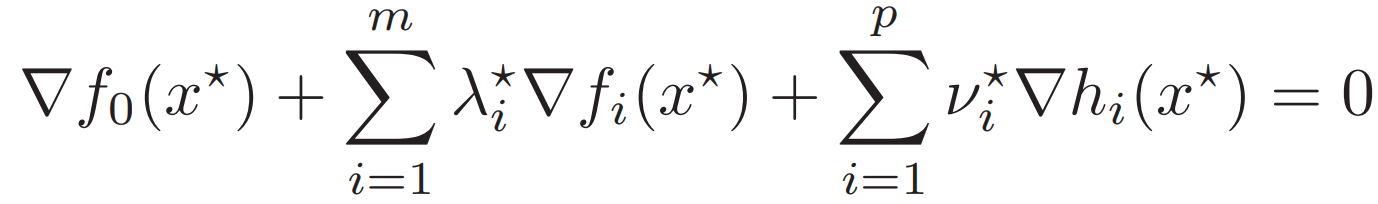
為什么對于凸優化充分：
對于凸優化而言，f是凸函數 h是仿射函數 偏導為0就可推出 L是全局最小值
對于一般優化 KKT（偏導為0）是MIN 的必要條件 ； 凸優化 KKT <=> MIN
Ex.1
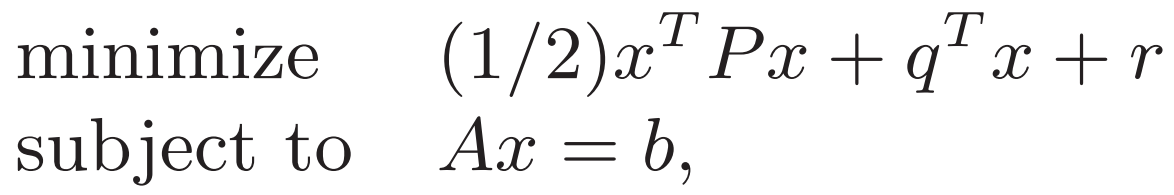
是凸優化 因為沒有不等式約束 KKT只有等式約束和偏導=0 兩個條件
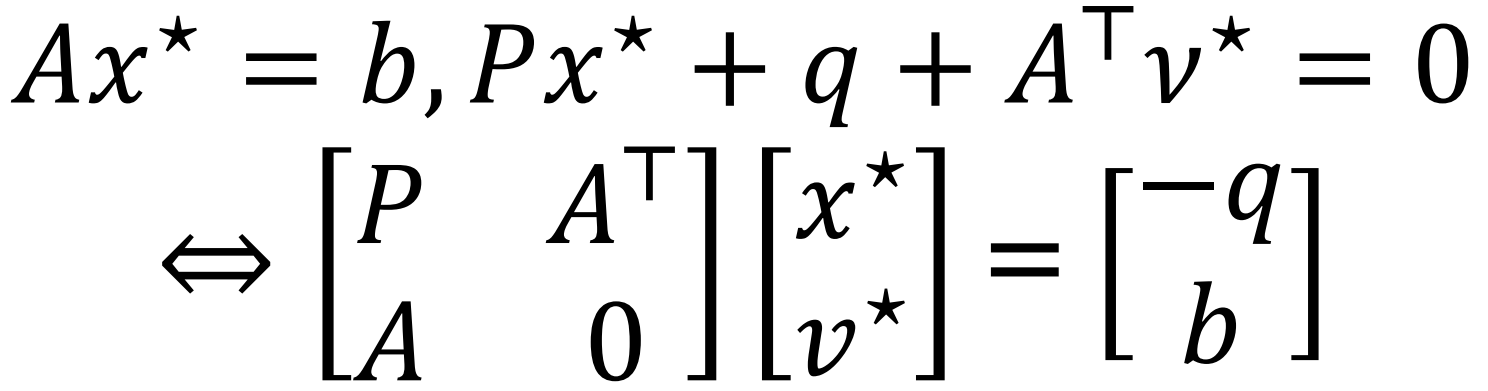
Ex.2
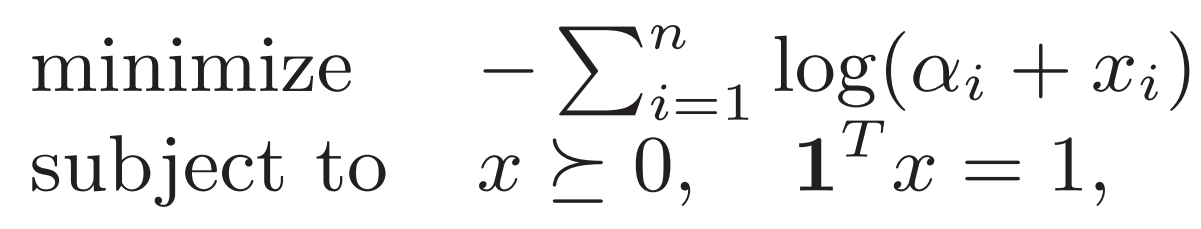
列出KKT條件 三個原先 一個對偶 一個總偏導
? 用其他量表示λ 消去λ
?????
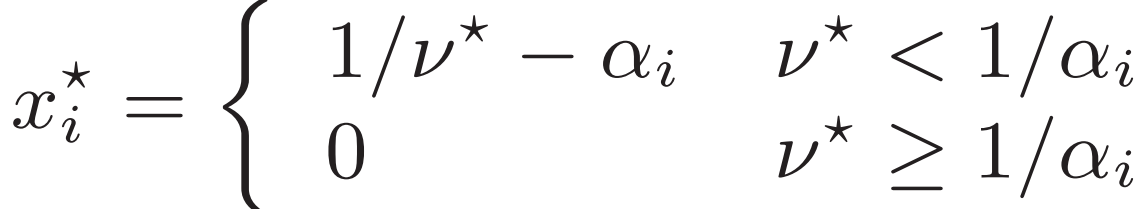
因為x*求和為1 就像把1體積的水倒入 底部高度為αi的容器 水位在1/v*
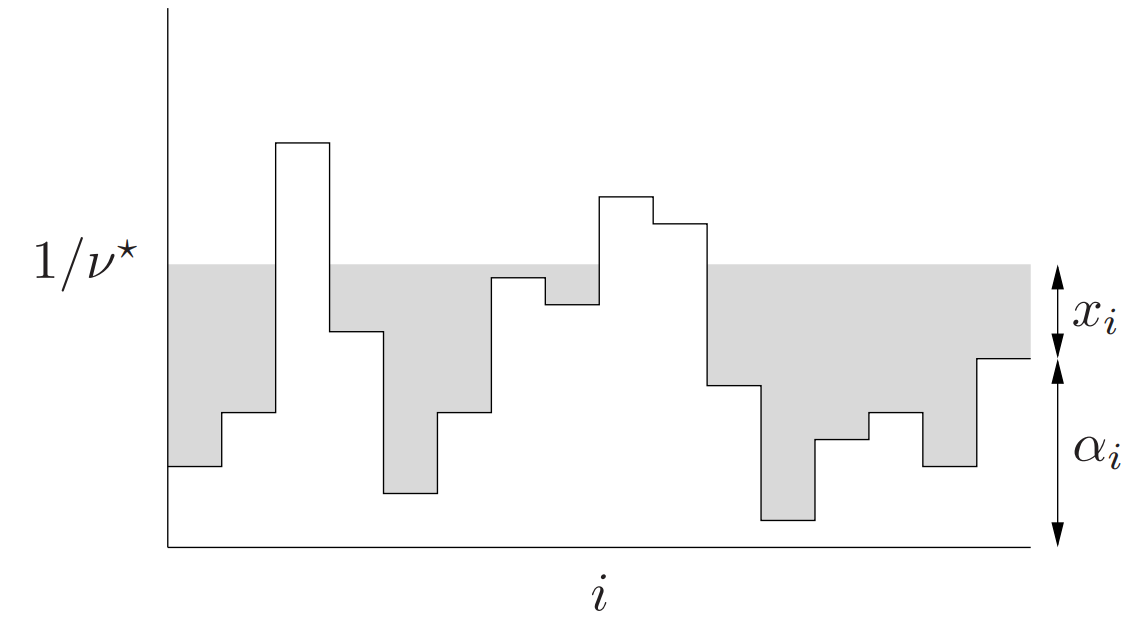
如果不用凸優化 偏導為
?越小降低空間越大
每次調高偏導最小的x 最后結果即確定一個閾值（水位）閾值以下的
加到閾值
4. Solving the Primal Problem via the Dual 通過對偶解原問題
若對偶最優解(λ*,v*)存在，對應到 min L(x,λ*,v*)? ? ? ?λ v先確定的前提下 x對應使L最小的取值
原問題可行，則對偶問題有最優解； 原問題無可行解，則對偶問題無界
四步：1.寫出對偶問題? 2.slater條件 是否強對偶? 3.求解對偶問題? 4.KKT 對偶問題對應原問題
例1. Entropy Maximization 最大熵問題
?NJU 凸優化導論(8) Lagrange Dual 拉格朗日對偶-CSDN博客
之前在共軛函數 slater條件那里 兩次提過這個例子（附近的知識點遺忘可以點上面鏈接復習一下）
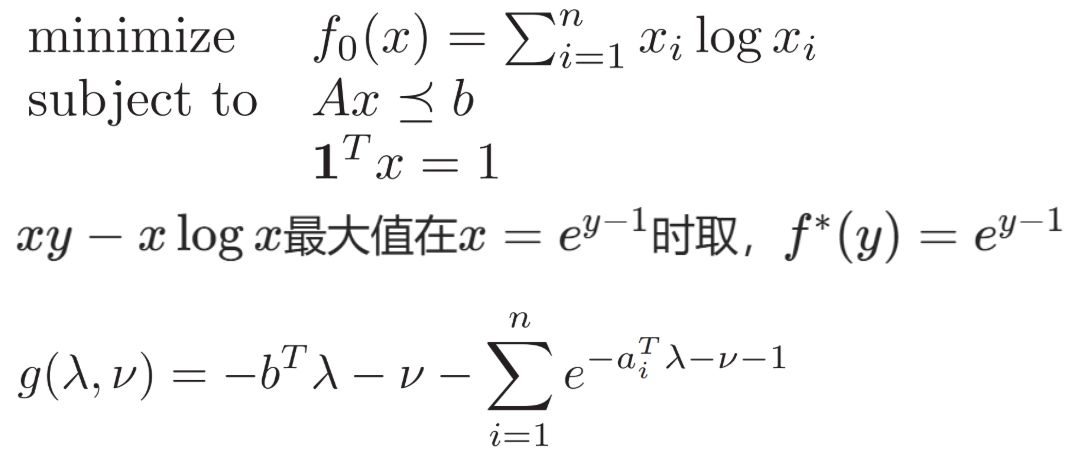
滿足弱版本的slater條件 不等式為仿射函數
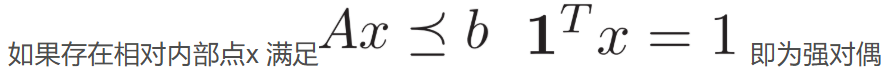
求解對偶問題：對偶問題對v求導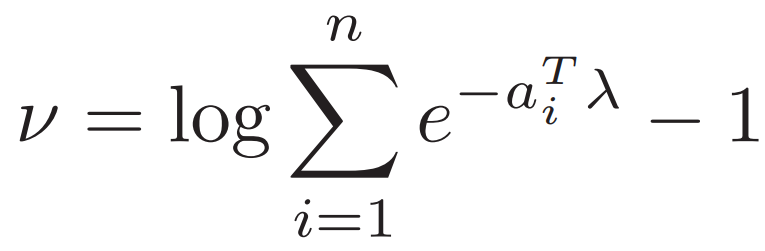
?再代入對偶問題
?
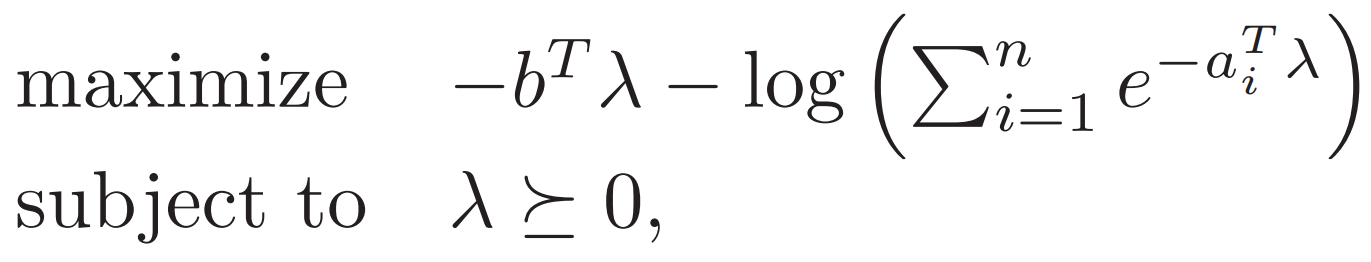
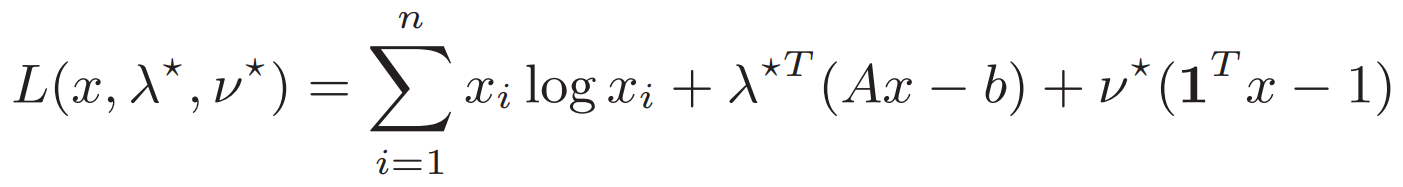
求解λ和v之后帶入得x??
?
例2. 等式約束與函數分配
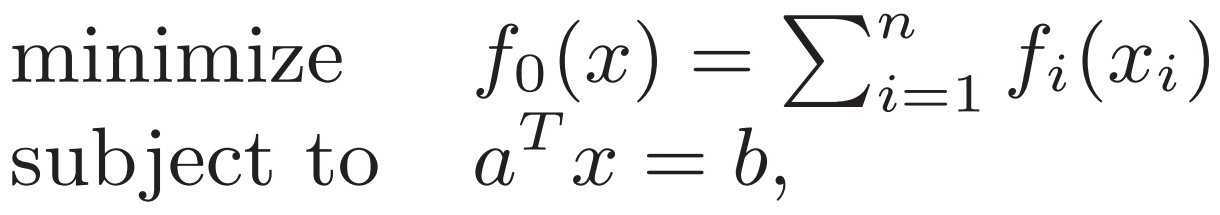
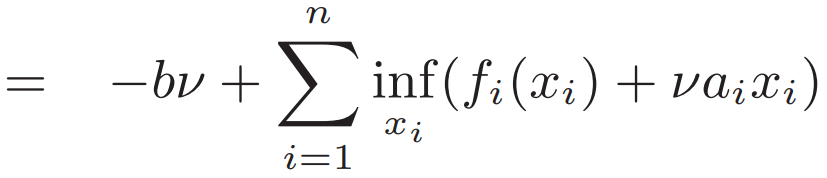
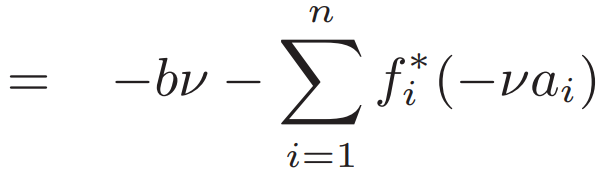
求解對偶函數得到v*
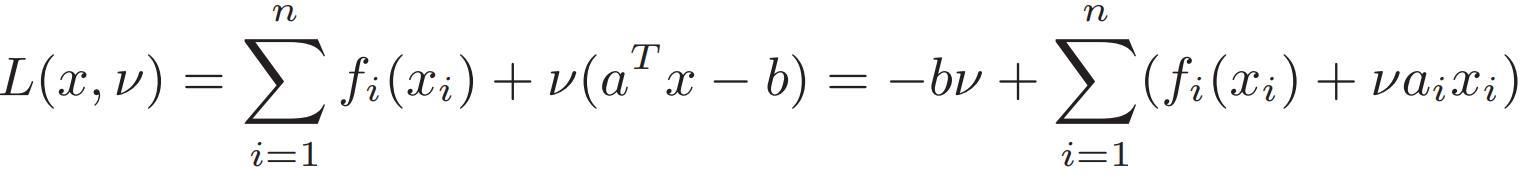
若f都是凸函數 則L也是凸函數 則目標x要最小化L? L對x求偏導 得x*與v*的關系
5. 變形重構原問題 轉換對偶
通過示例說明，對一個問題進行簡單的等價重構，可能會得到截然不同的對偶問題
5.1 引入新變量及相關等式約束
? 沒約束 寫拉格朗日還是本身
由原來的無約束 添加變量寫成有等式約束
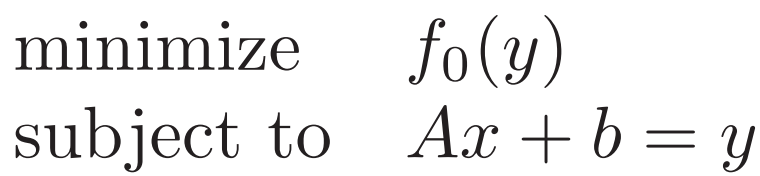? ? 拉格朗日形式為
?
否則下界就負無窮
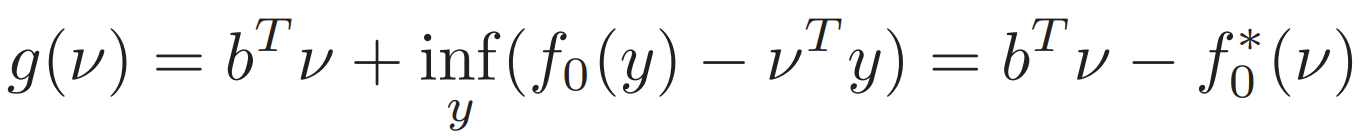
所以總的對偶問題可以寫成?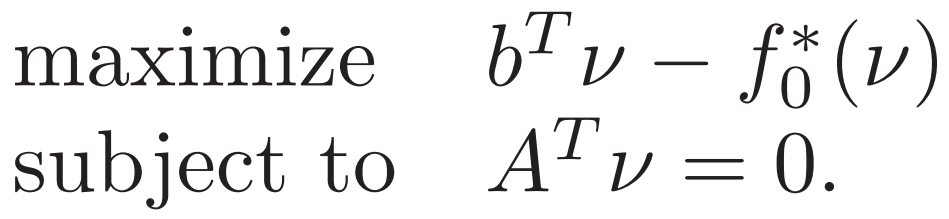
5.1.1 Unconstrained geometric program
?原問題添加變量寫成
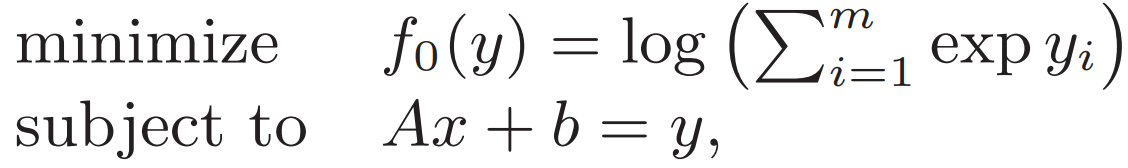
對共軛形式求偏導?且要滿足條件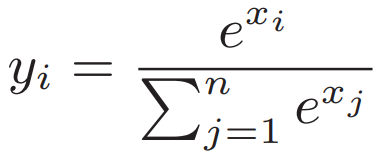
?
?
用v消去y得到共軛函數? ?把共軛函數和條件對應定義域? 得到對偶問題
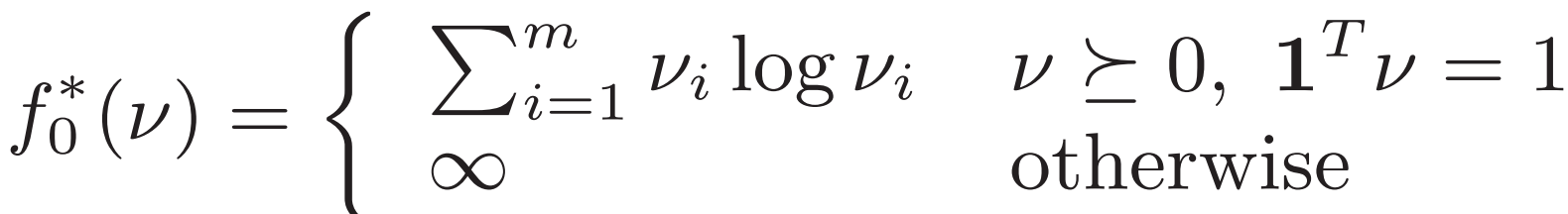
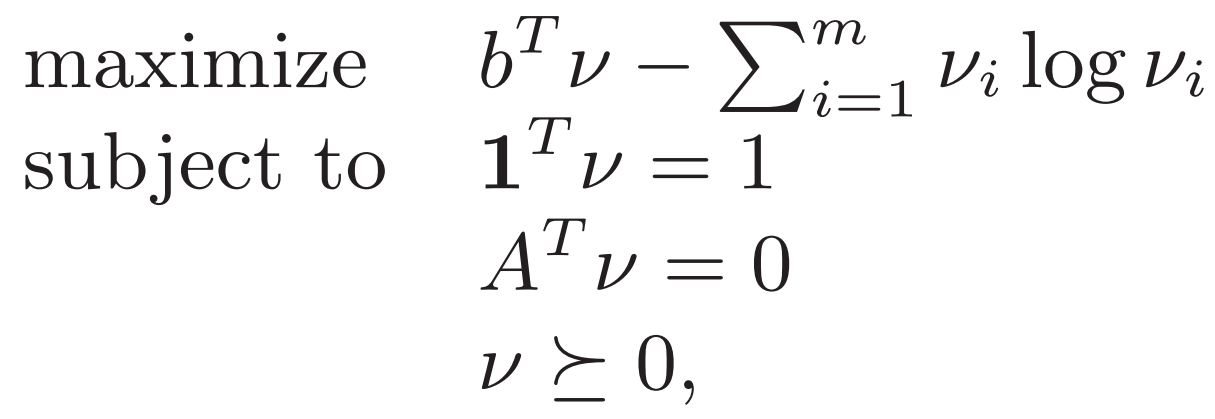
5.1.2? Norm approximation problem
?把仿射拿出來 改寫成
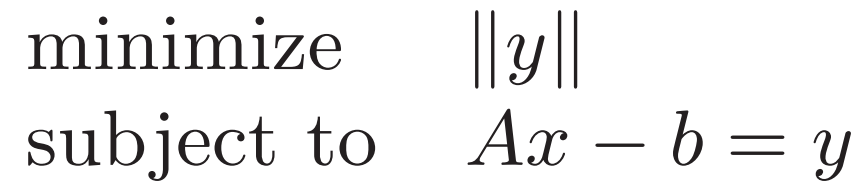
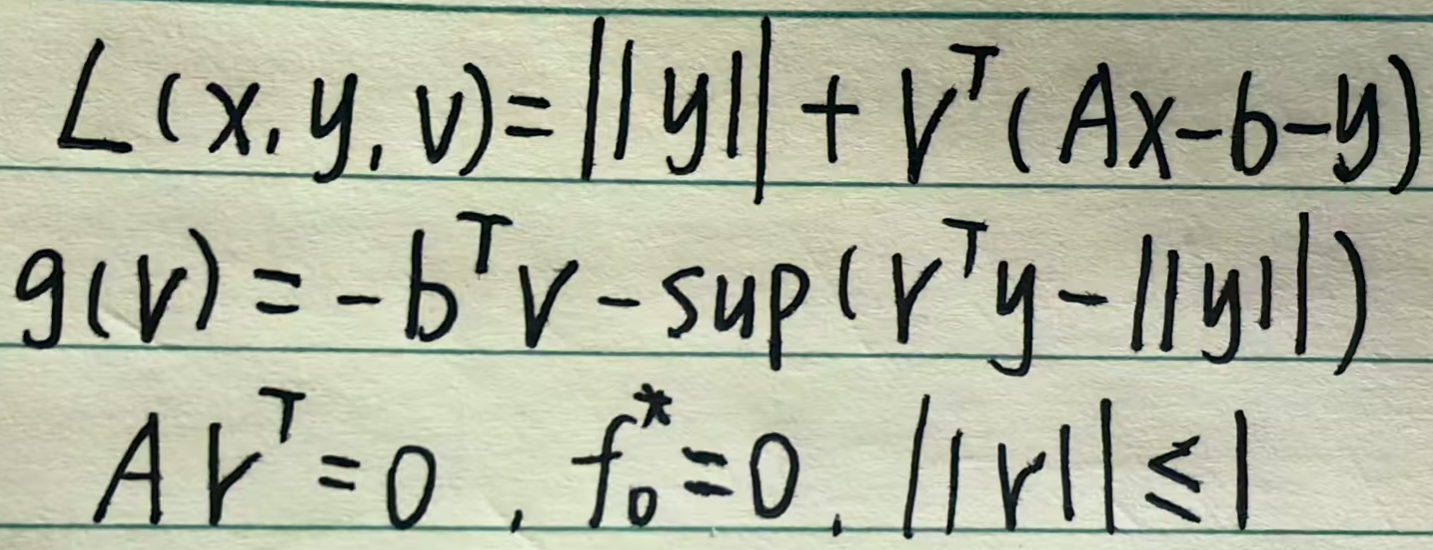?代入范數的共軛得
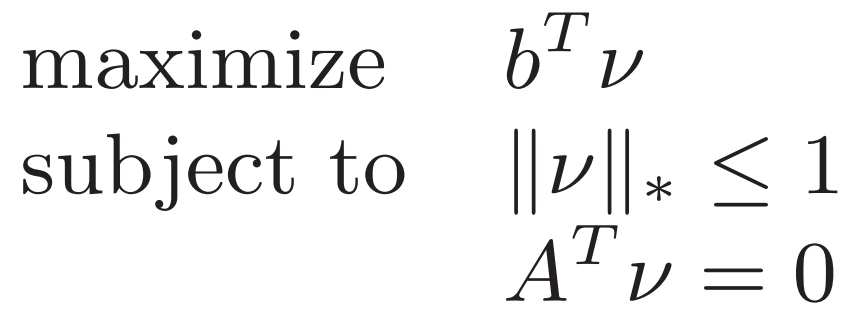
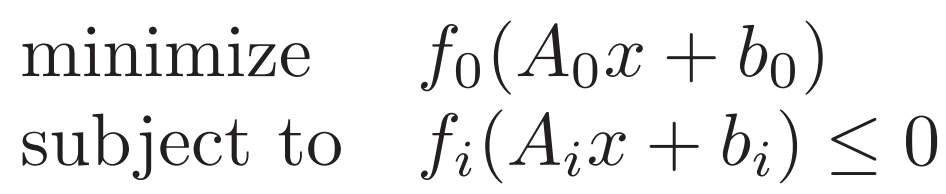仿射套函數 可改寫為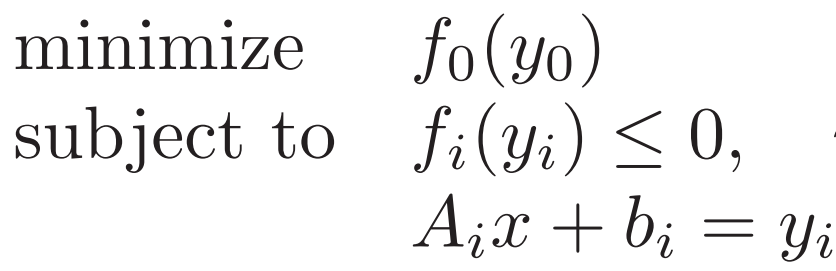
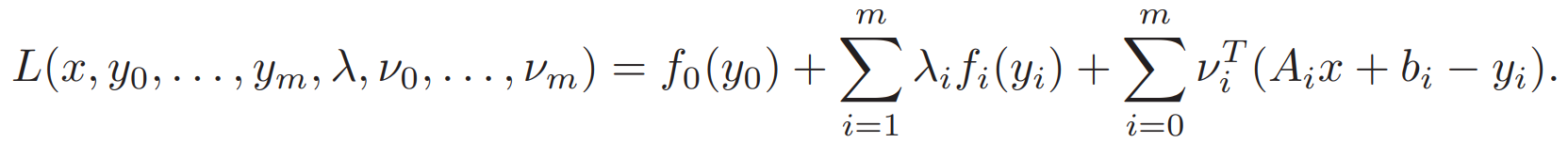
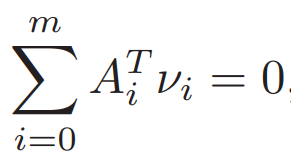?否則x就可以使L到無窮小? ?每個f都寫成共軛
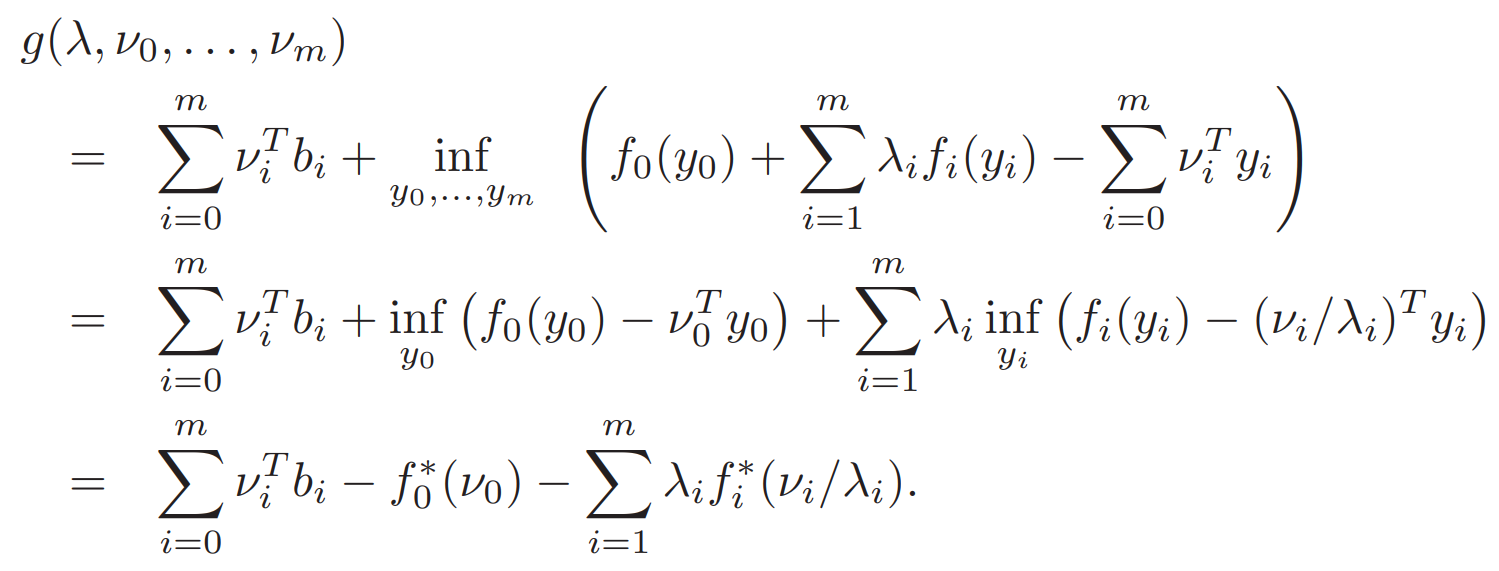
故可以寫作
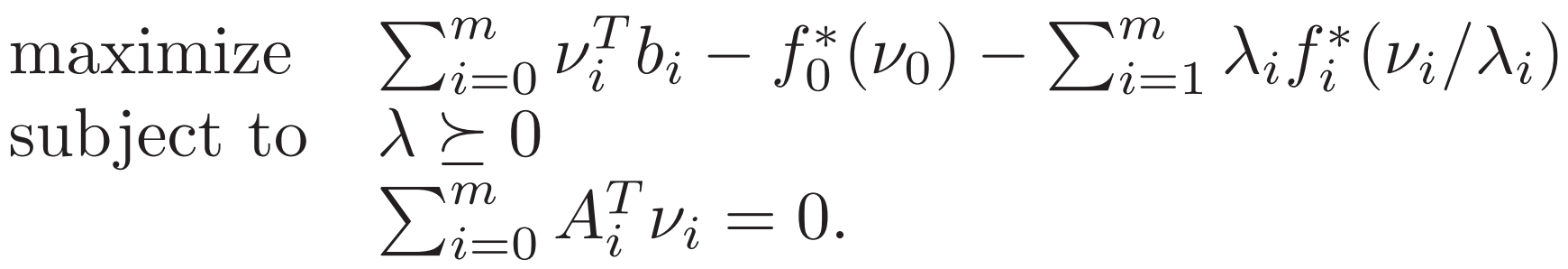
5.1.3不等式約束的幾何規劃
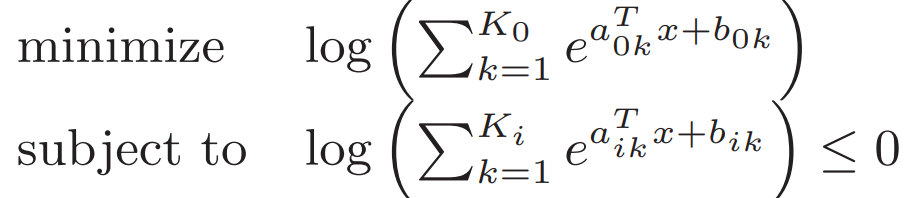
我們
? ?就變成
?可代入上模版
利用這個 指數求和對數 exp-sum-log 的共軛
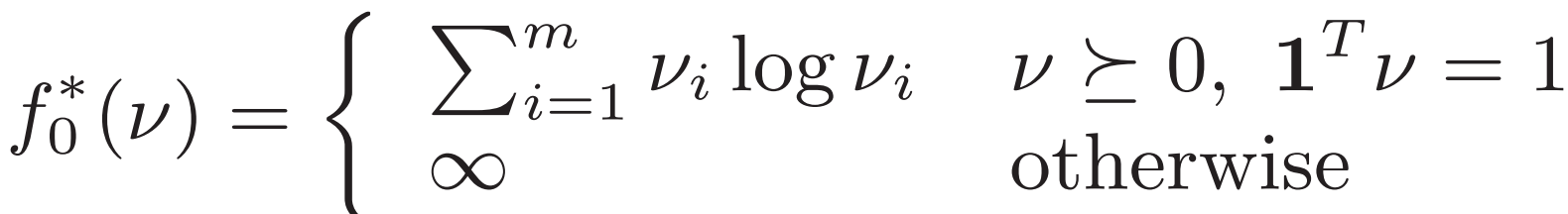
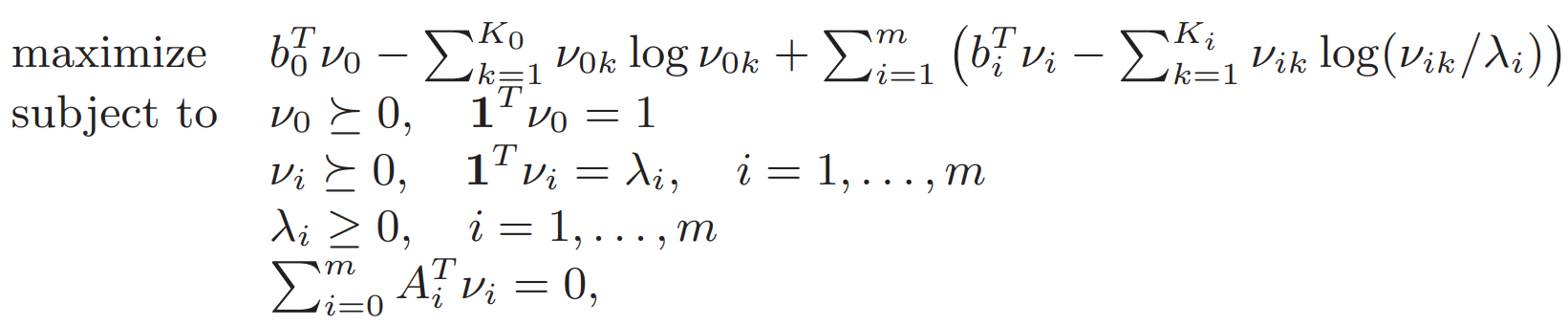
5.2 原目標函數的轉換
把原問題的f0 用一個遞增函數替換 使得結果不變 但使得對偶問題更好
一個方式的范數變換 是之前上面的 5.1.2 Norm approximation problem? 但我們還可以
?把二范數平方/2 使得更好求導
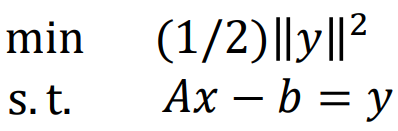
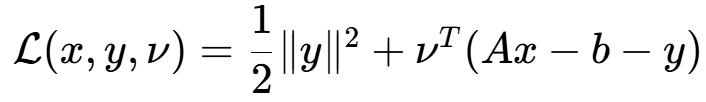
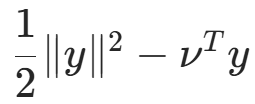?對y偏導得?
最后的對偶問題為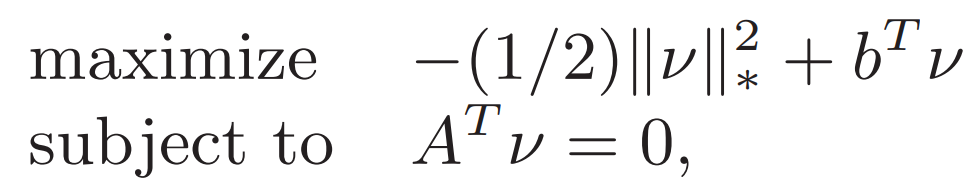
5.3顯式約束隱式化 納入目標函數的定義域
?
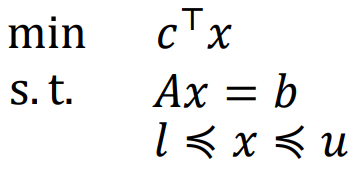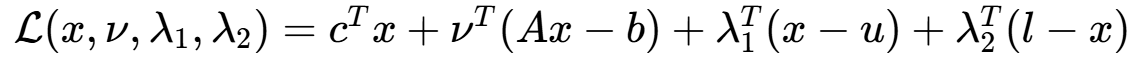
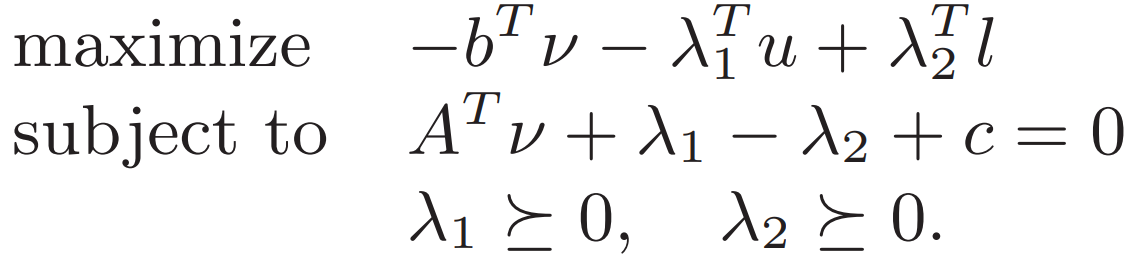
如果改寫 把盒形約束放到 f0 中
? ? ???
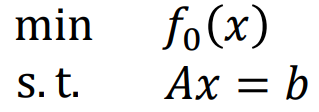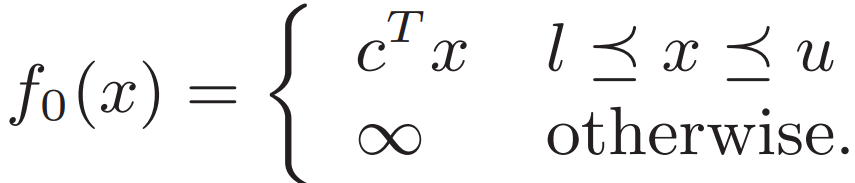
v前的系數為 Av+c 因為要最小化 對于每個x 如果系數為正就取l 為負就取u
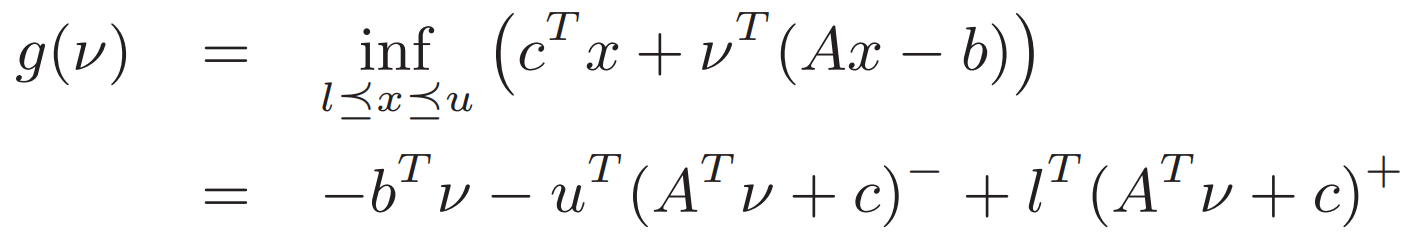
好處是 這個對偶最后是一個無約束問題
6. Generalized inequalities 廣義不等式
? ?? ?
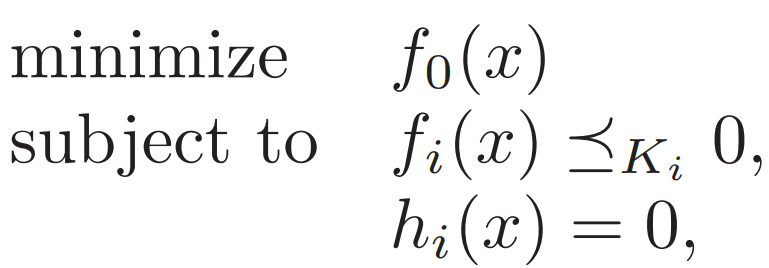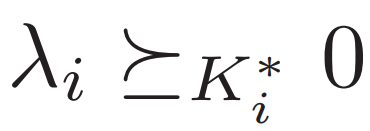
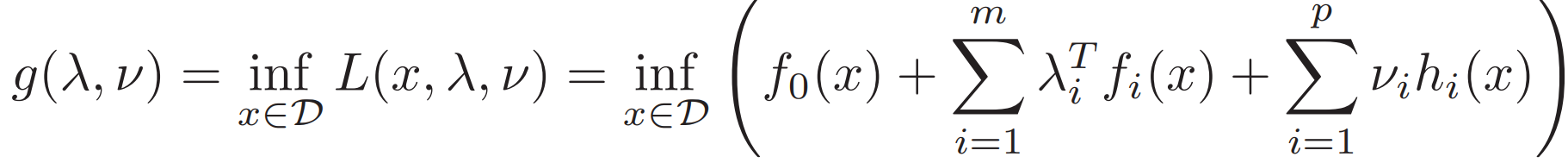
廣義的Slater條件 換成廣義小于
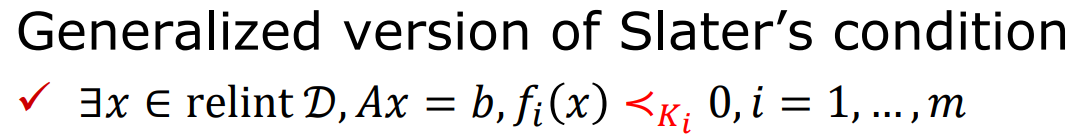
Ex.1
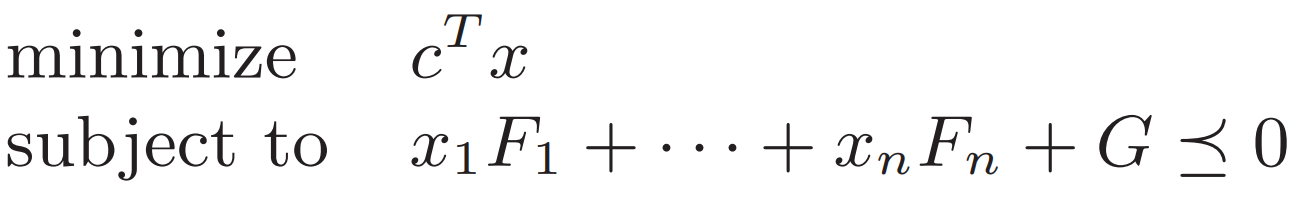
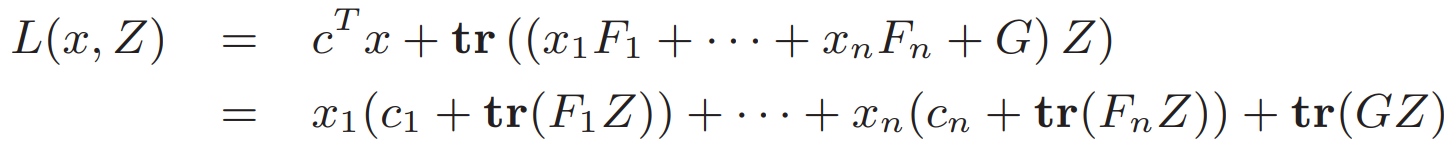
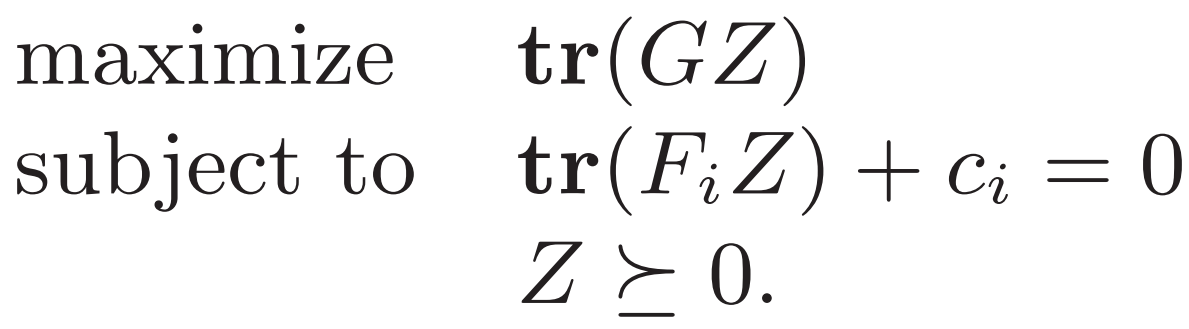
Ex.2
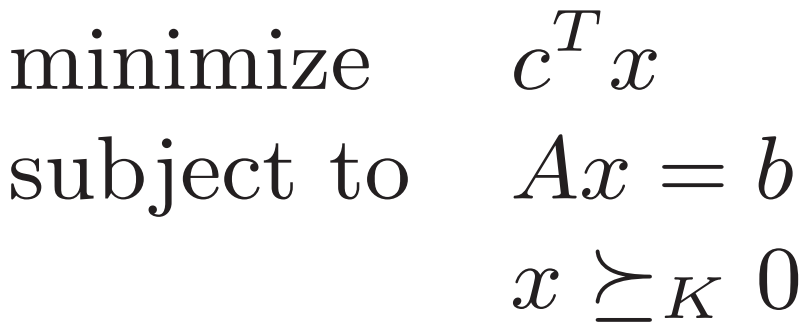
Slater條件?
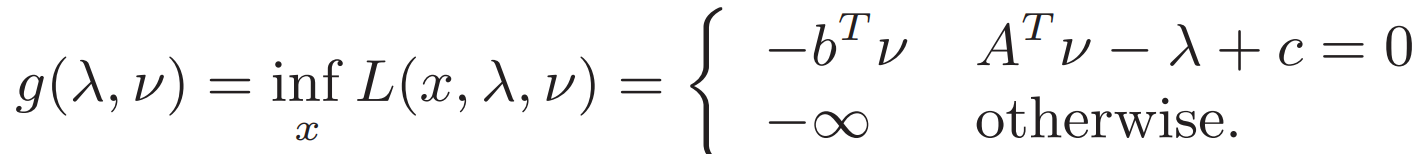
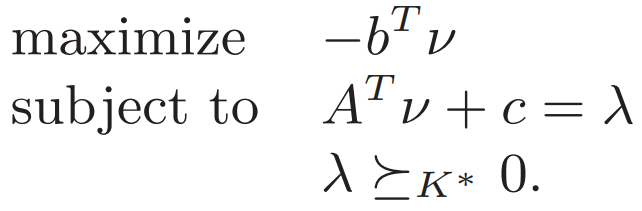? ?? 消掉λ 再代入
得
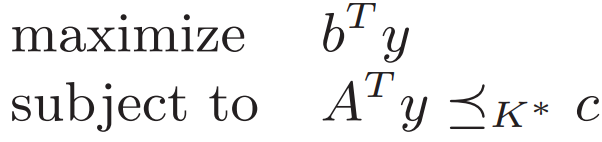
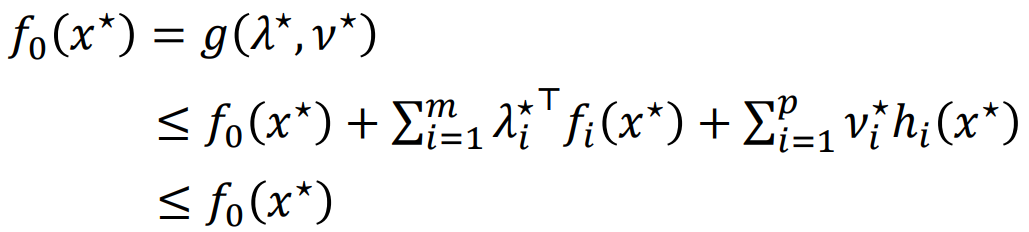
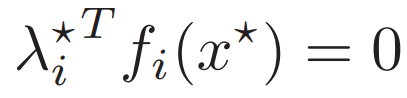同樣具有互補松弛性
同樣的 Slater條件、KKT條件、互補松弛性 只是把不等式改成廣義不等式
)
