【LeetCode】嚼爛熱題100【持續更新】

2、字母異位詞分組

?方法一：排序+哈希表

思路：對每個字符串排序，排序后的字符串作為鍵插入到哈希表中，值為List<String>形式存儲單詞原型，鍵為排序后的字符串。

 Map<String, List<String>> m = new HashMap<>();

難點（重點）：

1、排序字符串

字符串本身不能直接排序，需要先利用str.toCharArray()轉換成為char[]，再利用Arrays.sort(s)；完成排序，但排序完的s就是char[]形式的。

2、哈希表map已有的接口computeIfAbsent(Key,Function)

map.computeIfAbsent(Key, Function)
  • ??若鍵存在??：直接返回對應的值（在本題中返回的就是對應的列表）。
  • ??若鍵不存在??：調用?Function?生成新值（本題中就是生成一個空的列表作為新的鍵對應的值），將鍵值對存入 Map，并返回新值。

這個方法的平替：但也需要知道map.getOrDefault（）方法

 List<String> list = map.getOrDefault(key, new ArrayList<String>());list.add(str);map.put(key, list);

值得注意的是：這個Key需要對應map的鍵值的類型。不能用char[]作為鍵的類型，因為所有數組類型（如?char[]）繼承自?Object，其?hashCode()?和?equals()?基于對象地址（而非內容）。

鍵可以選用基本類型和部分引用類型：

3、返回值要是List<List<String>>，

??Map.values()的返回值是類型為Collection<List<String>>的所有???值（List<String>）?? 的集合。要返回List<List<String>>只需要新建一個ArrayList<>（map.values()）即可。

class Solution {public List<List<String>> groupAnagrams(String[] strs) {Map<String, List<String>> m = new HashMap<>();for (String str : strs) {char[] s = str.toCharArray();Arrays.sort(s);// s 相同的字符串分到同一組m.computeIfAbsent(new String(s), k -> new ArrayList<>()).add(str);}return new ArrayList<>(m.values());}
}

3、?最長連續序列

給定一個未排序的整數數組?nums?，找出數字連續的最長序列（不要求序列元素在原數組中連續）的長度。

請你設計并實現時間復雜度為?O(n)?的算法解決此問題。

輸入：nums = [100,4,200,1,3,2]
輸出：4
解釋：最長數字連續序列是 [1, 2, 3, 4]。它的長度為 4。
class Solution {public int longestConsecutive(int[] nums) {Arrays.sort(nums);int ans = 1;int n = nums.length;if(n==0){return 0;}int tmp = nums[0];int count = 1;for(int i = 1;i<n;i++){if(nums[i]==tmp+1){count++;ans = Math.max(ans,count);tmp = nums[i];continue;}else if(nums[i]==tmp){continue;}else{count = 1 ;tmp = nums[i];ans = Math.max(ans,count);}}return ans;}
}

4、移動零

給定一個數組?nums，編寫一個函數將所有?0?移動到數組的末尾，同時保持非零元素的相對順序。

請注意?，必須在不復制數組的情況下原地對數組進行操作。

思路：

雙指針問題——>left指針指向待填充的位置，依次加1；right指針從小到大依次指向非零的。

相當于右指針每遇到一個非零的數，就把他按照left指針依次存到數組里

class Solution {public void moveZeroes(int[] nums) {int n = nums.length;if(n == 1 || n == 0){return;}int l = 0;int r = 0;while(r<n){if(nums[r] !=0 ){int tmp = nums[l];nums[l] = nums[r];nums[r] = tmp;r++;l++;}else{r++;}}}
}

5、盛最多水的容器

給定一個長度為?n?的整數數組?height?。有?n?條垂線，第?i?條線的兩個端點是?(i, 0)?和?(i, height[i])?。

找出其中的兩條線，使得它們與?x?軸共同構成的容器可以容納最多的水。

返回容器可以儲存的最大水量。

說明：你不能傾斜容器

示例 1：

輸入：[1,8,6,2,5,4,8,3,7]
輸出：49 
解釋：圖中垂直線代表輸入數組 [1,8,6,2,5,4,8,3,7]。在此情況下，容器能夠容納水（表示為藍色部分）的最大值為?49。

思路：

先框到最大，往里縮的時候，肯定是去變化那個最小的邊，因為是由于那個邊小面積才小的。

class Solution {public int maxArea(int[] height) {int l = 0;int r = height.length-1;int ans = 0;while(l<r){ans = Math.max(ans,(r-l)*Math.min(height[r],height[l]));if(height[l]<height[r]){l++;}else{r--;}}return ans;}
}

6、三數之和

給你一個整數數組?nums?，判斷是否存在三元組?[nums[i], nums[j], nums[k]]?滿足?i != j、i != k?且?j != k?，同時還滿足?nums[i] + nums[j] + nums[k] == 0?。請你返回所有和為?0?且不重復的三元組。

注意：答案中不可以包含重復的三元組。

思路：

如果是有序數組，遍歷第一個數，則三個數之和相當于在第一個數的右邊找兩個數和為-nums[i]。

值得注意的是，要避免重復，例如第一個數在遍歷的時候就要判斷是不是重復了；

后續如果滿足了，通過ans.add(List.of(三個數));即可，然后跳過重復的字段。

class Solution {public List<List<Integer>> threeSum(int[] nums) {Arrays.sort(nums);List<List<Integer>> ans = new ArrayList<>();int n = nums.length;for (int i = 0; i < n - 2; i++) {int x = nums[i];if (i > 0 && x == nums[i - 1]) continue; // 跳過重復數字if (x + nums[i + 1] + nums[i + 2] > 0) break; // 優化一if (x + nums[n - 2] + nums[n - 1] < 0) continue; // 優化二int j = i + 1;int k = n - 1;while (j < k) {int s = x + nums[j] + nums[k];if (s > 0) {k--;} else if (s < 0) {j++;} else { // 三數之和為 0ans.add(List.of(x, nums[j], nums[k]));//for (j++; j < k && nums[j] == nums[j - 1]; j++); // 跳過重復數字while(++j < k && nums[j] == nums[j - 1]);//for (k--; k > j && nums[k] == nums[k + 1]; k--); // 跳過重復數字while(--k>j && nums[k] == nums[k+1]);}}}return ans;}
}

7、接雨水

給定?n?個非負整數表示每個寬度為?1?的柱子的高度圖，計算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

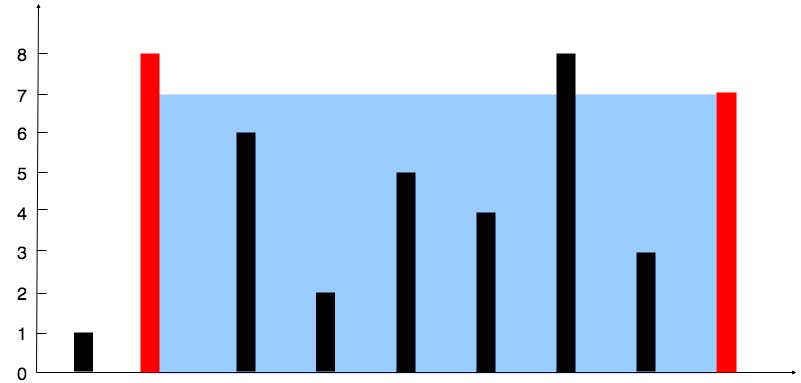
輸入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
輸出：6
解釋：上面是由數組 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度圖，在這種情況下，可以接 6 個單位的雨水（藍色部分表示雨水）。

思路：

接雨水經典問題：把每一個點當成一個桶，這個點能存多少水取決于他的左右兩側最高值的最小值，否則水會從兩邊流出去。如果左右兩邊的最值中相對小的數>這個桶本身的高度，則屬于正常接雨水，差值就是接到的雨水。

class Solution {public int trap(int[] height) {int n = height.length;int[] pre = new int[n];int[] lst = new int[n];pre[0] = height[0];lst[n-1] = height[n-1];for(int i = 1;i<n;i++){pre[i] = Math.max(pre[i-1],height[i]);}for(int i = n-2 ; i>=0 ;i--){lst[i] = Math.max(height[i],lst[i+1]);}int ans = 0;for(int i = 1;i < n-1 ; i++){int tmp = Math.min(pre[i],lst[i]);if(tmp > height[i]){ans+=(tmp-height[i]);}}return ans;}
}

8、無重復字符的最長子串

給定一個字符串?s?，請你找出其中不含有重復字符的?最長?子串?的長度。

示例?1:

輸入: s = "abcabcbb"
輸出: 3 
解釋: 因為無重復字符的最長子串是 "abc"，所以其長度為 3。

（1）官方得到滑動窗口（更快）

利用哈希表記錄每一個字母在滑動窗口中第一次出現的位置。

關鍵點的是怎么更新哈希表，通過左右指針，判斷右指針指向的字符是不是已經存在在哈希表中且在左指針的右邊，如果是，就相當于被滑動窗口框住了，也就是說框住的字符串由于右指針的加入，出現了重復的字符，所以要更新左指針和右指針指向的字符在滑動窗口中第一次出現的位置，把左指針指向右指針的字符原本第一次出現的位置+1的位置。

class Solution {public int lengthOfLongestSubstring(String s) {Map<Character, Integer> map = new HashMap<>();  // 記錄字符的最近一次出現位置int ans = 0;                                     // 最長子串長度int left = 0;                                    // 滑動窗口左邊界for (int right = 0; right < s.length(); right++) {char c = s.charAt(right);// 關鍵邏輯：如果字符 c 已經存在，且其位置 >= left，說明它在當前窗口內重復了if (map.containsKey(c) && map.get(c) >= left) {left = map.get(c) + 1;  // 將左邊界移動到重復字符的下一個位置}map.put(c, right);  // 更新字符 c 的最新位置ans = Math.max(ans, right - left + 1);  // 計算當前窗口長度，更新最大值}return ans;}
}

（2）我的思路

利用哈希表記錄每個字符出現的次數

需要一個公共參數index，判斷每次新加的字符是不是已經出現過，如果已經出現過，利用while循環執行把index++指向的字符出現的次數減1，直到新加的字符出現的次數不再大于1。

class Solution {public int lengthOfLongestSubstring(String S) {Map<Character,Integer> map = new HashMap<>();char[] s = S.toCharArray();int n = s.length;int ans = 0;int index = 0;for(int i = 0; i<n ; i++){if(map.containsKey(s[i])){map.put(s[i],map.get(s[i])+1);}else{map.put(s[i],1);}if(map.get(s[i])==1){ans = Math.max(ans,i-index+1);}while(map.get(s[i])>1){map.put(s[index],map.get(s[index])-1);index++;}}return ans;}
}

9、找到字符串中所有字母異位詞

給定兩個字符串?s?和?p，找到?s?中所有?p?的?異位詞?的子串，返回這些子串的起始索引。不考慮答案輸出的順序。

示例?1:

輸入: s = "cbaebabacd", p = "abc"
輸出: [0,6]
解釋:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的異位詞。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的異位詞。

(1)?

?標準的定長滑動窗口

關鍵：（1）利用 字符-‘a’ 把字符轉換為數字，設 int[ ] cnt = new int[26]

? ? ? ? ? ?（2）Arrays的一個接口方法：Arrays.equal（數組1，數組2）

? ? ? ? ? ?（3）滑動窗口三個步驟：入——>更新——>出

class Solution {public List<Integer> findAnagrams(String s, String p) {List<Integer> ans = new ArrayList<>();int[] cntP = new int[26]; // 統計 p 的每種字母的出現次數int[] cntS = new int[26]; // 統計 s 的長為 p.length() 的子串 s' 的每種字母的出現次數for (char c : p.toCharArray()) {cntP[c - 'a']++; // 統計 p 的字母}for (int right = 0; right < s.length(); right++) {cntS[s.charAt(right) - 'a']++; // 右端點字母進入窗口int left = right - p.length() + 1;if (left < 0) { // 窗口長度不足 p.length()continue;}if (Arrays.equals(cntS, cntP)) { // s' 和 p 的每種字母的出現次數都相同ans.add(left); // s' 左端點下標加入答案}cntS[s.charAt(left) - 'a']--; // 左端點字母離開窗口}return ans;}
}

(2)不定長窗口

class Solution {public List<Integer> findAnagrams(String s, String p) {List<Integer> ans = new ArrayList<>();int[] cnt = new int[26]; // 統計 p 的每種字母的出現次數for (char c : p.toCharArray()) {cnt[c - 'a']++;}int left = 0;for (int right = 0; right < s.length(); right++) {int c = s.charAt(right) - 'a';cnt[c]--; // 右端點字母進入窗口while (cnt[c] < 0) { // 字母 c 太多了cnt[s.charAt(left) - 'a']++; // 左端點字母離開窗口left++;}if (right - left + 1 == p.length()) { // s' 和 p 的每種字母的出現次數都相同ans.add(left); // s' 左端點下標加入答案}}return ans;}
}

10、?和為 K 的子數組

（1）枚舉

兩個for循環枚舉每一個數打頭的可能性。

public class Solution {public int subarraySum(int[] nums, int k) {int count = 0;for (int start = 0; start < nums.length; ++start) {int sum = 0;for (int end = start; end >= 0; --end) {sum += nums[end];if (sum == k) {count++;}}}return count;}
}

（2）前綴和優化

枚舉的思想是，確定1個開頭的數字nums[i]，然后依次求他后面所有數的和；

前綴和的思想：

定義 pre[i] 為 [0..i] 里所有數的和，則 pre[i] 可以由 pre[i?1] 遞推而來，即：

pre[i]=pre[i?1]+nums[i]。那么j到i的和就為pre[i]-pre[j-1]，判斷是否為k即可。

也就相當于找k+pre[j-1]是否存在

利用哈希表，把前綴和作為鍵，值為出現的次數。由于是按照從小到大順序走的，所以出現的次數只會是i之前的和，所以也就相當于遍歷了一遍0~i。?

public class Solution {public int subarraySum(int[] nums, int k) {int count = 0, pre = 0;HashMap < Integer, Integer > mp = new HashMap < > ();mp.put(0, 1);for (int i = 0; i < nums.length; i++) {pre += nums[i];if (mp.containsKey(pre - k)) {count += mp.get(pre - k);}mp.put(pre, mp.getOrDefault(pre, 0) + 1);}return count;}
}

要注意的是：這個key是子串和，值為個數。當pre = k時，?不管map里面有沒有和為0的，肯定是滿足的，所以提前存一個（0,1），??處理前綴和直接等于?k?的情況?。

11、?滑動窗口最大值

給你一個整數數組?nums，有一個大小為?k?的滑動窗口從數組的最左側移動到數組的最右側。你只可以看到在滑動窗口內的?k?個數字。滑動窗口每次只向右移動一位。

返回?滑動窗口中的最大值?。

示例 1：

輸入：nums = [1,3,-1,-3,5,3,6,7], k = 3
輸出：[3,3,5,5,6,7]
解釋：
滑動窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       31 [3  -1  -3] 5  3  6  7       31  3 [-1  -3  5] 3  6  7       51  3  -1 [-3  5  3] 6  7       51  3  -1  -3 [5  3  6] 7       61  3  -1  -3  5 [3  6  7]      7

方法一：單調隊列?

思路：

利用單調隊列求：

如果即將進入到框內的數更小，當大的走了這個小的有可能成為最大，但如果即將進來的數比末尾數大，那么這個末尾數就再也不會當做最大值，因為末尾值比即將進來的數小而且走的還早。也就相當于只在隊列中保存從大到小的數（單調隊列），出現小到大就扔掉小的；

當隊列中人數超了，扔掉隊首的數，下一個最大的只會是新隊首。

主要用到的ArrayDeque<>的方法：

（1）getLast()? ? ?getFirst();

（2）removeLast()

class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;int[] ans = new int[n - k + 1];Deque<Integer> q = new ArrayDeque<>(); // 雙端隊列for (int i = 0; i < n; i++) {// 1. 入while (!q.isEmpty() && nums[q.getLast()] <= nums[i]) {q.removeLast(); // 維護 q 的單調性}q.addLast(i); // 入隊// 2. 出if (i - q.getFirst() >= k) { // 隊首已經離開窗口了q.removeFirst();}// 3. 記錄答案if (i >= k - 1) {// 由于隊首到隊尾單調遞減，所以窗口最大值就是隊首ans[i - k + 1] = nums[q.getFirst()];}}return ans;}
}

?（簡單看了下，還沒理解）方法二 優先級隊列

我們不斷地移除堆頂的元素，直到其確實出現在滑動窗口中。此時，堆頂元素就是滑動窗口中的最大值。為了方便判斷堆頂元素與滑動窗口的位置關系，我們可以在優先隊列中存儲二元組?(num,index)，表示元素?num?在數組中的下標為?index。

算法步驟??

  1. ??初始化優先隊列??
    使用自定義比較器，隊列中的元素是包含數值和索引的數組。比較規則：

    • ??數值降序??：數值大的元素優先。
    • ??索引降序??：數值相同時，索引大的元素優先。
    PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<int[]>() {public int compare(int[] pair1, int[] pair2) {return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];}
});

  2. ??填充初始窗口??
    將前?k?個元素加入隊列：

    for (int i = 0; i < k; ++i) {pq.offer(new int[]{nums[i], i});
}

  3. ??處理第一個窗口的最大值??
    直接取隊首元素的值：

    ans[0] = pq.peek()[0];

  4. ??滑動窗口并更新結果??
    從第?k?個元素開始遍歷：

    • ??添加新元素到隊列??。
    • ??移除過期元素??：循環檢查隊首元素的索引是否在當前窗口的左側邊界之前（即?<= i - k），若過期則彈出。
    • ??記錄當前窗口的最大值??。
    for (int i = k; i < n; ++i) {pq.offer(new int[]{nums[i], i});while (pq.peek()[1] <= i - k) {pq.poll();}ans[i - k + 1] = pq.peek()[0];
}
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {public int compare(int[] pair1, int[] pair2) {return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];}});for (int i = 0; i < k; ++i) {pq.offer(new int[]{nums[i], i});}int[] ans = new int[n - k + 1];ans[0] = pq.peek()[0];for (int i = k; i < n; ++i) {pq.offer(new int[]{nums[i], i});while (pq.peek()[1] <= i - k) {pq.poll();}ans[i - k + 1] = pq.peek()[0];}return ans;}
}

12、最小覆蓋子串

給你一個字符串?s?、一個字符串?t?。返回?s?中涵蓋?t?所有字符的最小子串。如果?s?中不存在涵蓋?t?所有字符的子串，則返回空字符串?""?。

注意：

  • 對于?t?中重復字符，我們尋找的子字符串中該字符數量必須不少于?t?中該字符數量。
  • 如果?s?中存在這樣的子串，我們保證它是唯一的答案。

示例 1：

輸入：s = "ADOBECODEBANC", t = "ABC"
輸出："BANC"
解釋：最小覆蓋子串 "BANC" 包含來自字符串 t 的 'A'、'B' 和 'C'。

思路：

遍歷右指針，先加進來新的，加進來以后，只要cntS能夠覆蓋cntT，那么就一直更新返回值，并且更新左指針（左指針加一），直到不再覆蓋了。

所以引入了一個方法：能否覆蓋？

方法中，可以利用? for（int i = 'A' ; i <= 'Z' ; i++）來遍歷（再遍歷一遍‘a’到‘z’），只要cntT[i] >?cntS[i]，就代表S不覆蓋T，就返回false

class Solution {public String minWindow(String s, String T) {int[] cntS = new int[128];int[] cntT = new int[128];int n = s.length();int ansl = -1;int ansr = n;for(char t:T.toCharArray()){cntT[t] ++;}int l = 0;for(int r = 0 ;r<n;r++){cntS[s.charAt(r)]++;while(isCoverd(cntS,cntT)){if(r-l<ansr-ansl){ansl = l ;ansr = r ;}cntS[s.charAt(l)]--;l++;}}return ansl < 0 ? "" : s.substring(ansl,ansr+1);       }public boolean isCoverd(int[] cntS,int[] cntT){for(int i = 'A';i<='Z'; i++ ){if(cntS[i]<cntT[i]){return false;                         }}for(int i = 'a';i<='z'; i++ ){if(cntS[i]<cntT[i]){return false;                         }}return true;}
}

13、最大子數組和

給你一個整數數組?nums?，請你找出一個具有最大和的連續子數組（子數組最少包含一個元素），返回其最大和。

子數組是數組中的一個連續部分。

示例 1：

輸入：nums = [-2,1,-3,4,-1,2,1,-5,4]
輸出：6
解釋：連續子數組?[4,-1,2,1] 的和最大，為?6 。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/pingmian/77836.shtml
繁體地址，請注明出處：http://hk.pswp.cn/pingmian/77836.shtml
英文地址，請注明出處：http://en.pswp.cn/pingmian/77836.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

2025年最新版 Git和Github的綁定方法，以及通過Git提交文件至Github的具體流程(詳細版)

2025年最新版 Git和Github的綁定方法，以及通過Git提交文件至Github的具體流程(詳細版)

文章目錄 Git和Github的綁定方法與如何上傳至代碼倉庫一. 注冊 GitHub 賬號二.如何創建自己的代碼倉庫&#xff1a;1.登入Github賬號&#xff0c;完成登入后會進入如下界面&#xff1a;2.點擊下圖中紅色框選的按鈕中的下拉列表3.選擇New repostitory4.進入創建界面后&#xff0…
閱讀更多...
FPGA開發板這樣做？（一）-像 Arduino 一樣玩 FPGA

FPGA開發板這樣做？（一）-像 Arduino 一樣玩 FPGA

這也是一個系列文章&#xff0c;來源之前和粉絲們在評論區討論的國外對于FPGA的開發或者入門所做的努力。 基本一篇文章會介紹一個FPGA開發板&#xff0c;重點在于為開發板準備的開發方式&#xff08;和國內大不相同&#xff09;。 今天的主角-PulseRain M10&#xff1a;像 Ard…
閱讀更多...
【C++游戲引擎開發】第21篇：基于物理渲染（PBR）——統計學解構材質與光影

【C++游戲引擎開發】第21篇：基于物理渲染（PBR）——統計學解構材質與光影

引言 宏觀現象：人眼觀察到的材質表面特性（如金屬的高光銳利、石膏的漫反射柔和），本質上是微觀結構對光線的統計平均結果。 微觀真相：任何看似平整的表面在放大后都呈現崎嶇的微觀幾何。每個微表面（Microfacet）均為完美鏡面，但大量微表面以不同朝向分布時，宏觀上會表…
閱讀更多...
深入理解linux操作系統---第11講 bshell編程

深入理解linux操作系統---第11講 bshell編程

11.1 正則表達式 11.1.1 字符集 正則表達式的字符集包含三類核心要素&#xff1a; 普通字符&#xff1a;直接匹配單個字符&#xff0c;如a匹配字母a范圍字符集&#xff1a;[a-z]匹配所有小寫字母&#xff0c;[0-9A-F]匹配十六進制數字預定義字符集&#xff1a;\d等價于[0-9]…
閱讀更多...
C++中的引用：深入理解與實用示例

C++中的引用：深入理解與實用示例

文章目錄 C中的引用&#xff1a;深入理解與實用示例一、引用的基本概念二、引用作為別名的應用三、引用作為函數參數四、指針與引用的區別五、常量引用六、引用與返回值七、總結 C中的引用&#xff1a;深入理解與實用示例 在C編程中&#xff0c;“引用”是一個強大而重要的概念…
閱讀更多...
C#委托介紹

C#委托介紹

委托可以將方法作為參數傳遞&#xff0c;同時委托也可以自己作為參數傳遞 委托可分為自定義委托delegate 無返回值的Action 與有返回值的Func委托 也有匿名委托與Lamada 委托支持多播是事件的基礎 用處如在分線程調用主線程的UI invoke public delegate string Say(stri…
閱讀更多...
Node.js 模塊導入的基本流程

Node.js 模塊導入的基本流程

Node.js 模塊導入的基本流程&#xff0c;主要是 CommonJS 模塊加載機制&#xff08;即使用 require()&#xff09;的內部執行步驟。下面我用清晰的結構給你梳理一下這個過程&#xff1a; ? Node.js 模塊導入的基本流程&#xff08;使用 require()&#xff09; const someModu…
閱讀更多...
n8n 中文系列教程_02. 自動化平臺深度解析：核心優勢與場景適配指南

n8n 中文系列教程_02. 自動化平臺深度解析：核心優勢與場景適配指南

在低代碼與AI技術深度融合的今天&#xff0c;n8n作為開源自動化平臺正成為開發者提效的新利器。本文深度剖析其四大核心技術優勢——極簡部署、服務集成、AI工作流與混合開發模式&#xff0c;并基于真實場景測試數據&#xff0c;厘清其在C端高并發、多媒體處理等場景的邊界。 一…
閱讀更多...
【C++ Qt】信號和槽（內配思維導圖 圖文并茂 通俗易懂）

【C++ Qt】信號和槽（內配思維導圖 圖文并茂 通俗易懂）

每日激勵&#xff1a;“不設限和自我肯定的心態&#xff1a;I can do all things。 — Stephen Curry” 緒論?&#xff1a; 本章是Qt中的第三章&#xff0c;也是我們理解Qt中必備的點 信號槽&#xff0c;它本質由信號和槽兩個來實現&#xff0c;其中將細致的講述如何自定義信號…
閱讀更多...
【項目】基于MCP+Tabelstore架構實現知識庫答疑系統

【項目】基于MCP+Tabelstore架構實現知識庫答疑系統

基于MCPTabelstore架構實現知識庫答疑系統 整體流程設計&#xff08;一&#xff09;Agent 架構&#xff08;二&#xff09;知識庫存儲&#xff08;1&#xff09;向量數據庫Tablestore&#xff08;2&#xff09;MCP Server &#xff08;三&#xff09;知識庫構建&#xff08;1&a…
閱讀更多...
免費將靜態網站部署到服務器方法（僅支持HTML，CSS，JS）

免費將靜態網站部署到服務器方法（僅支持HTML，CSS，JS）

原視頻鏈接&#xff1a;把HTML免費部署到網站上&#xff0c;實現別人也能訪問的教程來啦QAQ_嗶哩嗶哩_bilibili 注意&#xff1a;僅支持HTML、CSS、JS。不支持Vue等框架。 1.打開網站www.wordpress.org 點擊紅框按鈕 點擊紅框按鈕下載wordpress模板文件并解壓。 將自己編寫的…
閱讀更多...
游戲引擎學習第235天:在 Windows 上初始化 OpenGL

游戲引擎學習第235天:在 Windows 上初始化 OpenGL

奇怪有問題 之前沒注意到 這個問題是Count 0 GlobalConstants_Renderer_UsedDebugCamer 打開的話會有Bug Count是零的話就不讓排序了 game.h: 查閱 TODO 列表 大家好&#xff0c;歡迎來到 game Hero&#xff0c;這是一檔我們在直播中一起編寫完整游戲的節目。不幸的是&a…
閱讀更多...
使用eCharts繪制中國地圖

使用eCharts繪制中國地圖

eCharts官網&#xff1a;https://echarts.apache.org/zh/index.html 1. 首先新建一個html頁面&#xff0c;并引入echarts <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-…
閱讀更多...
Linux與Anaconda環境部署與管理（運維交接）

Linux與Anaconda環境部署與管理（運維交接）

文章目錄 一、前言二、Linux基礎命令三、進程管理與監控四、后臺任務與服務管理五、Anaconda環境管理六、JAR包的運行與管理七、網絡與端口映射八、安全與權限管理九、故障排查與日志分析十、附錄 一、前言 本文將詳細介紹Linux系統下的常用命令以及Anaconda環境管理&#xff…
閱讀更多...
php：實現壓縮文件上傳、解壓、文件更名、刪除上傳臨時文件、存入數據庫等操作

php：實現壓縮文件上傳、解壓、文件更名、刪除上傳臨時文件、存入數據庫等操作

一、效果圖 1.上傳文件 2.壓縮包文件 3.itemno1文件 二層結構 或 三層結構 4.上傳到系統路徑\ItemNo 5.更名后的itemno1文件(命名：當天日期+六位隨機數) 二、普通實現 1、內容介紹 含有兩種結構 二層結構：zip->料號文件夾->料號文件三層結構：zip->總文件夾-&g…
閱讀更多...
基于大語言模型的減肥健身計劃系統設計與實現

基于大語言模型的減肥健身計劃系統設計與實現

基于大語言模型的減肥健身計劃系統設計與實現 【包含內容】 【一】項目提供完整源代碼及詳細注釋 【二】系統設計思路與實現說明 【三】功能演示與部署指南 【技術棧】 ①&#xff1a;系統環境&#xff1a;Python 3.x Django 4.2 ②&#xff1a;開發環境&#xff1a;Web服務…
閱讀更多...
c#開發大沖鋒游戲登錄器

c#開發大沖鋒游戲登錄器

1 前言 本文主要分享登錄器的簡要開發過程&#xff0c;只適合小白選手&#xff0c;高手請自動避讓。 此項目是復刻大沖鋒計劃中的子集。 &#xff08;注&#xff1a;大沖鋒是迅雷代理的一款次時代多職業第一人稱FPS射擊游戲&#xff0c;目前已經關服嗝屁。&#xff09; 2 …
閱讀更多...
Linux[基礎指令][2]

Linux[基礎指令][2]

Linux[基礎指令][2] cp(復制) 格式:cp [-rf] 源文件 {普通文件,目錄} 拷貝 cp -r 遞歸拷貝目錄 藍色為目錄,白色為具體文件 拷貝后面加一個不存在的文件會新建文件再拷貝 cp -ir -i是覆蓋的時候詢問 如果目標文件存在就會覆蓋原有文件 mv(重命名/剪切) 格式:mv 源文件…
閱讀更多...
React18+ 項目搭建-從初始化、技術選型到開發部署的全流程規劃

React18+ 項目搭建-從初始化、技術選型到開發部署的全流程規劃

搭建一個 React 項目需要從項目初始化、技術選型到開發部署的全流程規劃。以下是詳細步驟和推薦的技術棧&#xff1a; 一、項目初始化 1. 選擇腳手架工具 推薦工具&#xff1a; Vite&#xff08;現代輕量級工具&#xff0c;支持 React 模板&#xff0c;速度快&#xff09;&am…
閱讀更多...
人工智能學習框架完全指南（2025年更新版）

人工智能學習框架完全指南（2025年更新版）

一、核心框架分類與適用場景 人工智能框架根據功能可分為深度學習框架、機器學習框架、強化學習框架和傳統工具庫，以下是主流工具及選型建議： 1. 深度學習框架 （1）PyTorch 核心優勢：動態計算圖、靈活性強，適合科研與快速原型開發，支持多模態任務（如NLP、CV） 。技術生…
閱讀更多...
最新文章

Copyright @ 2022~2023