一、初識決策樹
????????想象一個生活中的場景,我們去水果店買一個西瓜,該怎么判斷一個西瓜是不是又甜又好的呢?我們可能會問自己一系列問題:
- 首先看看它的紋路清晰嗎?
- 如果“是”,那么它可能是個好瓜。
- 如果“否“,那我們可能會問下一個問題:敲起來聲音清脆嗎?
- 如果“是”,那么它可能還是個不錯的瓜。
- 如果“否“,那我們很可能就不會買它了。
????????這個過程,就是你大腦中的一棵“決策樹”。決策樹算法,就是讓計算機從數據中自動學習出這一系列問題和判斷規則的方法。
二、什么是決策樹
1. 核心思想
????????它的核心思想非常簡單:通過提出一系列問題,對數據進行層層篩選,最終得到一個結論(分類或預測)。每一個問題都是關于某個特征的判斷(例如:“紋路是否清晰?”),而每個答案都會引導我們走向下一個問題,直到得到最終答案。
2. 決策樹的結構
一棵成熟的決策樹包含以下部分:
- 根節點:代表第一個、也是最核心的問題(例如:“紋路清晰嗎?”)。它包含所有的初始數據。
- 內部節點:代表中間的問題(例如:“聲音清脆嗎?”)。
- 葉節點:代表最終的決策結果(例如:“買”或“不買”)。
- 分支:代表一個問題的可能答案(例如:“是”或“否”)。

三、決策樹的執行流程
1. 流程圖
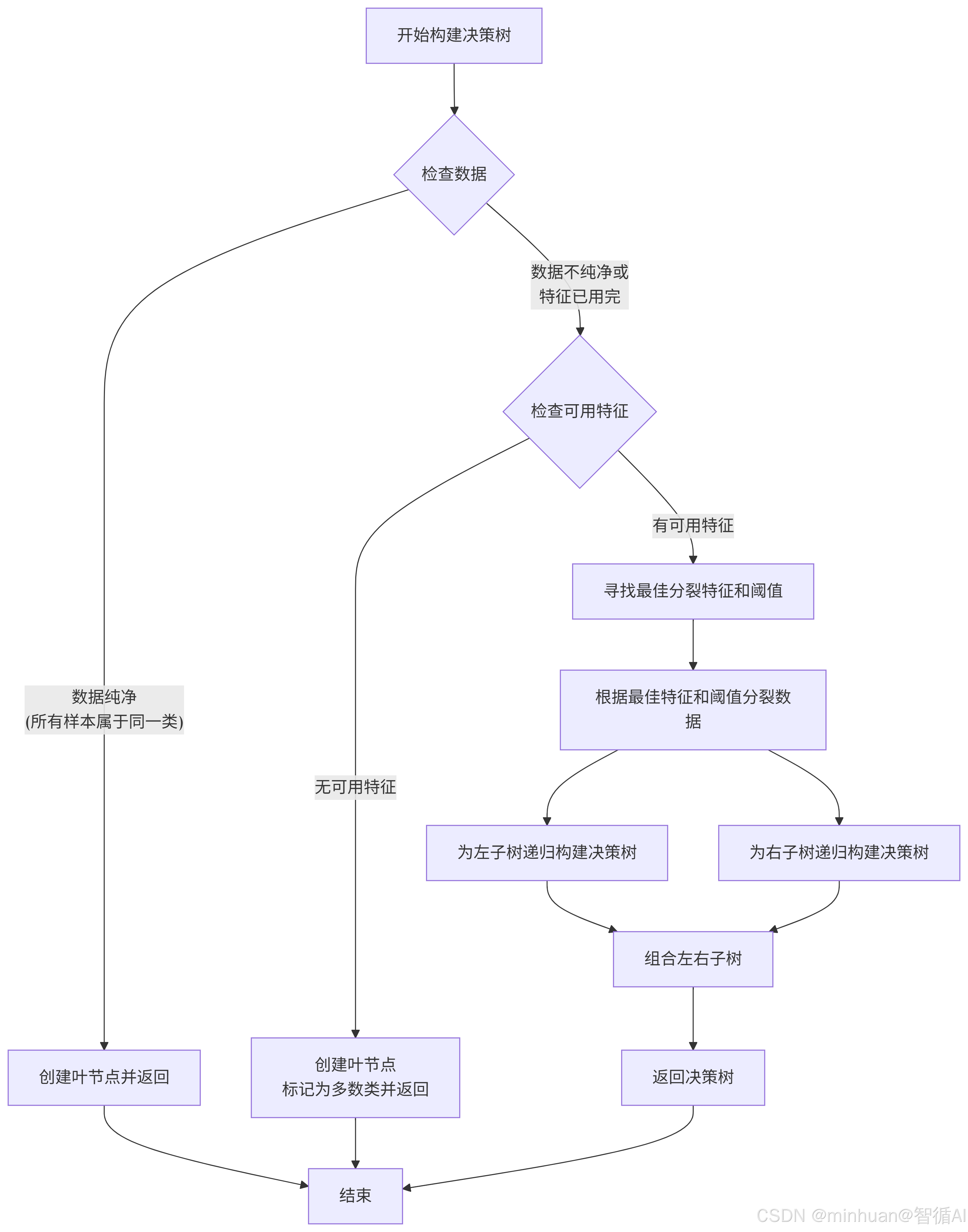
2. 構建過程
- 開始構建決策樹:算法從根節點開始,包含所有訓練樣本。
- 檢查數據:
- 如果當前節點的所有樣本屬于同一類別,則創建一個葉節點并返回
- 如果數據不純凈或還有特征可用,繼續下一步
- 檢查可用特征:
- 如果沒有更多特征可用于分裂,創建一個葉節點并標記為多數類
- 如果有可用特征,繼續下一步
- 尋找最佳分裂特征和閾值:
- 計算所有可能特征和閾值的信息增益/基尼不純度減少量
- 選擇能夠最大程度減少不純度的特征和閾值
- 根據最佳特征和閾值分裂數據:
- 將當前節點的數據分成兩個子集
- 左子集:特征值 ≤ 閾值的樣本
- 右子集:特征值 > 閾值的樣本
- 遞歸構建子樹:
- 對左子集遞歸調用決策樹構建算法
- 對右子集遞歸調用決策樹構建算法
- 組合子樹:將左右子樹組合到當前節點下
- 返回決策樹:返回構建完成的決策樹
三、怎么理解決策樹
現在我們來解決最關鍵的問題:計算機如何從一堆數據中自動找出最好的提問順序?
1. 關鍵問題:根據哪個特征進行分裂?
????????假設我們有一個西瓜數據集,包含很多西瓜的特征(紋路、根蒂、聲音、觸感...)和標簽(好瓜/壞瓜)。
在根節點,我們有所有數據。算法需要決定:第一個問題應該問什么? 是問“紋路清晰嗎?”還是“聲音清脆嗎?”?
????????選擇的標準是:哪個特征能最好地把數據分開,使得分裂后的子集盡可能純凈。所謂純凈,就是同一個子集里的西瓜盡可能都是好瓜,或者都是壞瓜。
2.?衡量標準:“不純度”的度量
我們如何量化“純度”呢?科學家們設計了幾種指標來衡量“不純度”:
- 信息熵:熵越高,表示數據越混亂,不純度越高。
- 基尼不純度: 計算一個隨機選中的樣本被錯誤分類的概率。基尼不純度越高,數據越不純。
3. 核心概念:信息增益
決策樹算法通過計算信息增益來決定用什么特征分裂。
信息增益 = 分裂前的不純度 - 分裂后的不純度
信息增益越大,說明這個特征分裂后,數據的純度提升得越多,這個特征就越應該被用來做分裂。
簡單比喻:
- 分裂前:一筐混在一起的紅豆和綠豆,此時純度不高。
- 用篩子A分裂:分成了兩堆,一堆大部分是紅豆,另一堆大部分是綠豆,此時純度顯著提升,信息增益大。
- 用篩子B分裂:分成了兩堆,但每一堆還是紅豆綠豆混合,此時純度沒什么變化,信息增益小。
- 顯然,篩子A是更好的選擇。在決策樹中,算法會嘗試所有篩子(特征),找到那個篩得最干凈的,即信息增益最大的。
4. 核心算法
- ID3: 使用信息增益作為分裂標準。缺點:傾向于選擇取值多的特征。
- C4.5: ID3的改進版,使用信息增益率作為標準,克服了ID3的缺點。
- CART: 最常用的算法,既可分類也可回歸。分類時使用基尼不純度,回歸時使用平方誤差。
5. 停止條件
不能無限地分下去,否則每個葉節點可能只有一個樣本(過擬合)。停止條件包括:
- 節點中的樣本全部屬于同一類別(已經100%純了)。
- 沒有更多的特征可供分裂。
- 樹達到了預設的最大深度。
- 節點中樣本數少于某個閾值(再分下去意義不大)。
四、構建決策樹
????????理論深奧讓人難以琢磨,我們來點實際的。用經典的scikit-learn庫,建一棵決策樹,細細的分析一下里面的每個步驟;
1. 示例代碼
import pandas as pd
import numpy as np
from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
from io import StringIO
import pydotplus
from IPython.display import Image# 1. 設置中文字體支持
# 嘗試使用系統中已有的中文字體
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans', 'Arial Unicode MS', 'Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False ?# 解決負號顯示問題# 2. 創建示例數據集(使用鳶尾花數據集,但用中文重命名)
iris = load_iris()
X = iris.data
y = iris.target# 創建中文特征名稱和類別名稱
chinese_feature_names = ['花萼長度', '花萼寬度', '花瓣長度', '花瓣寬度']
chinese_class_names = ['山鳶尾', '變色鳶尾', '維吉尼亞鳶尾']# 3. 劃分訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42
)# 4. 創建并訓練決策樹模型
clf = tree.DecisionTreeClassifier(criterion='gini', ? ? # 使用基尼不純度max_depth=3, ? ? ? ? ?# 限制樹深度,防止過擬合min_samples_split=2, ?# 節點最小分裂樣本數min_samples_leaf=1, ? # 葉節點最小樣本數random_state=42 ? ? ? # 隨機種子,確保結果可重現
)
clf.fit(X_train, y_train)# 5. 評估模型
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"模型準確率: {accuracy:.2%}")# 6. 可視化決策樹 - 方法1:使用Matplotlib(簡單但不支持中文特征名)
plt.figure(figsize=(20, 12))
tree.plot_tree(clf,feature_names=chinese_feature_names, ?# 使用中文特征名class_names=chinese_class_names, ? ? ?# 使用中文類別名filled=True, ? ? ? ? ? ? ? ? ? ? ? ? ?# 填充顏色表示類別rounded=True, ? ? ? ? ? ? ? ? ? ? ? ? # 圓角節點proportion=True, ? ? ? ? ? ? ? ? ? ? ?# 顯示比例而非樣本數precision=2 ? ? ? ? ? ? ? ? ? ? ? ? ? # 數值精度
)
plt.title("決策樹可視化 - 鳶尾花分類", fontsize=16)
plt.savefig('decision_tree_chinese.png', dpi=300, bbox_inches='tight')
plt.show()2. 結果展示
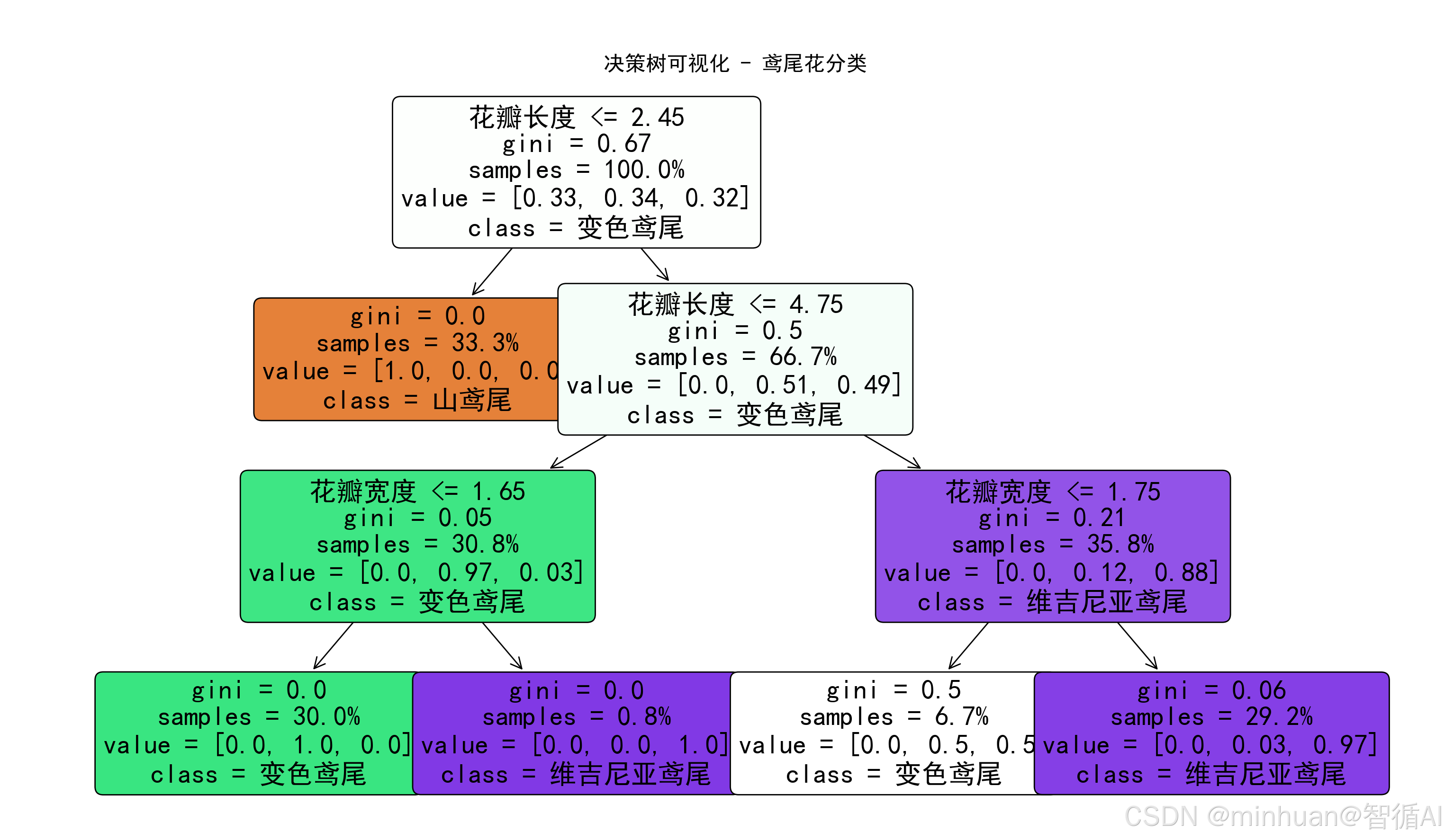
3. 決策的基礎:鳶尾花分類
????????這是一個鳶尾花分類的決策過程,首先簡單描述一下鳶尾花分類的基礎知識,鳶尾花分類是一個經典的機器學習入門問題,也是一個多類別分類任務。其目標是根據一朵鳶尾花的花瓣和花萼的測量數據,自動判斷它屬于三個品種中的哪一種。
接下來這些很重要,很重要,很重要!
3.1 三種鳶尾花
- Iris Setosa:山鳶尾,最容易識別,花瓣短而寬,花萼較大。
- Iris Versicolor:變色鳶尾,介于另外兩種之間,顏色多變。
- Iris Virginica:維吉尼亞鳶尾,最大最壯觀,花瓣和花萼尺寸都最大。
3.2 數據集的構成
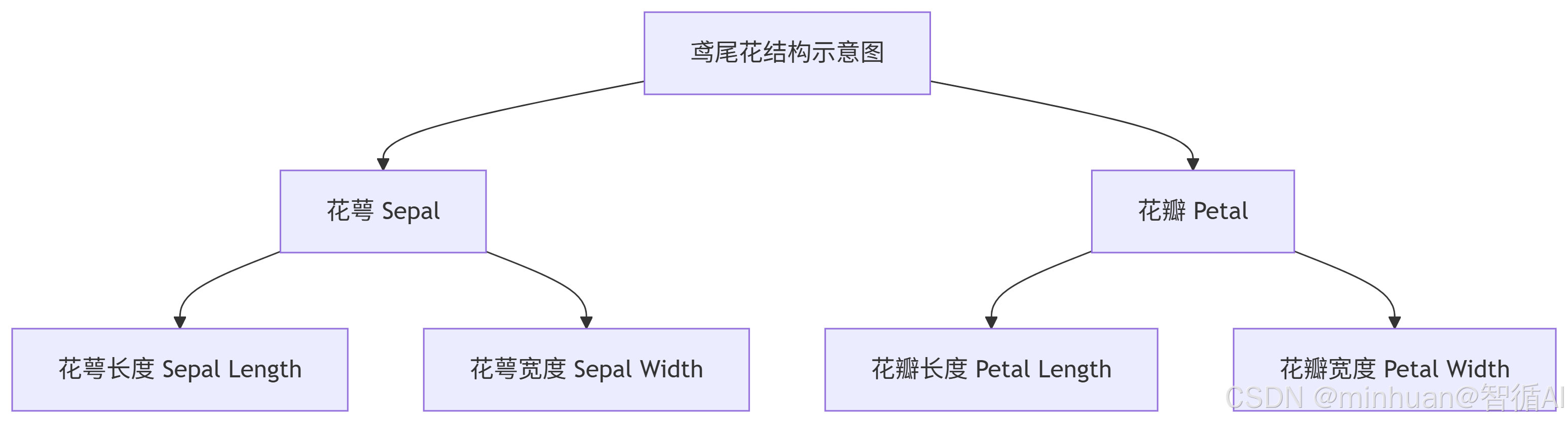
整個數據集就是一個大表格,有150行(代表150朵不同的花)和5列。
| 品種 (標簽) | 花萼長度 | 花萼寬度 | 花瓣長度 | 花瓣寬度 |
| Iris-setosa? | 5.1 | 3.5 | 1.4 | 0.2 |
| Iris-versicolor | 7.0 | 3.2 | 4.7 | 1.4 |
| Iris-virginica | 6.3 | 3.3 | 6.0 | 2.5 |
| ... | ... | ... | ... |
數據集包含150個樣本,每個樣本有4個特征和1個標簽:
- 4個特征(預測依據):
- ?sepal length (cm) - 花萼長度
- ?sepal width (cm) - 花萼寬度
- ?petal length (cm) - 花瓣長度
- ?petal width (cm) - 花瓣寬度
- 1個標簽(預測目標):
- ?species - 品種(0: Setosa, 1: Versicolor, 2: Virginica)
3.3 經典的鳶尾花數據集
它之所以成為經典,是因為它具備了一個完美教學數據集的所有特點:
- 簡單易懂:問題本身非常直觀,不需要專業知識。
- 維度適中:4個特征不多不少,易于可視化和理解,又能體現多維度分析的價值。
- 清晰可分離:Setosa與其他兩種花線性可分,Versicolor和Virginica之間存在重疊但仍有明顯模式,提供了一個從易到難的學習過程。
- 干凈完整:數據經過精心整理,沒有缺失值或異常值,讓學生可以專注于算法本身。
- 免費開源:被內置在幾乎所有機器學習庫中(如scikit-learn),易于獲取和使用。
4. 數據分析
????????看到這個圖,首先要明白這是在決策鳶尾花具體是屬于哪一種類型,每一層都有幾個值:花瓣長度、gini、samples、value、class,其中:
- gini:基尼不純度值,衡量隨機抽取兩個樣本,它們屬于不同類別的概率,越小表示節點純度越高,分類效果越好
- samples:當前節點包含的樣本數量
- value:樣本在三類鳶尾花中的分布
- class:當前節點的預測類別
先了解概念,在了解具體的公式和推導值;
4.1 第一步:判斷“花瓣長度 <= 2.45”
????????此處非常有意思,2.45是怎么來的,是固定的還是隨機抽取的,首先這不是隨意的,而是通過嚴密的數學計算和優化選擇得出的結果:
從最直觀理解,數據分布的角度,花瓣長度的數據分布一般在:
- Setosa的花瓣長度分布: ? ? ?1.0 - 2.0 cm
- Versicolor的花瓣長度分布: ?3.0 - 5.1 cm ?
- Virginica的花瓣長度分布: ? 4.5 - 6.9 cm
由上得知可以看到:
- Setosa的花瓣長度完全與其他兩種花不重疊
- 2.45cm正好落在Setosa的最大值(2.0cm)和Versicolor的最小值(3.0cm)之間
這個點能夠完美地將Setosa從其他兩種花中分離出來
其次,最有依據的是基于準確的數學方法,最佳分裂點(先了解,后面會細講):
- 在花瓣長度上,2.45cm附近的閾值能產生最低的gini值,即數據純度越高(先了解,后面會細講)
- 花瓣長度特征的整體區分效果最好
4.2 samples(樣本總量)100%
????????這個很好理解,此時抽取的是所有樣本,所有數量為100%。
4.3? value = [0.33, 0.34, 0.32]
????????value表示的是每個樣本在三類鳶尾花中的分布,這里也比較有趣味性了,按常理來說應該都是均分,都應該是0.3333,為什么會有差異呢,與訓練集和測試集的分布有關系,這個比例會隨著你劃分訓練集和測試集的方式不同而發生微小的變化。
簡單看看這個變化的過程:
4.3.1 數據的初始狀態:理論上應該是固定的
????????鳶尾花數據集本身有150個樣本,每個品種(Setosa, Versicolor, Virginica)各50個。因此,在整個數據集中,每個類別的比例是精確的:
????????value = [50/150, 50/150, 50/150] = [0.333..., 0.333..., 0.333...]
????????所以,如果你在根節點看到 value = [0.33, 0.34, 0.32] 而不是完美的 [0.333, 0.333, 0.333],這已經暗示了我們沒有使用全部150個樣本。
4.3.2 為什么我們看到的不是固定值?—— 訓練集與測試集的劃分
????????在機器學習中,我們不會用全部數據來訓練模型。為了評估模型的真實性能,我們通常會將數據劃分為訓練集和測試集。
- 訓練集:用于“教導”模型,讓它學習規律。
- 測試集:用于“考試”,評估模型在未見過的數據上的表現。
最常用的劃分比例是 80% 的數據用于訓練,20% 用于測試。
????????關鍵點就在這里:150 * 0.8 = 120。現在,訓練集只剩下120個樣本。原來每個類別有50個,但在隨機抽取80%后,每個類別在訓練集中的數量幾乎是 50 * 0.8 = 40,但不會那么精確。
- 可能Setosa被抽走了39個,Versicolor被抽走了41個,Virginica被抽走了40個。
- 那么在根節點,比例就變成了 [39/120, 41/120, 40/120] = [0.325, 0.341, 0.333]。
- 當這些值被四舍五入到小數點后兩位顯示時,就可能出現 [0.33, 0.34, 0.32] 或 [0.32, 0.34, 0.33] 等各種組合。
4.3.3 random_state 參數的作用
????????您可能注意到了上面代碼中的 random_state=42。這個參數控制了隨機抽樣的“種子”。
- 如果設置 random_state:每次運行代碼,劃分結果都是一樣的。因此 value 的值也是固定的。42 只是一個常用例子,你可以用任何數字。
- 如果不設置 random_state:每次運行代碼,都會進行一次新的隨機劃分。因此每次看到的 value 值都可能略有不同。
????????所以,value 的值是“固定”還是“變化”,完全取決于你的代碼配置。
4.3.4 抽取的流程
????????下面這張圖展示了數據如何從原始全集被隨機劃分到訓練集,從而導致節點中類別比例發生微小變化的過程:
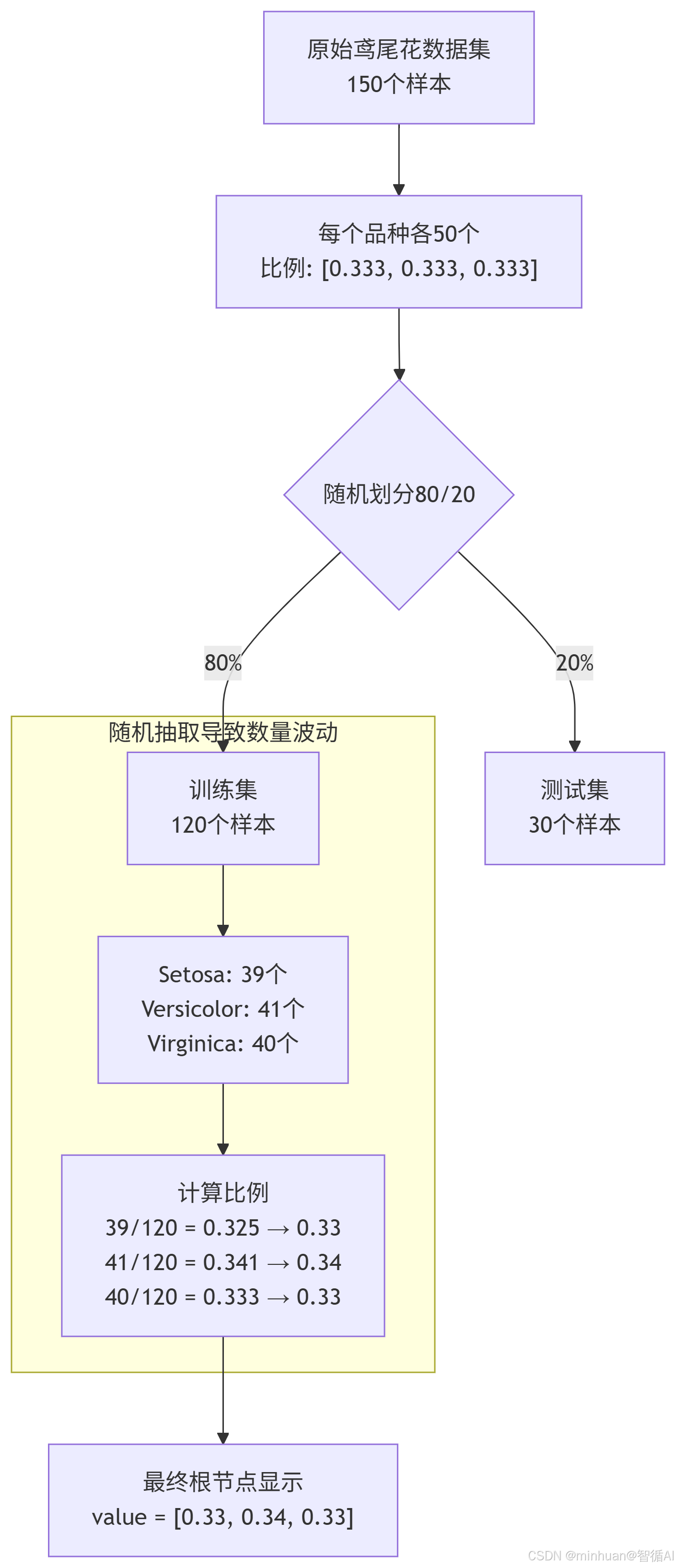
? ? ? ? 所以,看到的 [0.33, 0.34, 0.32] 是一個在隨機劃分訓練集后,各類別比例的正常、微小的波動表現,并不意味著數據或代碼有問題。
4.4?gini =? 0.67?
gini值計算的公式:
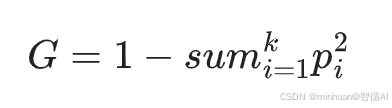
其中:
- ?k為類別總數(鳶尾花分類中 )
- ?Pi為第i類樣本占比
根節點參數:
- value = [0.33, 0.34, 0.32](三類鳶尾花樣本占比)
- G = 1 - (0.33的平方 + 0.43的平方 + 0.32的平方)= 1 - (0.1089+0.1156+0.1024) = 1 -? 0.3269 = 0.6731
- 結果四舍五入后與圖示根節點的0.67高度吻合
4.5 class = 變色鳶尾
????????對應的占比,中間的Iris Versicolor變色鳶尾比例為0.34居多,所以當前的預測類別偏重于變色鳶尾。
4.6 花瓣長度<=2.45的結果
4.6.1 結果成立
????????如果結果成立則走第二次的左側節點,直接判定為山鳶尾,流程結束。
強化值計算:
- value = [1,0, 0 ,0], 由于此節點一句明確是山鳶尾類型了,所有只有山鳶尾的樣本數,并為100%即1,其他則為0
- gini = 0.0 -> 計算方式:1 - (1.0*1.0+0*0+0*0) = 1-1 = 0
- samples =33.3% 從第一層的樣本比例繼承
- class =?山鳶尾,100%的山鳶尾類型選擇了
4.6.2 如果結果不成立
?????????如果結果成立則走第二次的右側節點,繼續下一步的決策,調整判斷參數,判斷“花瓣長度<=4.75”,觀察對應的參數值:
- samples = 66.7%,由于已經排除了不是山鳶尾類型,所以此時的樣本比例為1-33.3%=66.7%
- value = [0.0, 0.51, 0.49],同樣排除了山鳶尾類型,第一個樣本為0,第二個參考第一層的 0.34/(0.34 + 0.32) = 0.5151,第三個樣本參考 0.32/(0.34 + 0.32) = 0.4848
- gini = 0.5?-> 計算方式:1 - (0*0+0.51*0.51+0.49*0.49) = 1-0.5002?= 0.5
- class = 變色鳶尾,比例相對最高的類型
????????按照這樣的思路,逐步分析決策,最終匹配到最適合的類型;如果還是有疑問,可以從根節點開始,跟著它的條件一步步走,看看模型是如何根據花的尺寸來分類的。這就像看到了模型的“思考過程”,非常直觀!
五、決策樹的優缺點
1. 優點
- 極其直觀,易于解釋:這是它最大的優點!你可以把它展示給任何人,即使不懂技術也能理解。這在醫療、金融等領域非常重要。
- 需要很少的數據預處理:不需要對數據進行標準化或歸一化。
- 可以處理各種數據:既能處理數字(如花瓣長度),也能處理類別(如顏色紅/綠/藍)。
2. 缺點
- 容易過擬合:如果不加控制,樹會長得非常復雜,完美記憶訓練數據中的每一個細節(包括噪聲),但在新數據上表現很差。這就像死記硬背了考題答案,但不會舉一反三的學生。
六、 總結
決策樹是機器學習中最基礎、最直觀的算法之一:
- 通過計算信息增益(或基尼不純度減少),選擇最能區分數據的特征來提問。
- 使用scikit-learn庫幾行代碼就能實現,并且可以可視化,非常利于理解和解釋。
- 理解決策樹是學習機器學習非常好的一步,它不僅是一個強大的工具,其思想也是很多更復雜算法(如隨機森林、梯度提升樹)的基石。希望這篇基礎的講解能幫你幫你初步理解決策樹,在這個基礎上,后面我們講一下決策樹的基礎分裂點是怎么一步步計算出來的!



















