七、反向傳播算法

反向傳播Back Propagation 簡稱 BP 。 訓練神經網絡的核心算法之一，通過計算損失函數，相對于每個權重參數的梯度，來優化神經網絡的權重

1. 前向傳播

前向傳播是把數據經過各層神經元的運算并逐層向前傳輸，知道輸出層

1.1 數學表達

簡單的三層神經網絡（輸入，隱藏，輸出）前向傳播的基本步驟分析

1.1.1 輸入層到隱藏層

給定輸入x和權重w1 以及偏置b1，隱藏層的輸出

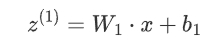
將z（1）通過激活函數激活

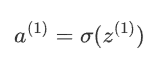
1.1.2 隱藏層到輸出層

隱藏層的輸出a（1）通過輸出層的權重矩陣w2和偏置b2生成最終的輸出：

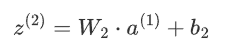
輸出層的激活函數a（2）最終預測結構

1.2 作用

輸出的結果用于預測或計算損失

反向傳播中，通過損失函數相對于每個參數的梯度來優化網絡

2.BP基礎梯度下降算法

梯度下降算法的目標是找到損失函數的最小參數，核心是沿著損失函數梯度的負方向更新參數，逐步逼近局部最優或全局最優，從而模型更好地訓練擬合訓練數據

2.1 數學描述

2.1.1 數學公式

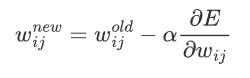
α是學習率

學習率太小：增加訓練的時間和算力成本

學習率太大，大概率跳過最優解，進入無線的訓練和震蕩

所以學習率要隨著訓練的變化而進行

2.1.2 過程闡述

初始化參數 Θ，權重w和偏置b

計算梯度：損失函數 L(θ)對參數θ的梯度，表示損失函數在參數空間的變化率。

更新參數：按照梯度下降公式更新參數：，其中，\alpha 是學習率，用于控制更新步長。

迭代更新：重復【計算梯度和更新參數】步驟，直到某個終止條件（如梯度接近0、不再收斂、完成迭代次數等）。

2.2 傳統下降方式

2.2.1 批量梯度下降BGD

BGD

特點：每次更新參數前，使用整個訓練集來計算梯度

優點：收斂穩定，更準確地沿著損失函數的真實梯度方向下降

缺點：數據集大的時候 計算量很大，更新慢；需要大內存

公式：

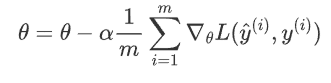
其中，m 是訓練集樣本總數，是第 i 個樣本及其標簽是第 i 個樣本預測值。

例如，在訓練集中有100個樣本，迭代50輪。

那么在每一輪迭代中，都會一起使用這100個樣本，計算整個訓練集的梯度，并對模型更新。

所以總共會更新50次梯度。

import torch
from torch.utils.data import TensorDataset, DataLoader
from torch import nn, optim# 生成隨機輸入數據和標簽
x = torch.rand(1000, 10)  # 1000 個樣本，每個樣本 10 個特征
y = torch.rand(1000, 1)   # 1000 個樣本對應的標簽# 將數據封裝為 TensorDataset 格式
dataset = TensorDataset(x, y)# 創建 DataLoader，用于批量加載數據
dataloader = DataLoader(dataset, batch_size=len(dataset))  # 這里設置 batch_size 為整個數據集大小，相當于一次性加載全部數據# 定義線性回歸模型，輸入特征維度為 10，輸出維度為 1
model = nn.Linear(10, 1)# 定義均方誤差損失函數
criterion = nn.MSELoss()# 定義隨機梯度下降優化器，學習率為 0.01
optimizer = optim.SGD(model.parameters(), lr=0.01)# 設置訓練輪數為 100
epochs = 100# 開始訓練循環
for epoch in range(epochs):# 遍歷數據加載器中的每個批次數據for b_x, b_y in dataloader:# 清空梯度，避免梯度累積optimizer.zero_grad()# 前向傳播，獲取模型輸出output = model(b_x)# 計算損失loss = criterion(output, b_y)# 反向傳播，計算梯度loss.backward()# 更新模型參數optimizer.step()# 打印當前輪數和損失值print("Epoch %d, Loss: %f" % (epoch, loss.item()))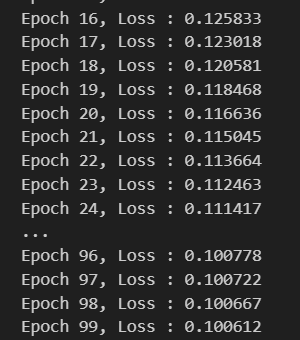

2.2.2 隨機梯度下降SGD

SGD

特點：每次更新參數時，僅使用一個樣本來計算梯度

優點：更新頻率高 計算快 適合大規模數據

能跳出局部最小值 有助于找到全局最優解

公式： 收斂不穩定，容易震蕩 因為樣本的梯度可能不完全代表整體方向

需要較小的學習率來緩解震蕩

公式

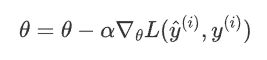
其中，是當前隨機抽取的樣本及其標簽。

如果訓練集有100個樣本，迭代50輪，那么每一輪迭代，會遍歷這100個樣本，每次會計算某一個樣本的梯度，然后更新模型參數。

換句話說，100個樣本，迭代50輪，那么就會更新100*50=5000次梯度。

因為每次只用一個樣本訓練，所以迭代速度會非常快。

但更新的方向會不穩定，這也導致隨機梯度下降，可能永遠都不會收斂。

不過也因為這種震蕩屬性，使得隨機梯度下降，可以跳出局部最優解。

這在某些情況下，是非常有用的。

x = torch.rand(1000,10)
y = torch.rand(1000,1)dataset = TensorDataset(x,y)
dataloader = DataLoader(dataset,batch_size =1)model = nn.Linear(10,1)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(),lr = 0.01)epochs = 100for epoch in range(epochs):for b_x,b_y in dataloader:optimizer.zero_grad()output = model(b_x)loss = criterion(output,b_y)loss.backward()optimizer.step()print("Epoches %d , Loss: %f" %(epoch,loss.item()))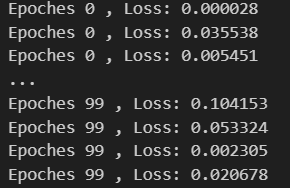

2.2.3 小批量梯度下降MGBD

MGBD

特點 ：每次更新參數 使用一小部分的訓練集?

優點： 在效率和收斂穩定性之間取平衡

能利用向量化加速計算，如GPU

缺點 ： 選擇適當的批量比較困難，通常根據硬件的算力32/64/128/256等

公式

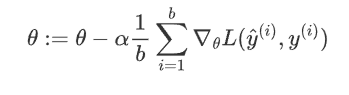
• 其中，b 是小批量的樣本數量，也就是 batc_size。

例如，如果訓練集中有100個樣本，迭代50輪。

如果設置小批量的數量是20，那么在每一輪迭代中，會有5次小批量迭代。

換句話說，就是將100個樣本分成5個小批量，每個小批量20個數據，每次迭代用一個小批量。

因此，按照這樣的方式，會對梯度，進行50輪*5個小批量=250次更新。

x = torch.randn(1000,10)
y = torch.randn(1000,1)dataset = TensorDataset(x,y)dataloader = DataLoader(dataset, batch_size=100, shuffle=True)model = nn.Linear(10,1)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)epochs = 100for epoch in range(epochs):for b_x,b_y in dataloader:optimizer.zero_grad()output = model(b_x)loss = criterion(output,b_y)loss.backward()optimizer.step()print("Epoch %d , Loss : %f" %(epoch+1,loss.item()))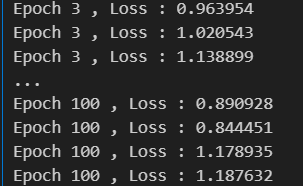

?

2.3 存在的問題

收斂速度慢：BGD和MBGD使用固定學習率，太大會導致震蕩，太小又收斂緩慢。

局部最小值和鞍點問題：SGD在遇到局部最小值或鞍點時容易停滯，導致模型難以達到全局最優。

訓練不穩定：SGD中的噪聲容易導致訓練過程中不穩定，使得訓練陷入震蕩或不收斂。

2.4 優化下降方式

用來提高收斂速度或穩定性

2.4.1 指數加權平均

? ? ? ? EMA。是一種平滑時間序列。對過去賦值予不同的權重計算平均值。與簡單移動平均不同，EMA賦值最近的數據給更高的權重，較遠的數據權重較低，這樣更敏感反映變化趨勢。

????????

比如今天股市的走勢，和昨天發生的國際事件關系很大，和6個月前發生的事件關系相對肯定小一些。

給定時間序列\{x_t\}，EMA在每個時刻 t 的值可以通過以下遞推公式計算：

當t=1時：

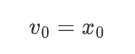
當t>1時：

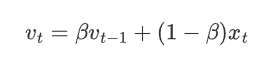
其中：

• v_t 是第 t 時刻的EMA值；

• x_t 是第 t 時刻的觀測值；

• \beta 是平滑系數，取值范圍為 0\leq \beta < 1。\beta 越接近 1，表示對歷史數據依賴性越高；越接近 0 則越依賴當前數據。

公式推導：

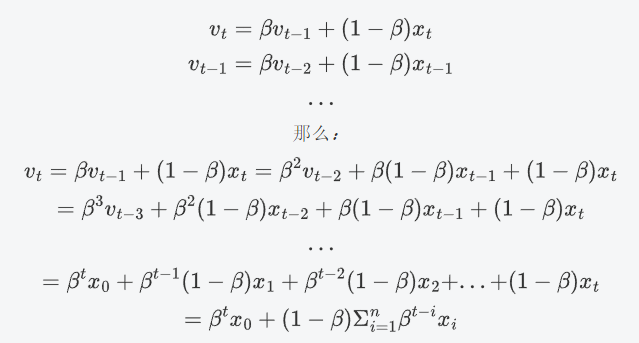
從上述公式可知：

• 當 β接近 1 時，β^k衰減較慢，因此歷史數據的權重較高。

• 當 β接近 0 時，β^k衰減較快，因此歷史數據的權重較低。

示例?

假設我們有一組數據 x=[1,2,3,4,5]，我們選擇 β=0.1和β=0.9 來計算 EMA。

（1）β=0.1

1. 初始化：

   EMA_0=x_0=1

2. 計算后續值：

   

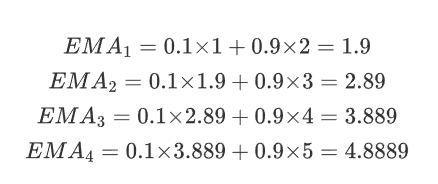
最終，EMA 的值為 [1,1.9,2.89,3.889,4.8889]。

（2）β=0.9

1. 初始化：

   EMA_0=x_0=1

2. 計算后續值：

   

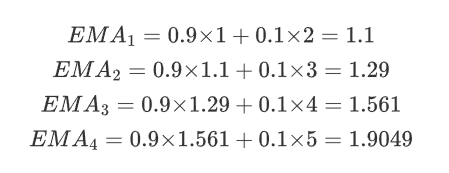
最終，EMA 的值為 [1,1.1,1.29,1.561,1.9049]。

可以看到：

• 當 β=0.9 時，歷史數據的權重較高，平滑效果較強。EMA值變化緩慢（新數據僅占10%權重），滯后明顯。

• 當 β=0.1時，近期數據的權重較高，平滑效果較弱。EMA值快速逼近最新數據（每次新數據占90%權重）。

2.4.2 Momentunm

動量是梯度下降的優化方法，更好應對梯度變化和梯度消失問題，提高模型的效率和穩定性，它通過引入指數加權平均來積累歷史梯度信息，形成“動量Momentum”，幫助算法更快越過局部最優或鞍點。

兩步：

1.計算動量項 ：

v（t-1）是之前的動量項；

β是動量系數（通常0.9

是當前的梯度

2.更新參數

用動量項更新參數

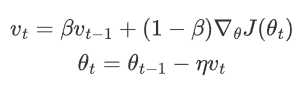
特點

? ? ? ? 慣性效應 ：會加入之前梯度的累計，像是有慣性，不會因為遇到鞍點導致梯度逼近而停滯

? ? ? ? 減少震蕩 ： 平滑了梯度更新，減少在鞍點附近的震蕩，幫助優化過程的穩步推進

? ? ? ? 加速收斂 ： 持續在某個方向推進，能夠快速穿過鞍點區域，避免在鞍點附近的長時間停留

在方向上的作用：

?（1）梯度方向一致時

如果多個梯度在多個連續時刻方向一致（指向同一個方向）Monmentum會積累，更新速度加快

（2）梯度不一致時

梯度方向在不同時刻不一致(震蕩） Monementum會通過積累歷史的梯度信息部分抵消這些震蕩

（3）局部最優或鞍點附近

在局部最優或者鞍點附近，梯度會變很小，導致標準梯度下降法停滯，Monmentum通過歷史積累，可以幫忙更新參數越過這些區域

動量方向與梯度方向一致

（1）梯度方向一致時

? ? ? ? 多個時刻方向一致，動量會逐漸累計，動量方向與梯度方向一致。

（2）幾何意義

? ? ? ? 如果損失函數形狀時平滑單調的，Momentum會加速參數的更新，幫忙快速收斂

動量方向與梯度方向不一致時

? （1）梯度方向不一致

梯度來回震蕩，動量vt會平滑這些變化，使更新路徑更加穩定

（2） 幾何意義

如果損失函數使復雜切非凸的，Momentum會通過累計的梯度信息抵消部分震蕩，讓路徑更加平滑

總結：

動量項更新：利用當前梯度和歷史動量來計算新的動量項。

權重參數更新：利用更新后的動量項來調整權重參數。

梯度計算：在每個時間步計算當前的梯度，用于更新動量項和權重參數。

Monmentum算法使梯度值的平滑調整，并沒有對梯度下降的學習率進行優化

import torch.nn as nn
import torch
model = nn.Linear(10, 1)
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01,momentum=0.9)x = torch.randn(100, 10)
y = torch.randn(100, 1)for epoch in range(100):optimizer.zero_grad()outputs = model(x)loss = criterion(outputs, y)loss.backward()optimizer.step()print(F"Epoch {epoch+1}，Loss : {loss.item():.4f}")

?2.4.5 AdaGrad

? ? ? ? 為每個參數引入獨立的學習率，根據歷史梯度的平方和來調整學習率，所以頻繁更新參數，學習率會逐漸減小，反之亦反。AdaGrad避免了統一學習率的不足，更多用于處理稀疏數據和梯度變化大的問題

AdaGrad流程：

1.初始化：

? ? ? ? 設置參數θ0和學習率η。

? ? ? ? 梯度累計平方的向量G0初始化為零向量

2.梯度計算

? ? ? ? 在每個時間步t，計算損失函數J(θ)對參數θ的梯度

3. 累計梯度的平方

? ? ? ? 每個參數i累計梯度的平方：

???????

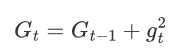
Gt使累計的梯度平方和，gt使第i個參數在時間步t的梯v

?

4.參數更新

利用累計的梯度平方來更新參數

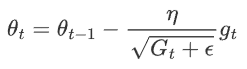
?η使全局的初始學習率

ε使一個非常小的常數，用于避免除零操作通常10的－8

是自適應調整后的學習率

AdaGrad為每個參數分配不同的學習率

? ? ? ? 對于梯度較大的參數，Gt較大，學習率較小，從而避免更新過快

? ? ? ? 反之亦反

可以將AdaGrad類比為

? ? ? ? 梯度較大的參數，類似陡峭的山坡，需要較小的步長，避免跨度過大

? ? ? ? 梯度小，平緩的山坡，較大的步長來加速收斂

優點：

• 自適應學習率：由于每個參數的學習率是基于其梯度的累積平方和 G_{t,i} 來動態調整的，這意味著學習率會隨著時間步的增加而減少，對梯度較大且變化頻繁的方向非常有用，防止了梯度過大導致的震蕩。

• 適合稀疏數據：AdaGrad 在處理稀疏數據時表現很好，因為它能夠自適應地為那些較少更新的參數保持較大的學習率。

缺點：

1. 學習率過度衰減：隨著時間的推移，累積的時間步梯度平方值越來越大，導致學習率逐漸接近零，模型會停止學習。

2. 不適合非稀疏數據：在非稀疏數據的情況下，學習率過快衰減可能導致優化過程早期停滯。

model = torch.nn.Linear(10,1)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.Adagrad(model.parameters(), lr=0.01)x = torch.randn(100,10)
y = torch.randn(100,1)for epoch in range(1000):optimizer.zero_grad()outputs = model(x)loss = criterion(outputs, y)loss.backward()optimizer.step()print(F"Epoch:{epoch+1},Loss:{loss.item():.4f}")

2.4.4 RMSProp

不是簡單地累積所以梯度平方和。而是使用指數加權平均來逐步平均來逐步衰減時候的梯度信息。它引入指數加權平均來累積歷史梯度的平方，動態調整學習率

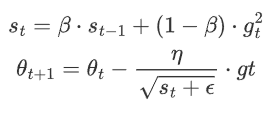
是當前時刻的指數加權平均梯度平方

β是衰減因子，通常0.9

η是初始學習率

?是一個小常數通常（10的－8）防止除0

gt是當前時刻梯度

優點

• 適應性強：RMSProp自適應調整每個參數的學習率，對于梯度變化較大的情況非常有效，使得優化過程更加平穩。

• 適合非稀疏數據：相比于AdaGrad，RMSProp更加適合處理非稀疏數據，因為它不會讓學習率減小到幾乎為零。

• 解決過度衰減問題：通過引入指數加權平均，RMSProp避免了AdaGrad中學習率過快衰減的問題，保持了學習率的穩定性

缺點

依賴于超參數的選擇：RMSProp的效果對衰減率γ和學習率 η的選擇比較敏感，需要一些調參工作。

model = nn.Linear(10, 1)
criterion = nn.MSELoss()
optimizer = torch.optim.RMSprop(model.parameters(), lr=0.01,alpha=0.9,eps = 1e-8)x = torch.randn(100,10)
y = torch.randn(100,1)for epoch in range(100):optimizer.zero_grad()outputs = model(x)loss = criterion(outputs, y)loss.backward()optimizer.step()print(F"Epoch : {epoch+1},Loss:{loss.item():.4f}")

2.4.5 Adam

將動量和RMSProp的優點結合

• 動量法：通過一階動量（即梯度的指數加權平均）來加速收斂，尤其是在有噪聲或梯度稀疏的情況下。

• RMSProp：通過二階動量（即梯度平方的指數加權平均）來調整學習率，使得每個參數的學習率適應其梯度的變化。

Adam過程

? ? ? ? 初始化：

? ? ? ? 初始化參數θ0和學習率η

? ? ? ? 初始化一階動量估計m0 = 0 和二階動量估計v0 =0

? ? ? ? 設定動量項的衰減率β和二階動量的衰減率β2，通常β1 = 0.9 ； β2 = 0.999

? ? ? ? 設定一個小常數ε（10的-8次方）防止除零的錯誤

2 梯度計算

? ? ? ? ?在每個時間步t，計算損失函數J（θ）對參數θ的梯度gt =?

3 一階動量估計（梯度的指數加權平均）

? ? ? ? 更新一階動量估計

????????

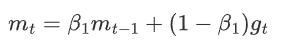
其中mt是當前時間步t的一階動量估計，表示梯度單獨指數加權平均

4 二階動量估計（梯度平方的指數加權平均）

? ? ? ? 更新二階動量估計

????????

vt是當前時間步t的二階動量估計，表示梯度平方的指數加權平均

5 偏差校正

由于一階動量和二階動量在初始階段可能會有偏差，以二階動量為例：

在計算指數加權平均時，初始化 v_{0}=0，那么，得到，顯然得到的 v_{1} 會小很多，導致估計的不準確，以此類推：

根據：，把 v_{1} 帶入后， 得到：，導致 v_{2} 遠小于 g_{1} 和 g_{2}，所以 v_{2} 并不能很好的估計出前兩次訓練的梯度。

所以這個估計是有偏差的。

使用以下公式進行偏差校正：

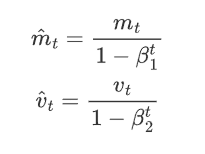
6 參數更新

使用校正后的動量估計更新參數

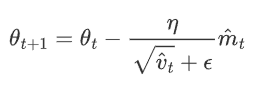
優點

1. 高效穩健：Adam結合了動量法和RMSProp的優勢，在處理非靜態、稀疏梯度和噪聲數據時表現出色，能夠快速穩定地收斂。

2. 自適應學習率：Adam通過一階和二階動量的估計，自適應調整每個參數的學習率，避免了全局學習率設定不合適的問題。

3. 適用大多數問題：Adam幾乎可以在不調整超參數的情況下應用于各種深度學習模型，表現良好。

缺點

1. 超參數敏感：盡管Adam通常能很好地工作，但它對初始超參數（如 β1、β2）仍然較為敏感，有時需要仔細調參。

2. 過擬合風險：由于Adam會在初始階段快速收斂，可能導致模型陷入局部最優甚至過擬合。因此，有時會結合其他優化算法（如SGD）使用。

2.5 總結

? ? ? ? 梯度下降算法通過不斷更新參數來最小化損失函數模式反向傳播算法中計算權重調整的基礎，根據數據規模和計算資源，選擇合適的梯度下降方法可以顯著提高模型訓練效果

????????Adam是目前最為流行的優化算法之一，因其穩定性和高效性，廣泛應用于各種深度學習模型的訓練中。

model = nn.Linear(10, 1)
criterion = nn.MSELoss()optimizer = torch.optim.Adam(model.parameters(), lr=0.01,betas=(0.9, 0.999),eps = 1e-08)x = torch.randn(100, 10)
y = torch.randn(100, 1)for epoch in range(100):optimizer.zero_grad()outputs = model(x)loss = criterion(outputs, y)loss.backward()optimizer.step()print(F"Epoch : {epoch+1},Loss : {loss.item():.4f}")