堆排序（Heap Sort）是一種基于二叉堆數據結構的高效排序算法，由計算機科學家 J. W. J. Williams 于 1964 年提出。它結合了選擇排序的思想和二叉堆的特性，具有時間復雜度穩定（O (nlogn)）、原地排序（空間復雜度 O (1)） 等優點，在大規模數據排序場景中應用廣泛。

堆的基本概念與性質 🎂

二叉堆的定義?

二叉堆是一種完全二叉樹（除最后一層外，每層節點均滿，最后一層節點靠左排列），分為兩種類型：?

最大堆：每個父節點的值大于等于其左右子節點的值（parent.val ≥ left.val 且 parent.val ≥ right.val）。?
最小堆：每個父節點的值小于等于其左右子節點的值（parent.val ≤ left.val 且 parent.val ≤ right.val）。? 堆排序中通常使用最大堆，本文以最大堆為例講解。

?

堆的存儲結構 🎂

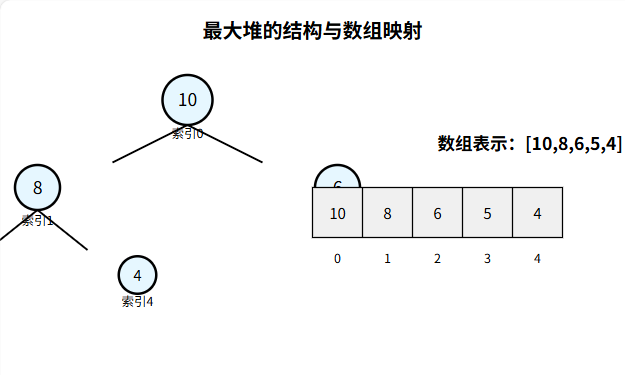
堆通常用數組實現，利用完全二叉樹的性質映射節點索引（假設數組索引從 0 開始）：?

對于節點 i：?
左子節點索引：2i + 1
?右子節點索引：2i + 2?
父節點索引：(i - 1) / 2（整數除法）

構建最大堆?

構建最大堆需從最后一個非葉子節點開始，依次向前執行堆調整操作。最后一個非葉子節點的索引為 (n / 2) - 1（n 為數組長度）。

構建過程代碼：

private void buildMaxHeap(int[] arr) {int n = arr.length;// 從最后一個非葉子節點開始調整for (int i = (n / 2) - 1; i >= 0; i--) {maxHeapify(arr, n, i);}
}

堆排序完整實現? 🎂

算法流程?

調用 buildMaxHeap 將數組轉為最大堆。?
初始化堆大小 heapSize = n。?
循環 n - 1 次：?
交換堆頂（arr[0]）與堆尾（arr[heapSize - 1]）元素。?
減小堆大小（heapSize–）。?
調用 maxHeapify 調整堆頂元素，維護剩余元素的堆性質。

堆排序圖示

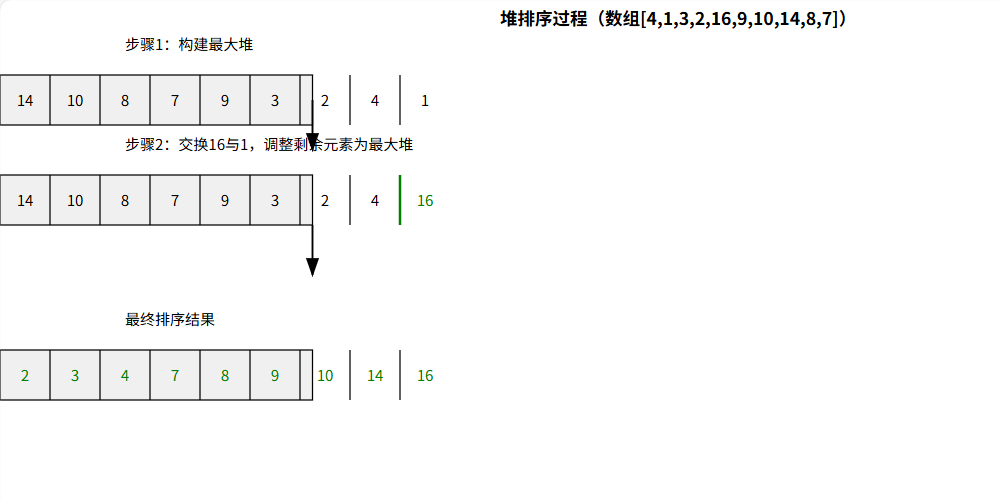
程序代碼：

public class HeapSort {public void sort(int[] arr) {int n = arr.length;if (n <= 1) return;// 步驟1：構建最大堆buildMaxHeap(arr);// 步驟2：排序階段int heapSize = n;for (int i = n - 1; i > 0; i--) {// 交換堆頂與當前堆尾swap(arr, 0, i);heapSize--; // 堆大小減1// 調整剩余元素為最大堆maxHeapify(arr, heapSize, 0);}}private void buildMaxHeap(int[] arr) {int n = arr.length;for (int i = (n / 2) - 1; i >= 0; i--) {maxHeapify(arr, n, i);}}private void maxHeapify(int[] arr, int heapSize, int i) {int left = 2 * i + 1;int right = 2 * i + 2;int maxIndex = i;if (left < heapSize && arr[left] > arr[maxIndex]) {maxIndex = left;}if (right < heapSize && arr[right] > arr[maxIndex]) {maxIndex = right;}if (maxIndex != i) {swap(arr, i, maxIndex);maxHeapify(arr, heapSize, maxIndex);}}private void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}public static void main(String[] args) {int[] arr = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7};HeapSort heapSort = new HeapSort();heapSort.sort(arr);System.out.println(Arrays.toString(arr)); // 輸出：[1, 2, 3, 4, 7, 8, 9, 10, 14, 16]}
}

復雜度分析?

時間復雜度：?
構建最大堆：O (n)（嚴格證明需用到堆的高度求和，結果為 O (n)）。?
排序階段：共執行 n-1 次堆調整，每次調整為 O (logn)，總時間 O (nlogn)。?
整體時間復雜度：O (nlogn)，且最壞情況下仍為 O (nlogn)，穩定性優于快速排序。?
空間復雜度：O (1)，原地排序，僅需常數級額外空間。

LeetCode 例題實戰? 🎂

例題 1：912. 排序數組（中等）?

題目描述：給你一個整數數組 nums，請你將該數組升序排列。

?
示例：
輸入：nums = [5,2,3,1]?
輸出：[1,2,3,5]

代碼實現

class Solution {public int[] sortArray(int[] nums) {if (nums == null || nums.length <= 1) {return nums;}heapSort(nums);return nums;}private void heapSort(int[] arr) {int n = arr.length;// 構建最大堆for (int i = (n / 2) - 1; i >= 0; i--) {maxHeapify(arr, n, i);}// 排序階段for (int i = n - 1; i > 0; i--) {swap(arr, 0, i);maxHeapify(arr, i, 0);}}private void maxHeapify(int[] arr, int heapSize, int i) {int left = 2 * i + 1;int right = 2 * i + 2;int maxIndex = i;if (left < heapSize && arr[left] > arr[maxIndex]) {maxIndex = left;}if (right < heapSize && arr[right] > arr[maxIndex]) {maxIndex = right;}if (maxIndex != i) {swap(arr, i, maxIndex);maxHeapify(arr, heapSize, maxIndex);}}private void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
}

例題 2：215. 數組中的第 K 個最大元素（中等）?

題目描述：給定整數數組 nums 和整數 k，請返回數組中第 k 個最大的元素。?

示例：
輸入: [3,2,1,5,6,4] 和 k = 2?
輸出: 5

解題思路?

利用最大堆的堆頂為最大值的特性，彈出k-1個最大值后，堆頂即為第 k 個最大元素。或使用最小堆（更高效），維護大小為 k 的最小堆，堆頂為第 k 個最大元素。
方法 2（最小堆）Java 代碼

class Solution {public int findKthLargest(int[] nums, int k) {// 最小堆，堆頂為第k大元素PriorityQueue<Integer> minHeap = new PriorityQueue<>(k);for (int num : nums) {if (minHeap.size() < k) {minHeap.add(num); // 堆未滿，直接加入} else if (num > minHeap.peek()) {// 元素大于堆頂，替換堆頂并調整minHeap.poll();minHeap.add(num);}}return minHeap.peek(); // 堆頂為第k大元素}
}

復雜度分析?
時間復雜度：O (nlogk)，插入 n 個元素，每次堆調整為 O (logk)。?
空間復雜度：O (k)，堆存儲 k 個元素。
?

考研 408 例題解析? 🎂

例題 1：概念辨析題（選擇題）?

題目：下列關于堆的敘述中，正確的是（ ）。
?A. 最大堆中，從根節點到任意葉子節點的路徑上的元素是遞減的?
B. 堆排序是穩定的排序算法?
C. 構建最大堆的時間復雜度為 O (nlogn)?
D. 堆的調整操作（Heapify）的時間復雜度為 O (n)?

答案：A?
解析：?
A 正確：最大堆中，父節點的值大于等于子節點，因此根到葉子的路徑元素遞減。?
B 錯誤：堆排序中交換元素可能改變相等元素的相對順序（如 [2,2] 排序后可能顛倒），因此不穩定。?
C 錯誤：構建最大堆的時間復雜度為 O (n)，而非 O (nlogn)。?
D 錯誤：堆的調整操作時間復雜度為 O (logn)，與樹的高度相關。?

例題 2：算法設計題（408 高頻考點）?

題目：設計一個算法，利用堆實現一個優先級隊列，支持插入元素和提取最大元素操作，并分析兩種操作的時間復雜度。?

解題思路?
優先級隊列結構：用數組存儲堆，維護最大堆性質。?
插入操作：?
將新元素添加到堆尾。?
執行 “上浮” 操作：與父節點比較，若大于父節點則交換，直至根節點或小于父節點。?
提取最大元素操作：?
取出堆頂元素（最大值）。?
將堆尾元素移至堆頂。?
執行 “下沉” 操作（即堆調整），維護最大堆性質。

Java 代碼實現

public class MaxPriorityQueue {private int[] heap;private int size; // 當前元素個數private int capacity; // 隊列容量public MaxPriorityQueue(int capacity) {this.capacity = capacity;heap = new int[capacity + 1]; // 1-based索引，便于計算子節點size = 0;}// 插入元素public void insert(int val) {if (size == capacity) {throw new IllegalStateException("隊列已滿");}size++;heap[size] = val;swim(size); // 上浮調整}// 提取最大元素public int extractMax() {if (size == 0) {throw new NoSuchElementException("隊列為空");}int max = heap[1];swap(1, size); // 交換堆頂與堆尾size--;sink(1); // 下沉調整return max;}// 上浮操作（用于插入）private void swim(int k) {while (k > 1 && heap[k] > heap[k / 2]) { // 與父節點比較swap(k, k / 2);k = k / 2;}}// 下沉操作（用于提取最大元素）private void sink(int k) {while (2 * k <= size) { // 存在左子節點int j = 2 * k; // 左子節點if (j < size && heap[j] < heap[j + 1]) { // 右子節點更大j++;}if (heap[k] >= heap[j]) {break; // 已滿足最大堆性質}swap(k, j);k = j;}}private void swap(int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;}
}

復雜度分析?

插入操作：時間復雜度 O (logn)，上浮操作最多執行 logn 次（樹的高度）。?
提取最大元素：時間復雜度 O (logn)，下沉操作最多執行 logn 次。?

堆排序的擴展與應用? 🎂

實際應用場景?

優先級隊列：操作系統的進程調度、任務隊列等，需頻繁獲取最大值 / 最小值。?
Top-K 問題：如獲取海量數據中前 k 個最大元素（如 LeetCode 215 題）。?
流數據處理：實時處理數據流，維護動態數據的 Top-K 元素。?
堆排序：適用于大規模數據排序，尤其是內存有限的場景（原地排序）。?

與其他排序算法的對比

排序算法	平均時間復雜度	最壞時間復雜度	空間復雜度
堆排序	O(nlogn)	O(nlogn)	O(1)
快速排序	O(nlogn)	O(n2)	O(logn)
歸并排序	O(nlogn)	O(nlogn)	O(n)

考研 408 備考要點? 🎂

核心考點：堆的性質、堆的構建與調整、堆排序的步驟與復雜度。?

重點掌握：?

堆的索引計算（父節點與子節點的關系）。?
堆調整（Heapify）的遞歸與非遞歸實現。?
堆排序與優先級隊列的關聯，以及 Top-K 問題的解法。?

常見錯誤：?

混淆最大堆與最小堆的調整邏輯。?
構建堆時從 0 開始而非最后一個非葉子節點。?
忽略堆排序的不穩定性，錯誤認為其穩定。?

總結? 🎂

堆排序作為一種高效的排序算法，憑借 O (nlogn) 的穩定時間復雜度和原地排序的特性，在大規模數據處理中有著不可替代的地位。本文從堆的基本概念出發，詳細講解了堆的構建、調整操作和堆排序的完整流程，結合 LeetCode 例題（排序數組、Top-K 問題）展示了堆的核心應用，通過考研 408 例題解析了概念辨析和算法設計思路，并穿插 SVG 圖示直觀呈現了堆的結構與操作過程。?
掌握堆排序的關鍵在于：?
深刻理解堆的性質及索引映射關系。?
熟練實現堆的調整（Heapify）、構建和排序過程。?
靈活運用堆解決優先級隊列、Top-K 等實際問題。?
在考研備考中，堆的性質、堆排序的復雜度分析以及優先級隊列的實現是重點，需結合具體例題深入練習，理解堆在數據結構中的核心作用。