1. 算法思想

Flood Fill 問題的核心需求

給定一個二維網格（如像素矩陣）、一個起始坐標?(x, y)?和目標顏色?newColor，要求：

1. 將起始點?(x, y)?的顏色替換為?newColor。
2. 遞歸地將所有與起始點相鄰（上下左右）?且顏色與起始點原始顏色相同的區域，也替換為?newColor。

BFS 解決 Flood Fill 的算法思想

BFS 通過隊列實現 “逐層擴散”，步驟如下：

1. 記錄原始顏色，處理邊界情況

• 首先獲取起始點?(x, y)?的原始顏色?oldColor。
• 若?oldColor?與?newColor?相同，直接返回（無需填充，避免死循環）。

2. 初始化隊列，標記起始點

• 將起始點?(x, y)?加入隊列，作為 BFS 的起點。
• 立即將起始點的顏色更新為?newColor（或通過訪問標記記錄已處理，避免重復處理）。

3. 逐層擴散，填充相鄰區域

• 循環取出隊列中的節點?(x, y)，檢查其上下左右四個相鄰節點：
  • 若相鄰節點在網格范圍內（未越界）。
  • 且相鄰節點的顏色為?oldColor（與起始點原始顏色相同）。
• 則將該相鄰節點加入隊列，并立即更新其顏色為?newColor（或標記為已處理）。

4. 隊列清空，完成填充

• 當隊列中所有節點都處理完畢后，所有與起始點連通的?oldColor?區域已被替換為?newColor，算法結束。

示例：圖像著色（Flood Fill 經典場景）

假設有如下像素網格（oldColor=1，newColor=2，起始點?(1, 1)）：

[[1, 1, 0],[1, 1, 0],[0, 0, 1]
]

BFS 執行過程：

1. 起始點?(1,1)?入隊，顏色更新為?2，隊列：[(1,1)]。
2. 取出?(1,1)，檢查四鄰：
   • (0,1)?是?1?→ 入隊，更新為?2；隊列：[(0,1)]。
   • (2,1)?是?0?→ 跳過。
   • (1,0)?是?1?→ 入隊，更新為?2；隊列：[(0,1), (1,0)]。
   • (1,2)?是?0?→ 跳過。
3. 取出?(0,1)，檢查四鄰：
   • (0,0)?是?1?→ 入隊，更新為?2；隊列：[(1,0), (0,0)]。
   • 其他鄰點已處理或顏色不符，跳過。
4. 取出?(1,0)?和?(0,0)，檢查其鄰點，均無未處理的?1，隊列清空。
5. 最終結果（所有連通的?1?均變為?2）：

[[2, 2, 0],[2, 2, 0],[0, 0, 1]
]

關鍵邏輯解析

• 為什么用 BFS？：BFS 按 “距離起始點由近及遠” 的順序填充，適合需要 “逐層擴散” 的場景，且能保證所有連通區域被完整覆蓋。
• 避免重復處理：通過 “立即更新顏色為?newColor” 替代單獨的訪問標記數組，節省空間（因為?oldColor != newColor，已處理節點不會被再次加入隊列）。
• 邊界檢查：每次訪問鄰點前需判斷?x?和?y?是否在網格范圍內（0 ≤ x < 行數，0 ≤ y < 列數）。

算法復雜度

• 時間復雜度：O(n*m)，其中?n?為網格行數，m?為列數。每個單元格最多被訪問一次。
• 空間復雜度：O(n*m)，最壞情況下隊列需存儲所有單元格（如整個網格都是?oldColor?時）。

總結

BFS 解決 Flood Fill 的核心是用隊列管理待處理節點，逐層擴散并實時更新顏色，確保所有與起始點連通的相同顏色區域被高效、完整地填充。該思路直觀且易于實現，是處理連通區域填充問題的首選方法之一。

2. 例題

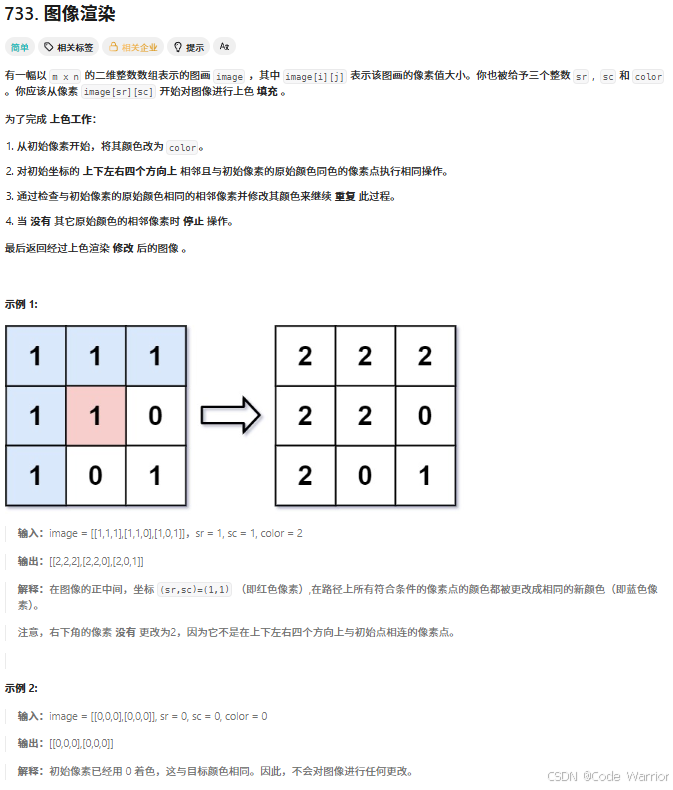
2.1 圖像渲染

733. 圖像渲染 - 力扣（LeetCode）

核心思路

1. 顏色檢查與預處理：

   • 獲取起始點?(sr, sc)?的原始顏色?prev。
   • 若?prev?與目標顏色?color?相同，直接返回原圖（避免重復填充）。

2. BFS 初始化：

   • 將起始點?(sr, sc)?加入隊列?q。
   • 獲取圖像的行數?n?和列數?m，用于邊界檢查。

3. 逐層擴散填充：

   • 循環處理隊列中的每個點，將其顏色替換為?color。
   • 檢查該點的上下左右四個相鄰點：
     • 若相鄰點在圖像范圍內且顏色等于?prev，將其加入隊列。
   • 隊列處理完畢后，所有連通的?prev?顏色區域均被替換為?color。

關鍵邏輯解析

1. 為什么用 BFS？
   BFS 按 “距離起始點由近及遠” 的順序處理節點，確保所有連通區域被完整覆蓋，且避免重復訪問。

2. 如何避免重復處理？
   當一個點被加入隊列時，立即將其顏色更新為?color。后續檢查相鄰點時，由于?image[x][y] == prev?的條件，已處理的點（顏色已變為?color）不會被重復加入隊列。

3. 邊界檢查的重要性
   x >= 0 && x < n && y >= 0 && y < m?確保不會越界訪問圖像。

示例演示

原圖（prev=1，color=2，起始點?(1, 1)）：

[[1, 1, 0],[1, 1, 0],[0, 0, 1]
]

BFS 執行過程：

1. 起始點?(1,1)?入隊，顏色更新為?2，隊列：[(1,1)]。
2. 處理?(1,1)，檢查四鄰：
   • (0,1)?顏色為?1?→ 入隊，更新為?2。
   • (1,0)?顏色為?1?→ 入隊，更新為?2。
   • 其他鄰點顏色為?0?或越界，跳過。
3. 處理?(0,1)，檢查四鄰：
   • (0,0)?顏色為?1?→ 入隊，更新為?2。
4. 處理?(1,0)?和?(0,0)，無符合條件的鄰點。
5. 隊列為空，處理結束，結果：

[[2, 2, 0],[2, 2, 0],[0, 0, 1]
]

復雜度分析

• 時間復雜度：O(n*m)，其中?n?和?m?分別為圖像的行數和列數。每個像素最多被訪問一次。
• 空間復雜度：O(n*m)，最壞情況下隊列可能存儲所有像素（如整個圖像顏色相同）。

總結

該算法通過 BFS 高效地實現了 Flood Fill，核心在于利用隊列逐層擴散并實時更新顏色以避免重復處理。這種方法簡潔直觀，適用于處理圖像連通區域的填充問題。

?

class Solution {// 表示x和y坐標typedef pair<int, int> PII;// 上下左右四個方向的偏移量int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};public:vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {int prev = image[sr][sc];if(prev == color) return image;queue<PII> q;q.push({sr, sc});int n = image.size(), m = image[0].size();while(q.size()){auto [x1, y1] = q.front();q.pop();image[x1][y1] = color; for(int i = 0; i < 4; ++i){int x = x1 + dx[i], y = y1 + dy[i];// 找到四個方向符合條件的位置if(x >= 0 && x < n && y >= 0 && y < m && image[x][y] == prev){q.push({x, y}); }}}return image;}
};

?

2.2 島嶼數量

200. 島嶼數量 - 力扣（LeetCode）

?

核心思路

1. 遍歷網格，尋找未訪問的陸地
   遍歷二維網格的每個單元格，當遇到值為?'1'（表示陸地）且未被訪問過（!vis[i][j]）的單元格時，說明發現了一個新的島嶼。

2. BFS 擴散標記整個島嶼
   對每個新發現的陸地單元格，啟動 BFS：

   • 將該單元格加入隊列，作為 BFS 的起點。
   • 從隊列中取出單元格，檢查其上下左右四個相鄰單元格：
     • 若相鄰單元格在網格范圍內（未越界）、值為?'1'?且未被訪問過，則將其加入隊列，并標記為已訪問（vis[x][y] = true）。
   • 此過程會遞歸遍歷完當前島嶼的所有相連陸地，確保整個島嶼被完整標記。

3. 計數島嶼數量
   每啟動一次 BFS，代表發現并處理了一個完整的島嶼，因此計數器（ret）加 1。最終計數器的值即為網格中島嶼的總數量。

關鍵邏輯解析

• vis?數組的作用：記錄已訪問的陸地單元格，避免重復統計同一島嶼的單元格。
• BFS 的優勢：通過隊列實現 “逐層擴散”，確保所有與起始點連通的陸地都被標記，高效覆蓋整個島嶼。
• 邊界檢查：通過?x >= 0 && x < n && y >= 0 && y < m?確保不訪問網格外的無效區域。

總結

算法通過遍歷網格發現新島嶼，利用 BFS 標記整個島嶼的所有陸地，最終統計島嶼數量。核心是用 BFS 實現連通區域的完整覆蓋和用訪問標記避免重復統計，時間復雜度為?O(n*m)（n、m?為網格行列數），每個單元格最多被訪問一次。

class Solution {typedef pair<int, int> PII;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int n, m;bool vis[300][300];public:int numIslands(vector<vector<char>>& grid) {int ret = 0;n = grid.size(), m = grid[0].size();for(int i = 0; i < n; ++i){for(int j = 0; j < m; ++j){if(grid[i][j] == '1' && !vis[i][j]){++ret;dfs(grid, i, j);}}}return ret;}void dfs(vector<vector<char>>& grid, int i, int j){queue<PII> q;q.push({i, j});while(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; ++k){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < n && y >= 0 && y < m && grid[x][y] == '1' && !vis[x][y]){q.push({x, y});vis[x][y] = true; }}}}
};

?

2.3 島嶼的最大面積

695. 島嶼的最大面積 - 力扣（LeetCode）

核心思路

1. 遍歷網格，尋找未訪問的陸地
   遍歷二維網格的每個單元格，當遇到值為?1（表示陸地）且未被訪問過（!vis[i][j]）的單元格時，說明發現了一個新的島嶼。

2. BFS 計算當前島嶼面積
   對每個新發現的陸地單元格，啟動 BFS 計算整個島嶼的面積：

   • 將該單元格加入隊列，標記為已訪問（vis[i][j] = true），初始化面積計數器（count = 1）。
   • 從隊列中取出單元格，檢查其上下左右四個相鄰單元格：
     • 若相鄰單元格在網格范圍內、值為?1?且未被訪問過，則將其加入隊列，標記為已訪問，并將面積計數器加 1。
   • 隊列處理完畢后，count?即為當前島嶼的面積。

3. 更新最大島嶼面積
   每次計算完一個島嶼的面積后，用當前面積更新全局最大面積（ret = max(ret, count)）。遍歷結束后，ret?即為網格中最大島嶼的面積。

關鍵邏輯解析

• vis?數組的作用：記錄已訪問的陸地單元格，避免重復計算同一島嶼的面積。
• BFS 的優勢：通過隊列實現 “逐層擴散”，完整覆蓋當前島嶼的所有陸地，確保面積計算準確。
• 面積統計：從起始單元格開始，每納入一個新的陸地單元格，面積計數器就加 1，最終得到整個島嶼的面積。

總結

算法通過遍歷網格發現新島嶼，利用 BFS 計算每個島嶼的面積，實時更新最大面積。核心是用 BFS 完整覆蓋連通區域以計算面積和用訪問標記避免重復統計，時間復雜度為?O(n*m)（n、m?為網格行列數），每個單元格最多被訪問一次。

?

class Solution {typedef pair<int, int> PII;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int vis[50][50];int n, m;int ret = 0;public:int maxAreaOfIsland(vector<vector<int>>& grid) {n = grid.size(), m = grid[0].size();for(int i = 0; i < n; ++i){for(int j = 0; j < m; ++j){if(grid[i][j] == 1 && !vis[i][j])dfs(grid, i, j);}}return ret;}void dfs(vector<vector<int>>& grid, int i, int j){queue<PII> q;q.push({i, j});vis[i][j] = true;int count = 1;while(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; ++k){int x1 = a + dx[k], y1 = b + dy[k];if(x1 < n && x1 >= 0 && y1 < m && y1 >= 0 && grid[x1][y1] == 1 && !vis[x1][y1]){++count;q.push({x1, y1});vis[x1][y1] = true;}}}ret = max(ret, count);}
};

?

2.4 被圍繞的區域

130. 被圍繞的區域 - 力扣（LeetCode）

核心思想

1. 遍歷網格，定位未訪問的 'O'
   遍歷整個網格，當遇到值為 'O' 且未被訪問（!vis[i][j]）的單元格時，啟動 BFS 處理該連通區域。

2. BFS 同步完成 “區域判斷” 與 “單元格記錄”
   在一次 BFS 中同時實現兩個目標：

   • 記錄區域所有單元格：用region數組存儲當前連通區域的所有 'O' 的坐標。
   • 判斷區域是否被包圍：通過hasEdge標記該區域是否包含邊緣單元格（位于網格邊界：x=0、x=n-1、y=0、y=m-1）。
     • 若區域包含邊緣單元格，hasEdge設為false（不被包圍）。
     • 若區域無邊緣單元格，hasEdge保持true（被完全包圍）。

3. 根據判斷結果處理區域
   BFS 結束后，若hasEdge為true（區域被包圍），則遍歷region數組，將所有記錄的 'O' 轉換為 'X'；否則不處理（保留邊緣連通區域）。

關鍵邏輯解析

• 合并 BFS 的優勢：避免兩次遍歷同一區域，一次 BFS 同時完成 “判斷” 和 “記錄”，減少冗余操作，時間復雜度優化為O(n*m)（n、m為網格行列數）。
• region數組的作用：臨時存儲當前區域的所有單元格，便于后續批量轉換，無需二次遍歷尋找目標單元格。
• hasEdge標記的作用：實時追蹤區域是否接觸網格邊緣，決定該區域是否需要被轉換為 'X'。

總結

算法通過一次 BFS 實現 “判斷區域是否被包圍” 和 “記錄待處理單元格”，最終根據判斷結果批量轉換被包圍區域。核心是用一次遍歷同步完成多任務，既保證邏輯清晰，又提高了效率，完美解決 “被圍繞的區域” 問題。

?

class Solution {typedef pair<int, int> PII;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int n, m;int vis[200][200];public:void solve(vector<vector<char>>& board) {n = board.size(), m = board[0].size();for(int i = 0; i < n; ++i){for(int j = 0; j  < m; ++j){if(board[i][j] == 'O' && !vis[i][j]){bfs(board, i, j);                  }}}}void bfs(vector<vector<char>>& board, int i, int j) // 判斷有沒有任何單元格位于 board 邊緣{bool hasEdge = true;if(i == 0 || i == n - 1 || j == 0 || j == m - 1){hasEdge = false;}vector<PII> region;queue<PII> q;q.push({i, j});region.push_back({i, j});vis[i][j] = true;while(q.size()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; ++k){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < n && y >= 0 && y < m && board[x][y] == 'O' && !vis[x][y]){vis[x][y] = true;if(x == 0 || x == n - 1 || y == 0 || y == m - 1){hasEdge = false;}q.push({x, y});region.push_back({x, y});}}}if(hasEdge){for(auto [x1, y1] : region)board[x1][y1] = 'X';}}
};

?