在醫療 AI 領域，很多分類任務具有有序類別的特性，如疾病嚴重程度（輕度→中度→重度）、腫瘤分級（G1→G2→G3）等。這類任務被稱為序數回歸（Ordinal Regression），需要特殊的損失函數設計。本文將深入解析序數回歸損失函數的原理及其實現代碼。

一、序數回歸與傳統分類的區別

傳統分類任務（如疾病類型識別）假設類別之間是無序的，而序數回歸的類別具有自然順序。例如：

• 疾病嚴重程度：0（正常）→1（輕度）→2（中度）→3（重度）
• 影像評分：1 分→2 分→3 分→4 分→5 分

對于這類任務，傳統的交叉熵損失存在局限性：它只關注類別預測的正確性，而忽略了類別之間的順序關系。例如，將真實標簽為 "中度"（2）的樣本預測為 "重度"（3），與預測為 "輕度"（1），在交叉熵損失中被視為同等錯誤，但實際上前者的錯誤程度更小。

二、序數回歸損失函數的核心思想

序數回歸損失函數的設計目標是：不僅要正確分類，還要保持類別之間的順序關系。常見的實現方法有以下幾種：

1. 累積概率模型：將序數分類轉化為一系列二分類問題
2. 相鄰類別比較：比較相鄰類別的預測概率
3. 距離敏感損失：懲罰與真實類別距離更遠的錯誤預測

代碼中實現的是累積概率模型，這是最常用的序數回歸方法之一。

三、累積概率模型的數學原理

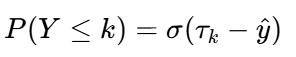累積概率模型的核心思想是：將序數類別轉化為一系列累積概率。對于有K個類別的問題，定義K-1個閾值cutspoints，，則樣本屬于類別k的概率為：，其中：

四、代碼實現解析

下面詳細解析序數回歸損失函數的實現代碼：

def ordinal_regression_loss(self, pred, label, num_classes, train_cutpoints=False, scale=20.0):# 1. 計算閾值（cutpoints）num_cutpoints = num_classes - 1#計算閾值數量cutpoints = torch.arange(num_cutpoints, device=pred.device).float() * scale / (num_classes - 2) - scale / 2cutpoints = nn.Parameter(cutpoints, requires_grad=train_cutpoints)# 2. 計算累積概率sigmoids = torch.sigmoid(cutpoints - pred)# 3. 構建概率矩陣：將累積概率轉換為每個類別的概率link_mat = sigmoids[:, 1:] - sigmoids[:, :-1]  # 中間類別的概率link_mat = torch.cat((sigmoids[:, [0]],         # 第一個類別的概率link_mat,                 # 中間類別的概率(1 - sigmoids[:, [-1]])   # 最后一個類別的概率), dim=1)# 4. 數值穩定性處理：防止對數計算時出現NaNeps = 1e-15likelihoods = torch.clamp(link_mat, eps, 1 - eps)# 5. 計算負對數似然損失neg_log_likelihood = torch.log(likelihoods)if label is None:loss = 0else:loss = -torch.gather(neg_log_likelihood, 1, label).mean()return loss, likelihoods

五、關鍵步驟詳解

1. 閾值（Cutpoints）計算

cutpoints = torch.arange(num_cutpoints, device=pred.device).float() * scale / (num_classes - 2) - scale / 2

• 作用：生成均勻分布的閾值點，將連續空間劃分為多個區間

例如：

• 
• 參數：
  • scale：控制閾值的范圍，默認 20.0
  • train_cutpoints：是否將閾值作為可訓練參數（默認為 False）
• 基礎序列torch.arange(num_cutpoints):對于K個類別,生成序列[0,1,2,...,K-2]
• 縮放因子：scale / (num_classes - 2)調整閾值之間的間隔
• 線性變換：* scale / (num_classes - 2) - scale / 2：將基礎序列映射到?[-scale/2, scale/2]?區間。

這兩行代碼的核心是將連續的預測空間均勻劃分為多個有序區間，每個區間對應一個類別。通過調整?scale?參數，可以控制區間的寬度，適應不同的任務需求。當?train_cutpoints=True?時，模型會在訓練過程中自動學習最優的閾值位置，進一步提升序數回歸的性能。

2. 累積概率計算

sigmoids = torch.sigmoid(cutpoints - pred)

• 作用：將模型預測值與閾值的差值通過 sigmoid 函數轉換為累積概率
• 示例：對于 3 個類別（2 個閾值），累積概率為：
• 

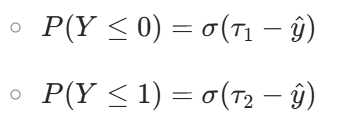
將模型輸出的抽象分數?pred，通過與閾值?cutpoints?的比較，轉換為 “屬于某個類別或更低等級” 的概率。這個概率越接近 1，說明?pred?越可能落在該類別或更低等級的區間里。

3. 類別概率矩陣構建

link_mat = sigmoids[:, 1:] - sigmoids[:, :-1]
link_mat = torch.cat((sigmoids[:, [0]], link_mat, 1 - sigmoids[:, [-1]]), dim=1)

• sigmoids[:, 1:]?→ 取所有樣本的第二個及以后的累積概率
• sigmoids[:, :-1]?→ 取所有樣本的第一個及以前的累積概率

4.數值穩定性處理：防止對數計算時出現NaN

在深度學習中，當計算概率的對數時（如交叉熵損失中的?log(p)），如果概率?p?非常接近 0（如 1e-20），會導致以下問題：

1. 數值下溢：計算機無法精確表示極小數，可能返回 0
2. 對數計算錯誤：log(0)?會返回負無窮（-inf）
3. 梯度爆炸：反向傳播時，-inf?的梯度會導致參數更新異常

同樣，當概率?p?接近 1 時，1-p?接近 0，也會引發類似問題。

• torch.clamp(input, min, max)?將輸入張量的每個元素限制在?[min, max]?范圍內
• 確保所有概率值在?[1e-15, 1-1e-15]?之間，避免過于接近 0 或 1

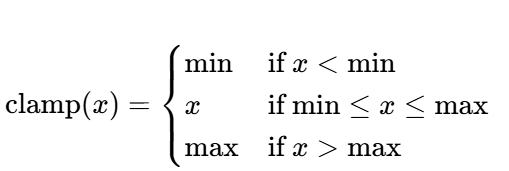
5. 負對數似然損失計算

neg_log_likelihood = torch.log(likelihoods)
loss = -torch.gather(neg_log_likelihood, 1, label).mean()

• 作用：計算每個樣本的真實類別對應的負對數概率，并取平均
• 

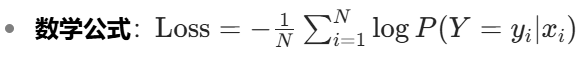
通過最大似然估計，讓模型預測的真實類別概率最大化。具體步驟為：

1. 計算對數似然：將概率轉換為對數空間
2. 按標簽選擇：提取真實類別對應的對數似然
3. 取負平均：轉換為損失（越小越好）

六、為什么選擇序數回歸損失？

在醫療分類任務中，序數回歸損失有以下優勢：

1. 利用順序信息：充分利用類別之間的順序關系，提高模型對程度差異的敏感性
2. 減少信息損失：相比將序數問題簡單視為分類問題，保留了更多結構信息
3. 更好的校準：輸出的概率具有更明確的臨床意義（如疾病嚴重程度的概率）
4. 提升性能：在序數分類任務中，通常比傳統分類損失取得更好的性能

七、實踐建議

1. 閾值初始化：

   • 代碼中的線性初始化是常用方法，但對于特定任務，可根據先驗知識自定義閾值
   • 當train_cutpoints=True時，模型會學習最優閾值位置

2. 模型輸出設計：

   • 模型最后一層應輸出單個連續值（而非類別概率），作為序數回歸的預測值
   • 可通過全連接層實現：nn.Linear(input_dim, 1)

3. 超參數調整：

   • scale參數影響閾值的分布范圍，需根據具體任務調整
   • 對于嚴重不平衡的序數類別，可考慮加權損失

4. 評估指標：

   • 除準確率外，建議使用 Kendall's τ 或 Spearman 相關性等評估順序一致性
   • 醫學場景中，還需關注不同嚴重程度類別的敏感性和特異性

八、總結

序數回歸損失函數為具有順序關系的醫療分類任務提供了更合適的優化目標。通過將類別轉化為累積概率，它不僅能正確分類，還能保持類別之間的順序關系，特別適合疾病嚴重程度分級、影像評分等醫療場景。

在實際應用中，可根據任務特點調整閾值初始化方式和損失函數參數，結合適當的評估指標，構建更符合臨床需求的醫療 AI 模型。