---

前言

回溯法就是暴力搜索，并不是什么高效的算法，最多再剪枝一下。

組合問題：N個數里面按一定規則找出k個數的集合
排列問題：N個數按一定規則全排列，有幾種排列方式
切割問題：一個字符串按一定規則有幾種切割方式
子集問題：一個N個數的集合里有多少符合條件的子集
棋盤問題：N皇后，解數獨等等

---

提示：以下是本篇文章正文內容，下面案例可供參考

一、組合問題

給定兩個整數 n 和 k，返回范圍 [1, n] 中所有可能的 k 個數的組合。
你可以按任意順序返回答案。

示例

• 輸入：n = 4, k = 2
• 輸出：
  [
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
  ]

通過for循環橫向遍歷，遞歸縱向遍歷，回溯不斷調整結果集

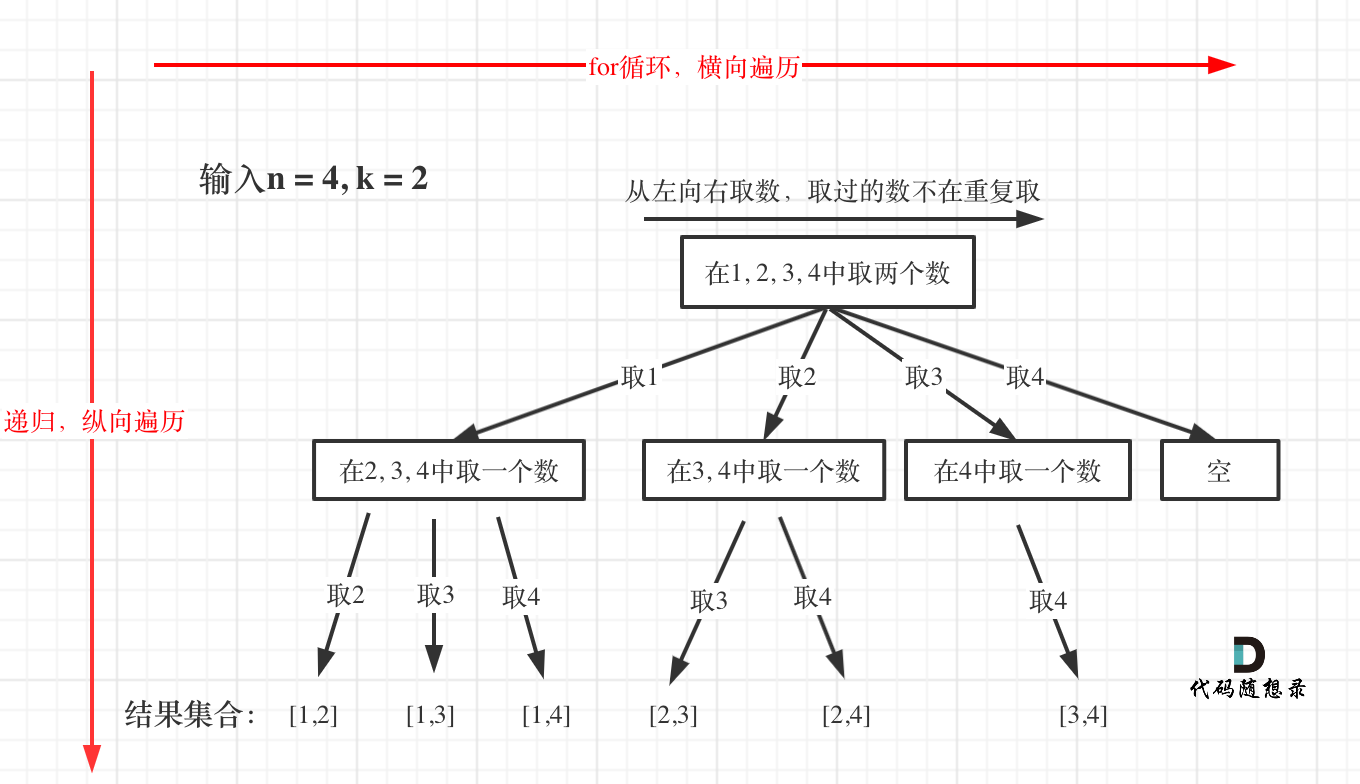
對于組合問題，什么時候需要startIndex，也需要考慮
如果是一個集合來求組合的話，就需要startIndex 216.組合總和III 、第77題. 組合
如果是多個集合求組和，各集合互相不影響，就不要startIndex17.電話號碼的字母組合

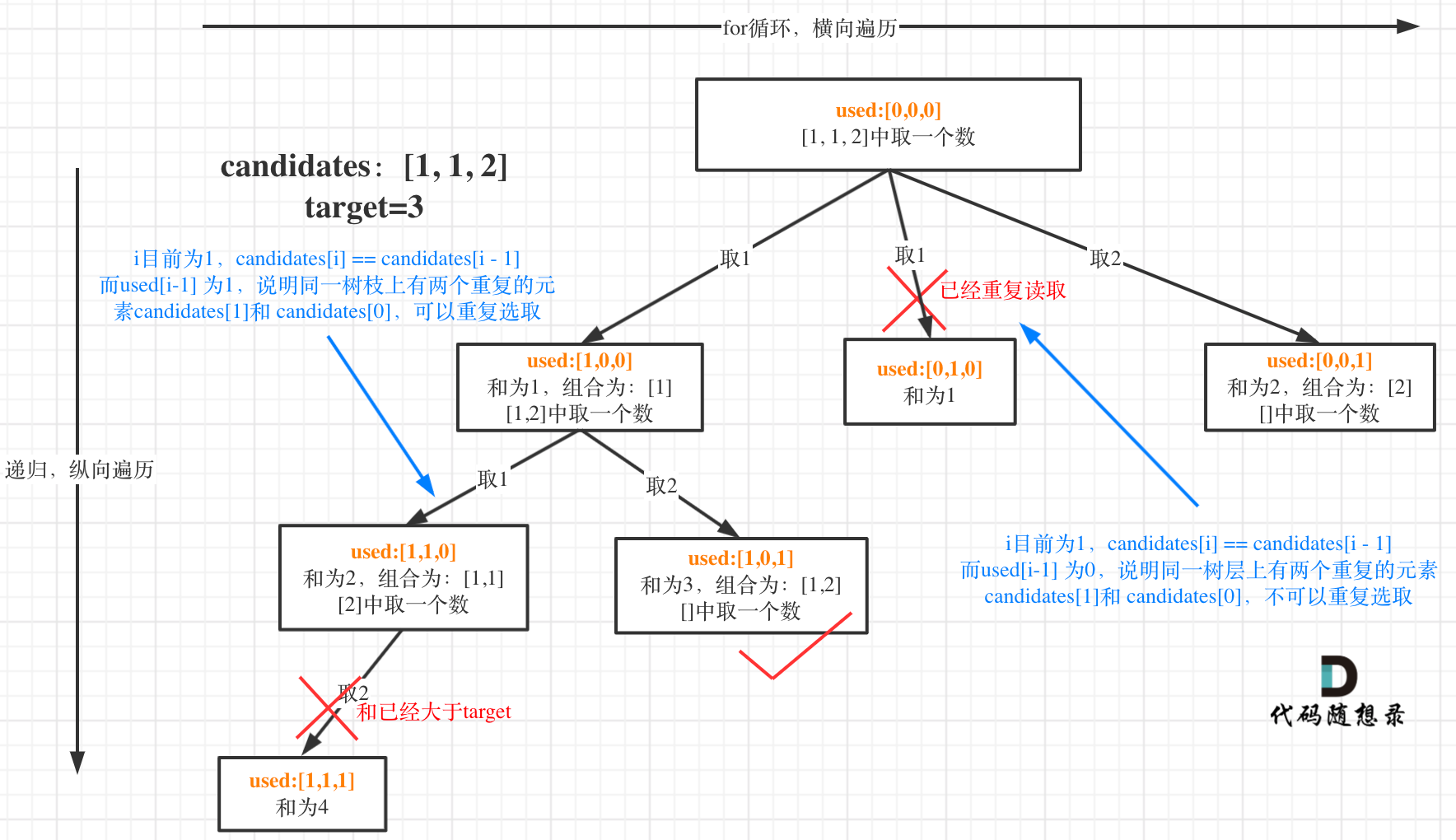
去重問題，樹枝去重和樹層去重，這里使用了used容器記錄遍歷情況。
used[i - 1] == true，說明同一樹枝該相同元素被使用過
used[i - 1] == false，說明同一樹層該相同袁術被使用過

二、切割問題

有如下幾個難點：

• 如何模擬切割線
• 切割問題中遞歸如何終止
• 在遞歸循環中如何截取子串
• 如何判斷回文

131.分割回文串
遞歸用來縱向遍歷，for循環用來橫向遍歷，切割線（就是圖中的紅線）切割到字符串的結尾位置，說明找到了一個切割方法。

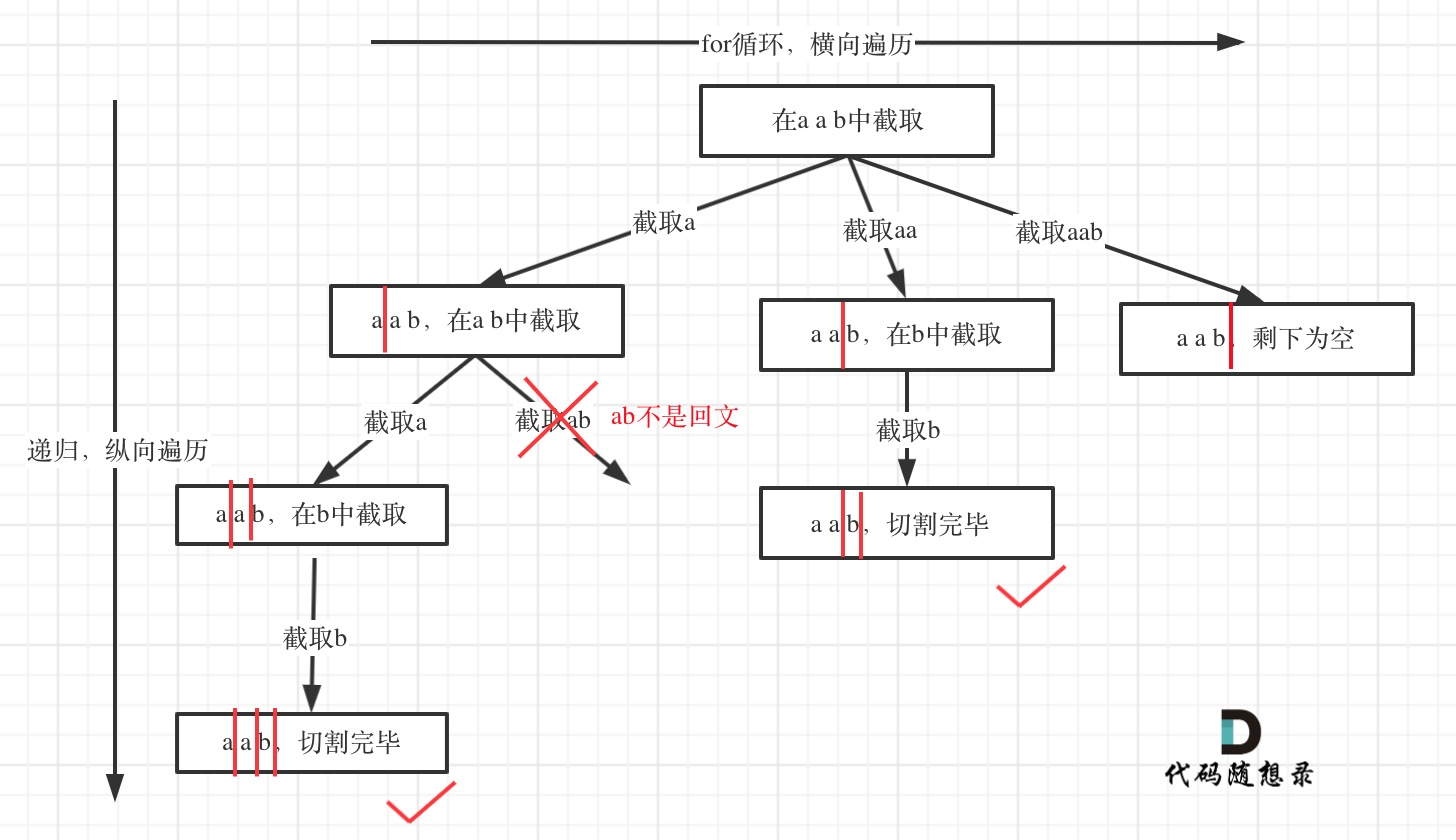
截取字符串
在for (int i = startIndex; i < s.size(); i++)循環中，我們 定義了起始位置startIndex，那么 [startIndex, i] 就是要截取的子串。

for (int i = startIndex; i < s.size(); i++) {if (isPalindrome(s, startIndex, i)) { // 是回文子串// 獲取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else {                // 如果不是則直接跳過continue;}backtracking(s, i + 1); // 尋找i+1為起始位置的子串path.pop_back();        // 回溯過程，彈出本次已經添加的子串
}

---

三、子集問題

在樹形結構中子集問題是要收集所有節點的結果，而組合問題是收集葉子節點的結果。

四、排列問題

排列是有序的，也就是說 [1,2] 和 [2,1] 是兩個集合，這和之前分析的子集以及組合所不同的地方。所以處理排列問題就不用使用startIndex了。

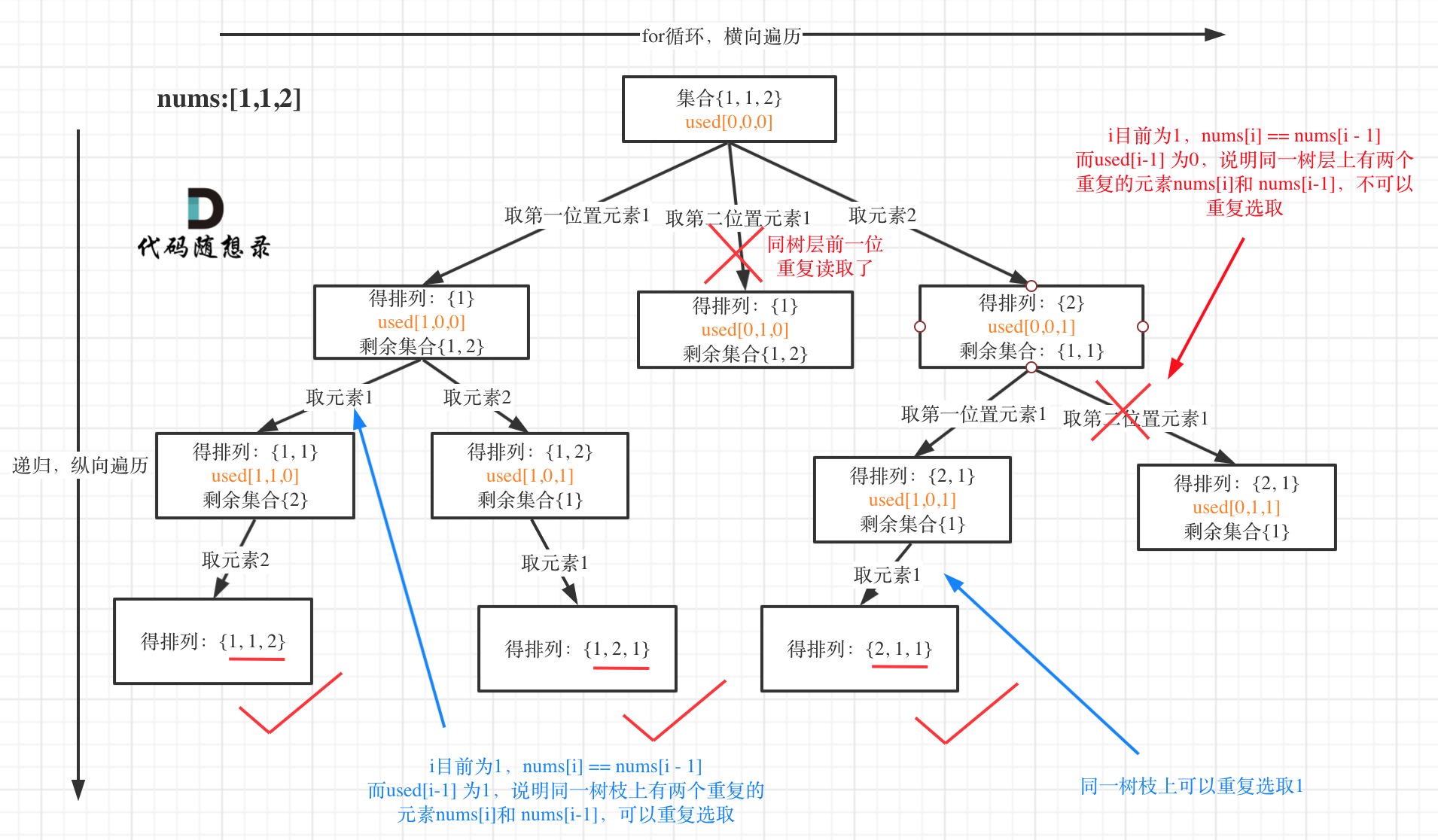
排列樹層上去重(used[i - 1] == false)，樹枝上去重（used[i - 1] == true）

五、性能分析

子集問題分析：

• 時間復雜度：O(2^{n)，因為每一個元素的狀態無外乎取與不取，所以時間復雜度為O(2}n)。
• 空間復雜度：O(n)，遞歸深度為n，所以系統棧所用空間為O(n)。每一層遞歸所用的空間都是常數級別。注意代碼里的result和path都是全局變量，就算是放在參數里，傳的也是引用，并不會新申請內存空間，最終空間復雜度為O(n)。

排列問題分析：

• 時間復雜度：O(n!)，這個可以從排列的樹形圖中很明顯發現，每一層節點為n，第二層每一個分支都延伸了n-1個分支，再往下又是n-2個分支，所以一直到葉子節點一共就是 n * (n-1) * (n-2) * … * 1 = n!。
• 空間復雜度：O(n)，和子集問題同理。

組合問題分析：

• 時間復雜度：O(2^n)，組合問題其實就是一種子集的問題，所以組合問題最壞的情況，也不會超過子集問題的時間復雜度。
• 空間復雜度：O(n)，和子集問題同理。

N皇后問題分析：

• 時間復雜度：O(n!)，其實如果看樹形圖的話，直覺上是O(n^n)，但皇后之間不能見面所以在搜索的過程中是有剪枝的，最差也就是O(n!)，n!表示n * (n-1) * … * 1。
• 空間復雜度：O(n)，和子集問題同理。

總結

提示：這里對文章進行總結：
例如：以上就是今天要講的內容，本文僅僅簡單介紹了pandas的使用，而pandas提供了大量能使我們快速便捷地處理數據的函數和方法。