1線性模型

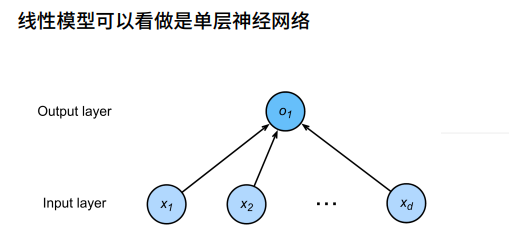
衡量預估質量

訓練數據

總結

2基礎優化方法

梯度下降是一種優化算法，常用于機器學習和深度學習中，用于最小化或最大化函數。在機器學習中，梯度下降通常用于最小化損失函數，以調整模型參數使其更好地擬合訓練數據。

梯度： 函數的梯度是該函數在某一點上的導數，表示函數在該點上的變化率。對于多變量函數，梯度是一個向量，指向函數在該點上變化最快的方向。

目標函數： 在機器學習中，我們通常有一個目標函數（也稱為損失函數），它是模型參數的函數，描述了模型預測與實際觀測之間的差距。

參數調整： 我們希望通過調整模型的參數來最小化目標函數。梯度下降的思想是沿著目標函數下降最快的方向進行參數調整。

度下降的步驟如下：

初始化參數： 隨機選擇初始參數值。
計算梯度： 計算目標函數對于當前參數的梯度。
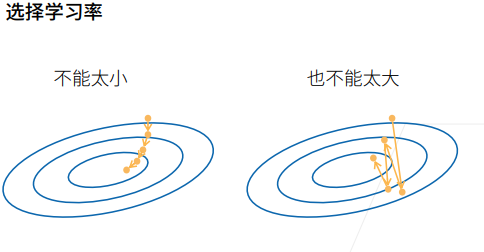
更新參數： 根據梯度的方向和大小來更新參數。通常使用學習率（learning rate）來控制更新步長。學習率不能太長也不能太小。
重復： 重復步驟2和步驟3，直到滿足停止條件，如達到最大迭代次數或梯度足夠小。
梯度下降有不同的變種，包括批量梯度下降（Batch Gradient Descent）、隨機梯度下降（Stochastic Gradient Descent）和小批量梯度下降（Mini-batch Gradient Descent）等。這些變種主要區別在于梯度的計算方式和參數更新的時機。

梯度下降是許多優化算法的基礎，它在機器學習領域得到廣泛應用，幫助模型學習適應復雜的數據模式。


小批量隨機梯度下降（Mini-batch Stochastic Gradient Descent，簡稱Mini-batch SGD）是梯度下降的一種變體，結合了批量梯度下降和隨機梯度下降的優點。在訓練過程中，Mini-batch SGD不是使用整個訓練數據集的梯度（批量梯度下降），也不是僅使用一個樣本的梯度（隨機梯度下降），而是使用一個小批量的樣本的梯度。

計算效率： 相較于批量梯度下降，Mini-batch SGD在計算梯度時不需要遍歷整個數據集，因此更加高效。與隨機梯度下降相比，使用小批量可以更好地利用硬件并行性，提高計算效率。

更穩定的更新： 相較于隨機梯度下降，Mini-batch SGD每次更新時使用多個樣本的平均梯度，能夠減小更新的方差，使得參數的更新更為穩定。

泛化性能： 由于小批量中包含了一定數量的樣本，因此Mini-batch SGD的參數更新更具有代表性，有助于提高模型的泛化性能

3 線性回歸從零開始實現

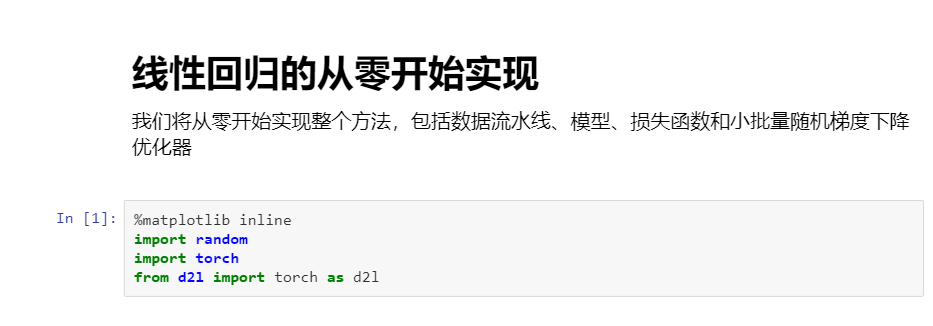
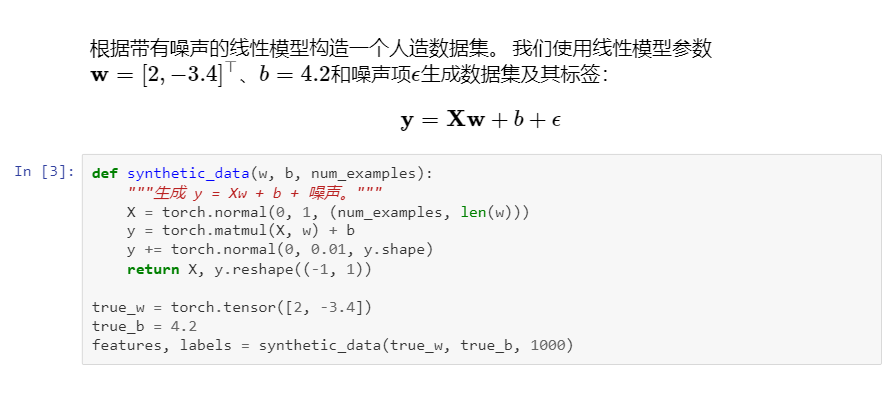
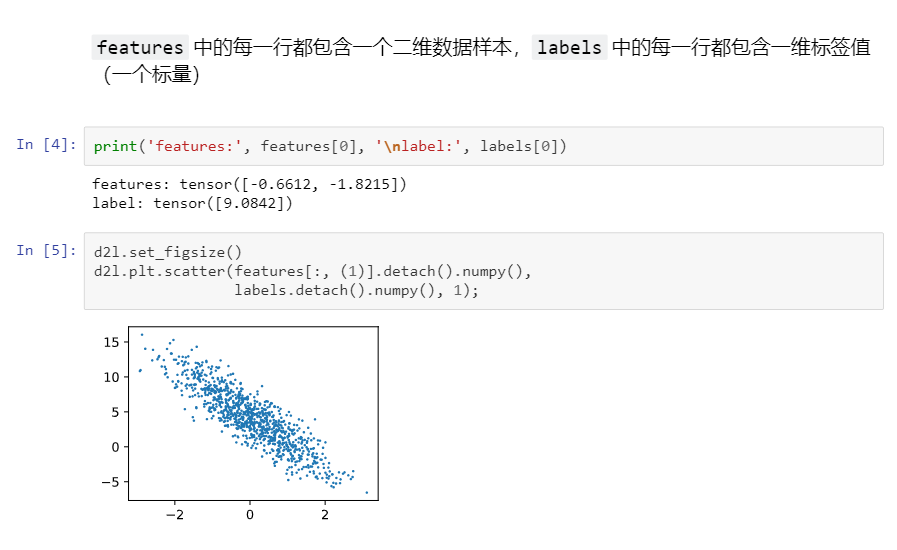
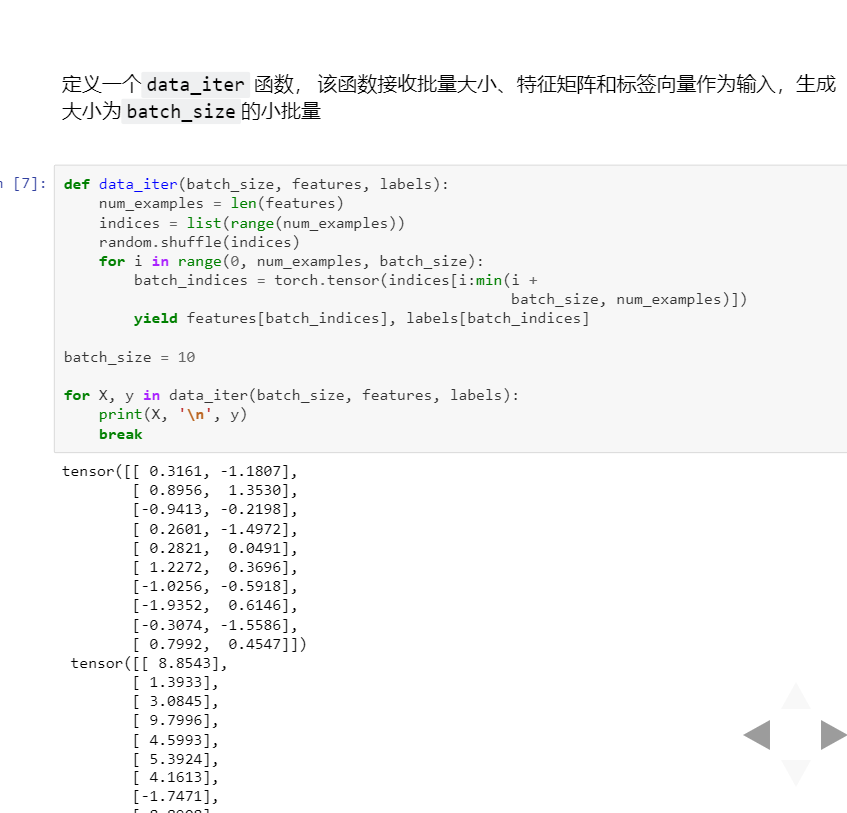
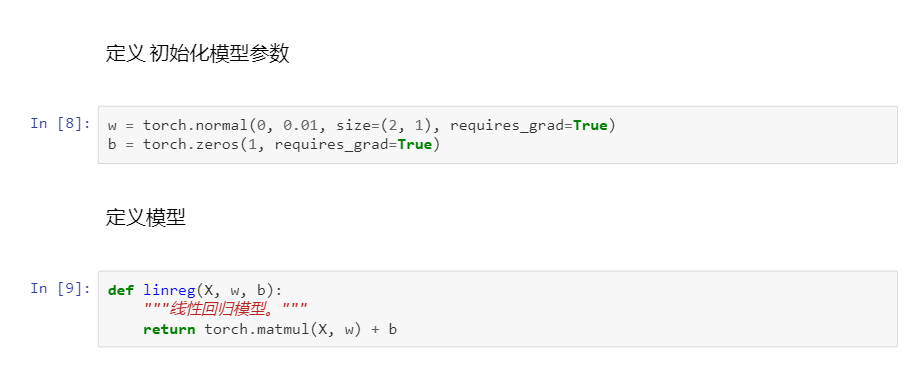
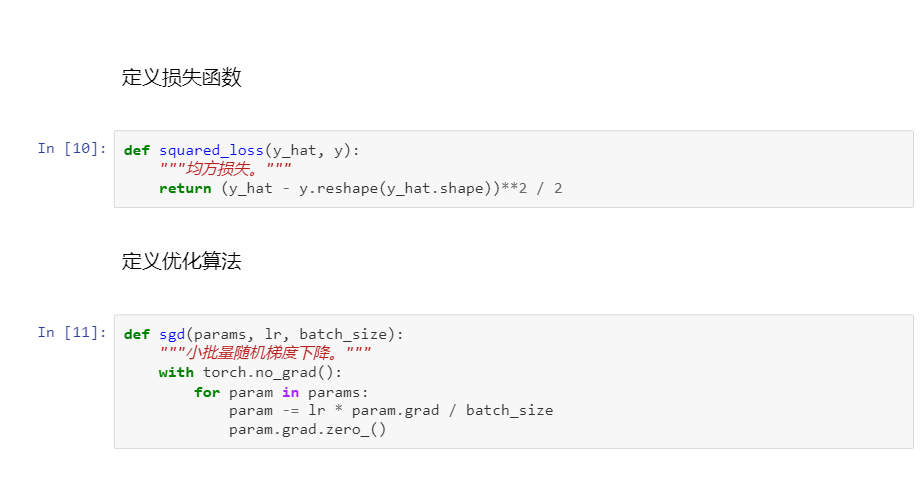
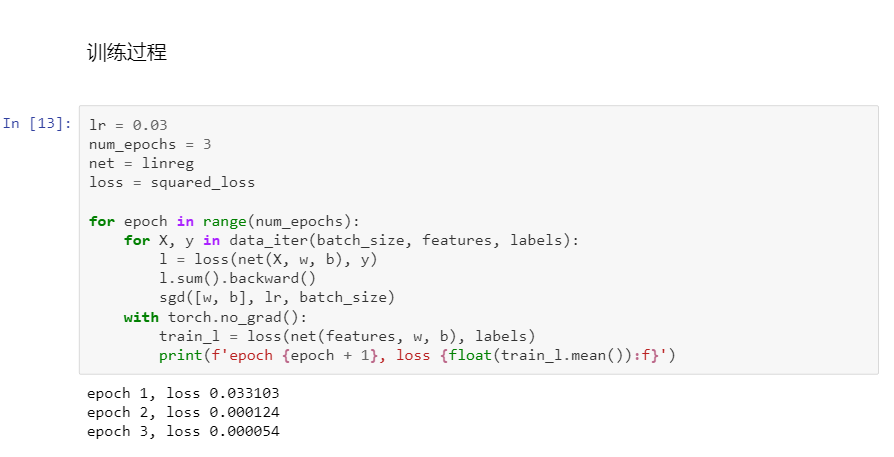
簡潔實現：