本系列持續更新Seurat單細胞分析教程，歡迎關注！

維度確定

為了克服 scRNA-seq 數據的任何單個特征中廣泛的技術噪音，Seurat 根據 PCA 分數對細胞進行聚類，每個 PC 本質上代表一個“元特征”，它結合了相關特征集的信息。因此，頂部主成分代表了數據集的穩健壓縮。但是，我們應該選擇包含多少個成分？ 10？ 20？ 100？

在 Macosko 等人中，我們實施了受 JackStraw 程序啟發的重采樣測試。雖然 Seurat 中仍然可用，但這是一個緩慢且計算成本高昂的過程，并且我們不再用于單細胞分析。

另一種啟發式方法生成“Elbow plot”：根據每個主成分解釋的方差百分比對主成分進行排名（ElbowPlot() 函數）。在此示例中，我們可以觀察到 PC9-10 周圍有一個“Elbow”，這表明大部分真實信號是在前 10 個 PC 中捕獲的。

ElbowPlot(pbmc)

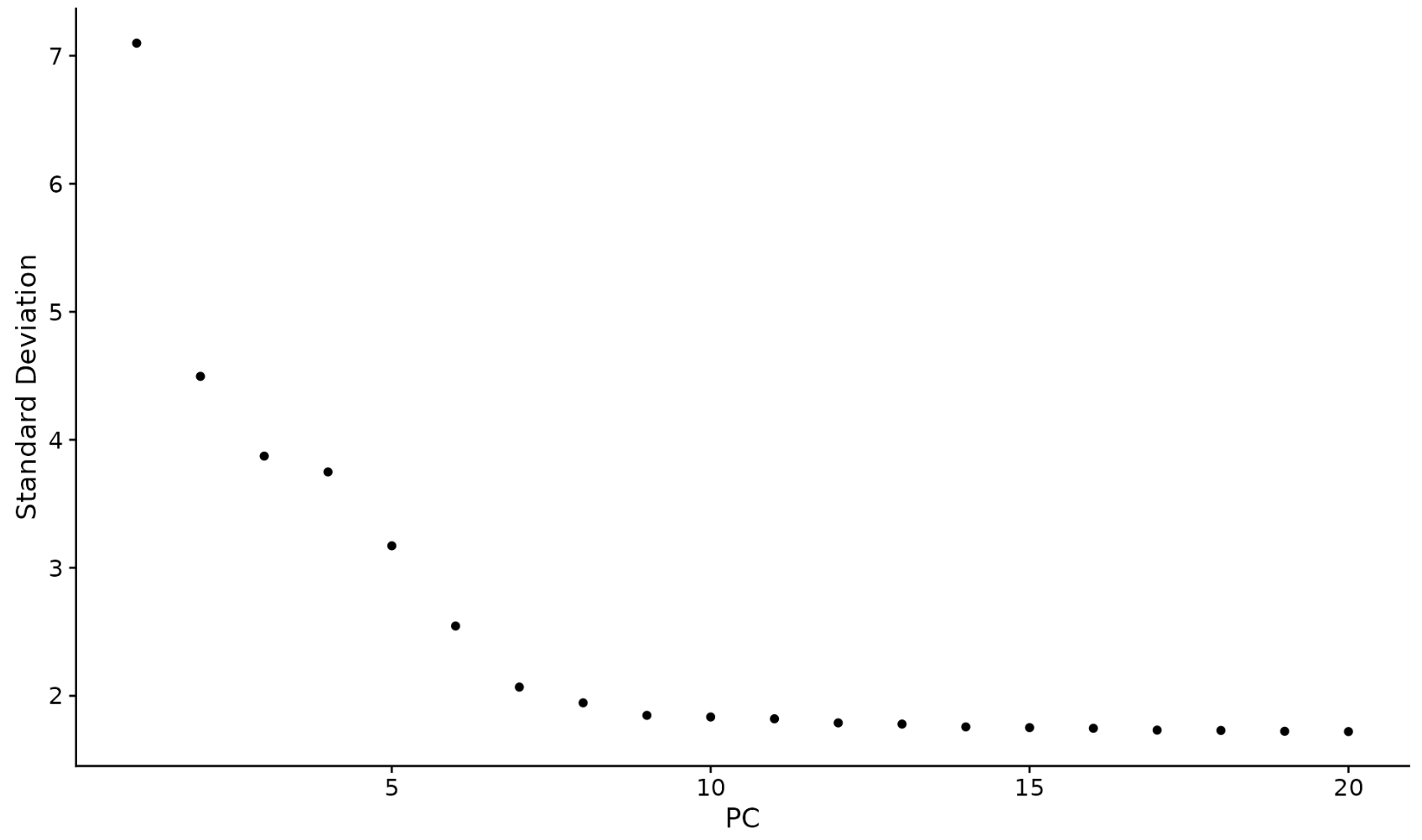
識別數據集的真實維度——對于用戶來說可能具有挑戰性/不確定性。因此，我們向用戶建議采用多種方法。第一個是更多的監督，探索 PC 以確定異質性的相關來源，并且可以與 GSEA 等結合使用。第二個（ElbowPlot） 第三個是常用的啟發式，可以立即計算。

在此示例中，我們可能選擇 PC 7-12 之間的任何值作為截止值。

我們在這里選擇了 10 個，但鼓勵用戶考慮以下事項：

• 樹突狀細胞和 NK 與 PC 12 和 13 密切相關的基因定義了罕見的免疫子集（即 MZB1 是漿細胞樣 DC 的標記）。然而，這些組非常罕見，在沒有先驗知識的情況下，很難將它們與這種大小的數據集的背景噪聲區分開來。
• 鼓勵用戶使用不同數量的 PC（10、15，甚至 50！）重復下游分析。
• 用戶在選擇該參數時偏高。例如，使用 5 PCs 執行下游分析會對結果產生重大不利影響，這將提醒用戶重新分析與思考。

細胞聚類

Seurat 應用基于圖的聚類方法，以（Macosko 等人）中的初始策略為基礎。重要的是，驅動聚類分析（基于先前識別的 PC）的距離度量保持不變。然而，我們將細胞距離矩陣劃分為簇的方法已得到顯著改進。

Seurat 的方法深受最近手稿的啟發，該手稿將基于圖的聚類方法應用于 scRNA-seq 數據和 CyTOF 數據 。簡而言之，這些方法將cell嵌入到圖結構中 - 例如 K 最近鄰 (KNN) 圖，在具有相似特征表達模式的cell之間繪制邊緣，然后嘗試將該圖劃分為高度互連的quasi-cliques’ 或 ‘communities’。

與 PhenoGraph 一樣，我們首先基于 PCA 空間中的歐氏距離構建 KNN 圖，并根據局部鄰域中的共享重疊（杰卡德相似度）細化任意兩個單元之間的邊緣權重。此步驟使用 FindNeighbors() 函數執行，并將先前定義的數據集維度（前 10 個 PC）作為輸入。

為了對cell進行聚類，我們接下來應用模塊化技術，例如 Louvain 算法（默認）或 SLM，迭代地將細胞分組在一起，目標是優化標準模塊化函數。 FindClusters() 函數實現此過程，并包含一個分辨率參數，用于設置下游聚類的“粒度”，增加的值會導致更多的聚類。我們發現，將此參數設置在 0.4-1.2 之間通常會為大約 3K 細胞的單細胞數據集帶來良好的結果。對于較大的數據集，最佳分辨率通常會增加。可以使用 Idents() 函數找到簇。

pbmc?<-?FindNeighbors(pbmc,?dims?=?1:10)
pbmc?<-?FindClusters(pbmc,?resolution?=?0.5)

##?Modularity?Optimizer?version?1.3.0?by?Ludo?Waltman?and?Nees?Jan?van?Eck
##?
##?Number?of?nodes:?2638
##?Number?of?edges:?95965
##?
##?Running?Louvain?algorithm...
##?Maximum?modularity?in?10?random?starts:?0.8723
##?Number?of?communities:?9
##?Elapsed?time:?0?seconds

#?Look?at?cluster?IDs?of?the?first?5?cells
head(Idents(pbmc),?5)

##?AAACATACAACCAC-1?AAACATTGAGCTAC-1?AAACATTGATCAGC-1?AAACCGTGCTTCCG-1?
##????????????????2????????????????3????????????????2????????????????1?
##?AAACCGTGTATGCG-1?
##????????????????6?
##?Levels:?0?1?2?3?4?5?6?7?8

未完待續，持續更新，歡迎關注！