名人說：莫道桑榆晚，為霞尚滿天。——劉禹錫（劉夢得，詩豪）
創作者：Code_流蘇(CSDN)（一個喜歡古詩詞和編程的Coder😊）

目錄

• • • • 1、重建二叉樹
      • • ①代碼實現（帶注釋）
        • ②補充說明（前序遍歷和中序遍歷重建二叉樹的原理）
      • 2、二叉樹的下一個結點
      • • ①代碼實現（帶注釋）
      • 3、用兩個棧實現隊列
      • • ①代碼實現（帶注釋）
        • ②補充說明（棧和隊列）
      • 4、斐波那契數列
      • • ①代碼實現（帶注釋）
        • ②補充說明（斐波那契數列）
      • 5、旋轉數組的最小數字
      • • ①代碼實現（帶注釋）
        • ②補充說明（二分搜索法）

1、重建二叉樹

原題鏈接：07.重建二叉樹

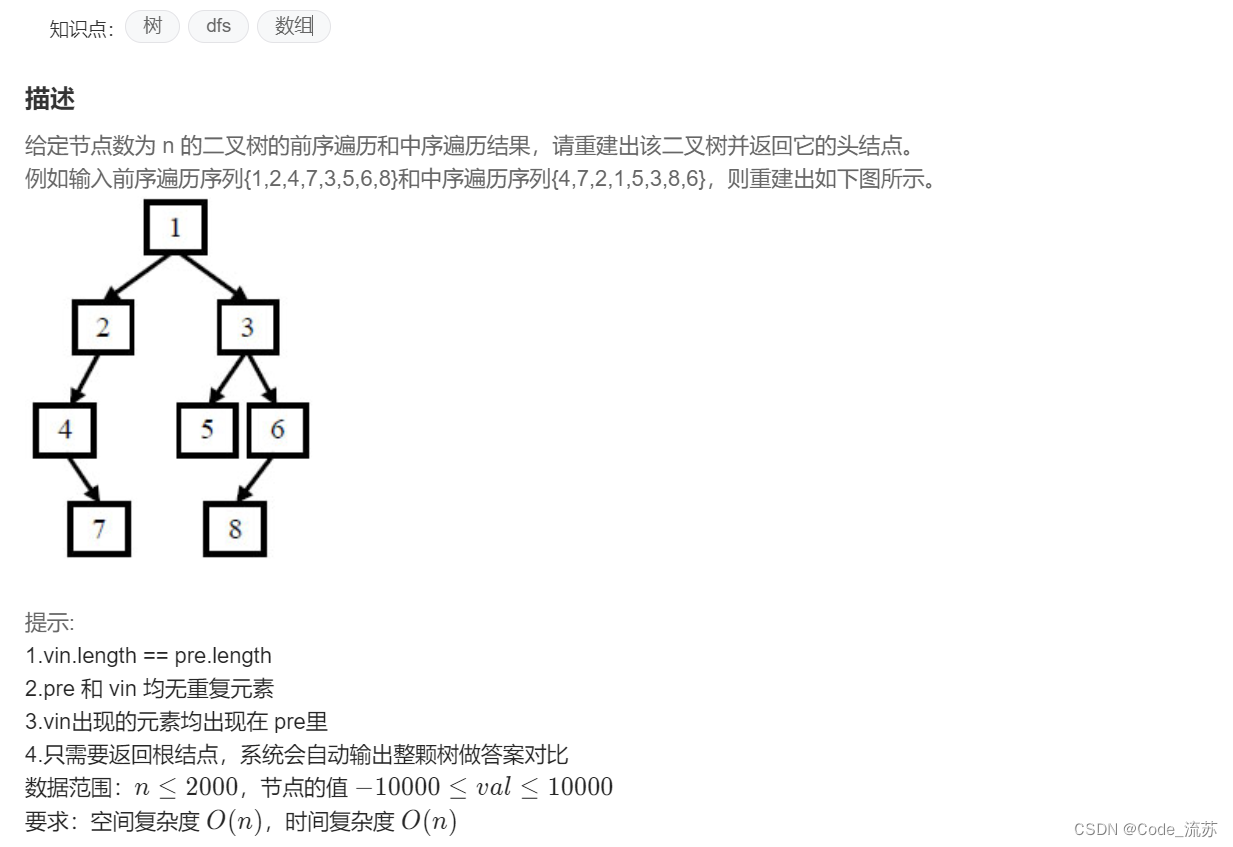
①代碼實現（帶注釋）

#include <unordered_map>
#include <vector>
/*** struct TreeNode {*  int val;*  struct TreeNode *left;*  struct TreeNode *right;*  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* };*/
/*解題關鍵：前序序列中的第一個元素總是樹的根。
通過這個根，我們可以在中序序列中找到根的索引位置。中序序列又總是被根索引分成兩部分：左子樹和右子樹。
同樣地，我們就能夠可以確定前序序列中左右子樹的邊界。最后通過遞歸這個過程來重建整棵樹即可解決問題。*/class Solution {public:unordered_map<int, int>indexMap; // 用于快速訪問中序遍歷中值的索引的映射TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder,int preorderStart, int preorderEnd, int inorderStart, int inorderEnd) {//若前序遍歷的起始位置大于結束位置               if (preorderStart > preorderEnd) {return nullptr; //若返回 nullptr ，表示該子樹不存在任何節點。}// 根據前序遍歷的特點，我們可以從前序遍歷獲取根節點值int rootVal = preorder[preorderStart]; // 創建原二叉樹的根節點TreeNode* root = new TreeNode(rootVal); // 在中序遍歷中找到根的索引下標int rootIndexInInorder = indexMap[rootVal]; // leftElements:左子樹中的元素數量int leftElements = rootIndexInInorder - inorderStart;// 遞歸構建左子樹root->left = buildTree(preorder, inorder, preorderStart + 1,preorderStart + leftElements, inorderStart, rootIndexInInorder - 1);// 遞歸構建右子樹root->right = buildTree(preorder, inorder, preorderStart + leftElements + 1,preorderEnd, rootIndexInInorder + 1, inorderEnd);//返回每次所構建子樹的根節點return root;}TreeNode* reConstructBinaryTree(vector<int>& preOrder, vector<int>& vinOrder) {int n = preOrder.size();// 填充indexMap以便快速訪問中序遍歷中的索引/*在重建二叉樹的過程中，需要頻繁地找到前序遍歷中的根節點在中序遍歷序列中的位置，這樣才能確定左右子樹的范圍，因此此處使用了映射。如果不使用映射，每次查找都可能需要遍歷整個中序遍歷序列來找到根節點的位置*/for (int i = 0; i < n; i++) {indexMap[vinOrder[i]] = i;}return buildTree(preOrder, vinOrder, 0, n - 1, 0, n - 1);}
};

②補充說明（前序遍歷和中序遍歷重建二叉樹的原理）

該題根據前序遍歷和中序遍歷重建二叉樹的原理是什么？

構建二叉樹的原理依賴于前序遍歷和中序遍歷的特性來確定樹的結構。前序遍歷的順序是根 左 右。中序遍歷的順序是左 根 右。

根據前序遍歷和中序遍歷構建二叉樹的步驟：

1. 確定根節點：在前序遍歷中，序列的第一個元素總是樹的根節點。

2. 劃分左右子樹：在中序遍歷中，根節點將序列分為兩部分，左邊是樹的左子樹，右邊是樹的右子樹。

3. 遞歸構建：利用上一步得到的左右子樹的中序遍歷序列，和從前序遍歷序列中提取相應的左右子樹序列，遞歸地重復上述過程構建整棵樹。

例如，假設有一棵樹的前序遍歷序列是 $[\text{A},\text{B},\text{D},\text{E},\text{C},\text{F}]$，中序遍歷序列是 $[\text{D},\text{B},\text{E},\text{A},\text{C},\text{F}]$：

1. 前序遍歷的第一個元素是 $A$，所以 $A$ 是根節點。

2. 在中序遍歷中，$A$ 前面的 $[\text{D},\text{B},\text{E}]$ 是左子樹的中序遍歷序列，$A$ 后面的 $[\text{C},\text{F}]$ 是右子樹的中序遍歷序列。

3. 遞歸構建左子樹和右子樹。

   • 對于左子樹，前序遍歷序列變為 $[\text{B},\text{D},\text{E}]$，中序遍歷序列是 $[\text{D},\text{B},\text{E}]$。重復上述步驟，可以構建出左子樹。
   • 對于右子樹，前序遍歷序列是 $[\text{C},\text{F}]$，中序遍歷序列是 $[\text{C},\text{F}]$。重復上述步驟，可以構建出右子樹。

通過這種方式，我們就可以準確地重建原始的二叉樹結構了。

2、二叉樹的下一個結點

原題鏈接：08.二叉樹的下一個結點

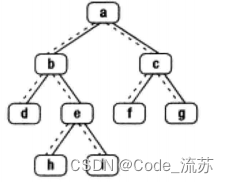
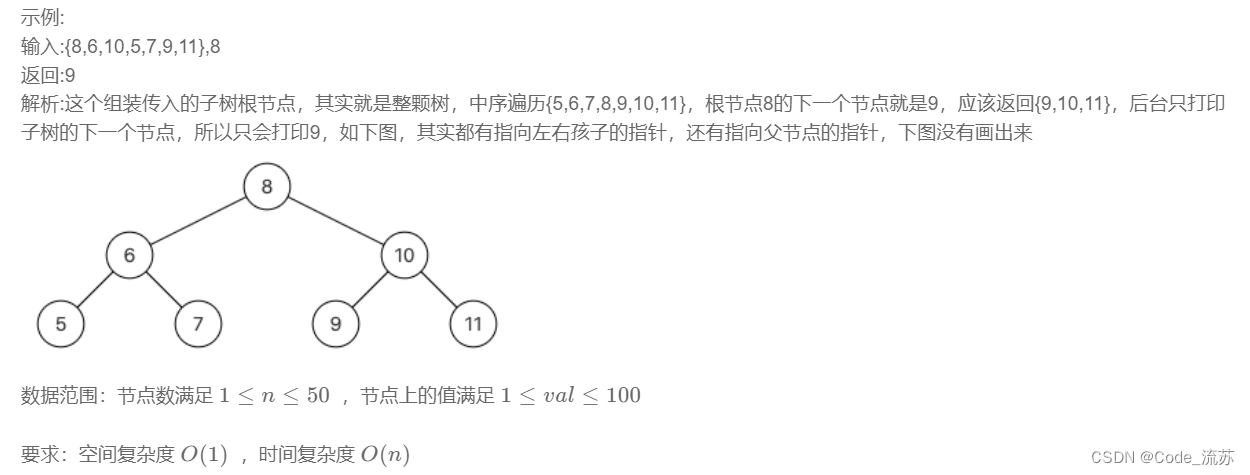
①代碼實現（帶注釋）

/*
struct TreeLinkNode {int val;struct TreeLinkNode *left;struct TreeLinkNode *right;struct TreeLinkNode *next;TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {}
};
*/
class Solution {public:// 定義樹節點指針向量nodes 用于存儲中序遍歷所有節點指針vector<TreeLinkNode*> nodes;// 獲取給定節點的下一個節點TreeLinkNode* GetNext(TreeLinkNode* pNode) {TreeLinkNode* root = pNode;// 循環遍歷找到根節點while (root->next) root = root->next;// 對樹進行中序遍歷，并將節點指針存儲在nodes向量中InOrder(root); int n = nodes.size(); // 獲取遍歷后得到的節點總數// 遍歷節點，查找給定節點的下一個節點for (int i = 0; i < n - 1; i++) {TreeLinkNode* cur = nodes[i];// 如果當前節點是給定節點if (pNode == cur) { // 則返回下一個節點return nodes[i +1]; }}// 若給定節點沒有下一個節點，則返回NULLreturn NULL; }// 中序遍歷二叉樹void InOrder(TreeLinkNode* root) {if (root == NULL) return;InOrder(root->left); // 遍歷左子樹//push_back函數可以在Vector向量最后添加一個元素（括號中的參數為要插入的值）nodes.push_back(root); // 訪問當前節點InOrder(root->right); // 遍歷右子樹}
};

3、用兩個棧實現隊列

原題鏈接：09.用兩個棧實現隊列

①代碼實現（帶注釋）

class Solution
{
public://使用兩個棧實現隊列的push操作void push(int node) {stack1.push(node); //直接將元素壓入stack1}//使用兩個棧實現隊列的pop操作int pop() {//如果stack2為空，則將stack1中的所有元素轉移到stack2中if (stack2.empty()) {while (!stack1.empty()) {//將stack1的棧頂元素壓入stack2stack2.push(stack1.top());//刪除stack1的棧頂元素stack1.pop();}}//如果stack2不為空，則直接從stack2中彈出棧頂元素，即隊頭元素//獲取stack2的棧頂元素int head = stack2.top(); //刪除stack2的棧頂元素stack2.pop();//返回隊頭元素return head;}private:stack<int> stack1;//棧1用于插入操作stack<int> stack2;//棧2用于刪除操作
};

②補充說明（棧和隊列）

棧（Stack）和隊列（Queue）是兩種基本的數據結構，它們在處理數據的方式上有著本質的區別：

• 棧 是一種后進先出的數據結構。
  最后添加進棧的元素將是第一個被移除的。想象一下一疊盤子，你只能從頂部添加或移除盤子。常見的操作包括“push”（添加一個元素到棧頂）和“pop”（移除棧頂元素）。

• 隊列 是一種先進先出的數據結構。
  第一個添加進隊列的元素將是第一個被移除的。可以想象成在銀行排隊，新來的顧客排在隊伍的末尾，而服務員從隊伍的前端開始服務顧客。常見的操作包括“enqueue”（將一個元素添加到隊列末尾）和“dequeue”（移除隊列前端的元素）。

4、斐波那契數列

原題鏈接：10. 斐波那契數列

①代碼實現（帶注釋）

class Solution {
public:/*** 代碼中的類名、方法名、參數名已經指定，請勿修改，直接返回方法規定的值即可** * @param n int整型 * @return int整型*/int Fibonacci(int n) {//處理邊界情況if(n <= 1)return n;//初始化前兩個斐波那契數	int a=0,b=1;//計算第n項for(int i = 2; i <= n; i++){//更新斐波那契數到第n項int next = a+b;a = b;b = next;}//第n項的斐波那契數列return b;}
};

②補充說明（斐波那契數列）

斐波那契數列是一種在數學和計算機科學中廣泛應用的數列。它由以下遞歸關系定義：每個數是前兩個數的和，其最初兩個數通常定義為 $F(0)=0,F(1)=1$。因此，斐波那契數列的開始部分是：

$$0,1,1,2,3,5,8,13,21,34,\dots$$

形式上，斐波那契數列可以用數學公式表示為：

$$F(n)=F(n?1)+F(n?2)$$

其中，$n\ge 2$ 且 $F(0)=0$, $F(1)=1$。

特點：除了最開始的兩個數字外，每個數字都是其前兩個數字的和。

5、旋轉數組的最小數字

原題鏈接：11. 旋轉數組的最小數字

①代碼實現（帶注釋）

class Solution {
public:/*** 代碼中的類名、方法名、參數名已經指定，請勿修改，直接返回方法規定的值即可** * @param nums int整型vector * @return int整型*//*由于數組原本是非降序排列的，旋轉后，數組被分成兩個非降序的子數組。最小值是這兩個子數組的分界點。 因此我們可以使用二分搜索法/折半查找法來優化搜索過程，這樣時間復雜度就是O(logn)。*/ int minNumberInRotateArray(vector<int>& nums) {//如果數組為空，返回-1if(nums.empty()) return -1; //定義左側left位置為0int left = 0;//右側right位置為n-1int right = nums.size() - 1;//如果旋轉數組沒有旋轉（例如[1,2,3,4,5]變成[1,2,3,4,5]），直接返回第一個元素if(nums[left] < nums[right]){return nums[left];}//二分查找while (left < right) {int mid = left + (right - left) / 2;if(nums[mid] > nums[right]){//[mid+1,right]區間left = mid + 1;}else if (nums[mid] < nums[right]) {//[left,mid]區間right = mid;}else {//當中間值和右邊值相等時，縮小范圍right--;}}//循環結束，此時left == right，指向的就是數組中的最小值return nums[left];}
};

②補充說明（二分搜索法）

二分搜索法（Binary Search）是一種在有序數組中查找特定元素的高效算法。

原理：將待搜索的數組分成兩半，然后根據中間元素與目標值的比較結果來確定下一步搜索的區域，從而逐步縮小搜索范圍，直到找到目標值或確定目標值不存在。

二分搜索的基本步驟如下：

1. 確定搜索區間：初始搜索區間為整個數組。
2. 找到中間元素：計算搜索區間的中點位置，取出中間元素進行比較。
3. 比較中間元素與目標值：
   • 如果中間元素正好等于目標值，則搜索成功。
   • 如果中間元素小于目標值，則將搜索區間調整為中間元素右側的子區間，繼續搜索。
   • 如果中間元素大于目標值，則將搜索區間調整為中間元素左側的子區間，繼續搜索。
4. 重復步驟2和3，直到找到目標值或搜索區間為空（表示目標值不存在于數組中）。

二分搜索的效率較高，其時間復雜度為 $O(\log n)$，其中 $n$ 是數組的長度。因此本題采用二分搜索法，可以幫助我們在查找數據時節省大量的時間。

很感謝你能看到這里，如有相關疑問，還請下方評論留言。
Code_流蘇(CSDN)（一個喜歡古詩詞和編程的Coder😊）
如果大家喜歡的話，請動動手點個贊和關注吧，非常感謝你們的支持！