1.個體與集成

????????集成學習通過將多個學習器進行結合,常可獲得比單一學習器顯著優越的泛化性能，這對“弱學習器”(weak learner)尤為明顯因此集成學習的很多理論研究都是針對弱學習器進行的而基學習器有時也被直接稱為弱學習器。

????????要獲得好的集成個體學習器應“好而不同”，即個體學習器要有一定的“準確性”，即學習器
不能太壞，并且要有“多樣性”(diversity)，即學習器間具有差異?

2.Boosting? ? ? ???

????????Boosting是一族可將弱學習器提升為強學習器的算法，這族算法的工作機制類似: 先從初始訓練集訓練出一個基學習器,再根據基學習器的表現對訓練樣本分布進行調整,使得先前基學習器做錯的訓練樣本在后續受到更多關注，然后基于調整后的樣本分布來訓練下一個基學習器: 如此重復進行直至基學習器數目達到事先指定的值 T，最終將這T個基學習器進行加權結合

????????Boosting算法要求基學習器能對特定的數據分布進行學習,這可通過“重賦權法”(re-weighting)實施，即在訓練過程的每一輪中，根據樣本分布為每個訓練樣本重新賦予一個權重.

????????對無法接受帶權樣本的基學習算法,則可通過“重采樣法”(resampling)來處理，即在每一輪學習中根據樣本分布對訓練集重新進行采樣,再用重采樣而得的樣本集對基學習器進行訓練.

????????一般而言,這兩種做法沒有顯著的優劣差別.需注意的是，若采用“重采樣法”，則可獲得“重啟動”機會以避免訓練過程過早停止[Kohavi and Wolpert,1996]，即在拋棄不滿足條件的當前基學習器之后，可根據當前分布重新對訓練樣本進行采樣,再基于新的采樣結果重新訓練出基學習器從而使得學習過程可以持續到預設的T輪完成。

????????從偏差-方差分解的角度看,Boosting 主要關注降低偏差，因此Bosting能基于泛化性能相當弱的學習器構建出很強的集成。

3.Bagging與隨機森林??

（1）Bagging? ??

????????Bagging是針對于樣本而言的，它直接基于自助采樣法(bootstrap sampling)，給定包含 m個樣本的數據集我們先隨機取出一個樣本放入采樣集中，再把該樣本放回初始數據集,使得下次采樣時該樣本仍有可能被選中,這樣,經過 m次隨機采樣操作,我們得到含 m個樣本的采樣集初始練集中有的樣本在采樣集里多次出現，有的則從未出現由式(2.1)可知初始訓練集中約有 63.2%的樣本出現在采樣集中
????????照這樣,我們可采樣出T個含 m 個訓練樣本的采樣集然后基于每個采樣集訓練出一個基學習器,再將這些基學習器進行結合.這就是 Bagging 的基本流程在對預測輸出進行結合時,Bagging 通常對分類任務使用簡單投票法,對回歸任務使用簡單平均法.若分類預測時出現兩個類收到同樣票數的情形，則最簡單的做法是隨機選擇一個,也可進一步考察學習器投票的置信度來確定最終勝者。

????????與標準 AdaBoost 只適用于二分類任務不同,Bagging 能不經修改地用于多分類、回歸等任務

????????值得一提的是，自助采樣過程還給Bagging 帶來了另一個優點:由于每個基學習器只使用了初始訓練集中約 63.2%的樣本，剩下約 36.8%的樣本可用作驗證集來對泛化性能進行“包外估計”。

????????包外樣本還有許多其他用途，例如當基學習器是決策樹時，可使用包外樣本來輔助剪枝,或用于估計決策樹中各結點的后驗概率，以輔助對零訓練樣本結點的處理:當基學習器是神經網絡時可使用包外樣本來輔助早期停止，以減小過擬合風險.?

????????從偏差-方差分解的角度看,Bagging 主要關注降低方差，因此它在不剪枝決策樹、神經網絡等易受樣本擾動的學習器上效用更為明顯。

(2) 隨機森林

? ? ? ? 隨機森林是針對屬性而言的，對基決策樹的每個結點,先從該結點的屬性集合中隨機選擇一個包含k個屬性的子集，然后再從這個子集中選擇一個最優屬性用于劃分.這里的參數k 控制了隨機性的引入程度: 若令 k =d則基決策樹的構建與傳統決策樹相同，若令k =1,則是隨機選擇一個屬性用于劃分;一般情況下,推薦值 k = log2 d

????????隨機森林對 Bagging 只做了小改動,但是與 Bagging 中基學習器的“多樣性，僅通過樣本擾動(通過對初始訓練集采樣)而來不同,隨機森林中基學習器的多樣性不僅來自樣本擾動,還來自屬性擾動,這就使得最終集成的泛化性能可通過個體學習器之間差異度的增加而進一步提升.

4.結合策略

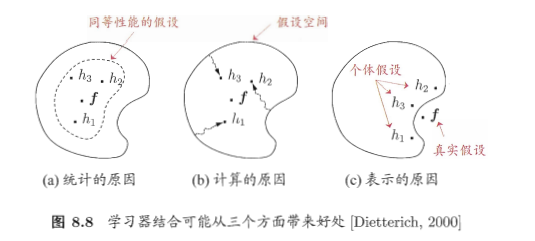
????????學習器結合可能會從三個方面帶來好處:

• 首先，從統計的方面來看，由于學習任務的假設空間往往很大,可能有多個假設在訓練集上達到同等性能,此時若使用單學習器可能因誤選而導致泛化性能不佳,結合多個學習器則會減小這一風險;
• 第二，從計算的方面來看,學習算法往往會陷入局部極小，有的局部極小點所對應的泛化性能可能很糟糕，而通過多次運行之后進行結合,可降低陷入糟糕局部極小點的風險;
• 第三,從表示的方面來看,某些學習任務的真實假設可能不在當前學習算法所考慮的假設空間中，此時若使用單學習器則肯定無效,而通過結合多個學習器，由于相應的假設空間有所擴大有可能學得更好的近似圖? ? ??

?????????

? ? （1）平均法

????????????????? ? ? ? ? ??

?

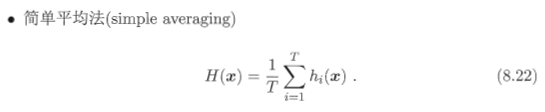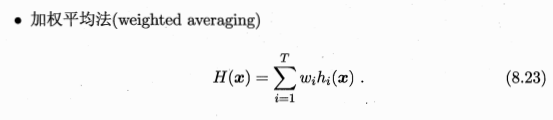????????加權平均法的權重一般是從訓練數據中學習而得,現實任務中的訓練樣本通常不充分或存在噪聲，這將使得學出的權重不完全可靠，尤其是對規模比較大的集成來說,要學習的權重比較多,較容易導致過擬合.因此,實驗和應用均顯示出加權平均法未必一定優于簡單平均法，一般而言在個體學習器性能相差較大時宜使用加權平均法,而在個體學習器性能相近時宜使用簡單平均法?

（2）投票法

• 絕對多數投票法(majority voting)：即若某標記得票過半數，則預測為該標記;否則拒絕預測
• 相對多數投票法(plurality voting)：即預測為得票最多的標記,若同時有多個標記獲最高票，則從中隨機選取一個
• 加權投票法(weightedvoting)? ? ? ???

?

????????標準的絕對多數投票法(8.24)提供了“拒絕預測”選項，這在可靠性要求較高的學習任務中是一個很好的機制，但若學習任務要求必須提供預測結果，則絕對多數投票法將退化為相對多數投票法.因此,在不允許拒絕預測的任務中,絕對多數、相對多數投票法統稱為“多數投票法”?

考慮輸出類型：?

????????

????????????????

?（3）學習法

????????Stacking先從初始數據集訓練出初級學習器，然后“生成”一個新數據集用于訓練次級學習器.在這個新數據集中,初級學習器的輸出被當作樣例輸入特征，而初始樣本的標記仍被當作樣例標記????????

? ? ? ? 需要注意的是，次級訓練集的生成并不是基于初始的訓練集，使用訓練集生成很容易導致過擬合。而是采用k折交叉驗證的方式，使用驗證集的輸出作為次級訓練集。?

????????次級學習器的輸入屬性表示和次級學習算法對 Stacking集成的泛化性能有很大影響.有研究表明，將初級學習器的輸出類概率作為次級學習器的輸入屬性，用多響應線性回歸(Multi-response Linear Regression,簡稱MLR)作為次級學習算法效果較好[Ting and Witten,1999],在MLR中使用不同的屬性集更佳[Seewald,2002]

????????貝葉斯模型平均(Bayes Model Averaging,簡稱 BMA)基于后驗概率來為不同模型賦予權重,可視為加權平均法的一種特殊實現.[Clarke,2003] 對Stacking 和 BMA 進行了比較，理論上來說，若數據生成模型恰在當前考慮的模型中且數據噪聲很少，則 BMA 不差于 Stacking; 然而在現實應用中無法確保數據生成模型一定在當前考慮的模型中，甚至可能難以用當前考慮的模型來進行近似，因此Stacking 通常優于 BMA因為其魯棒性比 BMA 更好而且BMA對模型近似誤差非常敏感

5.多樣性?

（1）誤差——分歧分解

? ? ? ? 通過數學推導可以得到模型泛化誤差、基學習器的泛化誤差、個體分歧值之間的關系：

?????????

? ? ? ?欲構建泛化能力強的集成,個體學習器應“好而不同，事實個體學習的“準確”性“多樣性”本身就在沖突.一般的,準確性很高之后,要增加多樣性就需犧牲準確性.?

（2）多樣性度量

???

（3）多樣性增強

• 數據樣本擾動：給定初始數據集，可從中產生出不同的數據子集，再利用不同的數據子集
  訓練出不同的個體學習器.例如：圖像中的數據增強手段
• 輸入屬性擾動：訓練樣本通常由一組屬性描述,不同的“子空間”(subspace,即屬性子集)提供了觀察數據的不同視角.顯然從不同子空間訓練出的個體學習器必然有所不同。
• 輸出表示擾動：此類做法的基本思路是對輸出表示進行操縱，以增強多樣性。可對訓練樣本的類標記稍作變動，如“翻轉法”(Flipping Output)隨機改變一些訓練樣本的標記:也可對輸出表示進行轉化,如“輸出調制法”(OutputSmearing)[Breiman,2000] 將分類輸出轉化為回歸輸出后構建個體學習器，還可將原任務拆解為多個可同時求解的子任務，如ECOC 法利用糾錯輸出碼將多分類任務拆解為一系列二分類任務來訓練基學習器
• 算法參數擾動：基學習算法一般都有參數需進行設置，例如神經網絡的隱層神經元數、初
  始連接權值等,通過隨機設置不同的參數,往往可產生差別較大的個體學習器。學習器時通常需使用交叉驗證等方法來確定參數值,這事實上已使用了不同參數訓練出多個學習器，只不過最終僅選擇其中一個學習器進行使用,而集成學習則相當于把這些學習器都利用起來; 由此也可看出集成學習技術的實際計算開銷并不比使用單一學習器大很多