【析】考慮同時取送和時間窗的車輛路徑及求解算法

期刊：computer engineering and applications 計算機工程與應用![c ](https://img-blog.csdnimg.cn/direct/eede1b868b854c6e95b51dbd8b6e0fef.png)

引言
在這里插入圖片描述

1. 問題分析

1.1 問題描述

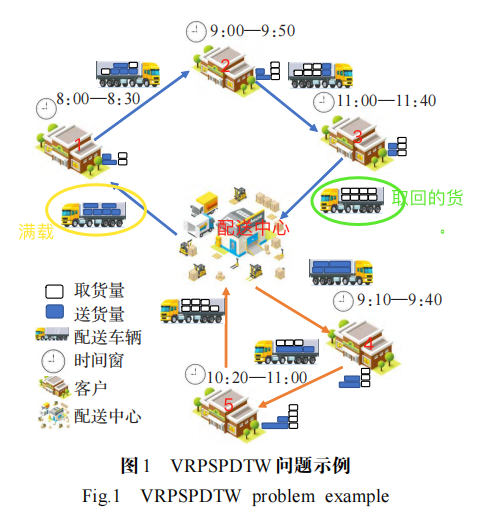
在這里插入圖片描述
問題描述為：

若干運輸車輛從配送中心出發為客戶取送貨并最終返回配送中心，每位客戶僅由一輛車服務一次，車輛在配送過程中任何時刻都不能超載。
車輛到達客戶處為客戶送貨的同時從客戶處取走回收的貨物，每位顧客具有取貨和送貨的需求。
配送中心和客戶的位置、時間窗、客戶取送貨需求量、服務時間需求，以及配送各中心和各個客戶之間的距離、車輛行駛速度均已知。
允許車輛在客戶最早開始服務時間之前到達，不允許車輛在客戶最晚開始服務時間之后到達；車輛要在配送中心最早開始時間之后為客戶服務，在配送中心最晚截止時間之間返回配送中心。

物流網絡可抽象為一連通圖：假設各節點之間相互連通；兩點之間的距離對稱，即 $d_{ij}=d_{ji}$ ;任意3個節點之間的間距滿足 $d_{ik}+d_{kj} \geq d_{ij}$ ;忽略道路、天氣及交通擁塞等其他因素。

1.2 模型建立

在這里插入圖片描述

在這里插入圖片描述

模型如下：

在這里插入圖片描述

2. 算法設計

2.1 編碼解碼與種群初始化

假設所研究的配送網絡中共有 N 個客戶，配送中心最多可使用 m 輛車，則個體的解可以表示為1~ (N + m - 1) 隨機排列。

該個體表示服務6個客戶，最多使用3輛車的一個解。配送中心表示0；客戶集 {1,2,3,4,5,6} ；車輛集 {7,8} 。
具體解碼為：

首先找到車輛節點 7、8 的位置；
提取節點 2、5、7；
在個體中刪除提取節點，在所提取節點中刪除車輛節點并在首尾加上配送中心，生成子路徑 0→2→5→0；
重復操作生成子路徑 0→3→1→0；
最后提取剩余節點生成子路徑0→4→6→0。

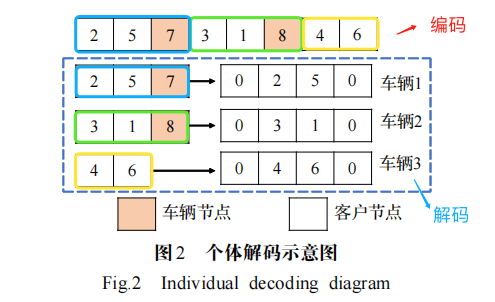
在這里插入圖片描述

編碼：(可看做基因代碼) 2,5,7,3,1,8,4,6的順序.其中 7和8是車輛節點，其他6個為客戶節點。
解碼：根據這個順序，根據車輛節點的分隔去完成配送任務。
如上所說個體解是1~8(6+3-1=8)的隨機排列。那么會有三種情況：

僅僅使用一輛車的特殊解:
7,8,1,2,4,5,3,6
1,2,4,5,3,67,8
…

使用兩輛車的解：
1,2,4,5,7,8,3,6
1,2,7,8,4,5,3,6
…

使用三兩車的解如圖2所示

還有一個問題：VRPSPDTW是在原來的VRP上擴展了同時取送和時間窗兩個約束。那么就會有一個實際的編碼解能否成立的問題？

客戶1:8:00-8:30 客戶2:9:00-9:50 客戶3:11:00-11:40
如果存在一個編碼順序 $3\to 2 \to 1$ ，則實際解碼不會成立的。

初始解的質量對算法的求解速度和求解質量影響較大。

初始解的已有的設計

，周蓉等[23]通過大部分初始種群個體隨機生成和部分優良個體采用改進節約算法的方式生成初始種群。《裝卸一體化車輛路徑問題的自適應并行遺傳算法》

以Ｃ－Ｗ節約法為基礎，設計３種基于雙重需求的啟發式種群初始化方法，并采用大部分個體隨機生成、部分優良個體采用種群初始化方法生成的方式得到初始種群。隨機產生方法遵循兩條原則：第一，不允許產生相同個體；第二，隨機產生個體與已產生個體的目標值之差應不小于某一數值Δ
Xia 等[24]采用隨機方式生成初始解，并通過設計鄰域搜索機制來降低算法對初始解的依賴性。《Improved tabu search algorithm for the open vehicle routing problem with soft time windows andsatisfaction rate》(具有軟時間窗和滿意率的開放式車輛路徑問題的改進禁忌搜索算法)
本文選擇隨機方式生成初始解，并通過對違反載重量、時間窗的懲罰機制接受不可行解，增大搜索范圍以及提高算法跳出局部最優的能力，使算法在迭代尋優中找到更優質的解。這個的意思對因為載重量、時間窗的不可行解接受，只是進行懲罰機制，以增大搜索范圍？？？

C-W節約法

C-W節約法（Clarke and Wright Saving Method）是一種經典的啟發式算法，主要用于解決車輛路徑問題（Vehicle Routing Problem, VRP）。這種方法由Clarke和Wright于1964年首次提出，目的是在車輛數不固定的情況下，為需要配送的客戶安排最經濟的路線。C-W節約法通過合并運輸路線來減少總行駛距離，從而節約成本。

C-W節約法的基本步驟如下：

初始化：從配送中心開始，為每個客戶創建一條獨立的配送路線。此時，每條路線只包含一個客戶。
計算節約量：對于每對客戶（i, j），計算如果將它們合并到同一條路線中，可以節約的行駛距離。節約量的計算公式通常為：節約量 = d(0,i) + d(0,j)
-d(i,j)，其中d(0,i)表示從配送中心到客戶i的距離，d(0,j)表示從配送中心到客戶j的距離，d(i,j)表示從客戶i到客戶j的距離。
排序：根據計算出的節約量，對所有客戶對進行降序排序。
合并路線：從節約量最大的客戶對開始，嘗試將它們合并到同一條路線中。如果合并后的路線滿足所有約束條件（如車輛載重限制、客戶時間窗等），則進行合并，并更新相關路線信息。然后，繼續考慮下一個節約量最大的客戶對。
迭代優化：重復步驟3和4，直到無法再合并任何客戶對或達到預設的迭代次數。

C-W節約法的優點在于簡單易實現，且能夠在較短的時間內得到一個較好的解。然而，它也存在一些局限性，如容易陷入局部最優解，無法保證找到全局最優解。因此，在實際應用中，通常會將C-W節約法與其他優化方法（如遺傳算法、模擬退火算法等）相結合，以提高求解質量和效率。
案例說明見：《【路徑分割】序列分隔和路徑提取的案例》

2.2 計算適應度值

解碼出的配送方案并不一定都是可行的， 首先通過式（21）、（22）分別計算當前配送方案違反載重量約束及違反時間窗約束之和，然后通過式（20）對違反載重量和時間窗約束的配送方案進行懲罰，保證算法能找到更優質的解。

在這里插入圖片描述 $G (x)$ 為當前配送方案的總成本，即目標函數；
$K (x)$ 為車輛使用數目；
$C (x)$ 為車輛總行駛距離；
$L (x)$ 為各條配送路徑違反的載重量約束之和；
$T (x)$ 為所有客戶違反的時間窗約束之和；
$β$ 為違反載重量約束的懲罰因子；
$γ$ 為違反時間窗約束的懲罰因子；
$l_i$ 為貨車到達客戶 i 的時間。

2.3 聚類及替換

（1）計算每個個體的適應度函數值，采用 k -means聚類方法把 n 個個體分成 m 個類，并將各類個體進行排序，其中最佳個體作為聚類中心。
（2）隨機產生一個 [0,1] 之間的數 r1 ，若 r1 小于給定的參數 p0（替換概率），則進入（3），否則進入生成新個體操作。
（3）在 m 個聚類中隨機選擇一個聚類的聚類中心，生成一新個體，然后用新個體替換選中的聚類中心。

猜想：在原有的遺傳算法上添加一個聚類的目的是什么呢？
根據生活經驗來看，車輛對于聚在一堆的站點跑的路程可能是短的。為了縮短優化的過程而設立的。這樣的操作對于團狀聚類會有好處的，而對于環狀聚類圖是不利的。當然，聚類的結果主要是取決于當地的地理環境的。

2.4 更新種群

更新種群的主要方法是生成新的個體，而生成新個體的方式有兩種：
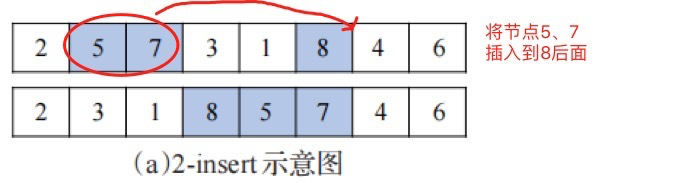
（1）選出某一個聚類中的個體進行 2-insert 和 2-opt 操作；
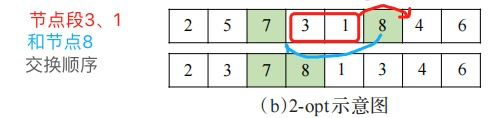
在這里插入圖片描述

（2）選出某兩個聚類中心的個體進行順序交叉操作。
順序交叉如圖3（c）所示，首先找到個體 xi 第一部分（選中的兩個客戶節點之間的部分），然后將 xj 放到 xi 第一部分之后，最后依次刪除重復個體，xj 同理。
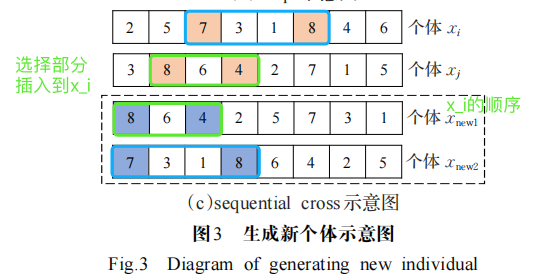
在這里插入圖片描述

這個交叉操作有點像 遺傳中的交叉操作。但不同的是，遺傳中的交叉操作是相同長度的片段交換。而這個是不同長度的。比如第一個體選中的交叉片段為7-3-1-8,長度為4；第二個個體選中的交叉片段為8-6-4,長度為3. 遺傳中的交叉操作，見博文《[基因遺傳算法]進階之四:實踐CVRP》

生成新個體的部分參數為：
$r 2 、 r 3 、 r 4 ， [0, 1]$ 之間的隨機數；
$p_1$ ，選擇一個聚類的概率；
$p_2$ ，選擇一個聚類中聚類中心的概率；
$p_3$ ，選擇兩個聚類中聚類中心的概率；
$C_i(i = 1,2,?,m)$ ，第 i 個聚類的聚類中心；
$x_1$ ，從聚類中選出的第一個個體；
$x_2$ ，從聚類中選出的第二個個體；
$obj(x_i ) (i = 1,2,?,n)$ ，個體 xi 的目標函數值。

假設種群（population）數目為 n ，聚類數目為 m(m > 2) ，
更新種群的偽代碼如下所示。

2.5 局部搜索策略

本文的目標函數成本主要與行駛距離、時間窗、車輛指派數相關，而車輛指派數又與取送貨需求量相關，因此本文設計的大鄰域搜索算子主要與上述四點相關，破壞操作結束后輸出被移除的節點集合 R ，以及被破壞的個體 $S_{destory}$ ；修復操作結束后輸出修復后的個體 $S_{repair}$ 。本文共設計了6種“破壞”與“修復”算子。

2.5.1 破壞算子

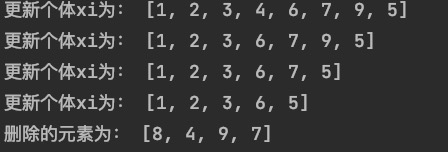
（1）路徑隨機破壞：隨機選擇種群中一個個體 $x_i$ ，然后再隨機選擇一個節點放入被移除的節點集合 $R$ ，同時更新 $x_i$ ，重復操作，直到 $r$ 個節點被移除。

python舉例：講解一個簡單的破壞算子

import numpy as np
Populations=[[1,2,3,4,5,6,7,8,9],[1,2,3,5,6,9,4,7,8],[1,2,3,4,6,7,5,8,9],[1,2,3,4,6,8,7,9,5],[1,2,3,5,7,9,4,6,8],[1,2,3,7,5,4,8,6,9] ]
#是某個種群,個數為6
## 一、路徑隨機破壞
xi=Populations[np.random.randint(low=0, high=6)] #隨機選擇一個個體
R=[] #被移除的節點集合
r = 4 #假設重復4次移除操作
for i in range(r):index=np.random.randint(10-r) #移除前的序列長度，隨機選擇一個下標R.append(xi.pop(index)) #將刪除的元素放入結合R中print("更新個體xi為：",xi)
print("刪除的元素為：",R)

運行結果展示：
在這里插入圖片描述

（2）相似度破壞：該算子分別從行駛距離、時間窗、送取貨需求量，以及是否同一路徑四方面考慮兩個節點的相似度。兩節點間的相似度由 R(i,j) 表示，其表達式如下：
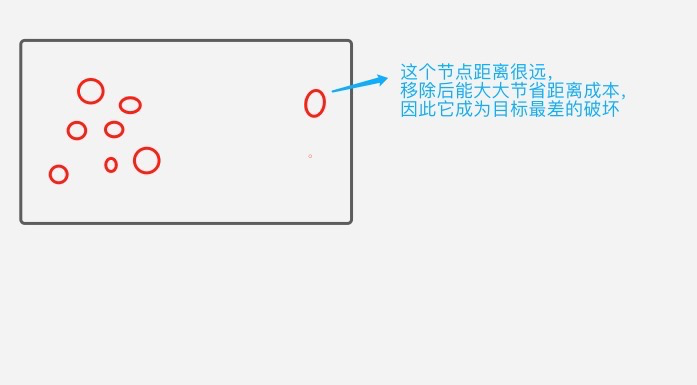
在這里插入圖片描述
（3）目標最差破壞：該算子主要目標是移除對目標成本影響最大的節點，包括考慮距離、時間窗兩方面，從而直觀地改善總的運輸成本。

猜測的情況如下：

2.5.2 修復算子

（1）貪婪修復算子：在滿足所有約束的基礎上從被移除的節點集合 R 中隨機選擇一個節點，找到該節點可插入的位置，計算該點插入某一位置后的插入成本（將 R 中的某個節點插入 $S_{destory}$ 的某個位置后，此時修復后的總成本減去修復前的總成本即為 “插入成本” ），選擇 插入成本增加最少的位置進行插入，重復操作直到R 為空集。

（2）遺憾值修復：在滿足約束的基礎上，R 中節點 i在 $S_{destory }$ 若有 $l$ 個可插入位置，則對應產生 $l$ 個插入成本。將 $l$ 個插入成本從小到大排序，排在第二位的插入成本減去排在第一位的插入成本即為節點 i 插回 $S_{destory}$ 的遺憾值。

xi=[1,2,3,6,5] ,原成本 $10$ , R=[8,4,9,7]
對于節點8滿足約束的基礎上有 $l = 6$ 個插入位置(所有的位置都可以插入),則產生 $l = 6$ 個結果。

[8,1,2,3,6,5], 修復后成本11,插入成本 $c 1 = 1$
[1,8,2,3,6,5], 修復后成本16,插入成本 $c 2 = 6$
[1,2,8,3,6,5], 修復后成本14,插入成本 $c 3 = 4$
[1,2,3,8,6,5], 修復后成本18,插入成本 $c 4 = 8$
[1,2,3,6,8,5], 修復后成本15,插入成本 $c 5 = 5$
[1,2,3,6,5,8], 修復后成本13,插入成本 $c 6 = 3$

對于貪婪修復算子會選擇插入成本最小的第一種插法。
計算遺憾值：
排序： $\to c6(3)\to c3(4) \to c4(5) \to c2(6) \to c4(8)$
遺憾值為 3-1=2

（3）最短距離修復：在滿足約束的基礎上從 R 中隨機選擇一個節點 k ，計算 k 各個插入位置的節約值，如將節點 k 插入節點 i、j 之間，則節約值 Δd(i,k,j) = dik +dkj - dij 。選擇節約值最小的位置進行插入并更新 R ，重復操作直到 R 為空集。

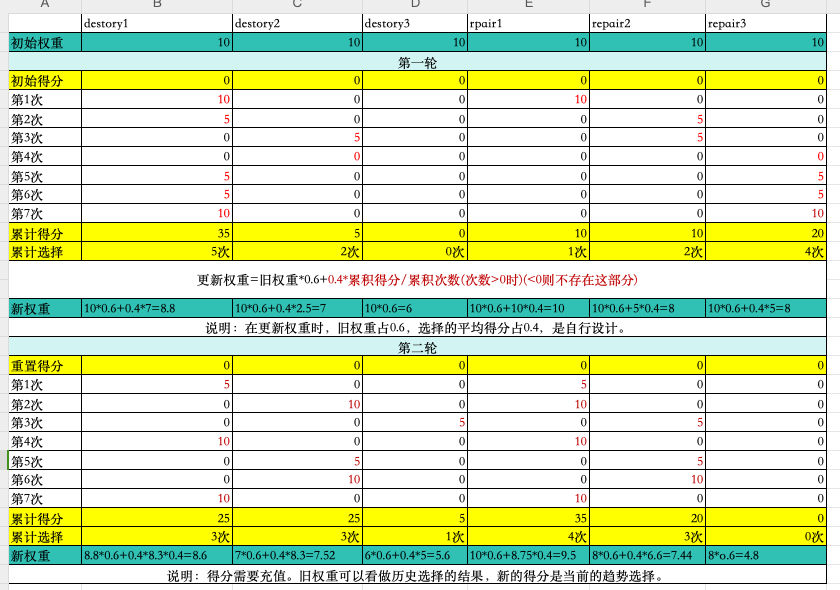
2.6 自適應機制

為增強算法的自適應調整能力，本文 為每種破壞和修復算子分配了權重 λ 。基于賭輪盤的思想，在迭代過程中，根據每種算子被分配的權重在所有算子權重中所占的比例 ωi ，首先自適應選擇其中一種破壞算子對當前個體 x 進行破壞，然后同樣以自適應的方式選擇修復算子進行修復操作。每種算子權重占比 ωi 計算公式為：

在這里插入圖片描述
破壞、修復、記錄的過程

在解搜索前，選擇破壞和修復算子,并記錄
destory_id,repair_id=selectDestoryRepair(model)
model.d_select[destory_id]+=1 model.r_select[repair_id]+=1
執行破壞算子，獲得移除的節點集合
reomve_list=doDestory(destory_id,model,sol)這里的sol是鄰域搜索的出發解。
執行修復算子，獲得新的解
new_sol=doRepair(repair_id,reomve_list,model,sol)
比較新解、最優解、出發解，根據得分規則得分。

將最優解放入歷史最優解中
history_best_obj.append(model.best_sol.obj)

在上面的過程中，值得解說的有以下幾點：

破壞和修復算子的選擇是沒有關聯的。所有共有3*3=9中選擇(本文中設置了3種破壞3中修復)。但可成對選擇的。
每一輪破壞和修復都會有一個得分，然后對應到破算算子和修復算子的位置記錄。然后這個得分又會影響算子的選擇。
得分和權重的影響如下：

2.7 迭代終止條件

ABSO有兩種迭代的終止條件，只要滿足條件之一便使算法終止迭代：
（1）當種群中的最優解連續不變的迭代次數達到預設的閾值 $max_{remain}$ ；
（2）當實際總迭代次數達到預設的最大迭代次數 $max_{gen}$
終止迭代后，選取全局最優解作為最終解輸出。

2.8 ABSO算法流程

ABSO 算法1??引入 ALNS 算法局部搜索機制，進行有效的鄰域搜索，并2??通過懲罰機制在一定情況下接受不可行解，加深種群搜索，3??通過聚類及替換操作增加種群的多樣性，避免算法陷入局部最優，以更大幾率找到優質解，算法具體流程如下所示。

輸入：算法參數、客戶信息、車輛信息、迭代次數等。
輸出：VRPSPDTW問題車輛配送方案。

提取數據信息，初始化算法參數
種群初始化：生成初始種群
初始化全局最優，保留每次迭代全局最優
開始迭代循環

在4.循環中，藍框部分是優化種群的過程。
有點類似于遺傳算法，只是把交叉、變異改成了藍框部分。

3 算例實驗與分析

為驗證模型和算法的有效性，本文進行 3 組實驗。實驗1驗證本文算法在小規模標準算例方面的有效性，分別對 10、25、50個客戶數量的小規模標準算例進行實驗。實驗2驗證本文算法對大規模標準算例的性能，針對6組不同類型大規模標準算例，每組隨機抽選3個，共選取18個算例進行實驗，每個算例包含100個客戶。實驗3引入具體問題案例對算法性能進行測試，驗證算法實際應用價值。

本文算法由 Matlab- 2018a 編程實現，在 CPU 為
AMD Ryzen 5 2500U，2.00 GHz，內存為 8.00 GB 的
Windows10 操作系統的計算機上運行。算法參數設置
如下：

最大迭代次數 Maxgen = 400 ；
種群規模 Popsize =50~100 ，種群的規模與客戶點規模 n 有關，n 越小種群規模越小。
考慮測試算例車輛數目，選取聚類數目為 8個；
p_replace 調整算法局部與全局的關系，將該參數設置為0.3；
參數 p_one 與算法搜索鄰域大小成反比，將該參數設置為 0.4；
p_one_center 、p_two_center 主要考慮局部最優與隨機個體的關系，為防止陷入局部最優并且加大算法搜索效率，將上述參數分別設置為0.3、0.2。

算法參數根據控制變量法實驗得出，每次調整只變動某一個參數進行反復實驗，確定了合適的參數值，具體參數設置如表1所示。

在這里插入圖片描述

3.1 小規模標準算例分析

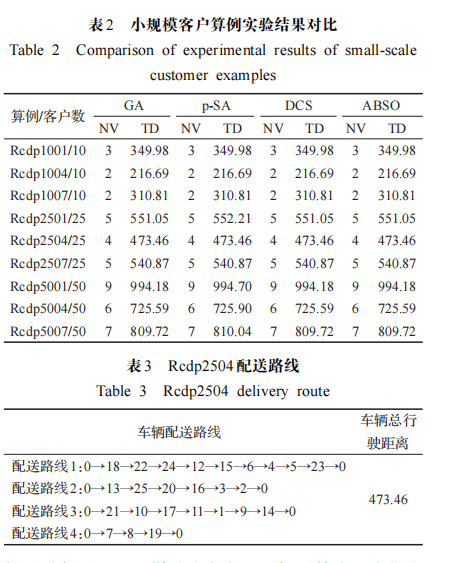
實驗 1 采用文獻[8]的 9 個小規模標準算例進行實驗，9個小規模標準算例包括3個10個客戶規模，3個25個客戶規模，3個50個客戶規模。將實驗結果與文獻[8]（GA）算法、文獻[9]（p-SA）算法和文獻[10]（DCS）算法對比，所對比文獻的??主要目標函數均為最小化車輛使用數（number vehicle，NV），??次要目標函數為最小化行駛距離（travel distance，TD），本文也采用相同的目標函數。

實驗對比結果如表2所示，表3給出了算例Rcdp2504的車輛配送路線。不難看出，本文設計的算法可以全部求得小規模標準算例已知的最優解，驗證了本文算法對VRPSPDTW小規模標準算例求解的有效性。

在這里插入圖片描述

3.2 大規模標準算例分析

實驗2 為驗證本文算法對大規模算例的有效性，選用文獻[8]設計的大規模標準算例進行實驗。為保證實驗的準確性，針對6組實驗數據，隨機選擇每組的3個算例進行實驗，每個算例包含 100個客戶。在同時滿足載重量和時間窗約束的條件下進行實驗，將實驗結果與文獻[8]（GA）算法、文獻[9]（p-SA）算法和文獻[10]（DCS）算法算法進行對比。同樣的本文主要目標函數為最小化車輛使用數（NV），次要目標函數為最小化行駛距離（TD）。
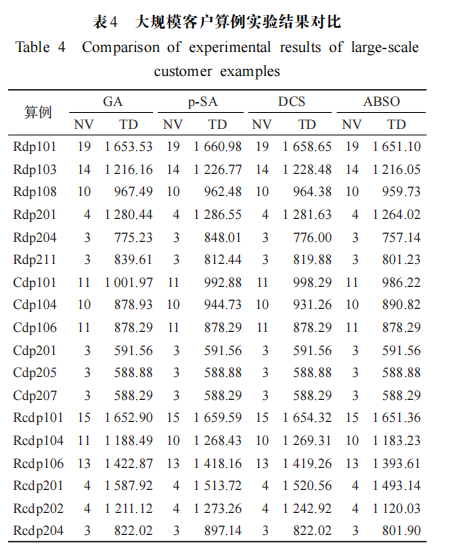
在這里插入圖片描述

實驗對比結果如表 4所示。可以看出，在🐸求解質量方面，本文提出的算法在隨機選擇的 18 個標準算例中有13個算例更新了最優解，4個算例取得與當前最優解相同的結果。其中算例Rcdp202與GA算法相比提升了7.52%，與 p- SA、DCS 算法相比分別提升了 12.03%、9.89%。🐸在求解速度方面，如圖4所示，本文算法可以在較少的迭代次數內快速收斂，當算法陷入局部最優解時，可快速跳出局部最優，具有較好的尋優性能。 為更直觀地展示本文實驗結果，圖 5給出了算例 Rcdp106的配送路線圖。綜合隨機選取的 18 個標準算例實驗數據，本文算法更新或達到最優的算例占測試算例的94.45%，其中 72.22%的算例更新了最優解，充分說明了本文提出的模型和算法在解決大規模標準算例方面的有效性。
在這里插入圖片描述

3.3 應用案例分析

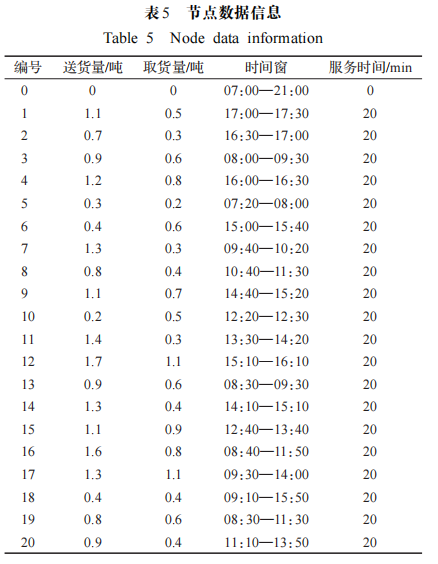
實驗 3 為驗證本文算法在實際物流案例中的有效性，本文獲取了某物流快遞公司在一定區域內的數據信息，包括1個中轉物流中心，20個門店的送貨量、取貨量以及服務時間要求。為進一步提高算法的可靠性及實際案例的應用價值，本文在考慮道路通暢信息的情況下導出配送中心與各個門店之間距離矩陣。此外，通過實地調研的方式獲取各個門店的取送貨量需求以及服務時間需求，保證數據的準確性。為計算方便，對中轉配送中心和各個門店進行編號，其中0表示中轉配送中心節點，1~20表示20個門店節點，具體數據如表5所示。

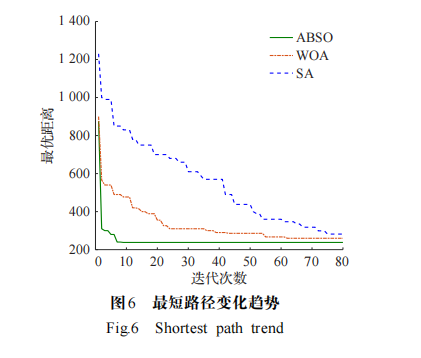
在這里插入圖片描述

仿真實驗開始前首先計算中轉中心及各個門店考慮道路通暢的距離矩陣，然后將客戶的時間窗約束轉換為具體數值，繼而程序開始讀取各個門店的數據信息，進行迭代運算。同樣的，本實驗的主要目標函數為最小化車輛使用數（NV），次要目標函數為最小化行駛距離（TD），算法最短路徑變化趨勢曲線如圖 6 所示，圖 7 給出了車輛配送路線。與模擬退火算法（SA）、鯨魚優化算法（WOA）進行對比，結果表明，在尋優能力方面，本文求解最優解為 237.85，與 SA 算法（282.64）、WOA 算法（261.42）相比分別有 18.83%和 9.91%的優化；在收斂速度方面，本文算法能夠在較短的迭代次數尋得優質解，且不易陷入局部最優。充分表明了本文算法在解決實際VRPSPRTW物流運輸問題時的可行性和實際應用價值。
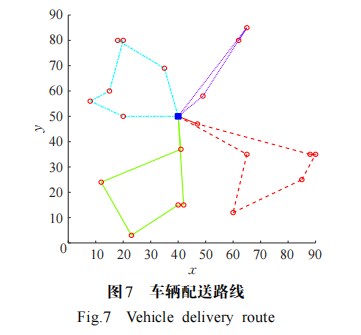
在這里插入圖片描述

4 結束語

VRPSPDTW 是一類應用廣泛的復雜車輛路徑問題，因其問題的特殊性、復雜性和諸多限制條件等特征，需要高性能的求解算法。本文針對該問題，構建了基于車輛使用成本和車輛行駛距離成本總成本最少的路徑優化模型，提出自適應頭腦風暴算法（ABSO）求解。ABSO 具有如下優點：
采用新的編解碼方式，并對不滿足約束條件的個體進行多項懲罰，擴大全局搜索區域；
使用聚類操作和三種不同的路徑搜索策略來推動算法較快地到達優質解空間；
以六種破壞-修復算子備選集合為依據，通過自適應動態選擇鄰域搜索機制對優質解空間進行局部搜索，有效平衡了搜索廣度與搜索深度之間的關系，從而提升算法性能。

對不同規模測試算例和算法進行比較，ABSO在小規模客戶標準算例和大規模客戶標準算例以及實際物流案例中，均能以較快的收斂速度找到近似最優解，且尋優性能好于所對比算法，充分驗證了本文算法的有效性。
本文研究的VRPSPDTW 問題是需求不可拆分的問題，即每個客戶只能由一輛車服務一次，后續研究方向是松弛每個客戶只能由一輛車服務一次的約束，考慮需求拆分對VRPSPDTW產生的影響以及相對應的算法設計。