導包

import numpy as npimport matplotlib.pyplot as plt
%matplotlib inlinefrom sklearn.linear_model import LinearRegression

創建數據

X = np.linspace(2,10,20).reshape(-1,1)# f(x) = wx + b
y = np.random.randint(1,6,size = 1)*X + np.random.randint(-5,5,size = 1)# 噪聲，加鹽
y += np.random.randn(20,1)*0.8plt.scatter(X,y,color =  'red')

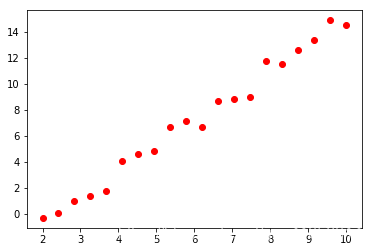
使用已有的線性回歸擬合函數

lr = LinearRegression()
lr.fit(X,y)w = lr.coef_[0,0]
b = lr.intercept_[0]
print(w,b)plt.scatter(X,y)x = np.linspace(1,11,50)plt.plot(x,w*x + b,color = 'green')

1.965481199093173 -4.644495936205775

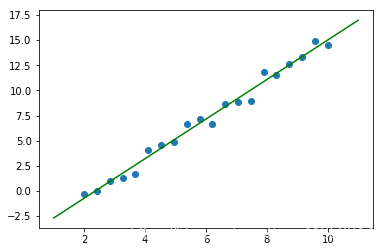
自己實現了線性回歸（簡版）

# 使用梯度下降解決一元一次的線性問題：w，b
class LinearModel(object):def __init__(self):self.w = np.random.randn(1)[0]self.b = np.random.randn(1)[0]
#     數學建模：將數據X和目標值關系用數學公式表達def model(self,x):#model 模型，f(x) = wx + breturn self.w*x + self.bdef loss(self,x,y):#最小二乘得到缺失值cost = (y - self.model(x))**2
#         梯度就是偏導數，求解兩個未知數：w，bgradient_w = 2*(y - self.model(x))*(-x)gradient_b = 2*(y - self.model(x))*(-1)return cost,gradient_w,gradient_b
#     梯度下降def gradient_descent(self,gradient_w,gradient_b,learning_rate = 0.1):
#         更新w，bself.w -= gradient_w*learning_rateself.b -= gradient_b*learning_rate
#     訓練fitdef fit(self,X,y):count = 0 #算法執行優化了3000次，退出tol = 0.0001last_w = self.w + 0.1last_b = self.b + 0.1length = len(X)while True:if count > 3000:#執行的次數到了break
#           求解的斜率和截距的精確度達到要求if (abs(last_w - self.w) < tol) and (abs(last_b - self.b) < tol):breakcost = 0gradient_w = 0gradient_b = 0for i in range(length):cost_,gradient_w_,gradient_b_ = self.loss(X[i,0],y[i,0])cost += cost_/lengthgradient_w += gradient_w_/lengthgradient_b += gradient_b_/length
#             print('---------------------執行次數：%d。損失值是：%0.2f'%(count,cost))last_w = self.wlast_b = self.b# 更新截距和斜率self.gradient_descent(gradient_w,gradient_b,0.01)count+=1def result(self):return self.w,self.b

取值的時候X 是二維的所以 取出X，y數據中的第一個數

self.loss(X[i,0],y[i,0])

使用自己實現的線性回歸擬合函數

lm = LinearModel()lm.fit(X,y)w_,b_ = lm.result()plt.scatter(X,y,c = 'red')plt.plot(x,1.9649*x - 4.64088,color = 'green')plt.plot(x,w*x + b,color = 'blue')plt.title('自定義的算法擬合曲線',fontproperties = 'KaiTi')

Text(0.5, 1.0, ‘自定義的算法擬合曲線’)

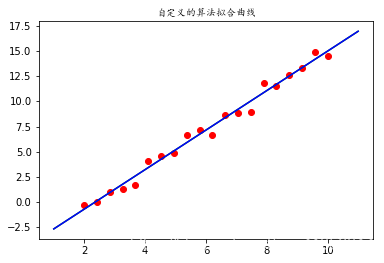
多元的線性回歸

import numpy as npimport matplotlib.pyplot as plt
%matplotlib inlinefrom sklearn.linear_model import LinearRegression

其實相似

# 一元二次
# f(x) = w1*x**2 + w2*x + b# 二元一次
# f(x1,x2) = w1*x1 + w2*x2 + bX = np.linspace(0,10,num = 500).reshape(-1,1)X = np.concatenate([X**2,X],axis = 1)
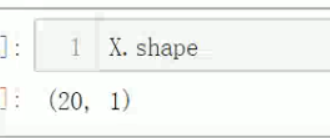
X.shape

(500, 2)

w = np.random.randint(1,10,size = 2)
b = np.random.randint(-5,5,size = 1)
# 矩陣乘法
y = X.dot(w) + b
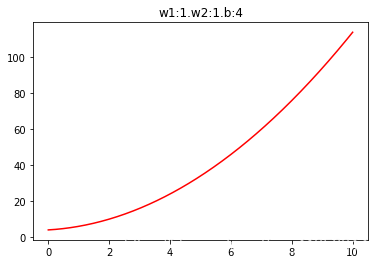
plt.plot(X[:,1],y,color = 'r')plt.title('w1:%d.w2:%d.b:%d'%(w[0],w[1],b[0]))

Text(0.5, 1.0, ‘w1:1.w2:1.b:4’)

使用sklearn自帶的算法，預測

lr = LinearRegression()lr.fit(X,y)print(lr.coef_,lr.intercept_)plt.scatter(X[:,1],y,marker = '*')x = np.linspace(-2,12,100)plt.plot(x,1*x**2 + 6*x + 1,color = 'green')

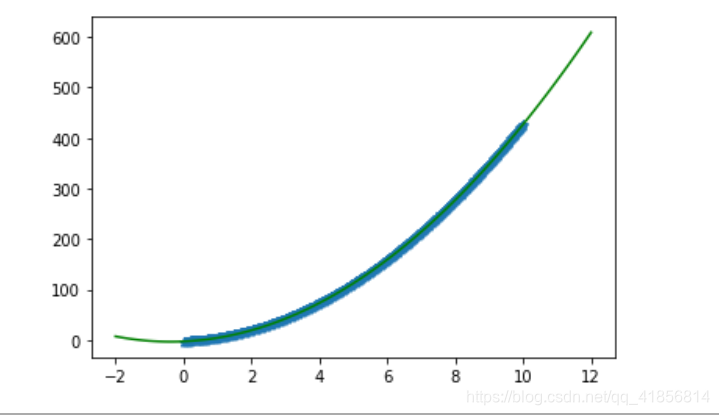
[1. 1.] 3.999999999999993

自己手寫的線性回歸，擬合多屬性，多元方程

# epoch 訓練的次數，梯度下降訓練多少
def gradient_descent(X,y,lr,epoch,w,b):
#     一批量多少，長度batch = len(X)for i in range(epoch):
#         d_loss:是損失的梯度d_loss = 0
#         梯度，斜率梯度dw = [0 for _ in range(len(w))]
#        截距梯度db = 0for j in range(batch):y_ = 0 #預測的值 預測方程 y_ = f(x) = w1*x1 + w2*x2 + b#求預測值y_，分開了 先*w 再加bfor n in range(len(w)):y_ += X[j][n]*w[n]y_ += b#再利用最小二乘法 求導 得出損失值 再求導得到梯度 d_loss #再將梯度求導 y_ = f(x) = w1*x1 + w2*x2 + b 來對w1求導結果為就為 X[j][n] 再乘 d_loss 求dw的值 可能有點亂。#db 一樣 根據b來對y_ 求導得1
#            平方中求導兩種情況相同 ，
#             (y - y_)**2 -----> 2*(y-y_)*(-1)
#             (y_- y)**2  -----> 2*(y_ - y)*(1)d_loss = -(y[j] - y_)#再求w的梯度  就是對y[j]求導 這個系數2 不影響結果#結果為 w1' =  X[j][n]*d_loss#cost = (y - (w1*X[j][0] + w2*X[j][1] +…… + b)**2          #w1梯度，導數# -2*（y - y_） * X[j][0]for n in range(len(w)):dw[n] += X[j][n]*d_loss/float(batch)db += 1*d_loss/float(batch)
#         更新一下系數和截距，梯度下降for n in range(len(w)):w[n] -= dw[n]*lr[n]b -= db*lr[0]return w,b

lr = [0.0001,0.0001]
w = np.random.randn(2)
b = np.random.randn(1)[0]
w_,b_ = gradient_descent(X,y,lr,5000,w,b)
print(w_,b_)

[1.00325157 1.22027686] 2.1550745865631895

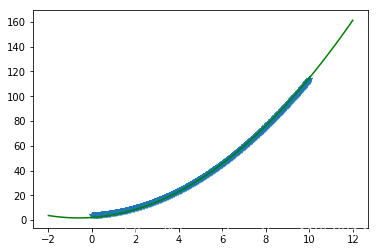
plt.scatter(X[:,1],y,marker = '*')x = np.linspace(-2,12,100)f = lambda x:w_[0]*x**2 + w_[1]*x + b_plt.plot(x,f(x),color = 'green')